12.1: Una descripción clásica de la espectroscopia

El tratamiento mecánico cuántico tradicional de la espectroscopia es una representación estática de un proceso muy dinámico. Un campo de luz oscilante actúa para impulsar cargas ligadas en la materia, lo que bajo condiciones de resonancia conduce a un intercambio eficiente de energía entre la luz y la materia. Esta imagen dinámica surge de una descripción en el dominio del tiempo, que comparte muchas similitudes con una descripción clásica. Dado que gran parte de la intuición física que es útil para comprender la espectroscopia emerge naturalmente de la visión clásica, la describiremos primero.

La visión clásica comienza con la observación de que los átomos y moléculas están compuestos por partículas cargadas, y estas cargas son el mango por el cual un campo electromagnético ejerce una fuerza sobre el átomo o molécula. La fuerza ejercida sobre las moléculas depende de la forma del potencial que une las cargas, la magnitud de las cargas y la fuerza del campo externo.

Los elementos más simples de un modelo que captura lo que sucede en la espectroscopia de absorción requieren que consideremos una partícula cargada en un potencial ligado que interactúa con una fuerza impulsora oscilante. La materia puede expresarse en términos de una partícula con carga\(z\) en un potencial armónico (el término principal en cualquier expansión del potencial en la coordenada\(Q\)):

\[V _ {r e s} (t) = \dfrac {1} {2} \kappa Q^{2} \label{11.1}\]

Aquí\(k\) está la constante de la fuerza restauradora. Para el campo de luz, utilizamos la expresión tradicional

\[V _ {e x t} (t) = - \overline {\mu} \cdot \overline {E} (t) \label{11.2}\]

para un campo electromagnético externo que interactúa con el momento dipolar del sistema,\(\overline {\mu} = z Q\). Describimos el comportamiento de este sistema usando la ecuación de movimiento de Newton F=Ma, la cual escribimos como

\[m \dfrac {\partial^{2} Q} {\partial t^{2}} = F _ {r e s} + F _ {d a m p} + F _ {e x t} \label{11.3}\]

En el lado derecho de la Ecuación\ ref {11.3} hay tres fuerzas: la fuerza restauradora armónica, una fuerza de amortiguación y la fuerza impulsora ejercida por la luz. Recordando que

\[F = - ( \partial V / \partial Q )\]

podemos escribir la Ecuación\ ref {11.3} como

\[m \dfrac {\partial^{2} Q} {\partial t^{2}} = - \kappa Q - b \dfrac {\partial Q} {\partial t} + F _ {0} \cos ( \omega t ) \label{11.4}\]

Aquí,\(b\) describe la tasa de amortiguación. Para el campo, solo hemos considerado la dependencia del tiempo

\[\overline {E} (t) = \overline {E} _ {0} \cos ( \omega t )\]

y la amplitud de la fuerza motriz

\[F _ {0} = \left( \dfrac {\partial \overline {\mu}} {\partial Q} \right) \cdot \overline {E} _ {0} \label{11.5}\]

La ecuación\ ref {11.5} indica que aumentar la fuerza sobre el oscilador se logra elevando la magnitud del campo, aumentando cuánto se desplaza la carga, o mejorando la alineación entre la polarización del campo eléctrico y el momento dipolar de transición. Podemos reescribir la ecuación\ ref {11.4} como la ecuación del oscilador armónico impulsado:

\[\dfrac {\partial^{2} Q} {\partial t^{2}} + 2 \gamma \dfrac {\partial Q} {\partial t} + \omega _ {0}^{2} Q = \dfrac {F _ {0}} {m} \cos ( \omega t ) \label{11.6}\]

Aquí la constante de amortiguación\(\gamma = b / 2 m\) y la frecuencia de resonancia armónica\(\omega _ {0} = \sqrt {\kappa / m}\).

Veamos la solución a la Ecuación\ ref {11.6} para un par de casos simples.

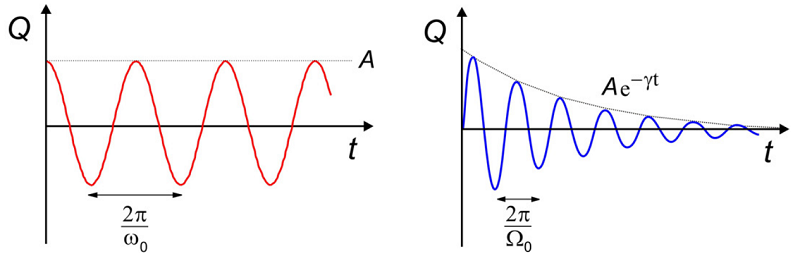
Primero, para el caso (curva roja) de que no hay amortiguación o fuerza motriz (\(\gamma = F _ {0} = 0\)), tenemos soluciones armónicas simples en las que oscilan a una frecuencia\(\omega _ {0}\):

\[Q (t) = A \sin \left( \omega _ {0} t \right) + B \cos \left( \omega _ {0} t \right)\]

Sólo quedemos con el\(sin\) término por ahora. Ahora bien, si le agregas amortiguación a la ecuación:

\[Q (t) = A e^{- \gamma t} \sin \Omega _ {0} t\]

La coordenada oscila a una frecuencia reducida

\[\Omega _ {0} = \sqrt {\omega _ {0}^{2} - \gamma^{2}}\]

A medida que continuamos, supongamos un caso con amortiguación débil para el cual\(\Omega _ {0} \approx \omega _ {0}\) (curva azul).

La solución a la Ecuación\ ref {11.6} toma la forma

\[Q (t) = \dfrac {F _ {0} / m} {\sqrt {\left( \omega _ {0}^{2} - \omega^{2} \right)^{2} + 4 \gamma^{2} \omega^{2}}} \sin ( \omega t + \beta ) \label{11.7}\]

donde el factor de fase es

\[\tan \beta = \left( \omega _ {0}^{2} - \omega^{2} \right) / 2 \gamma \omega \label{11.8}\]

Entonces esta solución al desplazamiento de la partícula dice que la amplitud ciertamente depende de la magnitud de la fuerza impulsora, pero lo más importante de la condición de resonancia. La frecuencia del campo de conducción debe coincidir con la frecuencia de resonancia natural del sistema,\(\omega _ {0} \approx \infty\)... como empujar a alguien en un columpio. Cuando conduces el sistema a la frecuencia de resonancia habrá una transferencia eficiente de potencia al oscilador, pero si empujas con frecuencia arbitraria, no pasará nada. En efecto, eso es lo que es un espectro de absorción: una medida de la potencia absorbida por el sistema desde el campo.

Observe que la coordenada oscila a la frecuencia de conducción ω y no a la frecuencia de resonancia\(\omega_0\). Además, la partícula oscila como un pecado, es decir, 90° fuera de fase con el campo cuando se acciona en resonancia. Esto refleja el hecho de que la fuerza máxima se puede ejercer sobre la partícula cuando está estacionaria en los puntos de inflexión. El desplazamiento de fase\(\beta\), depende varía con la desintonización de la resonancia. Ahora podemos hacer algunas simplificaciones a la Ecuación\ ref {11.7} y calcular el espectro de absorción. Para amortiguamiento débil\(\gamma < < \omega _ {0}\) y resonancia cercana\(\omega _ {0} \approx \infty\), podemos escribir

\[\left( \omega _ {0}^{2} - \omega^{2} \right)^{2} = \left( \omega _ {0} - \omega \right)^{2} \left( \omega _ {0} + \omega \right)^{2} \approx 4 \omega _ {0}^{2} \left( \omega _ {0} - \omega \right)^{2} \label{11.9}\]

El espectro de absorción es una medida de la potencia transferida al oscilador, por lo que podemos calcularlo encontrando la potencia absorbida por la fuerza sobre el oscilador multiplicada por la velocidad, promediada a lo largo de un ciclo del campo.

\[ \begin{align} P _ {a v g} &= \left\langle F (t) \cdot \dfrac {\partial Q} {\partial t} \right\rangle _ {a v g} \\[4pt] &= \dfrac {\gamma F _ {0}^{2}} {2 m} \dfrac {1} {\left( \omega - \omega _ {0} \right)^{2} + \gamma^{2}} \label{11.10} \end{align}\]

Esta es la forma de línea Lorentziana, que alcanza su punto máximo en la frecuencia de resonancia y tiene un ancho de línea de\(2\gamma\) (ancho completo medio máximo, FWHM). El área bajo el lineshape es\(\pi F _ {0}^{2} / 4 m\).