12.2: Descripción de la función de correlación de tiempo de la forma de línea de absorción

La interacción de la luz y la materia, tal como hemos descrito a partir de la Regla de Oro de Fermi, da las tasas de transición entre estados propios discretos del material hamiltoniano\(H_0\). La dependencia de la frecuencia a la tasa de transición es proporcional a un espectro de absorción. También sabemos que la interacción con el campo de luz prepara una superposición de los autoestados de\(H_0\), y esto conduce a la oscilación periódica de amplitud entre los estados. Sin embargo, la expresión de la tasa de transición realmente parece ocultar cualquier descripción dependiente del tiempo de los movimientos en el sistema. Un enfoque alternativo a la espectroscopia es reconocer que las características en un espectro son solo una representación en el dominio de la frecuencia de la dinámica molecular subyacente de las moléculas. Para la absorción, el espectro codifica los cambios dependientes del tiempo del momento dipolar molecular para el sistema, que a su vez depende de la posición de los electrones y núcleos.

Se puede usar una función de correlación de tiempo para el operador dipolo para describir la dinámica de un conjunto de equilibrio que dicta un espectro de absorción. Haremos uso de las expresiones de velocidad de transición de la teoría de perturbación de primer orden que derivamos en la sección anterior para expresar la absorción de radiación por dipolos como función de correlación en el operador dipolo. Comencemos con la tasa de absorción y emisión estimulada entre un estado inicial\(| \ell \rangle\) y un estado final\(| k \rangle\) inducidos por un campo monocromático

\[w _ {k \ell} = \dfrac {\pi E _ {0}^{2}} {2 \hbar^{2}} | \langle k | \hat {\varepsilon} \cdot \overline {\mu} | \ell \rangle |^{2} \left[ \delta \left( \omega _ {k \ell} - \omega \right) + \delta \left( \omega _ {k \ell} + \omega \right) \right] \label{11.11}\]

Para taquigrafía hemos escrito

\[\left| \overline {\mu} _ {k \ell} \right|^{2} = | \langle k | \hat {\mathcal {E}} \cdot \overline {\mu} | \ell \rangle |^{2}.\]

Nos gustaría usar esto para calcular el coeficiente de absorción observable experimentalmente (sección transversal) que describe la transmisión a través de la muestra

\[T = \exp [ - \Delta N \alpha ( \omega ) L ] \label{11.12}\]

La sección transversal de absorción describe la tasa de absorción de energía por unidad de tiempo en relación con la intensidad de la luz incidente en la muestra

\[\alpha = \dfrac {- \dot {E} _ {r a d}} {I} \label{11.13}\]

La intensidad del incidente es

\[I = \frac {c} {8 \pi} E _ {0}^{2} \label{11.14}\]

Si tenemos dos estados discretos\(| m \rangle\) y\(| n \rangle\) con\(E _ {m} > E _ {n}\), la tasa de absorción de energía es proporcional a la tasa de absorción y la energía de transición

\[- \dot {E} _ {r a d} = w _ {n n} \cdot \hbar \omega _ {n m} \label{11.15}\]

Para un conjunto esta tasa debe ser escalada por la probabilidad de ocupar el estado inicial.

De manera más general, queremos considerar la tasa de pérdida de energía del campo como resultado de la diferencia en las tasas de absorción y emisión estimulada entre estados poblados con una distribución térmica.

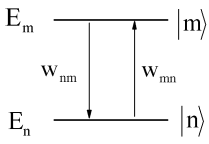
Entonces, sumando todos los estados iniciales y finales posibles\(| \ell \rangle\) y\(| k \rangle\) sobre todos los estados superiores e inferiores posibles\(| m \rangle\) y\(| n \rangle\) con

\[\left.\begin{aligned} - \dot {E} _ {\text {rad}} & = \sum _ {\ell , k \in [ m , n \}} p _ {\ell} w _ {k \ell} \hbar \omega _ {k \ell} \\ & = \dfrac {\pi E _ {0}^{2}} {2 \hbar} \sum _ {\ell , k \in [ m , n \}} \omega _ {k \ell} p _ {\ell} \left| \overline {\mu} _ {k \ell} \right|^{2} \left[ \delta \left( \omega _ {k \ell} - \omega \right) + \delta \left( \omega _ {k \ell} + \omega \right) \right] \end{aligned} \right. \label{11.16}\]

La sección transversal que incluye el cambio neto en la energía como resultado de la absorción\(| n \rangle \rightarrow | m \rangle\) y la emisión estimulada\(| m \rangle \rightarrow | n \rangle\) es:

\[\alpha ( \omega ) = \dfrac {4 \pi^{2}} {\hbar c} \sum _ {n , m} \left[ \omega _ {m n} p _ {n} \left| \overline {\mu} _ {m n} \right|^{2} \delta \left( \omega _ {m n} - \omega \right) + \omega _ {n m} p _ {m} \left| \overline {\mu} _ {n m} \right|^{2} \delta \left( \omega _ {n m} + \omega \right) \right] \label{11.17}\]

Para simplificar la Ecuación\ ref {11.17}, observamos:

1. Desde\(\delta (x) = \delta ( - x )\) entonces\[\delta \left( \omega _ {n n} + \omega \right) = \delta \left( - \omega _ {m n} + \omega \right) = \delta \left( \omega _ {m n} - \omega \right).\]
2. Los elementos de la matriz al cuadrado en los dos términos de la Ecuación\ ref {11.17} son los mismos:\[\left| \overline {\mu} _ {m n} \right|^{2} = \left| \overline {\mu} _ {n m} \right|^{2}.\]
3. y como resultado de la función delta que hace cumplir esta igualdad:\[\omega _ {m n} = - \omega _ {n m} = \omega\]

Entonces,

\[\alpha ( \omega ) = \dfrac {4 \pi^{2} \omega} {\hbar c} \sum _ {n , m} \left( p _ {n} - p _ {m} \right) \left| \overline {\mu} _ {m n} \right|^{2} \delta \left( \omega _ {m n} - \omega \right) \label{11.18}\]

Aquí vemos que el coeficiente de absorción depende de la diferencia poblacional entre los dos estados. Esto se espera ya que la absorción conducirá a la pérdida de intensidad, mientras que la emisión estimulada conduce a la ganancia. Con poblaciones iguales en el estado superior e inferior, no se esperaría ningún cambio en el campo incidente. Desde

\[p _ {n} - p _ {m} = p _ {n} \left( 1 - \exp \left[ - \beta \hbar \omega _ {m n} \right] \right) \label{11.19}\]

\[\alpha ( \omega ) = \dfrac {4 \pi^{2}} {\hbar c} \omega \left( 1 - e^{- \beta \hbar \omega} \right) \sum _ {n , m} p _ {n} \left| \overline {\mu} _ {m n} \right|^{2} \delta \left( \omega _ {m n} - \omega \right) \label{11.20}\]

Nuevamente el\(\omega _ {m n}\) factor ha sido sustituido por\(\omega\). Ahora podemos separar\(\alpha\) en un producto de factores que representan el campo, y la materia, donde la materia es descrita por\(\sigma ( \omega )\), el lineshape de absorción.

\[\alpha ( \omega ) = \dfrac {4 \pi^{2}} {\hbar c} \omega \left( 1 - e^{- \beta \hbar \omega} \right) \sigma ( \omega ) \label{11.21}\]

\[\sigma ( \omega ) = \sum _ {n , m} p _ {n} \left| \overline {\mu} _ {m n} \right|^{2} \delta \left( \omega _ {m n} - \omega \right) \label{11.22}\]

Para expresar la forma de línea en términos de una función de correlación utilizamos una representación de la función delta a través de una transformada de Fourier de un exponencial complejo:

\[\delta \left( \omega _ {m n} - \omega \right) = \dfrac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d t \,e^{i \left( \omega _ {m n} - \omega \right) t} \label{11.23}\]

escribir

\[\sigma ( \omega ) = \dfrac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d t \sum _ {n , m} p _ {n} \langle n | \overline {\mu} | m \rangle \langle m | \overline {\mu} | n \rangle e^{i \left( \omega _ {m n} - \omega \right) t} \label{11.24}\]

Ahora equiparando

\[U _ {0} | n \rangle = e^{- i H _ {0} t / \hbar} | n \rangle = e^{- i E _ {n} t / \hbar} | n \rangle\]

y reconociendo que nuestra expresión contiene el operador de proyección

\[\sigma ( \omega ) = \dfrac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d t \sum _ {n , m} p _ {n} \langle n | \overline {\mu} | m \rangle \left\langle m \left| U _ {0}^{\dagger} \overline {\mu} U _ {0} \right| n \right\rangle e^{- i \omega t}\]

\[= \dfrac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d t \sum _ {n , m} p _ {n} \left\langle n \left| \overline {\mu} _ {I} ( 0 ) \overline {\mu} _ {I} (t) \right| n \right\rangle e^{- i \omega t} \label{11.25}\]

Pero esta última expresión es solo una función de correlación de momento dipolar: el promedio térmico de equilibrio sobre un par de operadores dipolares dependientes del tiempo:

\[\sigma ( \omega ) = \dfrac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d t e^{- i \omega t} \left\langle \overline {\mu} _ {I} ( 0 ) \overline {\mu} _ {I} (t) \right\rangle \label{11.26}\]

La forma de línea de absorción viene dada por la transformada de Fourier de la función de correlación dipolo. La función de correlación describe el comportamiento dependiente del tiempo o fluctuaciones espontáneas en el momento dipolar en ausencia de campo E y contiene información sobre estados de sistema y ensanchamiento debido a la relajación. Se pueden usar manipulaciones adicionales para cambiar el orden de los operadores tomando el complejo conjugado del exponencial

\[\sigma ( \omega ) = \dfrac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d t e^{i \omega t} \left\langle \overline {\mu} _ {I} (t) \overline {\mu} _ {I} ( 0 ) \right\rangle \label{11.27}\]

y podemos volver a agregar la polarización del campo de luz al elemento de matriz

\[\sigma ( \omega ) = \dfrac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d t e^{i \omega t} \left\langle \hat {\varepsilon} \cdot \overline {\mu} _ {I} (t) \hat {\varepsilon} \cdot \overline {\mu} _ {I} ( 0 ) \right\rangle \label{11.28}\]

para enfatizar el componente orientacional a esta función de correlación. Aquí hemos escrito operadores enfatizando la representación de la imagen de interacción. A medida que avancemos, dejaremos caer esta notación, y la tomaremos como entendido que para fines de espectroscopia, el operador dipolo se expresa en la imagen de interacción y evoluciona bajo el material hamiltoniano\(H_0\).

Lecturas

1. McHale, J. L., Espectroscopia Molecular. 1a ed.; Prentice Hall: Upper Saddle River, NJ, 1999.
2. McQuarrie, D. A., Mecánica Estadística. Harper & Row: Nueva York, 1976; Cap. 21.
3. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006.
4. Schatz, G. C.; Ratner, M. A., Mecánica Cuántica en Química. Publicaciones de Dover: Mineola, NY, 2002; Sección 6.2.