14.1: Fluctuaciones y Aleatoriedad - Algunas Definiciones

“Fluctuaciones” es mi palabra para la evolución temporal de un sistema perturbado al azar en o cerca del equilibrio. Para problemas químicos en la fase condensada nos encontramos constantemente con el problema de fluctuaciones aleatorias a variables dinámicas como resultado de sus interacciones con su entorno. No es razonable pensar que va a llegar a una ecuación de movimiento para la variable determinista interna, pero deberíamos ser capaces de entender el comportamiento estadísticamente y llegar a ecuaciones de movimiento para distribuciones de probabilidad. Los modelos de esta forma se conocen comúnmente como estocásticos. Una ecuación estocástica de movimiento es aquella que incluye un componente aleatorio para el desarrollo del tiempo.

Cuando introdujimos funciones de correlación, discutimos la idea de que una descripción estadística de un sistema se formula comúnmente en términos de funciones de distribución de probabilidad\(P\). Los observables son comúnmente descritos por momentos de esta distribución, los cuales se obtienen integrando sobre\(P\), por ejemplo

\[\left.\begin{aligned} \langle x \rangle & = \int d x \,x \mathrm {P} (x) \\ \left\langle x^{2} \right\rangle & = \int d x \,x^{2} \mathrm {P} (x) \end{aligned} \right. \label{13.1}\]

Para los procesos dependientes del tiempo, reconocemos que es posible que la distribución de probabilidad lleve una dependencia del tiempo.

\[\begin{align} \langle x (t) \rangle & = \int d x \,x (t) \mathrm {P} ( x , t ) \\ \left\langle x^{2} (t) \right\rangle & = \int d x \,x^{2} (t) \mathrm {P} ( x , t ) \label{13.2} \end{align} \]

Las funciones de correlación van un paso más allá y dependen de distribuciones de probabilidad conjuntas\(\mathrm {P} \left( t^{\prime \prime} , A ; t^{\prime} , B \right)\) que dan la probabilidad de observar un valor de\(A\) en el tiempo\(t''\) y un valor de\(B\) en el tiempo\(t'\):

\[\left\langle A \left( t^{\prime \prime} \right) B \left( t^{\prime} \right) \right\rangle = \int d A \int d B \, A B \,\mathrm {P} \left( t^{\prime \prime} , A ; t^{\prime} , B \right)\label{13.3} \]

La descripción estadística de las fluctuaciones aleatorias se describe a través de estas distribuciones de probabilidad dependientes del tiempo, y necesitamos una ecuación estocástica de movimiento para describir su comportamiento. Un ejemplo común de tal proceso es el movimiento browniano, la posición fluctuante de una partícula bajo la influencia de un ambiente térmico.

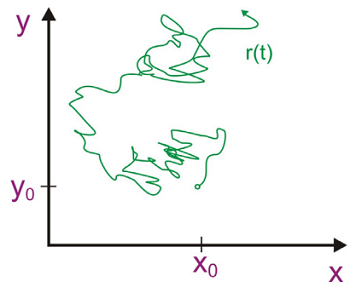
No es práctico describir la posición absoluta de la partícula, pero podemos formular una ecuación de movimiento para la probabilidad de encontrar la partícula en el tiempo y el espacio dado que se conoce su posición inicial. Trabajando a partir de un modelo de caminata aleatoria, se puede derivar una ecuación de movimiento que toma la forma de la conocida ecuación de difusión, aquí escrita en una dimensión:

\[\dfrac {\partial \mathrm {P} ( x , t )} {\partial t} = \mathcal {D} \dfrac {\partial^{2}} {\partial x^{2}} \mathrm {P} ( x , t ) \label{13.4}\]

Aquí\(\mathcal {D}\) está la constante de difusión que establece la escala de tiempo y la extensión espacial del movimiento aleatorio. [Observe la similitud de esta ecuación con la ecuación de Schrödinger dependiente del tiempo para una partícula libre si\(\mathcal {D}\) se toma como imaginaria]. Dada la condición inicial\(\mathrm {P} \left( x , t _ {0} \right) = \delta \left( x - x _ {0} \right)\), la solución es una densidad de probabilidad condicional

\[\mathrm {P} \left( x , t ; x _ {0} , t _ {0} \right) = \dfrac {1} {\sqrt {2 \pi \mathcal {D} \left( t - t _ {0} \right)}} \exp \left( - \dfrac {\left( x - x _ {0} \right)^{2}} {4 \mathcal {D} \left( t - t _ {0} \right)} \right) \label{13.5}\]

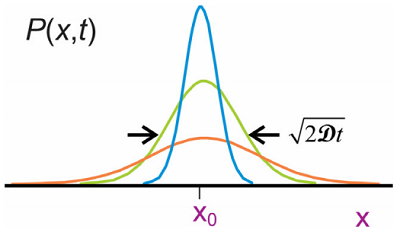
La distribución de probabilidad describe las estadísticas de fluctuaciones en la posición de una partícula promediada a lo largo de muchas trayectorias. Analizando los momentos de esta densidad de probabilidad usando la Ecuación\ ref {13.2} encontramos que

\[\begin{align} \langle x (t) \rangle & = x _ {0} \\[4pt] \left\langle \delta x (t)^{2} \right\rangle & = 2 \mathcal {D} t .\end{align}\]

donde

\[\delta x (t) = x (t) - x _ {0}\]

Entonces, la distribución mantiene una forma gaussiana centrada en\(x_0\), y se amplía con el tiempo como\(2\mathcal {D}t\).

El movimiento browniano es un ejemplo de un proceso gaussiano-markoviano. Aquí Gaussiano se refiere a casos en los que describimos la distribución de probabilidad para una variable\(P(x)\) como una distribución normal gaussiana. Aquí en una dimensión:

\[ \begin{align} \mathrm {P} (x) &= A e^{- \left( x - x _ {0} \right)^{2} / 2 \Delta^{2}} \\[4pt] \Delta^{2} &= \left\langle x^{2} \right\rangle - \langle x \rangle^{2} \label{13.6} \end{align}\]

La distribución gaussiana es importante, porque el teorema del límite central establece que la distribución de una variable aleatoria continua con varianza finita seguirá a la distribución gaussiana. Las distribuciones gaussianas también están completamente definidas en términos de su primer y segundo momento, lo que significa que una densidad de probabilidad dependiente del tiempo\(P(x,t)\) se caracteriza únicamente por un valor medio en la variable observable\(x\) y una función de correlación que describe las fluctuaciones en\(x\). Las distribuciones gaussianas para sistemas en equilibrio térmico también son importantes para la relación entre las distribuciones gaussianas y las superficies de energía libre parabólica:

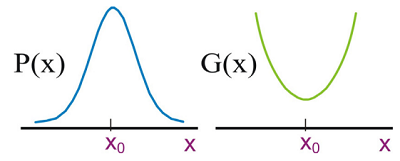
\[G (x) = - k _ {B} T \ln \mathrm {P} (x) \label{13.7}\]

Si la densidad de probabilidad es gaussiana a lo largo\(x\), entonces la energía libre del sistema proyectada sobre esta coordenada (a menudo denominada potencial de fuerza media) tiene una forma armónica. Por lo tanto, las estadísticas gaussianas son efectivas para describir las fluctuaciones sobre un valor medio de equilibrio\( x_o\).

Markoviano significa que el comportamiento dependiente del tiempo de un sistema no depende de su historia anterior, estadísticamente hablando. Naturalmente el estado de cualquier molécula depende de su trayectoria a través del espacio de fases, sin embargo estamos diciendo que desde la perspectiva de un conjunto no hay memoria del estado del sistema en un momento anterior. Esto se puede afirmar en términos de funciones de probabilidad conjunta como

\[\mathrm {P} \left( x _ {2} , t _ {2} ; x _ {1} , t _ {1} ; x _ {0} , t _ {0} \right) = \mathrm {P} \left( x _ {2} , t _ {2} ; x _ {1} , t _ {1} \right) \mathrm {P} \left( x _ {1} , t _ {1} ; x _ {0} , t _ {0} \right)\]

o

\[\mathrm {P} \left( t _ {2} ; t _ {1} ; t _ {0} \right) = \mathrm {P} \left( t _ {2} ; t _ {1} \right) \mathrm {P} \left( t _ {1} ; t _ {0} \right)\]

La probabilidad de observar una trayectoria que te lleve del estado 1 en el tiempo 1 al estado 2 en el tiempo 2 no depende de donde estuvieras en el tiempo 0. Además, dado el conocimiento de la probabilidad de ejecutar cambios durante un solo intervalo de tiempo, se puede describir exactamente\(P\) para cualquier intervalo de tiempo. Por lo tanto, Markovic se refiere a procesos dependientes del tiempo en una escala de tiempo larga en comparación con el tiempo de correlación para la variable interna que le importa. Por ejemplo, la ecuación de difusión solo se mantiene después de que la partícula haya experimentado suficientes colisiones con su entorno que no tenga memoria de su posición e impulso anteriores:\(t > \tau_c\).

Lecturas

1. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Ch. 1.5 y Ch. 7.