15.2: Transferencia de Energía por Resonancia de Förster (FRET)

La transferencia de energía por resonancia de Förster (FRET) se refiere a la transferencia no radiativa de una excitación electrónica de una molécula donante a una molécula aceptora:

\[\ce{D}^{*} + \ce{A} \rightarrow \ce{D} + \ce{A}^{*} \label{14.1}\]

Esta transferencia electrónica de excitación, cuya descripción práctica fue dada por primera vez por Förster, surge de una interacción dipolo-dipolo entre los estados electrónicos del donante y el aceptor, y no implica la emisión y reabsorción de un campo de luz. La transferencia ocurre cuando las oscilaciones de una coherencia electrónica inducida ópticamente en el donante son resonantes con la brecha de energía electrónica del aceptor. La fuerza de la interacción depende de la magnitud de una interacción dipolo de transición, que depende de la magnitud de los elementos de la matriz de transición donador y aceptor, y de la alineación y separación de los dipolos. La fuerte\(1/r^6\) dependencia de la distancia se utiliza a menudo en la caracterización espectroscópica de la proximidad de donante y aceptor.

Los estados electrónicos terrestres y excitados de las moléculas donadoras y aceptoras juegan un papel en FRET. Consideramos el caso en el que hemos excitado la transición electrónica del donante, y el aceptador se encuentra en el estado fundamental. La absorción de luz por parte del donante en la brecha de energía de equilibrio es seguida por una rápida relajación vibratoria que disipa la energía de reorganización del donante en el\(\lambda _ {D}\) transcurso de picosegundos. Esto deja al donante en una coherencia que oscila en la brecha energética en el estado excitado del donante\(\omega _ {e g}^{D} \left( q _ {D} = d _ {D} \right)\). La escala de tiempo para FRET suele ser nanosegundos, por lo que esta etapa de preparación suele ser mucho más rápida que la fase de transferencia. Para la transferencia de energía de resonancia se requiere una condición de resonancia, de modo que la oscilación de la coherencia del donante excitado sea resonante con la brecha de energía electrónica del estado fundamental del aceptor\(\omega _ {e g}^{A} \left( q _ {A} = 0 \right)\). La transferencia de energía al aceptor conduce a la relajación vibracional y la posterior fluorescencia del aceptor que se desplaza espectralmente de la fluorescencia del donante. En la práctica, la eficiencia de la transferencia de energía se obtiene comparando la fluorescencia emitida por el donante y el aceptor.

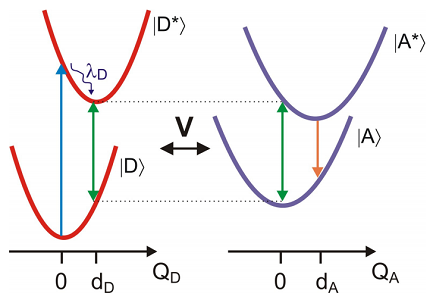
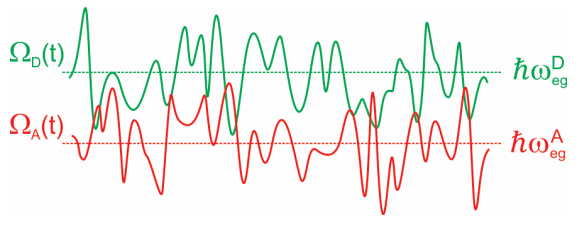
Esta descripción del problema se presta naturalmente a tratar con un DHO hamiltoniano, sin embargo, también es aplicable un cuadro alterno, que puede describirse a través del EG Hamiltoniano. FRET surge de la resonancia que ocurre cuando la brecha de energía electrónica fluctuante de un donante en su estado excitado coincide con la brecha de energía de un aceptor en su estado fundamental. En otras palabras

\[\underbrace {\hbar \omega _ {e g}^{D} - \lambda _ {D}} _ {\Omega _ {D} (t)} = \underbrace {\hbar \omega _ {e g}^{A} - \lambda _ {A}} _ {\Omega _ {A} (t)} \label{14.2}\]

Estas brechas de energía dependen del tiempo con cruces de ocasión que permiten la transferencia de energía.

Nuestro sistema incluye los potenciales terrestres y excitados de las moléculas donadoras y aceptoras. Las cuatro posibles configuraciones electrónicas del sistema son

\[| G _ {D} G _ {A} \rangle , | E _ {D} G _ {A} \rangle , | G _ {D} E _ {A} \rangle , | E _ {D} E _ {A} \rangle\]

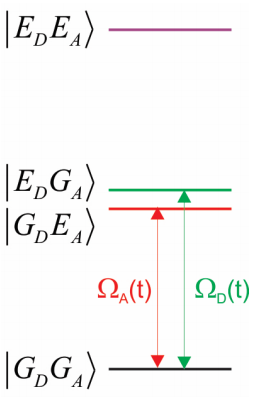
Aquí la notación se refiere a los estados vibrónicos ground (\(G\)\(E\)) o excitado () de donador (\(D\)) o aceptor (\(A\)). Más explícitamente, los estados también incluyen la excitación vibracional:

\[| E _ {D} G _ {A} \rangle = | e _ {D} n _ {D} ; g _ {A} n _ {A} \rangle\]

Así, el sistema no puede tener excitación, una excitación en el donante, una excitación en el aceptor, o una excitación tanto en el donante como en el aceptor. Para nuestros propósitos, consideremos solo las dos configuraciones electrónicas que son cercanas en energía, y que probablemente jugarán un papel en la transferencia de resonancia en la Ecuación\ ref {14.2} y

\(| E _ {D} G _ {A} \rangle\)y\(| G _ {D} E _ {A} \rangle\)

Dado que el donante y el aceptor están débilmente acoplados, podemos escribir nuestro hamiltoniano para este problema en una forma que puede resolverse mediante la teoría de la perturbación (\(H = H _ {0} + V\)). Trabajando con el enfoque DHO. nuestro material Hamiltoniano cuenta con cuatro colectores electrónicos a considerar:

\[\underbrace {\hbar \omega _ {e g}^{D} - \lambda _ {D}} _ {\Omega _ {D} (t)} = \underbrace {\hbar \omega _ {e g}^{A} - \lambda _ {A}} _ {\Omega _ {A} (t)} \label{14.3}\]

Cada uno de estos se define como lo hacíamos anteriormente, con una energía electrónica y una dependencia de una coordenada nuclear desplazada. Por ejemplo

\[\begin{align} H _ {D}^{E} &= | e _ {D} \rangle E _ {e}^{D} \langle e _ {D} | + H _ {e}^{D} \label{14.4} \\[4pt] H _ {e}^{D} &= \hbar \omega _ {0}^{D} \left( \tilde {p} _ {D}^{2} + \left( \tilde {q} _ {D} - \tilde {d} _ {D} \right)^{2} \right) \label{14.5} \end{align}\]

\(E _ {e}^{D}\)es la energía electrónica del estado excitado del donante.

Entonces, ¿qué es\(V\)? Clásicamente es una interacción Coulomb de la forma,

\[V = \sum _ {i j} \frac {q _ {i}^{D} q _ {j}^{A}} {\left| r _ {i}^{D} - r _ {j}^{A} \right|} \label{14.6}\]

Aquí la suma está sobre todos los electrones y núcleos del donante (\(i\)) y aceptor (\(j\)).

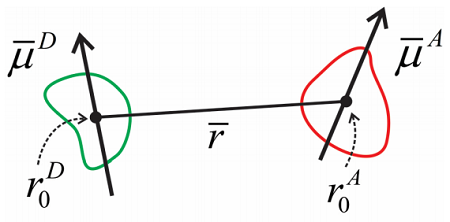
Como es, es difícil trabajar con esto, pero en general la separación entre moléculas, podemos reformular esto como una interacción dipolo-dipolo. Definimos un marco de referencia para la molécula donante y aceptora, y asumimos que la distancia entre moléculas es grande. Entonces los momentos dipolares para las moléculas son

\[\begin{aligned} \overline {\mu}^{D} & = \sum _ {i} q _ {i}^{D} \left( r _ {i}^{D} - r _ {0}^{D} \right) \\ \overline {\mu}^{A} & = \sum _ {j} q _ {j}^{A} \left( r _ {J}^{A} - r _ {0}^{A} \right) \end{aligned} \label{14.7}\]

La interacción entre donante y aceptor toma la forma de una interacción dipolo-dipolo:

\[V = \dfrac {3 \left( \overline {\mu} _ {A} \cdot \hat {r} \right) \left( \overline {\mu} _ {D} \cdot \hat {r} \right) - \overline {\mu} _ {A} \cdot \overline {\mu} _ {D}} {\overline {r}^{3}} \label{14.8}\]

donde\(r\) es la distancia entre los dipolos donador y aceptor y\(\hat{r}\) es un vector unitario que marca la dirección entre ellos. Los operadores de dipolo aquí se toman para actuar únicamente sobre los estados electrónicos y ser independientes de la configuración nuclear, es decir, la aproximación del Condón. Escribimos los elementos de la matriz dipolo de transición que acoplan los estados electrónicos terrestres y excitados para el donante y el aceptor como

\[ \begin{align} \overline {\mu} _ {A} &= | A \rangle \overline {\mu}_{AA^{*}} \left\langle A^{*} | + | A^{*} \right\rangle \overline {\mu} _ {A^{*} A} \langle A | \label{14.9} \\[4pt] \overline {\mu} _ {D} &= | D \rangle \overline {\mu} _ {D D^{*}} \left\langle D^{*} | + | D^{*} \right\rangle \overline {\mu} _ {D^{*} D} \langle D | \label{14.10} \end{align} \]

Para el operador dipolo, podemos separar las contribuciones escalares y orientacionales como

\[\overline {\mu} _ {A} = \hat {u} _ {A} \mu _ {A} \label{14.11}\]

Esto permite que la interacción dipolo de transición en la Ecuación\ ref {14.8} se escriba como

\[V = \mu _ {A} \mu _ {B} \frac {\kappa} {r^{3}} [ | D^{*} A \rangle \left\langle A^{*} D | + | A^{*} D \right\rangle \left\langle D^{*} A | \right] \label{14.12}\]

Todos los factores orientacionales están ahora en el término\(\kappa\)

\[\kappa = 3 \left( \hat {u} _ {A} \cdot \hat {r} \right) \left( \hat {u} _ {D} \cdot \hat {r} \right) - \hat {u} _ {A} \cdot \hat {u} _ {D} \label{14.13}\]

Ahora podemos obtener las tasas de transferencia de energía utilizando la Regla de Oro de Fermi expresada como una función de correlación en la interacción Hamiltoniana:

\[w _ {k \ell} = \frac {2 \pi} {\hbar^{2}} \sum _ {\ell} p _ {\ell} \left| V _ {k \ell} \right|^{2} \delta \left( \omega _ {k} - \omega _ {\ell} \right) = \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \left\langle V _ {I} (t) V _ {I} ( 0 ) \right\rangle \label{14.14}\]

¡Tenga en cuenta que esto no es una transformada de Fourier! Dado que estamos usando una función de correlación se supone que tenemos un sistema de equilibrio, aunque inicialmente estemos en el estado donante excitado. Esto es razonable para el caso de que exista una clara separación de escala de tiempo entre la relajación vibracional ps y la termalización en el estado excitado del donante y la escala de tiempo (o tasa inversa) del proceso de transferencia de energía.

Ahora sustituyendo el estado inicial\(\ell = | D^{*} A \rangle\) y el estado final\(k = | A^{*} D \rangle\), encontramos

\[w _ {E T} = \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \frac {\left\langle \kappa^{2} \right\rangle} {r^{6}} \left\langle D^{*} A \left| \mu _ {D} (t) \mu _ {A} (t) \mu _ {D} ( 0 ) \mu _ {A} ( 0 ) \right| D^{*} A \right\rangle \label{14.15}\]

donde

\[\mu _ {D} (t) = e^{i H _ {D} t / \hbar} \mu _ {D} e^{- i H _ {D} t / \hbar}.\]

Aquí, hemos descuidado el movimiento rotacional de los dipolos. En general, el promedio orientacional es

\[\left\langle \kappa^{2} \right\rangle = \langle \kappa (t) \kappa ( 0 ) \rangle \label{14.16}\]

Sin embargo, este factor es más fácil de evaluar si los dipolos son estáticos, o si giran rápidamente para distribuirse isotrópicamente. Para el caso estático\(\left\langle \kappa^{2} \right\rangle = 0.475\). Para el caso de pérdida rápida de orientación:

\[\left\langle \kappa^{2} \right\rangle \rightarrow \langle \kappa (t) \rangle \langle \kappa ( 0 ) \rangle = \langle \kappa \rangle^{2} = \dfrac{2}{3}\]

Dado que los operadores de dipolo actúan solo sobre\(A\) o\(D^{*}\),\(D\) y las coordenadas y\(A\) nucleares son ortogonales, podemos separar términos en los estados donante y aceptor.

\[\begin{aligned} w _ {E T} & = \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \frac {\left\langle \kappa^{2} \right\rangle} {r^{6}} \left\langle D^{*} \left| \mu _ {D} (t) \mu _ {D} ( 0 ) \right| D^{*} \right\rangle \left\langle A \left| \mu _ {A} (t) \mu _ {A} ( 0 ) \right| A \right\rangle \\ & = \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \frac {\left\langle \kappa^{2} \right\rangle} {r^{6}} C _ {D^{*} D^{*}} (t) C _ {\mathrm {AA}} (t) \end{aligned} \label{14.17}\]

Los términos de esta ecuación representan la función de correlación dipolo para el donante que inicia en el estado excitado y la función de correlación aceptora que inicia en el estado fundamental. Es decir, estas son funciones de correlación para la emisión del donante (fluorescencia) y la absorción del aceptor. Recordando que\(| D^{*} \rangle\) representa la configuración electrónica y nuclear\(| d^{*} n _ {D^{*}} \rangle\), podemos utilizar el oscilador armónico desplazado Hamiltoniano o la brecha de energía Hamiltoniano para evaluar las funciones de correlación. Para el caso de la estadística gaussiana podemos escribir

\[C _ {D _ {D}^{*}} \cdot (t) = \left| \mu _ {D D^{*}} \right|^{2} e^{- i \left( \omega _ {D D^{*}} - 2 \lambda _ {D} \right) t^{*} - g _ {D}^{*} (t)} \label{14.18}\]

\[C _ {A A} (t) = \left| \mu _ {A A} \right|^{2} e^{- i \omega _ {A A} t - g _ {A} (t)} \label{14.19}\]

Aquí hicimos uso de

\[ \omega _ {D^{*} D} = \omega _ {D D^{*}} - 2 \lambda _ {D}\label{14.20}\]

que expresa la frecuencia de emisión como un desplazamiento de frecuencia\(2 \lambda _ {D}\) relativa a la frecuencia de absorción del donante. Las funciones de correlación dipolo se pueden expresar en términos de las transformadas inversas de Fourier de una forma de línea de fluorescencia o absorción:

\[C _ {D^{*} D^{\cdot}} (t) = \frac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d \omega e^{- i \omega t} \sigma _ {f l u o r}^{D} ( \omega ) \label{14.21}\]

\[C _ {A A} (t) = \frac {1} {2 \pi} \int _ {- \infty}^{+ \infty} d \omega e^{- i \omega t} \sigma _ {a b s}^{A} ( \omega ) \label{14.22}\]

Para expresar la tasa de transferencia de energía en términos de su forma práctica común, hacemos uso del Teorema de Parsival, que establece que si se define un par de transformada de Fourier para dos funciones, la integral sobre un producto de esas funciones es igual ya sea evaluada en el dominio del tiempo o de la frecuencia:

\[\int _ {- \infty}^{\infty} f _ {1} (t) f _ {2}^{*} (t) d t = \int _ {- \infty}^{\infty} \tilde {f} _ {1} ( \omega ) \tilde {f} _ {2}^{*} ( \omega ) d \omega \label{14.23}\]

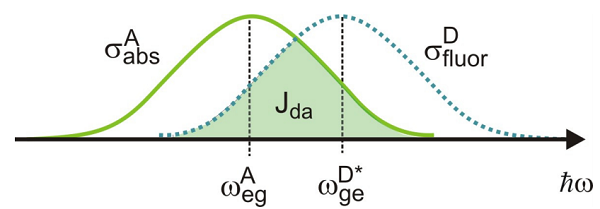
Esto nos permite expresar la velocidad de transferencia de energía como una integral de solapamiento\(J_{DA}\) entre los espectros de fluorescencia donante y aceptor abso rption:

\[w _ {E T} = \frac {1} {\hbar^{2}} \frac {\left\langle \kappa^{2} \right\rangle} {r^{6}} \left| \mu _ {D D^{*}} \right|^{2} \left| \mu _ {A A^{\prime}} \right|^{2} \int _ {- \infty}^{+ \infty} d \omega \sigma _ {a b s}^{A} ( \omega ) \sigma _ {f u o r}^{D} ( \omega ) \label{14.24}\]

Aquí está la forma de línea normalizada al elemento de la matriz de transición al cuadrado:\(\sigma = \sigma / | \mu |^{2}\). La integral de superposición es una medida de resonancia entre las transiciones donador y aceptor.

Entonces, la tasa de transferencia de energía se escala como\(r^{-6}\), depende de las fuerzas de las transiciones electrónicas para las moléculas donadoras y aceptoras, y requiere resonancia entre la fluorescencia del donante y la absorción del aceptor. Una de las cosas que hemos descuidado es que la tasa de transferencia de energía también dependerá de la tasa de relajación emocionada de la población del estado donante. Dado que esta relajación está típicamente dominada por la tasa de fluorescencia del donante, la tasa de transferencia de energía se escribe comúnmente en términos de una distancia\(R_0\) efectiva y la vida útil de la fluorescencia del donante\(\tau_D\):

\[w _ {E T} = \frac {1} {\tau _ {D}} \left( \frac {R _ {0}} {r} \right)^{6} \label{14.25}\]

A la distancia de transferencia crítica\(R_0\) la tasa (o probabilidad) de transferencia de energía es igual a la tasa de fluorescencia. \(R_0\)se define en términos de la sexta raíz de los términos en la Ecuación\ ref {14.24}, y se escribe comúnmente como

\[R _ {0}^{6} = \frac {9000 \ln ( 10 ) \phi _ {D} \left\langle \kappa^{2} \right\rangle} {128 \pi^{5} n^{4} N _ {A}} \int _ {0}^{\infty} d \overline {\nu} \frac {\sigma _ {\text {fluur}}^{D} ( \overline {V} ) \varepsilon _ {A} ( \overline {v} )} {\overline {V}^{4}} \label{14.26}\]

Esta es la definición práctica que da cuenta de la dependencia de frecuencia de la interacción del dipolo de transición y la relajación no radiativa del donante además de expresarse en unidades comunes. \(\overline {V}\)representa unidades de frecuencia en cm ^-1. El espectro de fluorescencia\(\sigma_{\text {fluor}}^{D}\) debe normalizarse a la unidad de área, de manera que at\(\sigma_{\text {fluor }}^{D}(\bar{v})\) se exprese en cm (números de onda inversos). El espectro de absorción\(\varepsilon_{A}(\bar{v})\) debe expresarse en unidades de coeficiente de extinción decádica molar (litro/mol*cm). \(n\)es el índice de refracción del disolvente,\(N_A\) es el número de Avagadro y\(\phi_D\) es el rendimiento cuántico de fluorescencia del donante.

Interacción del dipolo de transición

FRET es un ejemplo de una interacción de dipolo de transición mecánica cuántica. La interacción entre dos dipolos,\(A\) y\(D\), en la Ecuación\ ref {14.12} es

\[V = \frac {\kappa} {r^{3}} \left\langle e \left| \mu _ {A} \right| g \right\rangle \left\langle g \left| \mu _ {D} \right| e \right\rangle \label{14.27}\]

Aquí,\(\left\langle g \left| \mu _ {D} \right| e \right\rangle\) está el momento dipolar de transición en Debye para la transición de estado tierra a excitado de la molécula\(A\). \(r\)es la distancia entre los centros de los dipolos puntuales, y\(\kappa\) es el factor orientacional sin unidades

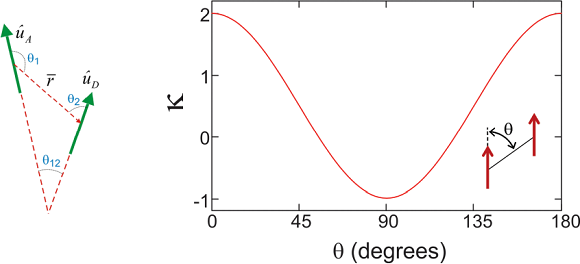
\[\kappa = 3 \cos \theta _ {1} \cos \theta _ {2} - \cos \theta _ {12}\]

La siguiente figura ilustra esta función para el caso de dos dipolos paralelos, en función del ángulo entre el dipolo y el vector que define su separación.

En el caso del acoplamiento vibracional, el operador dipolo se expande en la coordenada normal vibracional:\(\mu = \mu _ {0} + \left( \partial \mu / \partial Q _ {A} \right) Q _ {A}\) y los elementos de la matriz de dipolo de transición armónica son

\[\left\langle 1\left|\mu_{A}\right| 0\right\rangle=\sqrt{\frac{\hbar}{2 c \omega_{A}}} \frac{\partial \mu}{\partial Q_{A}} \label{14.28}\]

donde\(\omega _ {A}\) está la frecuencia vibracional. Si la frecuencia\(V _ {A}\) se da en cm ^-1, y el momento dipolar de transición\(\partial \mu / \partial Q _ {A}\) se da en unidades de\(\begin{equation}\text { D } Å^{-1} \text {amu }^{-1 / 2}\end{equation}\), entonces el elemento matriz en unidades de\(D\) es

\[\left| \left\langle 1 \left| \mu _ {A} \right| 0 \right\rangle \right| = 4.1058 v _ {A}^{- 1 / 2} \left( \partial \mu / \partial Q _ {A} \right)\]

Si la distancia entre dipolos se especifica en Ångstroms, entonces el acoplamiento de dipolo de transición de la Ecuación\ ref {14.27} en cm ^-1 es

\[V \left( c m^{- 1} \right) = 5034 \kappa r^{- 3}.\]

Experimentalmente, se puede determinar el momento dipolar de transición a partir de la absorbancia\(A\) como

\[A = \left( \frac {\pi N _ {A}} {3 c^{2}} \right) \left( \frac {\partial \mu} {\partial Q _ {A}} \right)^{2} \label{14.29}\]

Lecturas

1. Cheam, T. C.; Krimm, S., Interacción dipolo de transición en polipéptidos: Ab initio cálculo de parámetros de dipolo de transición. Letras de Física Química 1984, 107, 613-616.
2. Forster, T., Mecanismos de transferencia de excitación electrónica. Discusiones de la Sociedad Faraday 1959, 27, 7-17.
3. Förster, T., Zwischenmolekulare Energiewanderung und Fluoreszenz. Annenen der Physik 1948, 437, 55-75.
4. Förster, T., Experimentelle und theoretische Untersuchung des zwischenmolecularen Uebergangs von Electronenanregungsenergie. Z. Naturforsch 1949, 4A, 321—327