15.3: Excitones en Agregados Moleculares

Los espectros de absorción de matrices periódicas de cromóforos moleculares que interactúan muestran características espectrales únicas que dependen del tamaño del sistema y del desorden del ambiente. Investigaremos algunas de estas características, centrándonos en los autoestados deslocalizados de estos cromóforos acoplados, conocidos como excitones. Estos principios se aplican al estudio de cristales moleculares, agregados J, fotosensibilizadores y complejos fotocosechadores en la fotosíntesis. Temas similares se utilizan en la descripción de propiedades de polímeros conjugados y fotovoltaica orgánica, y para estados vibracionales extendidos en espectroscopía IR y Raman.

Transferencia de energía en el límite de acoplamiento fuerte

Un fuerte acoplamiento entre moléculas conduce a la deslocalización de estados propios electrónicos o vibracionales, bajo los cuales no se aplican modelos de acoplamiento débil como FRET. De nuestros estudios del sistema acoplado de dos estados, sabemos que cuando el acoplamiento entre estados es mucho mayor que la división de energía entre los estados (\(\varepsilon _ {1} - \varepsilon _ {2} \ll 2 \mathrm {V}\)) entonces los autoestados resultantes\(| \pm \rangle\) son combinaciones simétricas y antisimétricas igualmente ponderadas de los dos, cuyos valores propios de energía están divididos por\(2V\). Ajuste\(\varepsilon _ {1} = \varepsilon _ {2} = \varepsilon\)

\[E _ {\pm} = \varepsilon \pm V\]

\[| \pm \rangle = \frac {1} {\sqrt {2}} ( | 1 \rangle \pm | 2 \rangle )\]

Si excitamos una de estas moléculas, esperamos que la excitación fluya de un lado a otro a la frecuencia de Rabi. Entonces, ¿qué sucede con los cromóforos acoplados múltiples, centrando particular interés en la colocación de cromóforos acoplados en matrices periódicas en el espacio? En el régimen de acoplamiento fuerte, la variación en las energías desacopladas es pequeña, lo que lo convierte en un problema de estados cuasi-degenerados acoplados. Con una estructura espacialmente de período, los estados resultantes tienen una similitud cercana a las descripciones simples de la estructura de banda electrónica usando el modelo de unión estrecha.

Excitones

Los excitones se refieren a estados excitados electrónicos que no se localizan en una molécula en particular. Pero más allá de eso hay muchos sabores. Nos concentraremos en los excitones de Frenkel, que hacen referencia a estados excitados en los que el electrón excitado y el correspondiente agujero (o vacante de electrones) residen en la misma molécula. Todas las moléculas permanecen eléctricamente neutras en el suelo y estados excitados. Esto corresponde a lo que uno esperaría cuando uno tiene interacciones resonantes dipolo-dipolo entre moléculas. Cuando hay carácter de transferencia de carga, el electrón y el agujero pueden residir en diferentes moléculas del complejo acoplado. A estos se les conoce como excitones Mott—Wannier.

Espectro de Absorción del Dímero Molecular

Para describir la espectroscopia de una matriz de muchos cromóforos acoplados, primero es instructivo trabajar a través de un par de moléculas acopladas. Este es en esencia el problema de dos niveles de antes. Consideramos un par de moléculas (\(1\)y\(2\)), cada una de las cuales tiene un estado molido y electrónicamente excitado\(| e \rangle\) y\(| g \rangle\)) dividido por una brecha de energía\(\varepsilon 0\), y un momento dipolar de transición\(\overline {\mu}\). En ausencia de acoplamiento, el estado del sistema puede especificarse especificando el estado electrónico de ambas moléculas, conduciendo a cuatro estados posibles:\(|g g\rangle,|e g\rangle,|g e\rangle,|e e\rangle\) cuyas energías son\(0, \varepsilon_{0,} \varepsilon_{0}\), y\(2 \varepsilon 0\), respectivamente.

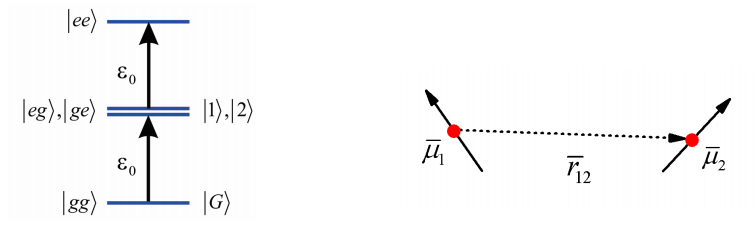
Para taquigrafía definimos el estado fundamental como\(|G\rangle\) y los estados excitados como\(|1\rangle\) y\(|2\rangle\) para significar la excitación electrónica está en cualquiera de las moléculas\(1\) o\(2\). Además, las moléculas están espaciadas por una separación\(r_{12}\), y hay una interacción dipolo de transición que acopla las moléculas.

\[V = J ( | 2 \rangle \langle 1 | + | 1 \rangle \langle 2 | )\]

Siguiendo nuestra descripción del acoplamiento de dipolo de transición, la fuerza del acoplamiento\(J\) viene dada por

\[J=\frac{\left(\bar{\mu}_{1} \cdot \bar{\mu}_{2}\right)\left|\bar{r}_{12}\right|^{2}-3\left(\bar{\mu}_{1} \cdot \bar{r}_{12}\right)\left(\bar{\mu}_{2} \cdot \bar{r}_{12}\right)}{\left|\bar{r}_{12}\right|^{5}}=\frac{\mu_{1} \mu_{2}}{r_{12}^{3}} \kappa\]

donde el factor orientacional es

\[\kappa=\left(\hat{\mu}_{1} \cdot \hat{\mu}_{2}\right)-3\left(\hat{\mu}_{1} \cdot \hat{r}_{12}\right)\left(\hat{\mu}_{2} \cdot \hat{r}_{12}\right)\]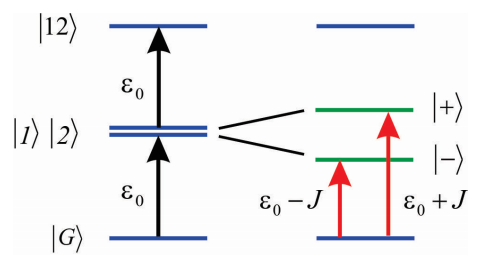

Asumimos que el acoplamiento no es demasiado fuerte, de manera que solo podemos concentrarnos en cómo influye\(|1 \rangle\) y\(|2 \rangle\) pero no\(|G \rangle\). Entonces solo necesitamos describir los desplazamientos inducidos por acoplamiento a los estados individualmente excitados, los cuales son descritos por los hamiltonianos

\[H = \left( \begin{array} {l l} {\varepsilon _ {0}} & {J} \\ {J} & {\varepsilon _ {0}} \end{array} \right)\]

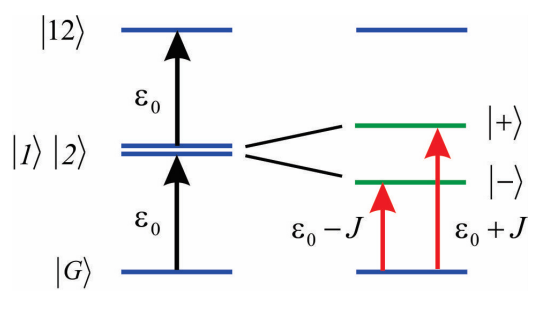
Como se indicó anteriormente, encontramos que los valores propios son

\[E _ {\pm} = \varepsilon _ {0} \pm J\]

y que los autoestados son:

\[|\pm\rangle=\frac{1}{\sqrt{2}}(|1\rangle \pm|2\rangle)\]

Estos estados simétricos y antisimétricos se deslocalizan a través de las dos moléculas, y en el lenguaje de Frenkel los excitones se denominan estados de un excitón. Además, el operador dipolo para el dímero es

\[\overline {M} = \overline {\mu} _ {1} + \overline {\mu} _ {2}\]

y así los elementos de la matriz dipolo de transición son:

\[M _ {\pm} = \langle \pm | \overline {M} | G \rangle = \frac {1} {\sqrt {2}} \left( \overline {\mu} _ {1} \pm \overline {\mu} _ {2} \right)\]

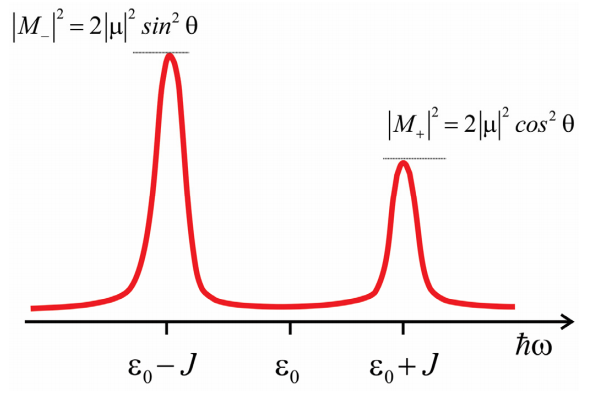
\(M_+\)y\(M_-\) están orientados perpendiculares entre sí en el marco molecular. Si limitamos los dipolos moleculares a estar dentro de un plano, con un ángulo\(2 \theta\) entre ellos, entonces la amplitud de M+ y M- viene dada por

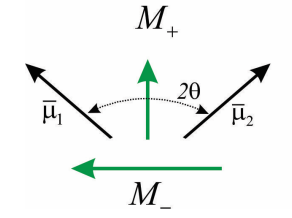
\ begin {array} {l}
M_ {+} =2\ mu\ cos\ theta\\
M_ {-} =2\ mu\ sin\ theta
\ end {array}

Ahora podemos predecir el espectro de absorción para el dímero. Tenemos dos transiciones desde el estado fundamental y los\(| \pm \rangle\) estados que son resonantes en\(\hbar \omega = \varepsilon _ {0} \pm J\) y que tienen una amplitud\(\left| M _ {*} \right|^{2}\). La división entre los picos se conoce como la división Davydov. Obsérvese que la amplitud relativa de los picos permite inferir el ángulo entre los dipolos de transición molecular. También, nota para\(θ = 0°\) o\(90°\), toda la amplitud aparece en una transición con magnitud\(2 | \mu |^{2}\), que se conoce como superradiante.

Excitones de Frenkel con condiciones de límite periódicas

Ahora consideremos agregado lineal de moléculas dispuestas\(N\) periódicamente. Supondremos que cada molécula es un sistema electrónico de dos niveles con un estado fundamental y un estado excitado. Supondremos que la excitación electrónica mueve un electrón desde el estado fundamental a un orbital desocupado de la misma molécula. Marcaremos las moléculas con valores enteros (\(n\)) entre\(0\) y\(N-1\):

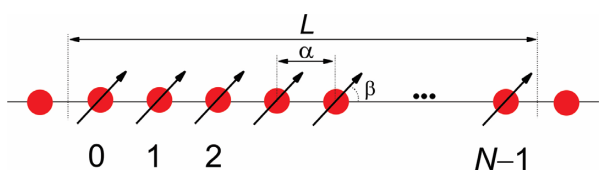
Si las moléculas están separadas a lo largo de la cadena por un espaciado reticular\(a\), entonces el tamaño de la cadena es\(L = \alpha N\). Cada molécula tiene un momento dipolar de transición\(\mu\), que forma un ángulo\(\beta\) con el eje de la cadena.

En ausencia de interacciones, podemos especificar el estado del sistema exactamente identificando si cada molécula está en el estado electrónicamente excitado o fundamental. Si el estado de la molécula n dentro de la cadena es\(\varphi _ {n}\), que puede tomar valores de\(g\) o\(e\), entonces

\[| \psi \rangle = | \varphi _ {0} , \varphi _ {1} , \varphi _ {2} \cdots \varphi _ {n} \cdots \varphi _ {N - 1} \rangle\]

Esta representación del estado del sistema es referida como la base del sitio, ya que se expresa en términos de cada sitio molecular en la cadena. Por simplicidad escribimos el estado fundamental del sistema como

\[| G \rangle = | g , g , g \ldots , g \rangle\]

Si excitamos una de las moléculas dentro del agregado, tenemos un estado de excitación individual en el que se excita la enésima molécula, de modo que

\[| \psi \rangle = | g , g , g , \ldots , e , \dots , g \rangle \equiv | n \rangle\]

Para taquigrafía, identificamos este estado del producto como el\(| n \rangle\) cual debe distinguirse de la función propia molecular en el sitio\(n\),\(\varphi _ {n}\).

Al estado excitado individualmente se le asigna una energía\(\mathcal {E} _ {0}\) correspondiente a la brecha de energía electrónica. En ausencia de acoplamiento, los estados excitados individualmente son\(N\) -veces degenerados, lo que corresponde a una sola excitación en cualquiera de los\(N\) sitios. Si se colocan dos excitaciones en la cadena podemos ver que hay estados\(N(N-1)\) posibles con energía\(2 \varepsilon _ {0}\), reconociendo que el principio Pauli no permite dos excitaciones en un mismo sitio. Cuando se introduce el acoplamiento, la mezcla de estos estados degenerados conduce a las bandas de un excitón y dos excitones. Para esta discusión, nos concentraremos en los estados de un excitón.

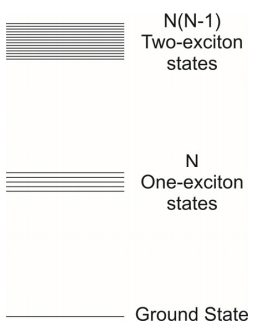
El acoplamiento entre molécula\(n\) y molécula\(n′\) viene dado por el elemento matriz\(V _ {n n^{\prime}}\). Supondremos que una molécula interactúa solo con sus vecinos, y que cada interacción por pares tiene una magnitud\(J\)

\[V _ {n n^{\prime}} = J \delta _ {n , n^{\prime} \pm 1}\]

Si\(V\) es una interacción dipolo-dipolo, el factor orientacional\(\kappa\) dicta que cuando el ángulo del dipolo de transición\(\beta < 54.7^{\circ}\) entonces el signo del acoplamiento\(J < 0\), que es el caso conocido como agregados J (después de Edwin Jelley), e implica una pila de desplazamiento de cromóforos o cabeza- arreglo a cola. Si\(\beta > 54.7^{\circ}\) entonces\(J > 0\), y el sistema se conoce como agregado H.

Para comenzar, también aplicamos condiciones de límite periódicas a este problema, lo que implica que estamos describiendo los estados de una cadena N-molécula dentro de una cadena lineal infinita. En cuanto al hamiltoniano, las moléculas al principio y al final de nuestra cadena sienten las mismas interacciones simétricas con dos vecinos que las otras moléculas. Para escribir esto en términos de una\(N \times N\) matriz finita, uno empareja al primer y último miembro de la cadena:\(J _ {0 , N - 1} = J _ {N - 1,0} = J\)

\[J _ {0 , N - 1} = J _ {N - 1,0} = J.\]

Con estas observaciones en mente, podemos escribir el Frenkel Exciton Hamiltonian para el agregado lineal en términos de un sistema hamiltoniano que refleja los sitios individuales y sus acoplamientos

\[\begin{align} H _ {0} &= H _ {S} + V \\[4pt] H _ {S} &= \sum _ {n = 1}^{N} \varepsilon _ {0} | n \rangle \langle n | \\[4pt] V &= \sum _ {n = 1}^{N} J \{| n^{\prime} \rangle \langle n | + | n \rangle \left\langle n^{\prime} | \right\} \delta _ {n , n^{\prime} \pm 1} \label{14.30} \end{align}\]

Aquí las condiciones de límite periódicas implican que reemplazamos\(| N \rangle \Rightarrow | 0 \rangle\) y\(| - 1 \rangle \Rightarrow | N - 1 \rangle\) dónde aparecen.

Las propiedades ópticas del agregado se obtendrán determinando los estados propios del Hamiltoniano. Buscamos soluciones que describan los estados propios de un excitón como una expansión en la base del sitio.

\[| \psi (x) \rangle = \sum _ {n = 0}^{N - 1} c _ {n} ( \mathrm {x} ) | \varphi _ {n} \left( x - x _ {n} \right) \rangle \label{14.31}\]

que se escribe con el fin de señalar la dependencia de estas funciones de onda en el espaciamiento de celosía x, y la posición de una molécula particular en xn. Tal expansión debería funcionar bien cuando las interacciones electrónicas entre sitios son lo suficientemente débiles como para tratarlas de manera perturbadora. Para la estructura electrónica de los sólidos, esto se conoce como el modelo de unión estrecha, que describe la estructura de bandas como una combinación lineal de orbitales atómicos.

En lugar de diagonalizar al hamiltoniano, podemos aprovechar su simetría traslacional para obtener los autoestados. La simetría del hamiltoniano es tal que permanece inalterada por cualquier número integral de traducciones a lo largo de la cadena. Es decir, los resultados no se modifican para cualquier suma en la Ecuación\ ref {14.30} y\ ref {14.31} sobre enteros\(N\) consecutivos. De manera similar, la función de onda molecular en cualquier sitio no cambia por tal traducción. Escrito en términos de un operador de desplazamiento\(D = e^{i p _ {x} \alpha / \hbar}\) que desplaza la función de onda molecular en una constante de celosía

\[| \varphi ( x + n \alpha ) \rangle = D^{n} | \varphi (x) \rangle \label{14.32}\]

Estas observaciones subyacen al teorema de Bloch, que establece que los estados propios de un sistema periódico variarán solo por un desplazamiento de fase cuando son desplazados por una constante de celosía.

\[| \psi ( x + \alpha ) \rangle = e^{i k \alpha} | \psi (x) \rangle \label{14.33}\]

Aquí\(k\) está el vector de ondas, o vector reticular recíproco, una cantidad real. Así, los coeficientes de expansión en la Ecuación\ ref {14.31} tendrán una amplitud que refleje una excitación extendida por igual entre los N sitios, y solo varían entre sitios por un factor de fase espacialmente variable. Equivalentemente, se espera que los autoestados tengan una forma que sea producto de un factor de fase espacialmente variable y una función periódica:

\[| \psi (x) \rangle = e^{i k x} u (x) \label{14.34}\]

Estos factores de fase están estrechamente relacionados con los operadores de desplazamiento de celosía. Si la cadena lineal tiene\(N\) moléculas, los estados propios deben permanecer sin cambios con una traducción por la longitud de la cadena\(L = \alpha N\):

\[| \psi \left( x _ {n} + L \right) \rangle = | \psi \left( x _ {n} \right) \rangle\]

Por lo tanto, vemos que nuestras funciones de onda deben satisfacer

\[ N k \alpha = 2 \pi m\label{14.35}\]

donde\(m\) es un número entero. Además, dado que hay\(N\) sitios en la cadena, las soluciones únicas a la Ecuación\ ref {14.35} requieren que solo\(m\) puedan tomar valores enteros\(N\) consecutivos. Al igual que el índice del sitio\(n\), no hay una opción única de\(m\). Reescribiendo la ecuación\ ref {14.35}, el vector de ondas es

\[k _ {m} = \frac {2 \pi} {\alpha} \frac {m} {N} \label{14.36}\]

Vemos que para una celosía de\(N\) sitio,\(m\) puede tomar los valores enteros\(N\) consecutivos, de manera que eso\(k_m\alpha\) varía en un\(2\pi\) rango de ángulos. El índice de ondas m marca los estados propios de un\(N\) excitón de una cadena\(N\) molecular. Por convención,\(k_m\) se elige de tal manera que

\[- \pi / \alpha < k _ {m} \leq \pi / \alpha.\]

Entonces los valores correspondientes de\(m\) son enteros de\(-N-1)/2\) a\(N-1/2\) si hay un número impar de sitios de celosía o\(-N-2)/2\) a\(N/2\) para un número par de sitios. Por ejemplo, una cadena de 20 moléculas tendría\(m = -9,\, -8,\, … 9,\,10\).

Estos hallazgos conducen a la forma general para los estados propios de m un excitón

\[| k _ {m} \rangle = \frac {1} {\sqrt {N}} \sum _ {n = 0}^{N - 1} e^{i n k _ {m} \alpha} | n \rangle \label{14.37}\]

El factor de\(\sqrt{N}\) asegura la correcta normalización de la función de onda,\(\langle \psi | \psi \rangle = 1\). Comparando la ecuación\ ref {14.37} y\ ref {14.31} vemos que los coeficientes de expansión para el n-ésimo sitio del m-ésimo estado propio es

\[c _ {m , n} = \frac {1} {\sqrt {N}} e^{i n k _ {m} \alpha} = \frac {1} {\sqrt {N}} e^{i 2 \pi n m / N} \label{14.38}\]

Vemos que para el estado\(| k _ {0} \rangle\), con\(m = 0\), el factor de fase es el mismo para todos los sitios. En otras palabras, los dipolos de transición de la cadena oscilarán en fase, sumando constructivamente para todos los sitios. Para el caso de que\(k _ {m} = \pi / \alpha\), vemos que cada sitio está desfasado con sus vecinos más cercanos. Mirando el caso del dímero,\(N = 2\), vemos eso\(m = 0\) o,\(k_m = 0\) o\(1\)\(\pi/2\), y recuperamos los autoestados simétricos y antisimétricos esperados:

\[| k _ {0} \rangle = \frac {1} {\sqrt {2}} \sum _ {n = 0}^{1} e^{i n 0} | n \rangle = \frac {1} {\sqrt {2}} ( | 0 \rangle + | 1 \rangle )\]

para\(k=0\) y

\[| k _ {1} \rangle = \frac {1} {\sqrt {2}} \sum _ {n = 0}^{1} e^{i n \pi} | n \rangle = \frac {1} {\sqrt {2}} ( | 0 \rangle - | 1 \rangle )\]

para\(k = \pi / \alpha\).

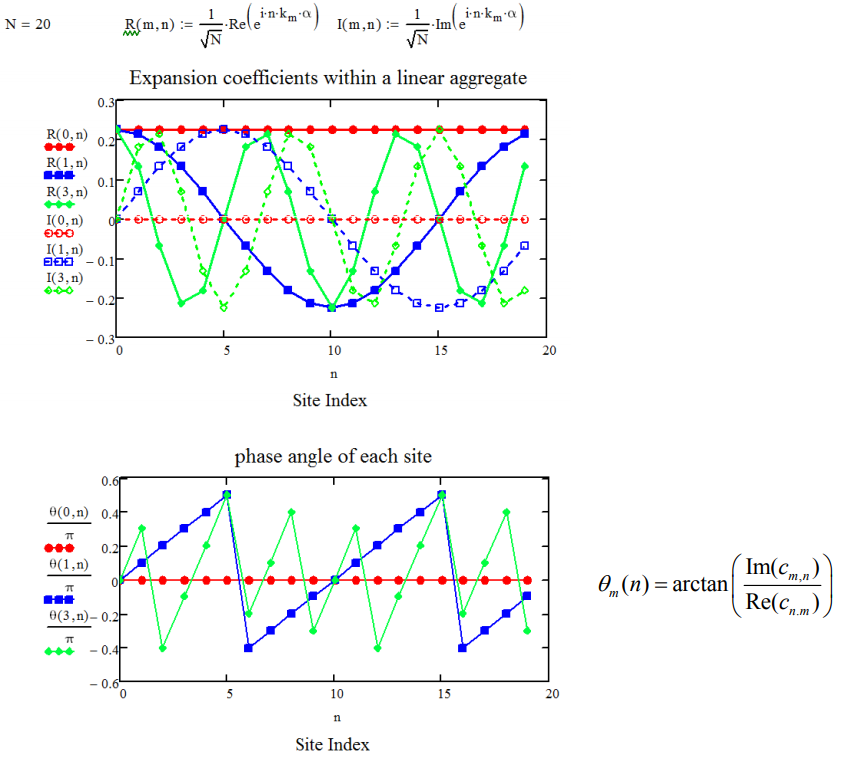
Esquemáticamente para\(N = 20\), vemos como la fase dipolo varía con\(k_m\), trazando los componentes reales e imaginarios de los coeficientes de expansión.

Además, podemos evaluar los elementos de la matriz dipolar de transición de un excitón\(M(k_m)\), los cuales se expresan como superposiciones de los momentos dipolares en cada sitio,\(\overline {\mu} _ {n}\):

\[\overline {M} = \sum _ {n = 0}^{N - 1} \overline {\mu} _ {n} \label{14.39}\]

\[\begin{align} M _ {m} = \left\langle k _ {m} | \overline {M} | G \right\rangle \\[4pt] = \frac {1} {\sqrt {N}} \sum _ {n = 0}^{N - 1} e^{i n k _ {n} \alpha} \left\langle n \left| \overline {\mu} _ {n} \right| G \right\rangle \label{14.40} \end{align}\]

La fase de los dipolos de transición de la cadena coincide con su fase dentro de cada estado k. Así, para nuestro problema, en el que todos los dipolos son paralelos, las transiciones del estado fundamental al\(k_m=0\) estado llevarán toda la fuerza del oscilador. A continuación se representa una ilustración de las relaciones de fase entre dipolos en una cadena con\(N = 20\).

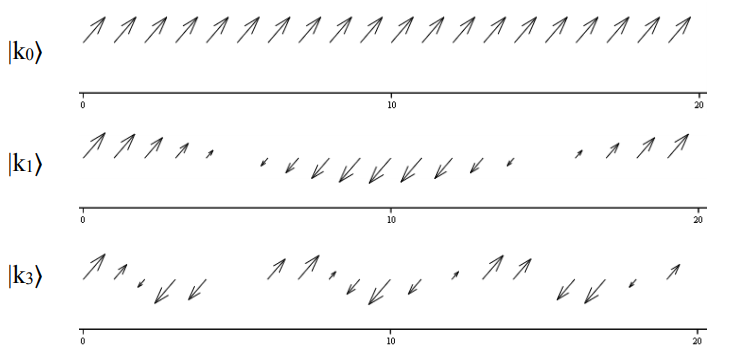
Finalmente, resolvamos para los valores propios de energía de un excitón calculando el valor de expectativa del operador hamiltoniano, Ecuación\ ref {14.30}

\[\begin{align} E \left( k _ {m} \right) &= \left\langle k \left| H _ {0} \right| k \right\rangle \\[4pt] &= \frac {1} {N} \sum _ {n , m = 0}^{N - 1} e^{i ( n - m ) k \alpha} \left\langle m \left| H _ {0} \right| n \right\rangle \label{14.41} \end{align} \]

\[\left\langle k _ {m} \left| H _ {S} \right| k _ {m} \right\rangle = \frac {1} {N} \sum _ {n = 0}^{N - 1} \varepsilon _ {0} = \varepsilon _ {0}\]

\[\begin{align} \left\langle k _ {m} | V | k _ {m} \right\rangle &= \frac {1} {N} \sum _ {n = 0}^{N - 1} \left\{e^{i k _ {m} \alpha} \langle n - 1 | V | n \rangle + e^{- i k _ {m} \alpha} \langle n + 1 | V | n \rangle \right\}\\[4pt] &= 2 J \cos \left( k _ {m} \alpha \right) \label{14.42} \end{align}\]

Predice que la banda de estados de un excitón varía en energía entre\(\varepsilon _ {0} - 2 J\) y\(\varepsilon _ {0} + 2 J\). Si tomamos J como negativo, como se esperaba para el caso de agregados J (acoplamientos negativos), entonces\(k = 0\) está en la parte inferior de la banda. A continuación se ilustran ejemplos para el\(N=20\) agregado.

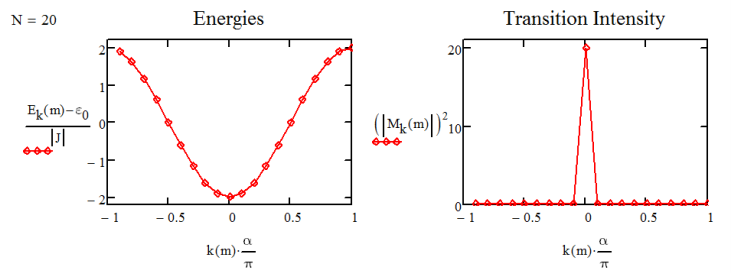
Tenga en cuenta que el resultado en la Ecuación\ ref {14.42} le da una división\(4J\) entre los dos estados del dímero, a diferencia de la\(2J\) división esperada de antes. Esto es resultado de las condiciones de frontera periódicas que aquí hacemos cumplir. Ahora estamos en condiciones de trazar el espectro de absorción para agregados, sumando sobre estados propios y asumiendo una forma de línea lorentziana para el sistema:

\[\sigma ( \omega ) = \sum _ {m} \left| M _ {m} \right|^{2} \frac {\Gamma^{2}} {\left( \hbar \omega - E \left( k _ {m} \right) \right) + \Gamma^{2}}\]

Para una cadena de osciladores 20 con acoplamiento negativo, el espectro se representa a continuación. Tenemos un pico correspondiente al modo k0 que alcanza su punto máximo\(\hbar \omega = \varepsilon _ {0} - 2 J\) y lleva la fuerza del oscilador de los 20 dipolos.

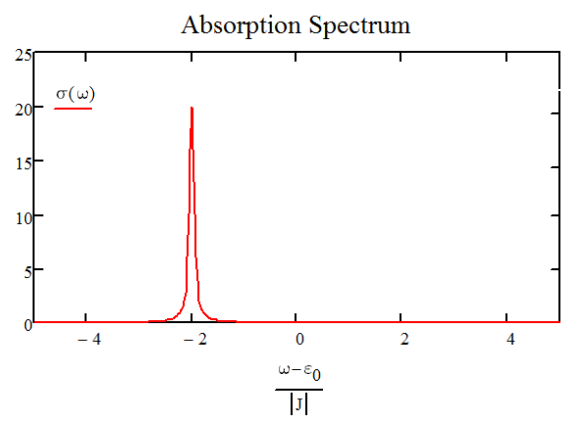
Espectro de absorción para\(N=20\) agregado con condiciones límite periódicas y\(J<0\).

Condiciones de contorno abierto

Aparecen tipos similares de soluciones sin usar condiciones de contorno periódicas. Para el caso de condiciones de límite abierto, en las moléculas al final de la cadena solo se acoplan al vecino más cercano de la cadena. En este caso, es útil etiquetar en los sitios de\(n = 1,2,...,N\). Además,\(m = 1,2,...,N\). Bajo esas condiciones, uno puede resolver para los autoestados usando el uso de la condición límite que\(\psi = 0\) en los sitios\(0\) y\(N+1\). El cambio en la condición de límite da soluciones sinusoidales:

\[| k _ {m} \rangle = \sqrt {\frac {2} {N + 1}} \sum _ {n = 1}^{N} \sin \left( \frac {\pi m n} {N + 1} \right) | n \rangle\]

Los valores propios de la energía son

\[E _ {m} = \omega _ {0} + 2 J \cos \left( \frac {\pi m} {N + 1} \right)\]

Espectro de absorción para N = 20 agregado con condiciones límite periódicas y\(J < 0\). Volviendo al caso del dímero (\(N=2\)), ahora podemos confirmar que recuperamos los autoestados simétricos y antisimétricos, con una división energética de\(2J\).

Si calcula la intensidad del oscilador para estas transiciones usando el operador dipolo en la Ecuación\ ref {14.39}, se encuentra:

\[M _ {m}^{2} = \left| \left\langle k _ {m} | \overline {M} | G \right\rangle \right|^{2} = \left( \frac {1 - ( - 1 )^{m}} {2} \right)^{2} \frac {2 \mu^{2}} {N + 1} \cot^{2} \left( \frac {\pi m} {2 ( N + 1 )} \right) \]

Este resultado muestra que la mayor parte de la fuerza del oscilador radica en el\(m =1\) estado, para el cual todos los osciladores están en fase. Para grandes\(N\),\(M_1^2\) lleva 81% de la fuerza del oscilador, con aproximadamente 9% en la transición al\(m = 3\) estado.

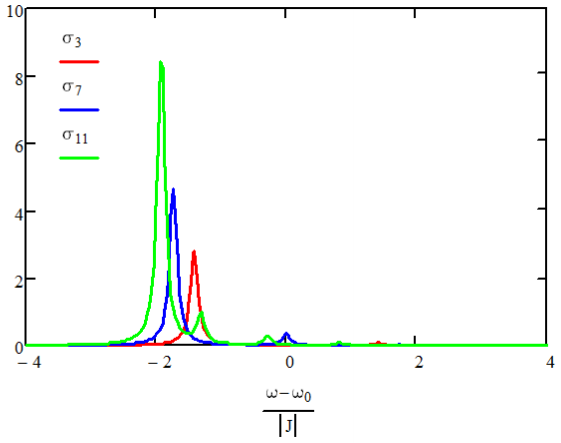
Espectros de absorción\(N=3,7,11\) para acoplamiento negativo.

El desplazamiento en el pico de la absorción con respecto al monómero da el acoplamiento\(J\). Incluir interacciones de largo alcance tiene el efecto de desplazar la banda de excitones asimétricamente alrededor\(\omega _ {0}\).

• \(\Omega _ {1} = \omega _ {0} + 2.4 J\)(\(m=1\), parte inferior de la banda con\(J\) negativo)
• \(\Omega _ {N} = \omega _ {0} - 1.8 J\)(Parte superior de la banda)

Estrechamiento de la Bolsa

Si la cadena no es homogénea, es decir, todas las moléculas no tienen la misma energía de sitio\(\varepsilon _ {0}\), entonces podemos modelar este efecto como trastorno aleatorio gaussiano. La energía de un sitio dado es

\[\varepsilon _ {n} = \varepsilon _ {0} + \delta \omega _ {n}\]

Agregamos como término extra a nuestro hamiltoniano anterior, Ecuación\ ref {14.30}, para dar cuenta de esta variación.

\[H _ {0} = H _ {s} + H _ {d i s} + V\]

\[H _ {d i s} = \sum _ {n} \delta \omega _ {n} | n \rangle \langle n |\]

El efecto es desplazar y mezclar los estados de excitón homogéneos. Espectros de absorción para N = 3,7,11 para acoplamiento negativo

\[\delta \Omega _ {k} = \left\langle k \left| H _ {d i s} \right| k \right\rangle = \frac {2} {N + 1} \sum _ {n} \sin^{2} \left( \frac {\pi k n} {N + 1} \right) \delta \omega _ {n}\]

Encontramos que estos cambios son también variables aleatorias gaussianas, con una desviación estándar de\(\Delta \sqrt {3 / 2 ( N + 1 )}\), donde\(\Delta\) está la desviación estándar para las energías del sitio. Entonces, la deslocalización del autoestado promedia el desorden sobre los\(N\) sitios, lo que reduce la distribución de energías por un factor escalando como\(N\). El estrechamiento de la línea de absorción con deslocalización se denomina estrechamiento de intercambio. Esto depende de que la distribución de las energías del sitio sea relativamente pequeña:\(\Delta \ll 3 \pi | J | / N^{3 / 2}\).

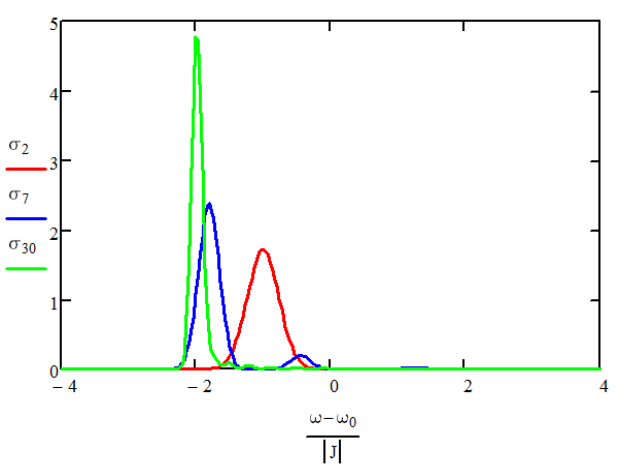
Espectros de absorción para\(N =2,6,30\) normalizados al número de osciladores. \(3\Delta = J\)y\(J<0\).

Lecturas

1. Knoester, J., Propiedades Ópticas de Agregados Moleculares. En Actas de la Escuela Internacional de Física “Enrico Fermi” Curso CXLIX, Agranovich, M.; La Rocca, G. C., Eds. IOS Press: Amsterdam, 2002; pp 149-186.