1.1: Procesos de Markov

Distribuciones y Transiciones de Probabilidad

Supongamos que un sistema arbitrario de interés puede estar en cualquiera de estados\(N\) distintos. El sistema podría ser una proteína que explora diferentes estados conformacionales; o un par de moléculas que oscilan entre un estado de “reactivos” y un estado de “productos”; o cualquier sistema que pueda muestrear diferentes estados a lo largo del tiempo. Tenga en cuenta aquí que\(N\) es finito, es decir, los estados disponibles son discretizados. En general, podríamos considerar sistemas con un conjunto continuo de estados disponibles (y lo haremos en la sección 1.3), pero por ahora nos limitaremos al caso de un número finito de estados disponibles. De acuerdo con nuestro esquema de discretización, también consideraremos (de nuevo, por ahora) la evolución temporal del sistema en términos de tiempos discretos en lugar de una variable de tiempo continua.

Que el sistema esté en algún estado desconocido\(m\) en el timesteep\(s\), y supongamos que estamos interesados en la probabilidad de encontrar el sistema en un estado específico\(n\), posiblemente pero no necesariamente el mismo que state\(m\), en el siguiente timesteep \(s+1\). Vamos a denotar esta probabilidad por

\[P(n, s+1)\]

Si tuviéramos conocimiento de ello\(m\), entonces esta probabilidad podría describirse como la probabilidad de que el sistema esté en estado\(n\) en el timesteep\(s+1\) dado que el sistema estaba en estado\(m\) en el timesteep\(s\). Las probabilidades de esta forma se conocen como probabilidades condicionales, y denotaremos esta probabilidad condicional por

\[Q(m, s \mid n, s+1)\]

En muchas situaciones de interés físico, la probabilidad de una transición de estado\(m\) a estado\(n\) es independiente del tiempo, dependiendo solo de la naturaleza de\(m\) y\(n\), y así dejamos caer los argumentos timestep para simplificar la notación,

\[Q(m, s \mid n, s+1) \equiv Q(m, n)\]

Esta observación puede parecer contradictoria, porque nos interesa la probabilidad dependiente del tiempo de observar un sistema en un estado\(n\) al tiempo que afirmamos que la probabilidad de transición descrita anteriormente es independiente del tiempo. Pero aquí no hay contradicción, porque la probabilidad de transición\(Q\) -una probabilidad condicional- es una cantidad diferente de la probabilidad dependiente del tiempo\(P\) que nos interesa. De hecho, podemos expresar\(P(n, s+1)\) en términos\(Q(m, n)\) y otras cantidades de la siguiente manera:

Como no conocemos el estado actual\(m\) del sistema, consideramos todos los estados posibles\(m\) y multiplicamos la probabilidad de que el sistema esté en estado en el\(m\) momento del cambio\(s\) por la probabilidad de que el sistema esté en estado \(n\)en timestep\(s+1\) dado que está en estado\(m\) en timestep\(s\). La suma de todos los estados posibles\(m\) da\(P\left(n, s_{1}\right)\) en el timesteep\(s+1\) en términos de las probabilidades correspondientes en el timesteep\(s\).

Matemáticamente, esta formulación dice

\[P(n, s+1)=\sum_{m} P(m, s) Q(m, n)\]

Hemos avanzado algo hacia un método práctico de hallazgo\(P(n, s+1)\), pero la formulación actual Ec. (1.1) requiere el conocimiento tanto de las probabilidades de transición como de\(Q(m, n)\) las probabilidades\(P(m, s)\) para todos los estados\(m\). Desafortunadamente,\(P(m, s)\) es tanto un misterio para nosotros como\(P(n, s+1)\). Lo que solemos conocer y controlar en los experimentos son las condiciones iniciales; es decir, si preparamos el sistema en estado\(k\) en el timestep\(s=0\), entonces lo sabemos\(P(k, 0)=1\) y\(P(n, 0)=0\) para todos\(n \neq k\). Entonces, ¿cómo nos expresamos\(P(n, s+1)\) en términos de las condiciones iniciales del experimento?

Podemos proceder inductivamente: si podemos escribir\(P(n, s+1)\) en términos de\(P(m, s)\), entonces también podemos escribir\(P(m, s)\) en términos de\(P(l, s-1)\) por el mismo enfoque:

\[P(n, s+1)=\sum_{l, m} P(l, s-1) Q(l, m) Q(m, n)\]

Tenga en cuenta que\(Q\) tiene dos parámetros, cada uno de los cuales puede tomar valores\(N\) posibles. En consecuencia, podemos optar por escribir\(Q\) como una\(N \times N\) matriz\(\mathbf{Q}\) con elementos de matriz\((\mathbf{Q})_{m n}=Q(m, n)\). Reordenando las sumas en la Ec. (1.2) de la siguiente manera,

\[P(n, s+1)=\sum_{l} P(l, s-1) \sum_{m} Q(l, m) Q(m, n)\]

reconocemos la suma\(m\) como la definición de un producto matriz,

\[\sum_{m}(\mathbf{Q})_{l m}(\mathbf{Q})_{m n}=\left(\mathbf{Q}^{2}\right)_{l n}\]

Por lo tanto, la Ec. (1.2) se puede refundar como

\[P(n, s+1)=\sum_{l} P(l, s-1)\left(\mathbf{Q}^{2}\right)_{l n}\]

Este proceso se puede continuar inductivamente hasta que\(P(n, s+1)\) se escriba completamente en términos de condiciones iniciales. El resultado final es:

\[\begin{aligned} P(n, s+1) &=\sum_{m} P(m, 0)\left(\mathbf{Q}^{s+1}\right)_{m n} \\ &=P(k, 0)\left(\mathbf{Q}^{s+1}\right)_{m n} \end{aligned}\]

donde\(k\) está el estado inicial conocido del sistema (todos los demás\(m\) no contribuyen a la suma ya que\(P(m, 0)=0\) para\(m \neq k\)). Cualquier proceso que pueda describirse de esta manera se denomina proceso de Markov, y la secuencia de eventos que comprende el proceso se llama cadena de Markov.

Una discusión más rigurosa sobre los orígenes y la naturaleza de los procesos de Markov se puede encontrar en, por ejemplo, de Groot y Mazur [2].

La matriz de probabilidad de transición

Ahora consideramos algunas propiedades importantes de la matriz de probabilidad de transición\(\mathbf{Q}\). En virtud de su definición, no\(Q\) es necesariamente hermitiana: si fuera hermitiana, toda transición concebible entre estados tendría que tener la misma probabilidad hacia adelante y hacia atrás, lo que muchas veces no es el caso.

Ejemplo: Considerar un sistema químico que pueda existir ya sea en un estado reactivo A o en un estado de producto B, con probabilidad de reacción directa\(p\) y probabilidad de reacción hacia atrás\(q=1-p\),

\[\mathrm{A} \underset{q}{\stackrel{p}{\rightleftharpoons}} \mathrm{B}\]

La matriz de probabilidad de transición\(\mathbf{Q}\) para este sistema es la\(2 \times 2\) matriz

\[\mathbf{Q}=\left(\begin{array}{ll} q & p \\ q & p \end{array}\right)\]

Para construir esta matriz, primero observamos que las probabilidades dadas describen directamente los elementos fuera de la diagonal\(Q_{A B}\) y\(Q_{B A}\) luego invocamos la conservación de la probabilidad. Por ejemplo, si el sistema está en estado reactivo\(A\), solo puede permanecer\(A\) o reaccionar para formar el producto\(B\); no hay otros resultados posibles, por lo que debemos tener\(Q_{A A}+Q_{A B}=1 .\) Esto fuerza el valor\(1-p=q\) sobre \(Q_{A A}\), y un argumento similar arroja\(Q_{B B}\).

Claramente esta matriz no es simétrica, de ahí que tampoco sea hermitiana, demostrando así nuestra primera observación general al respecto\(\mathbf{Q}\).

La no hermiticidad de\(\mathbf{Q}\) implica también que sus valores propios no\(\lambda_{i}\) son necesariamente de valor real. Sin embargo,\(\mathbf{Q}\) produce dos conjuntos de vectores propios, un conjunto izquierdo\(\chi_{i}\) y un conjunto derecho\(\phi_{i}\), que satisfacen las relaciones

\[\begin{aligned} &\chi_{i} \mathbf{Q}=\lambda_{i} \chi_{i} \\ &\mathbf{Q} \phi_{i}=\lambda_{i} \phi_{i} \end{aligned}\]

Los vectores propios izquierdo y derecho de\(\mathbf{Q}\) son ortonormales,

\[\left\langle\chi_{i} \mid \phi_{j}\right\rangle=\delta_{i j}\]

y forman un conjunto completo, de ahí que haya una resolución de la identidad del formulario

\[\sum_{i}\left|\phi_{i}\right\rangle\left\langle\chi_{i}\right|=1\]

La conservación de la probabilidad restringe aún más los elementos de\(\mathbf{Q}\) no ser negativos con\(\sum_{n} \mathbf{Q}_{m n}=1\). Se puede demostrar que esta condición garantiza que todos los valores propios de\(\mathbf{Q}\) están delimitados por el círculo unitario en el plano complejo,

\[\left|\lambda_{i}\right| \leq 1, \forall i\]

Comprobante de la Ec. (1.12): El\(i^{\text {th }}\) valor propio de\(\mathrm{Q}\) satisface

\[\lambda_{i} \phi_{i}(n)=\sum_{m} Q_{n m} \phi_{i}(m)\]

para cada uno\(n\). Tomemos el valor absoluto de esta relación,

\[\left|\lambda_{i} \phi_{i}(n)\right|=\left|\sum_{m} Q_{n m} \phi_{i}(m)\right|\]

Ahora podemos aplicar la desigualdad triangular al lado derecho de la ecuación:

\[\left|\sum_{m} Q_{n m} \phi_{i}(m)\right| \leq \sum_{m}\left|Q_{n m} \phi_{i}(m)\right|\]

Además, dado que todos los elementos de no\(\mathbf{Q}\) son negativos,

\[\left|\lambda_{i} \phi_{i}(n)\right| \leq \sum_{m} Q_{n m}\left|\phi_{i}(m)\right|\]

Ahora bien, los\(\phi_{i}(n)\) son finitos, por lo que debe haber alguna constante\(c\) tal que

\[\left|\phi_{i}(n)\right| \leq c\]

para todos\(n\). Entonces nuestra relación de desigualdad triangular dice

\[c\left|\lambda_{i}\right| \leq c \sum_{m} Q_{n m}\]

Por último\(\sum_{m} Q_{n m}=1\), ya que, tenemos el resultado deseado,

\[\left|\lambda_{i}\right| \leq 1\]

Otra característica clave de la matriz de probabilidad de transición\(\mathbf{Q}\) es la siguiente afirmación, que está íntimamente relacionada con la noción de estado de equilibrio:

\[\text { Q always has the eigenvalue } \lambda=1\]

Prueba de la Ec. (1.13): Nos referimos ahora a los vectores propios\(\mathbf{Q}:\) izquierdos de un vector propio izquierdo dado\(\chi_{i}\) satisface

\[\chi_{i}(n) \lambda_{i}=\sum_{m} \chi_{i}(m) Q_{m n}\]

Resumiendo\(n\), encontramos

\[\sum_{n} \chi_{i}(n) \lambda_{i}=\sum_{n} \sum_{m} \chi_{i}(m) Q_{m n}=\sum_{m} \chi_{i}(m)\]

ya que\(\sum_{m} Q_{n m}=1\). Así, tenemos la siguiente ecuación secular:

\[\left(\lambda_{i}-1\right) \sum_{n} \chi_{i}(n)=0\]

Claramente,\(\lambda=1\) es uno de los valores propios que satisface esta ecuación.

La descomposición de la ecuación secular en la prueba anterior tiene una interpretación física directa: el valor propio\(\lambda_{1}=1\) tiene un vector propio correspondiente que satisface\(\sum_{n} \chi_{1}(n)=1\); esta solución propia de estado estacionario corresponde al estado estacionario de un sistema \(\chi_{1}(n)=P_{\mathrm{st}}(n)\). Entonces se deduce de la condición de normalización que\(\phi_{1}(n)=1\). Los valores propios restantes satisfacen\(\left|\lambda_{j}\right|<1\) cada uno\(\sum_{n} \chi_{j}(n)=0\) y por lo tanto corresponden a fluctuaciones de suma cero sobre el estado de equilibrio.

A la luz de estas propiedades de\(\mathbf{Q}\), podemos definir la evolución dependiente del tiempo de un sistema en términos de los autoestados de\(\mathbf{Q}\); esta representación se denomina la descomposición espectral de\(P(n, s)\) (el conjunto de valores propios de una matriz también se conoce como el espectro de esa matriz). En base a los vectores propios izquierdo y derecho de\(\mathbf{Q}\), la probabilidad de estar en estado\(n\) en el timesteep\(s\), dado el estado inicial como\(n_{0}\), es

\[P(n, s)=\left\langle n_{0}\left|\mathbf{Q}^{s}\right| n\right\rangle=\sum_{i}\left\langle n_{0} \mid \phi_{i}\right\rangle \lambda_{i}^{s}\left\langle\chi_{i} \mid n\right\rangle\]

Si asignamos (arbitrariamente) el estado estacionario a\(i=1\), tenemos\(\lambda_{1}=1\) y\(\chi_{1}=P_{s t}\), donde\(P_{s t}\) está la distribución de probabilidad de estado estacionario o equilibrio. Por lo tanto,

\[P(n, s)=P_{s t}(n)+\sum_{i \neq 1} \phi_{i}\left(n_{0}\right) \lambda_{i}^{s} \chi_{i}(n)\]

La descomposición espectral demuestra ser bastante útil en el análisis de distribuciones de probabilidad más complicadas, especialmente aquellas que tienen suficientes estados como para requerir análisis computacional.

Ejemplo: Consideremos un sistema que tenga tres estados con probabilidades de transición como se ilustra en la Figura 1.1. Observe que las transiciones en sentido antihorario y en sentido horario tienen diferentes probabilidades, lo que permite que este sistema exhiba una corriente o flujo neto. También, supongamos\(p+q=1\) que para que el sistema deba conmutar estados en cada momentosetep.

Figura 1.1: Un sistema simple de tres estados con flujo distinto de cero

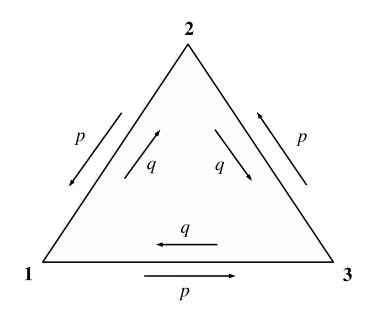
La matriz de probabilidad de transición para este sistema es

\[\mathbf{Q}=\left(\begin{array}{lll} 0 & p & q \\ q & 0 & p \\ p & q & 0 \end{array}\right)\]

Para determinar\(P(s)\), encontramos los valores propios y vectores propios de esta matriz y utilizamos la descomposición espectral, Ec. (1.14). La ecuación secular es

\[\operatorname{Det}(\mathbf{Q}-\lambda \mathbf{I})=\mathbf{0}\]

y sus raíces son

\[\lambda_{1}=1, \quad \lambda_{\pm}=-\frac{1}{2} \pm \frac{1}{2} \sqrt{3(4 p q-1)}\]

Observe que los valores propios de no equilibrio son complejos a menos que\(p=q=\frac{1}{2}\), lo que corresponde al caso de fuga del flujo neto. Si hay un flujo neto, estos valores propios complejos introducen un comportamiento oscilatorio a\(P(s)\).

En el caso especial\(p=q=\frac{1}{2}\), la matriz\(\mathbf{Q}\) es simétrica, por lo que los vectores propios izquierdo y derecho son idénticos,

\[\begin{aligned} \chi_{1} &=\phi_{1}^{T}=\frac{1}{\sqrt{3}}(1,1,1) \\ \chi_{2} &=\phi_{2}^{T}=\frac{1}{\sqrt{6}}(1,1,-2) \\ \chi_{3} &=\phi_{3}^{T}=\frac{1}{\sqrt{2}}(1,-1,0) \end{aligned}\]

donde\(T\) denota transposición. Supongamos que el estado inicial se da como estado 1, y nos interesa la probabilidad de estar en el estado 3 en el timesteep\(s, P_{1 \rightarrow 3}(s)\). Según la fórmula de descomposición espectral\(\mathrm{Eq} \cdot(1.14)\)

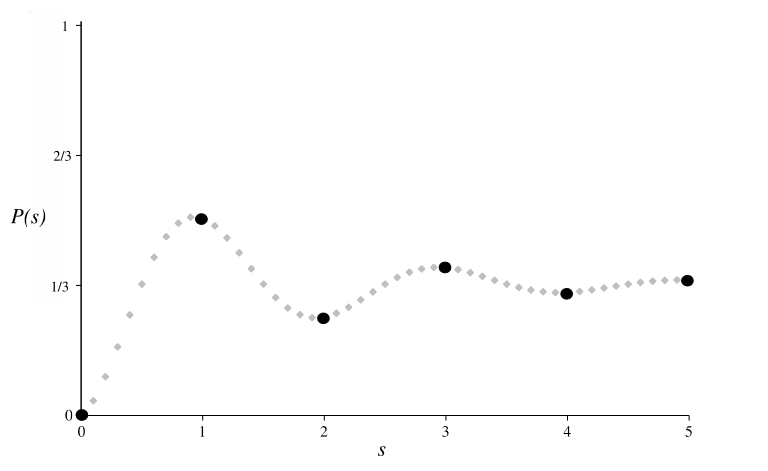
\[\begin{aligned} P_{1 \rightarrow 3}(s)=& \sum_{i} \phi_{i}(1) \lambda_{i}^{s} \chi_{i}(3) \\ =&\left(\frac{1}{\sqrt{3}}\right)\left(1^{s}\right)\left(\frac{1}{\sqrt{3}}\right) \\ &+\left(\frac{1}{\sqrt{6}}\right)(1)\left(-\frac{1}{2}\right)^{s}\left(\frac{1}{\sqrt{6}}\right)(-2) \\ &+\left(\frac{1}{\sqrt{2}}\right)(1)\left(-\frac{1}{2}\right)^{s}\left(\frac{1}{\sqrt{2}}\right)(0) \\ P_{1 \rightarrow 3}(s)=& \frac{1}{3}-\frac{1}{3}\left(-\frac{1}{2}\right)^{s} \end{aligned}\]

Obsérvese que en la evaluación de cada término se\(\phi\) utilizó el primer elemento de cada vector propio izquierdo\(\chi\) y el tercer elemento de cada vector propio derecho, ya que nos interesa la transición del estado 1 al estado 3. La figura\(1.2\) es una gráfica de\(P_{1 \rightarrow 3}(s)\); muestra que la probabilidad oscila alrededor del valor de equilibrio de\(\frac{1}{3}\), acercándose al valor de equilibrio asintóticamente.

Figura 1.2: Probabilidad de una transición del estado 1 al estado 3 frente al número de tiempos. Los puntos negros corresponden a los tiempos reales; los puntos grises se han interpolado para enfatizar la naturaleza oscilatoria de\(P(s)\).

Saldo Detallado

Nuestro último tema de consideración dentro del tema de los procesos de Markov es la noción de equilibrio detallado, que probablemente ya sea algo familiar a partir de la cinética elemental. Formalmente, un proceso de Markov con matriz de probabilidad de transición\(\mathbf{Q}\) satisface el balance detallado si se mantiene la siguiente condición:

\[P_{\mathrm{st}}(n) Q_{n m}=P_{\mathrm{st}}(m) Q_{m n}\]

Y este estado estacionario define la distribución de equilibrio:

\[P_{\mathrm{eq}}(n)=P_{\mathrm{st}}(n)=\lim _{t \rightarrow \infty} P(n, t)\]

Esta relación generaliza la noción de equilibrio detallado a partir de la cinética simple de que las tasas de procesos hacia adelante y hacia atrás en equilibrio deben ser iguales: aquí, en lugar de considerar solo un estado reactivo y un estado producto, requerimos que todos los pares de estados estén relacionados por la Ec. (1.16).

Obsérvese también que esta condición de equilibrio detallado es más general que simplemente exigir que\(\mathbf{Q}\) sea simétrica, ya que la definición más simple de la cinética elemental implicaría. Sin embargo, si un sistema obedece a un balance detallado, podemos describirlo usando una matriz simétrica a través de la siguiente transformación: let

\[V_{n m}=\frac{\sqrt{P_{\mathrm{st}}(n)}}{\sqrt{P_{\mathrm{st}}(m)}} Q_{n m}\]

Si hacemos la sustitución\(P(n, s)=\sqrt{P_{\mathrm{st}}(n)} \cdot \tilde{P}(n, s)\), alguna manipulación usando las ecuaciones (1.1) y (1.17) rinde

\[\frac{d \tilde{P}(n, t)}{d t}=\sum_{m} \tilde{P}(m, t) V_{m n}\]

La derivada\(\frac{d \tilde{P}(n, s)}{d t}\) aquí es realmente la diferencia finita\(\tilde{P}(n, s+1)-\tilde{P}(n, s)\) ya que estamos considerando procesos Markov de tiempo discreto, pero hemos introducido la notación derivada para comparar esta fórmula con resultados posteriores para sistemas de tiempo continuo.

Como hicimos para\(\mathbf{Q}\), podemos configurar un sistema propio para\(\mathbf{V}\), que produce una descomposición espectral similar a la de\(\mathbf{Q}\) con la excepción de que los vectores propios izquierdo y derecho\(\psi\) de\(\mathbf{V}\) son idénticos ya que \(\mathbf{V}\)es simétrico; en otras palabras,\(\left\langle\psi_{i} \mid \psi_{j}\right\rangle=\delta_{i j}\). Además, se puede demostrar que todos los valores propios que no corresponden al estado de equilibrio son negativos o cero; en particular, son reales. Los vectores propios de\(\mathbf{V}\) están relacionados con los vectores propios izquierdo y derecho de\(\mathbf{Q}\) by

\[\left|\phi_{i}\right\rangle=\frac{1}{\sqrt{P_{\mathrm{st}}}}\left|\psi_{i}\right\rangle \quad \text { and } \quad\left\langle\chi_{i}\right|=\sqrt{P_{\mathrm{st}}}\left\langle\psi_{i}\right|\]

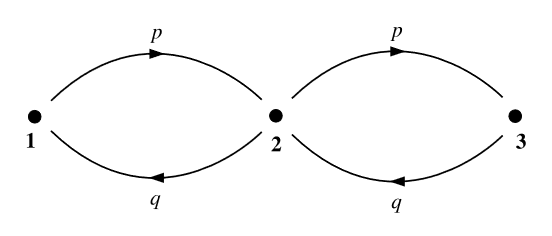
Ejemplo: Nuestro modelo final de sistema Markovic es una cadena lineal de tres estados (Figura 1.3) en la que el sistema debe pasar por el estado medio para poder llegar de cualquier extremo de la cadena al otro. Nuevamente lo requerimos\(p+q=1\). A partir de esta información, podemos construir\(\mathbf{Q}\),

\[\mathbf{Q}=\left(\begin{array}{ccc} q & p & 0 \\ q & 0 & p \\ 0 & q & p \end{array}\right)\]

Observe cómo la diferencia entre la cadena lineal de tres sitios y el anillo de tres sitios del ejemplo anterior se manifiesta en la estructura de\(\mathbf{Q}\), particularmente en la dirección de la diagonal cero. Esta diferencia estructural se traslada a cadenas y anillos de\(N\) sitio general.

Para determinar la distribución de probabilidad de equilibrio\(P_{\text {st }}\) para este sistema, uno podría multiplicarse\(\mathbf{Q}\) por sí mismo muchas veces y esperar encontrar una fórmula analítica para\(\lim _{s \rightarrow \infty} \mathbf{Q}^{s} ;\) sin embargo, un enfoque menos tedioso e intuitivo es el siguiente:

Al notar que el sistema no puede permanecer en el estado 2 a la vez\(s\) si ya está en el estado 2 a la vez\(s-1\), concluimos que\(P(1, s+2)\) depende sólo de\(P(1, s)\) y\(P(3, s)\). También, las probabilidades condicionales\(P(1, s+2 \mid 1, s)\) y\(P(1, s+2 \mid 3, s)\) son ambas iguales a\(q^{2}\). Asimismo,\(P(3, s+2 \mid 1, s)\) y ambos\(P(3, s+2 \mid 3, s)\) son iguales a\(p^{2} .\) Finalmente, si el sistema está en el estado 2 en el momento\(s\), solo puede volver al estado 2 en el momento pasando\(s+2\) por el estado 1 o el estado 3 en el momento \(s+1\). La probabilidad de cualquiera de estas ocurrencias es\(p q\).

Figura 1.3: Un sistema de tres estados en el que los sitios ya no son idénticos

Entonces la relación\(P_{\mathrm{st}}(1): P_{\mathrm{st}}(2): P_{\mathrm{st}}(3)\) en el límite de equilibrio es\(q^{2}: q p: p^{2}\). Simplemente tenemos que normalizar estas probabilidades señalando eso\(q^{2}+q p+p^{2}=(q+p)^{2}-q p=1-q p\). Así, la distribución de equilibrio es

\[P(s)=\frac{1}{1-q p}\left(q^{2}, q p, p^{2}\right)\]

Al enchufar cada par de estados a la condición de balance detallado, verificamos que este sistema satisface el balance detallado y, por lo tanto, todos sus valores propios son reales, aunque\(\mathbf{Q}\) no sean simétricos.