1.2: Ecuaciones Maestras

Motivación y Derivación

Las técnicas desarrolladas en la teoría básica de los procesos de Markov son ampliamente aplicables, pero por supuesto hay muchos casos en los que la discretización del tiempo es inconveniente o completamente antifísica. En tales casos, una ecuación maestra (más humildemente denominada ecuación de tasa) puede proporcionar una descripción en tiempo continuo del sistema que esté en consonancia con todos nuestros resultados sobre procesos estocásticos.

Figura 1.4: Celosía infinita con velocidad de transición\(k\) entre todos los estados contiguos

Eq. \((1.22)\)es una ecuación maestra. Como sugiere la derivación,\(\mathbf{W}\) juega el papel de una matriz de probabilidad de transición en esta formulación. Puede notar que la ecuación maestra se ve estructuralmente muy similar a las ecuaciones de tasa en la cinética elemental; de hecho, la ecuación maestra es una generalización de tales ecuaciones de tasa, y la derivación anterior proporciona alguna justificación formal para las reglas que aprendemos en cinética para escribirlas. La matriz\(\mathbf{W}\) es análoga al conjunto de constantes de velocidad que indican las velocidades de reacción relativas entre especies en el sistema, y las probabilidades\(P_{n}\) son análogas a las concentraciones relativas de estas especies.

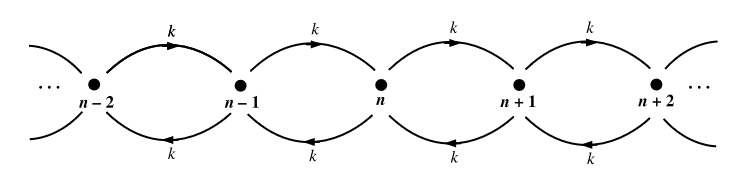
Ejemplo: Considera una caminata aleatoria sobre una celosía infinita unidimensional (ver Figura 1.4). Como se indica en la figura, la probabilidad de transición entre un punto de celosía y cualquiera de los puntos de celosía adyacentes es\(k\), y todas las demás probabilidades de transición son cero (en otras palabras, el sistema no puede “saltarse” sobre un punto de celosía sin ocuparlo primero). Podemos escribir una ecuación maestra para describir el flujo de probabilidad entre los sitios de celosía de una manera análoga a escribir una ley de tasa. Para cualquier sitio dado\(n\) en la celosía, la probabilidad puede fluir\(n\) desde cualquier sitio\(n-1\) o sitio\(n+1\), y ambos ocurren a la velocidad\(k\); asimismo, la probabilidad puede fluir fuera del estado\(n\) a cualquier sitio\(n+1\) o sitio\(n-1\), ambos de los cuales también ocurren a ritmo\(k\). Por lo tanto, la ecuación maestra para todos los sitios\(n\) en la celosía es

\[\dot{P}_{n}=k\left(P_{n+1}+P_{n-1}-2 P_{n}\right)\]

Ahora definimos el sitio promedio de ocupación como una suma sobre todos los sitios, ponderada por la probabilidad de ocupación en cada sitio,

\[\bar{n}=\sum_{n=-\infty}^{\infty} n P_{n}(t)\]

Entonces podemos calcular, por ejemplo, cómo evoluciona este sitio promedio con el tiempo,

\[\sum_{n=-\infty}^{\infty} n \dot{P}_{n}(t)=\dot{\bar{n}}=0\]

De ahí que el sitio promedio de ocupación no cambie con el tiempo en este modelo, por lo que si elegimos la distribución inicial para satisfacer\(\bar{n}=0\), entonces este será siempre el sitio promedio de ocupación.

Sin embargo, el desplazamiento\(\bar{n}^{2}\) cuadrático medio no es constante; de acuerdo con nuestra interpretación física del modelo, el desplazamiento cuadrático medio aumenta con el tiempo. En particular,

\[\sum_{n=-\infty}^{\infty} n^{2} \dot{P}_{n}(t)=\dot{\bar{n}}^{2}=2 k\]

Si la distribución de probabilidad inicial es una función delta en el sitio\(0, P_{n}(0)=\delta_{0}\), entonces resulta que el análisis de Fourier proporciona una ruta hacia una expresión de forma cerrada para el límite de largo plazo de\(P_{n}(t)\):

\[\begin{aligned} P_{n}(t)=\frac{1}{2 \pi} \int_{0}^{2 \pi} e^{i n z} e^{-2 k(1-\cos z) t} d z \\ \lim _{t \rightarrow \infty} P_{n}(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i n z} e^{-2 D\left(\frac{z^{2}}{2}\right) t} d z \end{aligned}\]

\[\lim _{t \rightarrow \infty} P_{n}(t)=\sqrt{\frac{1}{4 \pi D t}} e^{-\frac{n^{2}}{4 D t}}\]

En las manipulaciones anteriores, hemos sustituido por\(k\) la constante de difusión\(D\), el límite de largo tiempo de la constante de velocidad (en este caso, las dos son idénticas). Así, la distribución de probabilidad para ocupar los diversos sitios se convierte en gaussiana en largos tiempos.

Tiempo Medio del Primer Pasaje

Una de las cantidades más útiles que podemos determinar a partir de la ecuación maestra para una caminata aleatoria es el tiempo promedio que tarda la caminata aleatoria en llegar a un sitio en particular\(n_{s}\) por primera vez. Esta cantidad, llamada el tiempo medio del primer paso, se puede determinar a través del siguiente truco: colocamos una condición de límite absorbente en\(n_{s}, P_{n_{s}}(t)=0\). Siempre que la caminata llega al sitio\(n_{s}\), se queda ahí para todos los tiempos posteriores. Luego se calcula la probabilidad de supervivencia\(S(t)\), es decir, la probabilidad de que el caminante aún no haya visitado\(n_{s}\) en el momento\(t\),

\[S(t)=\sum_{n \neq n_{s}} P_{n}(t)\]

El tiempo medio del primer paso corresponde\(\langle t\rangle\) entonces a la probabilidad de supervivencia promediada en el tiempo,

\[\langle t\rangle=\int_{0}^{\infty} S(t) d t\]

A veces es más conveniente escribir el tiempo medio del primer paso en términos de la densidad de probabilidad de llegar al sitio\(n_{s}\) en el momento\(t\). Esta cantidad se denota por\(f(t)\) y satisface

\[f(t)=-\frac{d S(t)}{d t}=\sum_{n \neq n_{s}} P_{n}(t) W_{n n_{s}}\]

En términos de\(f(t)\), el tiempo medio del primer paso viene dado por

\[\langle t\rangle=\int_{0}^{\infty} t f(t) d t\]

El tiempo medio del primer paso es una cantidad de interés en una serie de aplicaciones de investigación actuales. Las tasas de extinción de fluorescencia, transferencia de electrones y extinción de excitones pueden formularse en términos del tiempo medio de primer paso de un proceso estocástico.

Ejemplo: Calculemos el tiempo medio de primer paso del modelo de tres sitios introducido en la Figura\(1.1\), teniendo todas las tasas de transición el mismo valor\(k\). Supongamos que el sistema está preparado en el estado 1, y nos interesa conocer el tiempo medio de primer paso para el sitio 3. Aplicando la condición de límite absorbente en el sitio 3, derivamos las siguientes ecuaciones maestras:

\[\left\{\begin{array}{l} \dot{P}_{1}=-2 k P_{1}+k P_{2} \\ \dot{P}_{2}=k P_{1}-2 k P_{2} \\ \dot{P}_{3}=k P_{1}+k P_{2} \end{array}\right.\]

La matriz de transición\(\mathbf{W}\) correspondiente a este sistema tendría una columna cero ya que\(P_{3}\) no ocurre en el lado derecho de ninguna de estas ecuaciones; de ahí que el sumidero lleve a un valor propio cero que podemos ignorar. La submatriz relevante

\[\mathbf{W}_{1,2}=\left(\begin{array}{cc} -2 k & k \\ k & -2 k \end{array}\right)\]

tiene valores propios\(\lambda_{1}=-k, \lambda_{2}=-3 k\). Usando la fórmula de descomposición espectral, encontramos que la probabilidad de supervivencia es

\[S(t)=\sum_{i, n}\left\langle 1 \mid \psi_{i}\right\rangle e^{\lambda_{i} t}\left\langle\psi_{i} \mid n\right\rangle=e^{-k t}\]

Por lo tanto, la densidad de probabilidad previamente definida\(f(t)\) viene dada por\(f(t)=k e^{-k t}\), y el tiempo medio del primer paso para el sitio 3 es

\[\langle t\rangle=\frac{1}{k}\]