4.4: Tails de larga duración y teoría de acoplamiento de modos

EL PROBLEMA

Figura 4.4: Colisión no correlacionada de dos partículas en un fluido

donde el núcleo de memoria se relaciona con la constante de difusión a través de la relación de Einstein

\[\gamma=\frac{1}{m D \beta}\]

En 1967, Alder y Wainwright utilizaron simulaciones por computadora para calcular la función de correlación de velocidad de los gases de esfera dura [6]. Descubrieron que en largos tiempos,\(C(t)\) exhibe una decadencia de la ley de poder en lugar de una decadencia exponencial. Es decir,\(C(t)\) decae según\(t^{-\frac{3}{2}}\)

\[\lim _{t \rightarrow \infty} C(t) \propto \frac{1}{t^{\frac{3}{2}}}\]

Este es el famoso problema de cola desde hace mucho tiempo en la teoría cinética.

Efectos de memoria

La suposición fundamental subyacente al modelo de decaimiento exponencial de la función de correlación de velocidad es que las colisiones entre partículas en un gas de esfera dura diluida son independientes. Esto significa que después de cada colisión, una partícula perderá memoria de su velocidad original hasta que su movimiento se haya vuelto completamente aleatorio. Esta suposición conduce a la decadencia exponencial\(C(t)=v_{o}^{2} e^{-t / \tau_{\text {coll }}}\), donde\(\tau_{\text {coll }}=\frac{1}{\gamma}\) está el tiempo promedio de colisión.

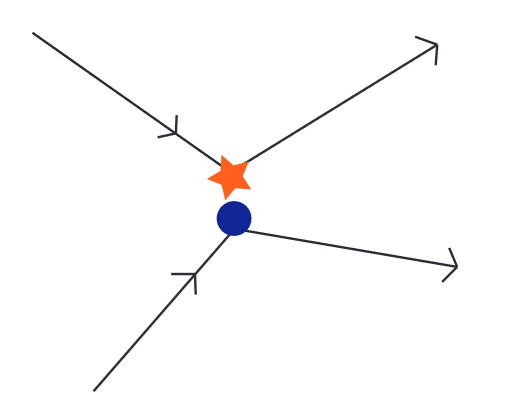
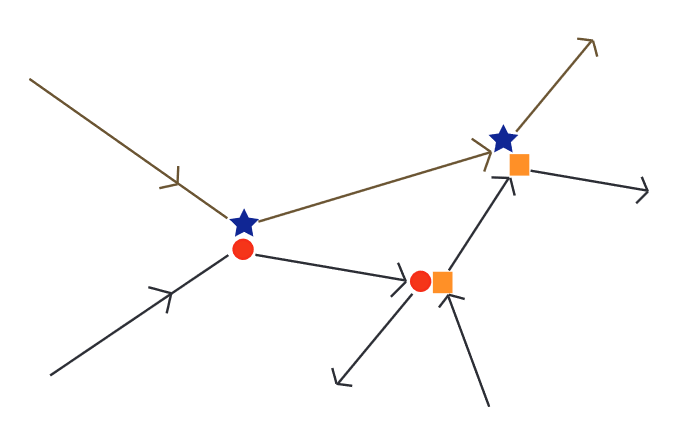
Sin embargo, también es posible que las colisiones no sean completamente independientes sino que estén correlacionadas. Se produciría una correlación si, por ejemplo, dos partículas chocan y luego chocan nuevamente después de sufrir algún número de otras colisiones (ver Figuras\(4.5\) y 4.6). Esto implica que hay una memoria a largo plazo en el sistema que conduciría a una decadencia que es más lenta que una exponencial.

Para estimar la forma de esta decadencia, podemos considerar la probabilidad de que, tras una colisión, una partícula permanezca en o regrese a su posición inicial después de un tiempo t,\(P(r=0, t)\). Para hacer una estimación aproximada de esta probabilidad, imagina que en cualquier momento podemos dibujar una “esfera de probabilidad” para la partícula. La probabilidad de encontrar la partícula dentro de la esfera es constante, y la probabilidad de encontrar la partícula fuera de la esfera es cero. En su momento\(t=0\), la partícula no ha tenido tiempo de alejarse de su posición inicial. Por lo tanto,\(P(r=0, t)=\delta(r)\). A medida que\(t\) aumenta, la partícula comienza a difundirse alejándose de su posición inicial. El radio de la esfera aumenta linealmente

Figura 4.5: Una partícula de prueba (estrella azul) colisiona con una partícula (círculo rojo), alterando la trayectoria de esa partícula de tal manera que colisiona con una tercera partícula (cuadrado amarillo). La posterior colisión de la tercera partícula con la partícula de prueba se correlaciona con la colisión inicial.

Figura 4.6: Los anillos de vórtice en el fluido alrededor de una partícula de esfera dura pueden contribuir a la cola de larga duración de la función de autocorrelación de velocidad [6]. con el tiempo según\(R=2 D^{2} t\), donde\(D\) está la constante de difusión.

Para estimar a\(P(r=0, t)\) partir de la esfera de probabilidad, tenga en cuenta que la probabilidad de encontrar la partícula en cualquier punto del espacio debe ser la unidad:

\[\int P(r, t) d r=1\]

Solo necesitamos integrarnos sobre el volumen de la esfera, ya que la probabilidad de encontrar la partícula en cualquier otro lugar es cero. Dentro de la esfera, la probabilidad es una constante,\(P(r, t)=P(t)\). Por lo tanto, esta integral simplifica

\[1=\int_{\text {sphere }} P(t) d r \propto V P(t)\]

El volumen de la esfera va como\(R^{d}=t^{\frac{d}{2}}\), donde\(d\) está la dimensión espacial. Por lo tanto, la probabilidad va como

\[P(r=0, t)=\frac{1}{V} \propto \frac{1}{R^{d}} \propto \frac{1}{t^{\frac{d}{2}}}\]

Para un sistema tridimensional, obtenemos un resultado consistente con las predicciones de Alder y Wainwright

\[P(r=0, t) \propto \frac{1}{t^{\frac{3}{2}}}\]

Esto demuestra que los efectos de memoria pueden ser la fuente de la decadencia de la ley de poder.

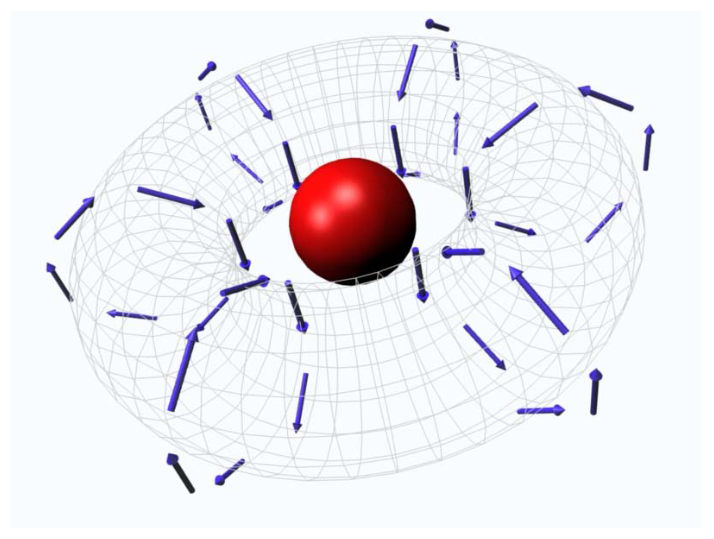
Podemos construir un modelo simple del comportamiento de un sistema para el cual los efectos de memoria son importantes. En este modelo, una partícula con una velocidad\(v_{o}\) crea un campo de velocidad a través de sus interacciones con otras partículas. Este campo de velocidad a su vez puede influir en el comportamiento a largo plazo de la partícula.

Podemos comenzar por obtener una estimación aproximada de este campo de velocidad a partir de la corriente transversal

\[J_{T}(k, t)=J_{T}(k, 0) e^{-\nu k^{2} t}\]

donde\(\nu=\frac{\eta}{m \rho}\) es la constante de difusión,\(\eta\) es la viscosidad de cizallamiento, y\(J_{T}(k, 0) \propto v_{o}\). La corriente transversal se escribe en\(k\) -espacio. Al transformar esto en espacio real, obtenemos una expresión para la disipación del campo de velocidad a lo largo del tiempo y el espacio

\[v(r, t) \propto \frac{v_{o}}{(\sqrt{4 \pi \nu t})^{3}} e^{\frac{-r^{2}}{2 \nu t}}\]

El campo de velocidad se disipa debido a la fricción. En tiempos cortos, la decadencia tiene una forma gaussiana. No obstante, en largos tiempos la decadencia está dominada por el prefactor, que va como\(\tau^{-\frac{3}{2}}\).

Modelo hidrodinámico

Una forma sencilla de derivar el resultado anterior sería evaluar la función de correlación de velocidad

\[C(t)=\langle v(t) v(0)\rangle\]

Usando el modelo hidrodinámico, podemos encontrar esta función de correlación tomando el promedio de equilibrio de la velocidad térmica promedio no en equilibrio

\[C(t)=\langle v(t) v(0)\rangle=\int d \vec{r}_{o} \frac{1}{V} \int d \vec{v}_{o} f_{B} v_{o}\langle v(t)\rangle_{\text {n.e. }}\]

donde\(f_{B}\) está la distribución de Boltzmann y\(\langle v(t)\rangle_{\text {n.e. }}\) es un campo de velocidad sin equilibrio:

\[\langle v(t)\rangle_{\text {n.e. }}=\frac{\left\langle v_{s}(t) \delta\left(v_{s}-v_{o}\right) \delta\left(r_{s}-r_{o}\right)\right\rangle}{\left\langle\delta\left(v_{s}-v_{o}\right) \delta\left(v_{s}-v_{o}\right) \delta\left(r_{s}-r_{o}\right)\right\rangle}\]

Aquí,\(s\) describe la partícula etiquetada.

El campo de velocidad de no equilibrio se puede representar como un acoplamiento de los modos lineales\(\rho^{s}\) y\(v_{s} .\)

\[\begin{aligned} \langle v(t)\rangle_{\text {n.e. }}=\int \rho^{s}(r, t) v_{s}(r, t) d r \\ =\frac{1}{\rho_{o}} \int \rho^{s}(r, t) J(r, t) d r \\ =\frac{\rho_{o}^{-1}}{(2 \pi)^{3}} \int \rho^{s}(k, t) J(k, t) d k \end{aligned}\]

Podemos resolver esto usando las soluciones de los modos hidrodinámicos:

\[\begin{aligned} \rho_{s}(k, t)=\rho_{s}(k, 0) e^{-k^{2} D t} \\ J_{\perp}(k, t)=J_{\perp}(k, 0) e^{-k^{2} \nu t} \\ J_{L}(k, t)=J_{L}(k, 0) e^{-k^{2} \frac{\Gamma}{2} t \pm i c_{s} k t} \end{aligned}\]

Para modos transversales,

\[\begin{aligned} v_{o}\langle v(t)\rangle_{\text {n.e. }}=\frac{1}{(2 \pi)^{3} \rho_{o}} \frac{2}{3} \int \rho^{s}(k, 0) e^{-k^{2} D t} J_{x}(k, 0) e^{-k^{2} \nu t} v_{x}^{s}(0) d k \\ =\frac{1}{(2 \pi)^{3} \rho_{o}} \frac{2}{3} \int \rho^{s}(k, 0) J_{x}(k, 0) v_{x}^{s}(0) e^{-k^{2}(D+\nu) t} d k \end{aligned}\]

Luego, toma el promedio de equilibrio

\[\left\langle\rho^{s}(k, 0) J_{x}(k, 0) v_{x}^{s}(0)\right\rangle=v_{o}^{2}\]

Por último,

\[\begin{aligned} C(t)=\frac{2}{3 \rho_{o}} v_{o}^{2} \frac{1}{(2 \pi)^{3}} \int d \vec{k} e^{-k^{2}(D+\nu) t} \\ =\frac{v_{o}^{2}}{12 \rho_{o}} \frac{1}{[\pi t(D+\nu)]^{\frac{3}{2}}} \\ \propto \frac{1}{t^{\frac{3}{2}}} \end{aligned}\]

Teoría del acoplamiento de modos

Como se muestra anteriormente, la correlación de una cantidad dinámica dada se desintegra predominantemente en pares de modos hidrodinámicos con variables conservadas. La Teoría de Modo-Acoplamiento es el formalismo que calcula su acoplamiento.

A partir de la discusión sobre, la velocidad de la partícula etiquetada se acopla a un modo bilineal,\(A=\rho_{s}(k) J_{x}^{*}(k)\). luego

\[C(t)=\left\langle v_{x}\left|e^{i \mathcal{L} t}\right| v_{x}\right\rangle \Rightarrow\left\langle v_{x}\left|P e^{i \mathcal{L t}} P\right| v_{x}\right\rangle\]

donde\(P\) está asociado el operador de proyección\(A\). Ampliando el operador de proyección

\[C(t)=\left\langle v_{s} \mid A\right\rangle\langle A \mid A\rangle^{-1}\left\langle A\left|e^{i \mathcal{L} t}\right| A\right\rangle\langle A \mid A\rangle^{-1}\left\langle A \mid v_{s}\right\rangle\]

Ahora, utilice los modos hidrodinámicos lineales para evaluar la función de correlación.

\[\begin{aligned} \rho_{s}=e^{-i k r_{s}} \\ J_{x}=\sum_{i} v_{x i} e^{-i k r_{i}} \end{aligned}\]

Entonces

\[\left\langle v_{s} \mid A\right\rangle=\sum_{i}\left\langle v_{x s} \mid e^{-i k r_{s}} v_{x i} e^{i k r_{i}}\right\rangle=v_{o}^{2}\]

y

\[\langle A \mid A\rangle=N v_{o}^{2}\]

para que

\[\left\langle v_{s} \mid A\right\rangle\langle A \mid A\rangle^{-1}=\frac{1}{N}\]

Por lo tanto,

\[\begin{aligned} C(t)=\frac{1}{N^{2}} \sum_{k} \sum_{k^{\prime}}\left\langle A(k)\left|e^{i \mathcal{L} t}\right| A\left(k^{\prime}\right)\right\rangle \\ \approx \frac{1}{N^{2}} \sum_{k} \sum_{k^{\prime}}\left\langle\rho_{s}(k, t) \mid \rho_{s}\left(k^{\prime}, 0\right)\right\rangle\left\langle J_{x}(k, t) \mid J_{x}\left(k^{\prime}, 0\right)\right\rangle \\ =\frac{1}{N} \sum_{k} F_{s}(k, t) C_{t}(k, t) \\ =\frac{V}{N} \frac{1}{(2 \pi)^{3}} \int d \vec{k} F_{s}(\vec{k}, t) C_{t}(\vec{k}, t) \end{aligned}\]

Ahora,

\[F_{s}(\vec{k}, t)=e^{-k^{2} D t}\]

y

\[C_{t}(\vec{k}, t)=v_{o}^{2} e^{-k^{2} \nu t}\]

Entonces

\[C(t)=\frac{1}{\rho} \frac{v_{o}^{2}}{(2 \pi)^{3}} \int d \vec{k} e^{-k^{2}(D+\nu) t}\]

Al incorporar los tres componentes espaciales de\(J\) y\(v\), tenemos

\[C(t)=\frac{1}{12 \rho} v_{o}^{2}\left[\frac{1}{\pi(D+\nu) t}\right]^{\frac{3}{2}}\]

Referencias

[1] Jean Pierre Hansen e Ian R. McDonald. Teoría de los Líquidos Simples. Burlington, MA: Elsevier Academic Press, 2006.

[2] Donald A. McQuarrie. Mecánica Estadística. Sausalito: Libros de ciencia de la Univerity,\(2000 .\)

[3] Jean-Pierre Boon y Sidney Yip. Hidrodinámica Molecular. Nueva York: McGraw-Hill,\(1980 .\)

[4] Bruce J. Berna y Robert Pecora. Dispersión dinámica de luz: con aplicaciones a química, biología y física. Nueva York: Wiley,\(1976 .\)

[5] Umberto Balucani. Dinámica del Estado Líquido. Nueva York: Prensa de la Universidad de Oxford,\(1994 .\)

[6] B. J. Aliso y T. E. Wainwright. Phys. Rev., A1, 1970. MIT OpenCourseWare

http://ocw.mit.edu

Mecánica Estadística

Primavera 2012

Para obtener información sobre cómo citar estos materiales o nuestros Términos de uso, visite: http://ocw.mit.edu/terms.