4.4: El experimento Joule

Volviendo a la expresión de cambios en la energía interna que se deriva de asumir que\(U\) es una función de\(V\) y\(T\) (o\(U(V, T)\) para abreviar)

\[ dU = \left( \dfrac{\partial U}{\partial V} \right)_TdV+ \left( \dfrac{\partial U}{\partial T} \right)_V dT\]

uno reconoce rápidamente uno de los términos como la capacidad de calor de volumen constante,\(C_V\). Y así la expresión puede ser reescrita

\[ dU = \left( \dfrac{\partial U}{\partial V} \right)_T dV + C_V dT\]

Pero, ¿qué pasa con el primer término? La derivada parcial es un coeficiente llamado “presión interna”, y dado el símbolo\(\pi_T\).

\[ \pi_T = \left( \dfrac{\partial U}{\partial V} \right)_T \]

James Prescott Joule (1818-1889) reconoció que\(\pi_T\) deberían tener unidades de presión (Energía/volumen = presión) y diseñó un experimento para medirlo.

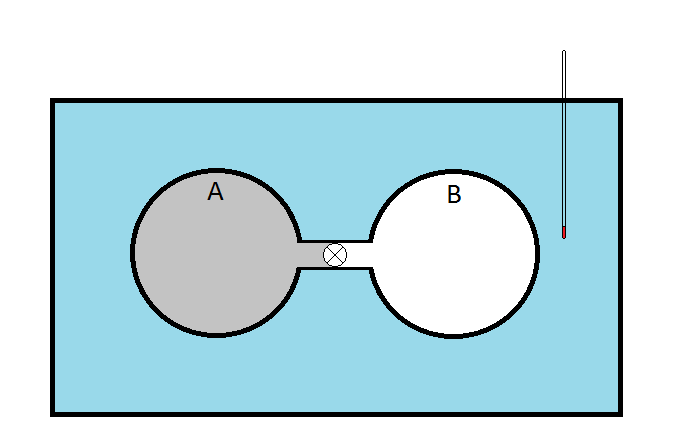
Sumergió dos esferas de cobre, A y B, conectadas por una llave de paso. La esfera A se llena con una muestra de gas mientras que la esfera B fue evacuada. La idea era que cuando se abriera la llave de paso, el gas en la esfera A se expandiría (\(\Delta V > 0\)) contra el vacío en la esfera B (no haciendo ningún trabajo desde entonces\(p_{ext} = 0\). El cambio en la energía interna podría ser expresado

\[ dU = \pi_T dV + C_V dT\]

Pero también, desde la primera ley de la termodinámica

\[ dU = dq + dw\]

Equiparando los dos

\[ \pi_T dV + C_V dT = dq + dw\]

y desde\(dw = 0\)

\[ \pi_T dV + C_V dT = dq \]

Joule concluyó que\(dq = 0\) (y\(dT = 0\) también) ya que no observó un cambio de temperatura en el baño de agua que solo pudo haber sido causado por las esferas metálicas ya sea absorbiendo o emitiendo calor. Y porque\(dV > 0\) para el gas que sufrió la expansión hacia un espacio abierto, ¡también\(\pi_T\) debe ser cero! En verdad, el gas sí sufrió un cambio de temperatura, pero era demasiado pequeño para ser detectado dentro de su precisión experimental. Más tarde, nosotros (una vez que desarrollemos las Relaciones Maxwell) demostraremos que

\[ \left( \dfrac{\partial U}{\partial V} \right)_T = T \left( \dfrac{\partial p}{\partial T} \right)_V -p \label{eq3}\]

Aplicación a un Gas Ideal

Para un gas ideal\(p = RT/V\), por lo que es fácil demostrar que

\[\left( \dfrac{\partial p}{\partial T} \right)_V = \dfrac{R}{V} \label{eq4}\]

así que combinando ecuaciones\ ref {eq3} y\ ref {eq4} juntas para obtener

\[ \left( \dfrac{\partial U}{\partial V} \right)_T = \dfrac{RT}{V} - p \label{eq5}\]

Y como también porque\(p = RT/V\), entonces la Ecuación\ ref {eq5} simplifica a

\[ \left( \dfrac{\partial U}{\partial V} \right)_T = p -p = 0\]

Entonces, si bien la observación de Joule era consistente con limitar el comportamiento ideal, su resultado fue realmente un artefacto de su incertidumbre experimental enmascarando lo que realmente sucedió.

Aplicación a un gas van der Waals

Para un gas van der Waals,

\[ p = \dfrac{RT}{V-b} - \dfrac{a}{V^2} \label{eqV1}\]

por lo

\[\left( \dfrac{\partial p}{\partial T} \right)_V = \dfrac{R}{V-b} \label{eqV2}\]

y

\[ \left( \dfrac{\partial U}{\partial V} \right)_T = T\dfrac{R}{V-b} - p \label{eqV3}\]

Sustitución de la expresión para\(p\) (Ecuación\ ref {EQv1}) en esta Ecuación\ ref {EQv3}

\[ \left( \dfrac{\partial U}{\partial V} \right)_T = \dfrac{a}{V^2}\]

En general, se puede demostrar que

\[\left( \dfrac{\partial p}{\partial T} \right)_V = \dfrac{\alpha}{\kappa_T}\]

Y así la presión interna se puede expresar completamente en términos de propiedades medibles

\[ \left( \dfrac{\partial U}{\partial V} \right)_T = T \dfrac{\alpha}{\kappa_T}-p\]

¡y no es necesario aplicar solo a gases (reales o ideales)!