4.5: El efecto Joule-Thomson
- Page ID
- 72250
En 1852, trabajando con William Thomson (quien más tarde se convertiría en Lord Kelvin), Joule realizó un experimento en el que bombeaban gas a un ritmo constante a través de una tubería de plomo que estaba ceñida para crear una construcción. En el lado aguas arriba de la constricción, el gas estaba a una presión mayor que en el lado aguas abajo de la constricción. Además, se monitoreó cuidadosamente la temperatura del gas a ambos lados de la construcción. El enfriamiento que observaron a medida que el gas se expandió de una región de alta presión a una región de menor presión fue extremadamente importante y condujo a un diseño común de refrigeradores modernos.
No todos los gases experimentan un efecto de enfriamiento al expandirse. Algunos gases, como el hidrógeno y el helio, experimentarán un efecto de calentamiento al expandirse en condiciones cercanas a la temperatura y presión ambiente. La dirección del cambio de temperatura se puede determinar midiendo el coeficiente de Joule-Thomson,\(\mu_{JT}\). Este coeficiente tiene la definición
\[ \mu_{JT} \equiv \left( \dfrac{\partial T}{\partial p} \right)_H\]
Esquemáticamente, el coeficiente de Joule-Thomson se puede medir midiendo la caída de temperatura o el aumento que sufre un gas para una caída de presión dada (Figura\(\PageIndex{1}\)). El aparato está aislado para que no se pueda transferir calor hacia adentro o hacia afuera, haciendo que la expansión sea isentálpica.

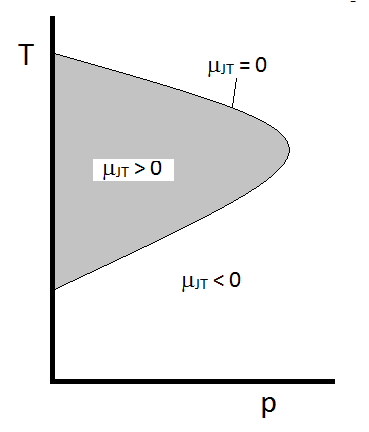
El comportamiento típico del coeficiente de Joule-Thomson se puede resumir en la Figura\(\PageIndex{2}\). En las combinaciones de\(T\) y\(p\) para las cuales\(\mu_{JT} > 0\) (dentro de la región sombreada), la muestra se enfriará al expandirse. En aquellas\(p\) y\(T\) condiciones fuera de la región sombreada, donde\(\mu_{JT} < 0\), el gas sufrirá un aumento de temperatura al expandirse. Y a lo largo del límite, un gas no sufrirá ni un aumento de temperatura ni disminuirá al expandirse. Para una presión dada, normalmente hay dos temperaturas en las que\(\mu_{JT}\) los cambios indican. Estas son las temperaturas de inversión superior e inferior.
Utilizando las herramientas de las matemáticas, es posible expresar el coeficiente de Joule-Thomson en términos de propiedades medibles. Considerar la entalpía en función de la presión y la temperatura:\(H(p, T)\). Esto sugiere que el diferencial total se\(dH\) puede expresar
\[dH= \left( \dfrac{\partial H}{\partial p} \right)_T dp+ \left( \dfrac{\partial H}{\partial T} \right)_p dT \label{totalH}\]
Se mostrará más adelante (nuevamente, una vez que desarrollemos las Relaciones Maxwell) que
\[\left( \dfrac{\partial H}{\partial p} \right)_T dp = -T \left( \dfrac{\partial V}{\partial T} \right)_p + V\]
Una simple sustitución muestra
\[\left( \dfrac{\partial H}{\partial p} \right)_T dp = - TV \alpha + V = V(1-T\alpha)\]
Entonces
\[ dH = V(1-T\alpha) dP + C_p dT\]
Para un gas ideal\(\alpha = 1/T\),
\[ dH = \cancelto{0}{V\left(1-T\dfrac{1}{T}\right) dP} + C_p dT\]
lo que hace que el primer término desaparezca. Entonces, para la expansión constante de la entalpía (\(dH = 0\)), no puede haber cambio en la temperatura (\(dT = 0\)). ¡Esto significará que los gases solo mostrarán valores distintos de cero por\(\mu_{JT}\) solo porque se desvían del comportamiento ideal!
Ejemplo\(\PageIndex{1}\):
Derivar una expresión para\(\mu_{JT}\) en términos de\(\alpha\),\(C_p\),\(V\), y\(T\).
Solución
Usando el diferencial total para\(H(p, T)\) (Ecuación\ ref {totalH}):
\[dH= \left( \dfrac{\partial H}{\partial p} \right)_T dp+ \left( \dfrac{\partial H}{\partial T} \right)_p dT\]
Dividiendo por\(dp\) y limitando a constante\(H\):
\[\left.\dfrac{dH}{dp} \right\rvert_{H}= \left( \dfrac{\partial H}{\partial p} \right)_T \left.\dfrac{dp}{dp} \right\rvert_{H} + \left( \dfrac{\partial H}{\partial T} \right)_p \left.\dfrac{dT}{dp} \right\rvert_{H}\]
Señalando que
\[\left.\dfrac{dH}{dp} \right\rvert_{H} = 0\]
\[\left.\dfrac{dp}{dp} \right\rvert_{H} = 1\]
y
\[\left.\dfrac{dT}{dp} \right\rvert_{H} = \left(\dfrac{\partial T}{\partial p} \right)_{H}\]
por lo
\[ 0 = \left( \dfrac{\partial H}{\partial p} \right)_T + \left( \dfrac{\partial H}{\partial T} \right)_p \left(\dfrac{\partial T}{\partial p} \right)_{H}\]
Entonces podemos usar las siguientes sustituciones:
\[\left( \dfrac{\partial H}{\partial p} \right)_T = V(1-T \alpha)\]
\[\left( \dfrac{\partial H}{\partial T} \right)_p = C_p\]
\[\left(\dfrac{\partial T}{\partial p} \right)_{H} = \mu_{JT}\]
Para obtener
\[ 0 = V(1-T \alpha) + C_p \mu_{JT}\]
Y resolviendo para\(\mu_{JT}\) da
\[\mu_{JT} = \dfrac{V}{C_p}(T \alpha -1)\]


