11.6: Leyes de Tarifas de 2do Orden

Última actualización
Guardar como PDF

Page ID: 72147

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Si la reacción sigue una ley de tasa de segundo orden, se puede emplear alguna metodología. La tarifa se puede escribir como

\[ -\dfrac{d[A]}{dt} = k [A]^2 \label{eq1A}\]

La separación de los términos de concentración y tiempo (esta vez manteniendo el signo negativo a la izquierda por conveniencia) rinde

\[ -\dfrac{d[A]}{[A]^2} = k \,dt \]

La integración se convierte entonces

\[ - \int_{[A]_o}^{[A]} \dfrac{d[A]}{[A]^2} = \int_{t=0}^{t}k \,dt \label{eq1}\]

Y señalando que

\[ - \dfrac{dx}{x^2} = d \left(\dfrac{1}{x} \right)\]

el resultado de la integración Ecuación\ ref {eq1} es

\[ \dfrac{1}{[A]} -\dfrac{1}{[A]_o} = kt\]

\[ \dfrac{1}{[A]} = \dfrac{1}{[A]_o} + kt\]

Y así una trama de\(1/[A]\) como función del tiempo debería producir una gráfica lineal, cuya pendiente es\(k\), y cuya intercepción es\(1/[A]_0\).

Otras leyes ^{de velocidad de segundo} orden son un poco más difíciles de integrar, ya que la integración depende de la estequiometría real de la reacción que se está investigando. Por ejemplo, para una reacción del tipo

\[A + B \rightarrow P\]

Que tiene leyes de tarifas dadas por

\[ -\dfrac{d[A]}{dt} = k [A][B] \]

\[ -\dfrac{d[B]}{dt} = k [A][B] \]

la integración dependerá de la disminución de [A] y [B] (que se relacionará por la estequiometría) que se puede expresar en términos de la concentración del producto [P].

\[[A] = [A]_o – [P] \label{eqr1}\]

\[[B] = [B]_o – [P]\label{eqr2}\]

La concentración depende\(A\) y luego se\(B\) puede eliminar si la ley de tarifas se expresa en términos de la producción del producto.

\[ \dfrac{d[P]}{dt} = k [A][B] \label{rate2} \]

Sustituyendo las relaciones para\([A]\) y\([B]\) (Ecuaciones\ ref {eqr1} y\ ref {eqr2}) en la expresión de ley de tasa (Ecuación\ ref {rate2}) produce

\[ \dfrac{d[P]}{dt} = k ( [A]_o – [P]) ([B] = [B]_o – [P]) \label{rate3} \]

La separación de las variables de concentración y tiempo da como resultado

\[\dfrac{d[P]}{( [A]_o – [P]) ([B] = [B]_o – [P])} = k\,dt\]

Señalando que en su momento\(t = 0\)\([P] = 0\),, la forma integrada de la ley tarifaria se puede generar resolviendo la integral

\[\int_{[A]_o}^{[A]} \dfrac{d[P]}{( [A]_o – [P]) ([B]_o – [P])} = \int_{t=0}^{t} k\,dt\]

Consultar una tabla de integrales revela que para\(a \neq b\) [1],

\[ \int \dfrac{dx}{(a-x)(b-x)} = \dfrac{1}{b-a} \ln \left(\dfrac{b-x}{a-x} \right)\]

La aplicación de la integral definida (siempre y cuando\([A]_0 \neq [B]_0\)) da como resultado

\[ \left. \dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0-[P]}{[A]_0-[P]} \right) \right |_0^{[A]} = \left. k\, t \right|_0^t\]

\[ \dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0-[P]}{[A]_0-[P]} \right) -\dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0}{[A]_0} \right) =k\, t \label{finalint}\]

Sustituir ecuaciones\ ref {eqr1} y\ ref {eqr2} en Ecuación\ ref {finalint} y simplificar (combinar los términos logaritmos naturales) rinde

\[\dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B][A]_o}{[A][B]_o} \right) = kt\]

Para esta ley de tasas, una parcela de\(\ln([B]/[A])\) como función del tiempo producirá una línea recta, cuya pendiente es

\[ m = ([B]_0 – [A]_0)k.\]

En el límite en\([A]_0 = [B]_0\), luego\([A] = [B]\) en todo momento, debido a la estequiometría de la reacción. Como tal, la ley de tarifas se convierte en

\[ \text{rate} = k [A]^2\]

e integrar directo como en la Ecuación\ ref {EQ1a} y la ley de tasa integrada es (como antes)

\[ \dfrac{1}{[A]} = \dfrac{1}{[A]_o} + kt\]

Ejemplo\(\PageIndex{2}\): Confirming Second Order Kinetics

Considere los siguientes datos cinéticos. Utilice una gráfica para demostrar que los datos son consistentes con la cinética de segundo orden. Además, si los datos son de segundo orden, determinar el valor de la constante de velocidad para la reacción.

tiempo (s)	0	10	30	60	100	150	200
[A] (M)	0.238	0.161	0.098	0.062	0.041	0.029	0.023

Solución:

La trama se ve de la siguiente manera:

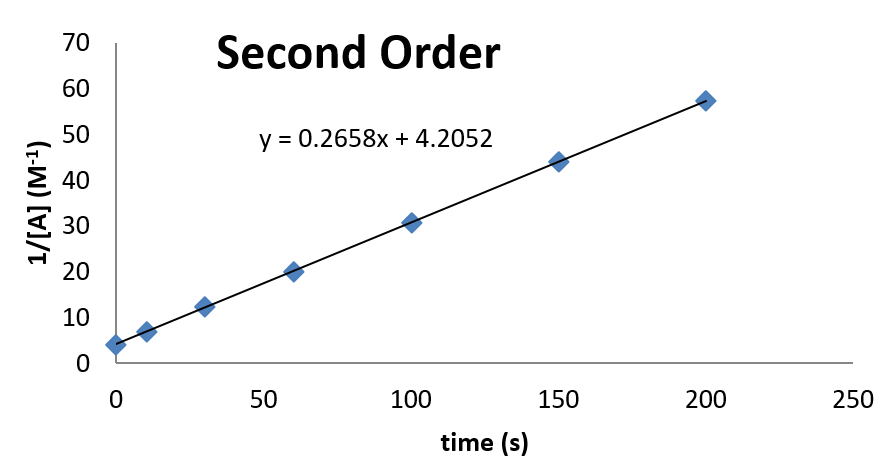
De esta parcela, se puede observar que la constante de velocidad es de 0.2658 M ^-1 s ^-1. La concentración en el momento también se\(t = 0\) puede inferir de la intercepción.

[1] Esta forma integral se puede generar utilizando el método de fracciones parciales. Véase (House, 2007) para una derivación completa.