4.1: La función Onda Especifica el Estado de un Sistema

Objetivos de aprendizaje

• Introducir el primer postulado de la mecánica cuántica
• Reconocer categorías de función de onda no válidas

En la mecánica clásica, la configuración o estado de un sistema viene dada por un punto\(( x , p )\) en el espacio de coordenadas y momenta. Esto especifica todo lo demás en el sistema de una manera totalmente determinista, en que cualquier observable\(Q\) que pueda expresarse como se\(Q ( x , p )\) pueda encontrar, y cualquiera que no pueda es irrelevante. Sin embargo, como hemos visto con la difracción de electrones, es imposible conocer tanto la posición como el momento del electrón exactamente en cada punto a lo largo de la trayectoria. Esto se expresa matemáticamente como el famoso principio de incertidumbre posición-impulso. De ahí que especificar un estado por\(( x , p )\) en la mecánica clásica claramente no funcionará en la mecánica cuántica. Entonces, ¿qué especifica el estado de un sistema cuántico? Aquí es donde entra en juego el primer Postulado de la mecánica cuántica.

Postulado I

El estado del sistema está completamente especificado por\(\psi\). Toda la información posible sobre el sistema se puede encontrar en la función de onda\(\psi\).

Las propiedades de un sistema mecánico cuántico están determinadas por una función de onda\(\psi(r,t)\) que depende de las coordenadas espaciales del sistema y el tiempo,\(r\) y\(t\). Para un sistema de partículas individuales,\(r\) es el conjunto de coordenadas de esa partícula\(r = (x_1, y_1, z_1)\). Para más de una partícula,\(r\) se utiliza para representar el conjunto completo de coordenadas\(r = (x_1, y_1, z_1, x_2, y_2, z_2,\dots x_n, y_n, z_n)\). Dado que el estado de un sistema se define por sus propiedades,\(\psi\) especifica o identifica el estado y a veces se llama la función state en lugar de la función wavefunction.

¿Qué\(\psi\) significa? Esto se responde mejor en términos de la densidad de probabilidad\(P(x)\) que determina la probabilidad (densidad) de que un objeto en el estado\(ψ ( x )\) se encuentre en posición\(x\) (la interpretación Born).

\[ \begin{align} P ( x ) &= ψ^*(x)ψ(x) \\[4pt] &= |ψ(x)| ^2 \label{norm} \end{align} \]

Por lo tanto, para funciones de onda válidas (por ejemplo, de buen comportamiento), la probabilidad normalizada en Ecuación se\(\ref{norm}\) mantiene verdadera, de tal manera que la integral en todo el espacio es igual a 1.

\[\int_{-\infty}^\infty \psi^*(x)\psi(x)\;dx=1 \label{4.1.1} \]

Ecuación\ ref {4.1.1} significa que la posibilidad de encontrar una partícula es 100% en algún lugar dentro de todo el espacio (por ejemplo, en algún lugar entre\(-\infty\) y\(+\infty\)). Se dice que una función de onda es integrable al cuadrado si la Ecuación\ ref {4.1.1} puede ser satisfecha (para que la Interpretación Nacida sea aplicable).

Definición: Funciones integrables al cuadrado

Una función de valor complejo\(f(x)\),, es una función integrable al cuadrado si la integral del cuadrado del valor absoluto es finita.

\[\int_{-\infty}^\infty f^*(x) f(x)\;dx < \infty \nonumber \]

Para que esto sea cierto, las integrales de las porciones positiva y negativa de las partes real e imaginaria de ambas\(f(x)\) deben ser finitas.

Examinemos este conjunto de ejemplos con más detalle en la Figura 4.1.1 . La primera función de onda\(ψ_1\) alcanza un pico bruscamente a un valor particular de\(x\), y la densidad de probabilidad, siendo su cuadrado, también alcanza su punto máximo allí también. Esta es la función de onda para una partícula bien localizada en una posición dada por el centro del pico, ya que la densidad de probabilidad es alta ahí, y el ancho del pico es pequeño, por lo que la incertidumbre en la posición es muy pequeña.

Figura 4.1.1 : Ejemplos de buenas funciones de onda,\(\psi(x)\), (rojo, arriba) y densidades de probabilidad correspondientes,\(P(x)\), (azul, abajo).

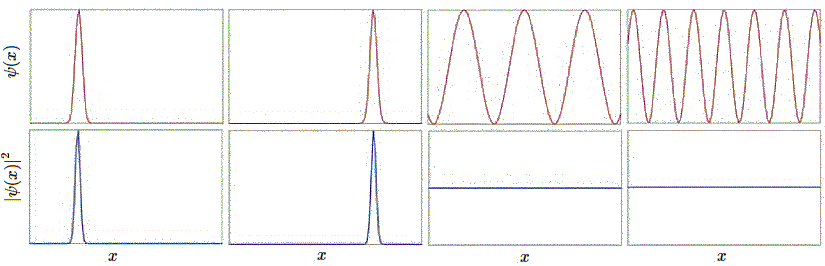
La segunda función de onda\(ψ_2\) tiene el mismo perfil de pico, pero desplazada a un centro de posición diferente. Todas las propiedades de la primera función de onda se mantienen aquí también, así que esto simplemente describe una partícula que está bien localizada en esa posición diferente. Las funciones de onda tercera y cuarta\(ψ_3\) y\(ψ_4\) respectivamente parecen sinusoides de diferentes períodos espaciales. Las funciones de onda son realmente complejas de la forma

\[ψ ( x ) = Ne^{ikx} \nonumber \]

así que solo se está trazando la parte real en la Figura 4.1.1 . Obsérvese que aunque los periodos\(k\),, de las ondulaciones oscilantes son diferentes,

\[ \begin{align*} P(x) &= ψ^*(x)ψ(x) \\[4pt] &= | e^{ikx} |^2 \\[4pt] &= N^2\left(e^{-ikx}\right) \left(e^{ikx}\right) \\[4pt] &= N^2 \end{align*} \nonumber \]

para todos\(k\), por lo que las densidades de probabilidad correspondientes,\(P(x)\), son las mismas a excepción de la constante de normalización (Ecuación\(\ref{norm}\)). Vimos antes que no tiene mucho sentido pensar en una onda sinusoidal como localizada en algún lugar. En efecto, las posiciones para estas dos funciones de onda están mal definidas, por lo que no están bien localizadas, y la incertidumbre en la posición es grande en cada caso. Este es el Principio de Incertidumbre de Heisenberg en acción.

Funciones de onda mal comportadas (inválidas)

La interpretación de Born en Ecuación\(\ref{norm}\) significa que muchas funciones de onda que serían soluciones matemáticas aceptables de la ecuación de Schr ö dinger no son aceptables debido a sus implicaciones para las propiedades físicas del sistema . Para satisfacer esta interpretación, las funciones de onda deben ser:

• valor único,
• continuo, y
• finito.

Estos aspectos significan que la función de onda válida debe ser uno-a-uno, no puede tener una pendiente indefinida, y no puede ir a\(-\infty\) o\(+\infty\). Por ejemplo, la función de onda no debe ser infinita sobre ninguna región finita. Si lo es, entonces la integral en Ecuación\(\ref{4.1.1}\) es igual al infinito. Esto implica que la partícula descrita por tal función de onda tiene una probabilidad cero de estar en cualquier lugar donde la función de onda no sea infinita, pero es seguro que se encuentra en todos los puntos donde la función de onda es infinita.

Figura 4.1.2 : Esta función es una función de onda no válida ya que la amplitud va al infinito sobre una región (el medio en este caso). (CC BY-NC; Ümit Kaya vía LibreTexts)

La interpretación del Born también hace inaceptables soluciones de la ecuación de Schrödinger para la cual\(|ψ(x)|^2\) tiene más de un valor en cualquier momento. Esto sugeriría que había múltiples probabilidades diferentes de encontrar la partícula en ese punto, lo cual es claramente absurdo. El requisito de que el módulo cuadrado de la función de onda debe ser de un solo valor generalmente implica que la función de onda en sí debe ser de valor único. La función en la Figura 4.1.3 viola este requisito. Las líneas grises indican la región donde la función ondulada es multivalor.

Figura 4.1.3 : Esta función es una función de onda no válida ya que no es una función adecuada (es decir, no uno a uno). (CC BY-NC; Ümit Kaya vía LibreTexts)

Surgen otras restricciones porque la función de onda debe satisfacer la ecuación de Schrödinger, que es una ecuación diferencial de segundo orden. Esto implica que debe existir la segunda derivada de la función, lo que implica que existe la primera derivada de la función wavefunction (de lo contrario, la segunda derivada también es indefinida y la función de onda no puede ser una solución de la ecuación de Schrödinger). Las funciones de la Figura 4.1.4 tampoco son aceptables por estas razones.

Figura 4.1.4 : Estas funciones son funciones de onda no válidas. (izquierda) La primera derivada de una función da su gradiente en un punto dado, y así existe siempre y cuando la función sea continua - solo si hay una ruptura en la función hay un punto en el que su primera derivada no existe. (derecha) La segunda derivada de esta función de onda es discontinua en el punto indicado, donde el gradiente de la línea cambia en más de 180º. En la práctica, este requisito puede ser algo flexible, particularmente si la energía potencial del sistema muestra cambios rápidos con la distancia. (CC BY-NC; Ümit Kaya vía LibreTexts)

Ejercicio 4.1.1

Determine si cada una de las siguientes funciones es aceptable como función de onda en las regiones indicadas:

1. \(\cos x \)sobre\((0,\infty)\)
2. \(e^x \)sobre\((-\infty,\infty)\)
3. \(e^{-x} \)sobre\([0,\infty)\)
4. \(\tan \theta\)sobre\([0, 2\theta]\)

Solución a

Esta no es una función de onda aceptable. Es de un solo valor en todo el rango. Hay un solo valor por cada valor de\(x\). Es continuo sobre los límites definidos de integración, como podemos ver en una trama dada a continuación. Sin embargo, no es integrable al cuadrado. \[\int_{0}^{\infty} | \cos(x) |^2 dx \; \xcancel{<} \; \infty \nonumber \]

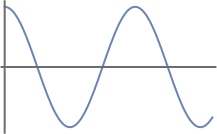
Solución b

Esta no es una función de onda aceptable. Sobre los límites de la integración desde\( -\infty \) hasta\( \infty \), esta función no es integrable al cuadrado. Observe en la gráfica a continuación, cómo la función es indefinida acercándose a los límites de\( \infty \).

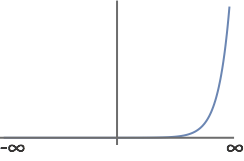
Solución c

Esta es una función de onda aceptable sobre los límites dados. Es finito sobre los límites dados. Es continuo dentro de límites dados. Es de un solo valor. Es integrable al cuadrado con\(\displaystyle \int_{0}^{\infty} | \Psi(x) |^2 dx = \frac{1}{2} \).

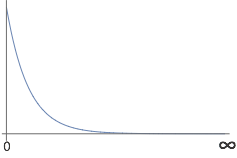
Solución d

Esta no es una función de onda aceptable. Es discontinuo sobre los límites de la integración.

Colaboradores y Atribuciones

• Prof. Allan Adams, Prof. Matthew Evans, Prof. Barton Zwiebach (usado con permiso, MIT OpenCourseWare)