6.7: El átomo de helio no se puede resolver exactamente

Objetivos de aprendizaje

• Agregar electrones al átomo de hidrógeno cuántico da como resultado ecuaciones de Schrödinger analíticamente insol vables (existen, simplemente no tenemos formas analíticas para ellas)
• Un aspecto básico de los correspondientes hamiltonianos multielectrones es que NO son separables con respecto a la coordenada espacial de cada electrón
• Las soluciones a las ecuaciones de Schrödinger de múltiples electrones se denominan funciones de onda multielectrón y a menudo se aproximan como un producto de las funciones de onda de un solo electrón (llamadas aproximación orbital).

Hamiltonianos multi-electrón

El segundo elemento de la tabla periódica proporciona nuestro primer ejemplo de un problema cuántico-mecánico que no se puede resolver exactamente. Sin embargo, como mostraremos, los métodos de aproximación aplicados al helio pueden dar soluciones precisas en perfecta concordancia con los resultados experimentales. En este sentido, se puede concluir que la mecánica cuántica es correcta para átomos más complicados que el hidrógeno. Por el contrario, la teoría de Bohr fracasó miserablemente en los intentos de aplicarla más allá del átomo de hidrógeno.

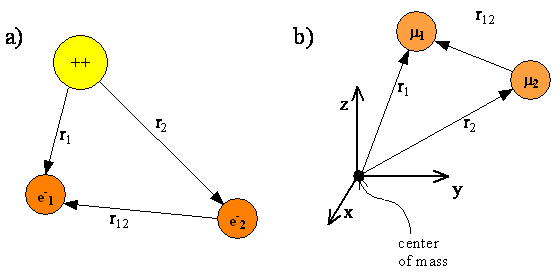
La figura 6.7.1 muestra una representación esquemática de un átomo de helio con dos electrones cuyas coordenadas están dadas por los vectores\(r_1\) y\(r_2\). Los electrones están separados por una distancia\(r_{12} = |r_1-r_2|\). El origen del sistema de coordenadas se fija en el núcleo. Al igual que con el átomo de hidrógeno, los núcleos para los átomos de múltiples electrones son tanto más pesados que un electrón que se supone que el núcleo es el centro de masa. Fijar el origen del sistema de coordenadas en el núcleo nos permite excluir el movimiento traslacional del centro de masa de nuestro tratamiento mecánico cuántico.

Figura 6.7.1 : (a) El núcleo (++) y los electrones (e-) del átomo de helio. b) Partículas reducidas equivalentes con el centro de masa (aproximadamente ubicado en el núcleo) en el origen del sistema de coordenadas. Tenga en cuenta que\(\mu_1\) y\(\mu_2 ≈ m_e\).

El operador hamiltoniano para el átomo de hidrógeno sirve como punto de referencia para escribir el operador hamiltoniano para átomos con más de un electrón. Comience con la misma forma general que usamos para el átomo de hidrógeno Hamiltoniano

\[\hat {H} = \hat {T} + \hat {V} \label {6.7.1} \]

Incluir un término de energía cinética para cada electrón y un término de energía potencial para la atracción de cada electrón cargado negativamente para el núcleo cargado positivamente y un término de energía potencial para la repulsión mutua de cada par de electrones cargados negativamente. El átomo de He Hamiltoniano es

\[ \hat {H} = -\dfrac {\hbar ^2}{2m_e} (\nabla ^2_1 + \nabla ^2_2) + V_1 (r_1) + V_2 (r_2) + V_{12} (r_{12}) \label {6.7.2} \]

donde

\[ V_1(r_1) = -\dfrac {2e^2}{4 \pi \epsilon _0 r_1} \label {6.7.3} \]

\[ V_2(r_2) = -\dfrac {2e^2}{4 \pi \epsilon _0 r_2} \label {6.7.4} \]

\[ V_{12}(r_{12}) = \dfrac {e^2}{4 \pi \epsilon _0 r_{12}} \label {6.7.5} \]

El Hamiltoniano de dos electrones en la Ecuación se\(\ref{6.7.2}\) puede extender a cualquier átomo o ion reemplazando la carga nuclear de He de +2 con una carga general\(Z\); p.

\[V_1(r_1) = -\dfrac {Ze^2}{4 \pi \epsilon _0 r_1} \label {6.7.6} \]

e incluyendo términos para los electrones adicionales. El átomo posterior de múltiples electrones con\(n\) electrón es

\[\hat {H} = \underbrace{-\dfrac {\hbar ^2}{2m_e} \sum_i^n \nabla ^2_i}_{\text{Kinetic Energy}} + \underbrace{\sum_i^n V_i (r_i)}_{\text{Coulombic Attraction}} + \underbrace{ \sum_{i \ne j}^{n,n} V_{ij} (r_{ij})}_{\text{electron-electron Repulsion}} \label {6.7.7} \]

Este hamiltoniano multielectrón es cualitativamente similar al Hamiltoniano de 2 electrones (Ecuación\ ref {6.7.1}) teniendo cada electrón su propia energía cinética y términos de energía potencial nuclear (Ecuaciones\(\ref{6.7.3}\) y\(\ref{6.7.4}\)). La otra gran diferencia entre los sistemas de electrones simples y los sistemas de múltiples electrones es la presencia de los\(V_{ij}(r_{ij})\) términos que contienen\(1/r_{ij}\), donde\(r_{ij}\) está la distancia entre electrones\(i\) y\(j\). Estos términos dan cuenta de la repulsión electrón-electrón que esperamos entre partículas con carga similar.

Ejercicio 6.7.1 : Hamiltonianos de átomos de electrones múltiples

Para el átomo multielectrónico generalizado Hamiltoniano (Ecuación\(\ref{6.7.7}\)):

1. Explicar el origen de cada una de las tres sumatorias.
2. ¿Qué superan estas sumatorias (es decir, cuál es el origen del índice sumador)?
3. Escribir expresiones para\(V_i(r_i)\) y\(V_{ij}(r_{ij})\).

Ejercicio 6.7.2 : Átomo de boro

El boro es el quinto elemento de la tabla periódica (Z=5) y se ubica en el Grupo 13.

1. Escribe el multielectrón Hamiltoniano para un\(\ce{^{11}B}\) átomo.
2. ¿Sería diferente por un\(\ce{^{11}B^{+}}\) ion?
3. ¿Sería diferente para un\(\ce{^{10}B}\) átomo?

Contestar

a.

\[\hat {H}_{\ce{B}}(\vec r_1,\vec r_2,\vec r_3,\vec r_4,\vec r_5) = -\dfrac {\hbar ^2}{2m_e} \sum_i^{5} \nabla ^2_i + \sum_i^{5} \dfrac {-5e^2}{4 \pi \epsilon _0 r_i} + \sum_{i \ne j}^{5,5} \dfrac {e^2}{4 \pi \epsilon _0 r_{ij}} \nonumber \]

que se expande a 20 términos

\[ \begin{align*} \hat {H}_B(\vec r_1,\vec r_2,\vec r_3,\vec r_4,\vec r_5) = &-\dfrac {\hbar ^2}{2m_e} \nabla ^2_1 -\dfrac {\hbar ^2}{2m_e} \nabla ^2_2 -\dfrac {\hbar ^2}{2m_e} \nabla ^2_3 -\dfrac {\hbar ^2}{2m_e} \nabla ^2_4 -\dfrac {\hbar ^2}{2m_e} \nabla ^2_5 \\[4pt] &- \dfrac {-5e^2}{4 \pi \epsilon _0 r_1} - \dfrac {-5e^2}{4 \pi \epsilon _0 r_2} - \dfrac {-5e^2}{4 \pi \epsilon _0 r_3} - \dfrac {-5e^2}{4 \pi \epsilon _0 r_4} - \dfrac {-5e^2}{4 \pi \epsilon _0 r_5} \\[4pt] &+ \dfrac {e^2}{4 \pi \epsilon _0 r_{12}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{13}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{14}} +\dfrac {e^2}{4 \pi \epsilon _0 r_{15}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{23}} +\dfrac {e^2}{4 \pi \epsilon _0 r_{24}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{25}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{34}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{35}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{45}} \end{align*} \nonumber \]

b. si,\(\ce{^{11}B^{+}}\) tiene un electrón menos que\(\ce{^{11}B}\). Su hamiltoniano es

\[\hat {H}_{\ce{B^+}}(\vec r_1,\vec r_2,\vec r_3,\vec r_4 ) = -\dfrac {\hbar ^2}{2m_e} \sum_i^{4} \nabla ^2_i + \sum_i^{4} \dfrac {-5e^2}{4 \pi \epsilon _0 r_i} + \sum_{i \ne j}^{4,4} \dfrac {e^2}{4 \pi \epsilon _0 r_{ij}} \nonumber \]

o ampliado a 14 términos

\[ \begin{align*} \hat {H}_B(\vec r_1,\vec r_2,\vec r_3,\vec r_4) = &-\dfrac {\hbar ^2}{2m_e} \nabla ^2_1 -\dfrac {\hbar ^2}{2m_e} \nabla ^2_2 -\dfrac {\hbar ^2}{2m_e} \nabla ^2_3 -\dfrac {\hbar ^2}{2m_e} \nabla ^2_4 \\[4pt] &- \dfrac {-5e^2}{4 \pi \epsilon _0 r_1} - \dfrac {-5e^2}{4 \pi \epsilon _0 r_2} - \dfrac {-5e^2}{4 \pi \epsilon _0 r_3} - \dfrac {-5e^2}{4 \pi \epsilon _0 r_4} \\[4pt] &+ \dfrac {e^2}{4 \pi \epsilon _0 r_{12}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{13}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{14}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{23}} +\dfrac {e^2}{4 \pi \epsilon _0 r_{24}} + \dfrac {e^2}{4 \pi \epsilon _0 r_{34}} \end{align*} \nonumber \]

c. Sin efecto. Cambiar el número de neutrones en el núcleo no afecta a las energías cinéticas ni potenciales de los electrones. El hamilitoniano para\(\ce{^{10}B}\) es idéntico a\(\ce{^{11}B}\). Esto es técnicamente correcto para este nivel de discusión, pero como veremos más adelante, si ampliamos lo hamiltoniano con estructura hiperfina el número de neutrones puede jugar un papel.

Funciones de onda multielectrón y aproximación orbital

Dado lo que hemos aprendido de los sistemas mecánicos cuánticos anteriores que hemos estudiado, predecimos que las soluciones exactas a la ecuación de Schrödinger multielectrón en Ecuación\(\ref{6.7.7}\) consistirían en una familia de funciones de onda multi-electrón, cada una con un valor propio de energía asociado. Estas funciones de onda y energías describirían los estados terrestres y excitados del átomo de múltiples electrones, así como las ondas de hidrógeno y sus energías asociadas describen los estados terrestres y excitados del átomo de hidrógeno. También predeciríamos que los números cuánticos estarían involucrados.

El hecho de que los electrones interactúen a través de su repulsión de Coulomb significa que una función de onda exacta para un sistema de múltiples electrones sería una sola función que depende simultáneamente de las coordenadas de todos los electrones; es decir, una función de onda multielectrónica,

\[\psi (\vec r _1, \vec r_2, \vec r_3, \vec r_4, \cdots \vec r_n) \nonumber \]

El módulo al cuadrado de tal función de onda describiría la probabilidad de encontrar los electrones (aunque no específicos) en un volumen designado (\(V\)) en el átomo.

\[ p(V)= \int_{V} | \psi (\vec r _1, \vec r_2, \vec r_3, \vec r_4, \cdots \vec r_n) |^2 d\tau \nonumber \]

Todos los electrones se describen simultáneamente mediante una función de onda multielectrónica, por lo que la cantidad total de densidad electrónica representada por la función de onda es igual al número de electrones en el átomo.

\[ \int_{\text{all space}} | \psi (\vec r _1, \vec r_2, \vec r_3, \vec r_4, \cdots \vec r_i) |^2 d\tau = n \nonumber \]

Desafortunadamente, los términos de repulsión de Coulomb (Ecuación\(\ref{6.7.5}\)) hacen imposible encontrar una solución exacta a la ecuación de Schrödinger para muchos átomos de electrones y moléculas incluso para dos átomos de electrones. Tenemos que apoyarnos en aproximaciones y la aproximación orbital es fundamental para los conceptos básicos de química.

La aproximación orbital

Las aproximaciones más básicas a las soluciones exactas a un átomo de múltiples electrones Hamiltoniano,\(\hat{H}\), (Ecuación\ ref {6.7.7}) implican escribir una función de onda multielectrónica (\(\psi (r_1, r_2, \cdots , r_n)\)) como un producto simple de las funciones de onda de un solo electrón (\( \varphi _i (r_i)\)):

\[\psi (r_1, r_2, \cdots , r_n) \approx \varphi _1 (r_1) \varphi _2 (r_2) \cdots \varphi _n(r_n) \label {6.7.8} \]

o en notación Dirac

\[|\psi (r_1, r_2, \cdots , r_n) \rangle \approx | \varphi _1 (r_1) \rangle |\varphi _2 (r_2) \rangle \cdots |\varphi _n(r_n) \rangle\label {6.7.9} \]

La energía del átomo en el estado asociado con una función de onda multielectrónica específica (\(E\)) se obtiene de la ecuación de Schrödinger multielectrón

\[ \hat{H} \psi (r_1, r_2, \cdots , r_n) = E \psi (r_1, r_2, \cdots , r_n) \nonumber \]

Dentro de la aproximación en la Ecuación\ ref {6.7.8}, se\(E\) puede expresar suma de las energías de los componentes de un electrón (\(\epsilon_i\)).

\[ E \approx \sum_i \epsilon_i \nonumber \]

A esto se le llama la aproximación orbital.

Al escribir la función de onda multielectrónica como producto de funciones de un solo electrón (Ecuaciones\ ref {6.7.8} o\ ref {6.7.9}), transformamos conceptualmente un átomo de múltiples electrones en una colección de electrones individuales ubicados en orbitales individuales cuyas características espaciales y energías pueden ser por separado identificado. Para los átomos, estas funciones de onda de un solo electrón se llaman orbitales atómicos y se asemejan a las funciones de onda para átomos similares a hidrógeno. Para las moléculas, como veremos en los siguientes capítulos, estas se denominan orbitales moleculares. Si bien se puede aprender mucho de tal análisis, es importante tener en cuenta que una imagen tan discreta y compartimentada de los electrones es una aproximación, aunque poderosa.

Colaboradores y Atribuciones

• Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski