6.6: Momentum Angular Orbital y las Orbitales P
- Page ID
- 80468
- Relacionar el momento angular orbital clásico de una partícula con el equivalente cuántico
- Caracterizar la mangnitude y orientación del momento angular orbital para un electrón en términos de números cuánticos
Momento angular orbital clásico
La cantidad física conocida como momento angular juega un papel dominante en la comprensión de la estructura electrónica de los átomos. Para obtener una imagen física y una sensación por el momento angular es necesario considerar un sistema modelo desde el punto de vista clásico. El modelo clásico más simple del átomo de hidrógeno es aquel en el que el electrón se mueve en una órbita circular con una velocidad constante o velocidad angular (Figura 6.6.1 ). Así como el momento lineal\(m\vec{v}\) juega un papel dominante en el análisis del movimiento lineal, así el momento angular (\(L\)) juega el papel central en el análisis de un sistema con movimiento circular como se encuentra en el modelo del átomo de hidrógeno.
En la Figura 6.6.1 ,\(m\) se encuentra la masa del electrón,\(\vec{v}\) es la velocidad lineal (la velocidad que poseería el electrón si continuara moviéndose a una tangente a la órbita) y\(r\) es el radio de la órbita. La velocidad lineal\(\vec{v}\) es un vector ya que posee en cualquier instante tanto una magnitud como una dirección en el espacio. Obviamente, a medida que el electrón gira en la órbita la dirección de\(\vec{v}\) cambia constantemente, y así el impulso lineal no\(m\vec{v}\) es constante para el movimiento circular. Esto es así a pesar de que la velocidad del electrón (es decir,\(\vec{v}\) cuya magnitud se denota por\(|\vec{v}|\)) permanece sin cambios. Según la segunda ley de Newton, una fuerza debe estar actuando sobre el electrón si su impulso cambia con el tiempo. Esta es la fuerza que impide que el electrón vuele en tangente a su órbita. En un átomo la fuerza de atracción que contiene el electrón es la fuerza electrostática de atracción entre el núcleo y el electrón, dirigida a lo largo del radio r en ángulo recto con la dirección del movimiento del electrón.
El momento angular, al igual que el momento lineal, es un vector y se define de la siguiente manera:
\[|\vec{L}| = m \nu r \nonumber \]
El momento angular vect o\(\vec{L}\) se dirige a lo largo del eje de rotación. De la definición es evidente que el vector de momento angular permanecerá constante siempre y cuando la velocidad del electrón en la órbita sea constan t (\(|\vec{v}|\)re red sin cambios) y el plano y radio de la órbita permanezcan inalterados. Así, para una órbita dada, el momento angular es constante siempre y cuando la velocidad angular de la partícula en la órbita sea constante. En un átomo la única fuerza sobre el electrón en la órbita se dirige alon g\(r\); no tiene componente en la dirección del movimiento. La fuerza actúa de tal manera que cambia solo el impulso lineal. Por lo tanto, mientras que el impulso de la oreja lin no es constante durante el movimiento circular, el momento angular lo es. Una fuerza ejercida sobre la partícula en la dirección del vector\(\vec{v}\) cambiaría la velocidad angular y el momento angular. Cuando se aplica una fuerza que hace cha nge\(\vec{L}\), se dice que un par actúa sobre el sistema. Así, el momento angular y el par están relacionados de la misma manera que el momento y la fuerza lineales.
Momento angular cuántico
El punto importante de la discusión anterior es que tanto el momento angular como la energía de un átomo permanecen constantes si el átomo se deja intacto. Cualquier cantidad física constante en un sistema clásico se conserva y cuantifica en un sistema mecánico cuántico. Así, tanto la energía como el momento angular se cuantifican para un átomo.
Cualquier cantidad física constante en un sistema clásico se conserva y cuantifica en un sistema mecánico cuántico.
Hay un número cuántico, denotado por\(l\), que gobierna la magnitud del momento angular, así como el número cuántico\(n\) determina la energía. La magnitud del momento angular puede asumir solo aquellos valores dados por:
\[ |L| = \sqrt{l(l+1)} \hbar \label{4} \]
con\(l = 0, 1, 2, 3, ... n-1\).
Además, el valor de n limita el valor máximo del momento angular ya que el valor de l no puede ser mayor que n - 1. Para el estado n = 1 discutido anteriormente,\(l\) puede tener el valor de cero solamente. Cuando n = 2, l puede ser igual a 0 o 1, y para n = 3, l = 0 o 1 o 2, etc. cuando l = 0, es evidente a partir de la Ecuación\(\ref{4}\) que el momento angular del electrón es cero. Los orbitales atómicos que describen estos estados de momento angular cero se denominan orbitales s. Los orbitales s se distinguen entre sí al indicar el valor de n, el número cuántico principal. Se les conoce como los 1 s, 2 s, 3 s, etc., orbitales atómicos.
La discusión anterior se refirió al orbital 1s ya que para el estado fundamental del átomo de hidrógeno\(n = 1\) y\(l = 0\). Este orbital, y todos los orbitales en general, predicen distribuciones de densidad esférica para el electrón como se discutió anteriormente.
Es de uso común referirse a un electrón como estar “en” un orbital aunque lo sea, pero una función matemática sin realidad física. Decir que un electrón está en un orbital particular significa implicar que el electrón está en el estado cuántico que es descrito por ese orbital. Por ejemplo, cuando el electrón está en el orbital de 2 s el átomo de hidrógeno se encuentra en un estado para el cual\(n = 2\) y\(l = 0\).
Al comparar estos resultados con los de la órbita de 1 s en la Figura 6.6.2 vemos que a medida que\(n\) aumenta el valor promedio de\(r\) aumentos. Esto concuerda con el hecho de que la energía del electrón también aumenta a medida que\(n\) aumenta. El aumento de la energía da como resultado que el electrón esté en promedio alejado de la fuerza de atracción del núcleo. Como en el ejemplo simple de un electrón que se mueve sobre una línea, los nodos (valores\(r\) para los cuales la densidad electrónica es cero) aparecen en las distribuciones de probabilidad. El número de nodos aumenta con el aumento de la energía y es igual\(n - 1\).
Cuando el electrón posee momento angular las distribuciones de densidad ya no son esféricas. De hecho, para cada valor de\(l\), la distribución de densidad electrónica asume una forma característica en la Figura 6.6.2 .
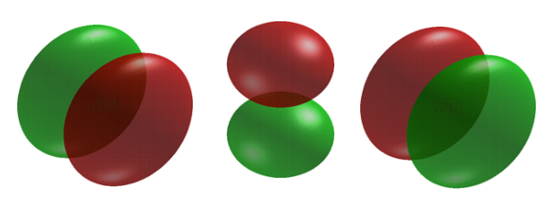
Cuando\(l = 1\), los orbitales se llaman p orbitales. En este caso el orbital y su densidad electrónica se concentran a lo largo de una línea (eje) en el espacio. La función orbital o onda 2 p es positiva en valor en un lado y negativa en valor en el otro lado de un plano que es perpendicular al eje de la órbita y pasa a través del núcleo. El orbital tiene un nodo en este plano, y en consecuencia un electrón en un orbital de 2 p no coloca ninguna densidad de carga electrónica en el núcleo. La densidad electrónica de un orbital de 1 s, por otro lado, es un máximo en el núcleo. Se obtiene el mismo diagrama para la distribución de densidad de 2 p para cualquier plano que contenga este eje. Así, en tres dimensiones la densidad electrónica parecería estar concentrada en dos lóbulos, uno a cada lado del núcleo, siendo cada lóbulo circular en sección transversal Figura 6.6.3 .
Un electrón posee momento angular orbital tiene una distribución de densidad ya no es esférica.
El número\(m_l\) cuántico y los campos magnéticos
El número cuántico magnético, designado por la letra\(m_l\), es el tercer número cuántico que describe el estado cuántico único de un electrón. El número cuántico magnético distingue los orbitales disponibles dentro de una subcapa, y se utiliza para calcular el componente acimutal de la orientación de la órbita en el espacio. Al igual que con nuestra discusión sobre los rotores rígidos, el número cuántico\(m_l\) se refiere a la proyección del momento angular en esta dirección elegida arbitrariamente, convencionalmente llamada\(z\) dirección o eje de cuantificación. \(L_z\), la magnitud del momento angular en la dirección z, viene dada por la fórmula
\[ L_z = m_l \hbar \nonumber \]
El número cuántico\(m_l\) se refiere, de manera holgada, a la dirección del vector de momento angular. El número cuántico magnético\(m_l\) sólo afecta a la energía del electrón si se encuentra en un campo magnético porque en ausencia de uno, todos los armónicos esféricos correspondientes a los diferentes valores arbitrarios de\(m_l\) son equivalentes. El número cuántico magnético determina el desplazamiento de energía de un orbital atómico debido a un campo magnético externo (esto se llama el efecto Zeeman), de ahí el nombre número cuántico magnético. Sin embargo, el momento dipolar magnético real de un electrón en un orbital atómico llega no sólo del momento angular del electrón, sino también del espín electrónico, expresado en el número cuántico de espín, que es el cuarto número cuántico. \(m_s\)y discutido en el siguiente capítulo.
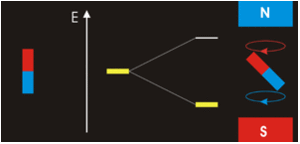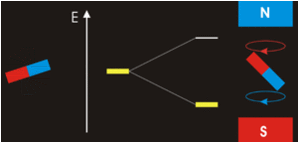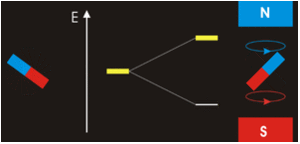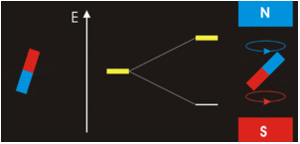
La respuesta es complicada; mientras que\(m_l=0\) corresponde al\(p_z\), los orbitales para\(m_l=+1\) y se\(m_l=−1\) encuentran en el plano xi (ver Armónicos Esféricos), pero no en los ejes. La razón de este resultado es que las funciones de onda suelen formularse en coordenadas esféricas para facilitar las matemáticas, pero las gráficas en las coordenadas cartesianas tienen un sentido más intuitivo para los humanos. Los\(p_y\) orbitales\(p_x\) y los orbitales se construyen a través de un enfoque de combinación lineal a partir de ondas radiales y angulares y se convierten en\(xy\) (esto se discutió anteriormente). Así, no es posible correlacionar directamente los valores de\(m_l=±1\) con orbitales específicos. La noción de que podemos hacerlo a veces se presenta en cursos introductorios para hacer un modelo matemático complejo un poco más simple e intuitivo, pero es incorrecto.
Las tres funciones de onda para\(n=2\) y\(l=1\) son las siguientes.
\[ \begin{align} |\psi_{2,1,0} \rangle &=r \cos θR(r) \\[4pt] |\psi_{2,1,+1} \rangle &=−\dfrac{r}{2} \sinθ e^{iϕ} R(r) \\[4pt] |\psi_{2,1,-1} \rangle &=+\dfrac{r}{2} \sinθ e^{-iϕ} R(r) \end{align} \nonumber \]
La notación es\(|\psi_{n,l,m_l} \rangle\) con\(R(r)\) es el componente radial de esta función de onda,\(θ\) es el ángulo con respecto al eje z y\(ϕ\) es el ángulo con respecto al\(xz\) plano.
\[R(r)=\sqrt{\dfrac{Z^5}{32\pi a_0^5}}\mathrm{e}^{-Zr/2a_0} \nonumber \]
en el que\(Z\) está el número atómico (o probablemente mejor carga nuclear) y\(a_0\) es el radio Bohr.
Al cambiar de coordenadas esféricas a cartesianas, hacemos la sustitución\(z=r \cosθ\), así:
\[|\psi_{2,1,0} \rangle =z R(r) \nonumber \]
Esto es\(\psi_{2p_z}\) ya que el valor de\(\psi \) depende de\(z\): when\(z=0\);\(\psi =0\), que se espera ya que\(z=0\) describe el\(xy\) -plane.
Las otras dos funciones de onda son\(xy\) degeneradas en el plano. Una afirmación equivalente es que estos dos orbitales no se encuentran en los ejes x e y, sino que los bisecan. Por lo tanto, es típico tomar combinaciones lineales de ellas para que la ecuación se vea más bonita. Si algún conjunto de funciones de onda es una solución a la ecuación de Schrödinger, entonces cualquier conjunto de combinaciones lineales de estas funciones de onda también debe ser una solución (Sección 2.4). Podemos hacer esto por la linealidad de la ecuación de Schrödinger.
En las siguientes ecuaciones, vamos a hacer uso de alguna trigonometría, notablemente la fórmula de Euler:
\[ \begin{align} \mathrm{e}^{\mathrm{i}\phi} &=\cos{\phi}+\mathrm{i}\sin{\phi}\\[4pt] \sin{\phi} &= \dfrac{\mathrm{e}^{\mathrm{i}\phi}-\mathrm{e}^{-\mathrm{i}\phi}}{2\mathrm{i}}\\[4pt] \cos{\phi} &= \dfrac{\mathrm{e}^{\mathrm{i}\phi}+\mathrm{e}^{-\mathrm{i}\phi}}{2} \end{align} \nonumber \]
También vamos a usar\(x=\sin θ\cos ϕ\) y\(y=\sin θ \sinϕ \).
\ begin {alinear*}\ psi_ {2p_x} &=\ dfrac {1} {\ sqrt {2}}\ izquierda (\ psi_ {2,1, +1} -\ psi_ {2,1, -1}\ derecha)\\ [4pt] &=\ dfrac {1} {2}\ izquierda (\ mathrm {e} ^ {\ mathrm {i}\ phi} +\ mathrm {e} ^ {-\ mathrm {i}\ phi}\ derecha) r\ sin {\ theta} f (r)\\ [4pt] &=r\ sin {\ theta}\ cos {\ phi} f (r) =xf (r)\\ [4pt]\ psi_ {2p_y} &=\ dfrac {\ mathrm {i} {\ sqrt {2}}\ izquierda (\ psi_ {2,1, +1} +\ psi_ {2,1, -1}\ derecha)\\ [4pt] &=\ dfrac {1} {2\ mathrm {i}}\ izquierda (\ mathrm {e} ^ {\ mathrm {i}\ phi} -\ mathrm {e} ^ {-\ mathrm {i}\ phi}\ derecha) r\ sin {theta} f (r)\\ [4pt] &=r\ sin {\ theta}\ sin {\ phi} f (r) =yf (r)\\\ final {alinear*}
Entonces, mientras\(m_l=0\) corresponde a\(|p_z \rangle\),\(m_l=+1\) y\(m_l=−1\) no puede asignarse directamente a ninguno\(|p_x \rangle\) o\(|p_y \rangle\), sino más bien a una combinación de\(|p_x \rangle\) y\(|p_y \rangle\). Una descripción alternativa es que\(m_l=+1\) podría corresponder\((|p_x \rangle\ + |p_y \rangle )\) y\(m_l=−1\) podría corresponder a\((|p_x \rangle\ - |p_y \rangle)\).
Orbitales D (aún mayores funciones de onda de momento angular)
Cuando\(l = 2\), los orbitales se denominan d orbitales y la Figura 6.6.4 muestra los contornos en un plano para un orbital de 3 d y su distribución de densidad. Observe que la densidad vuelve a ser cero en el núcleo y que ahora hay dos nodos en la órbita y en su distribución de densidad. A medida que aumenta el momento angular del electrón, la distribución de densidad se concentra cada vez más a lo largo de un eje o en un plano en el espacio. Solo los electrones en\(s\) orbitales con momento angular cero dan distribuciones de densidad esféricas y además colocan densidad de carga en la posición del núcleo.
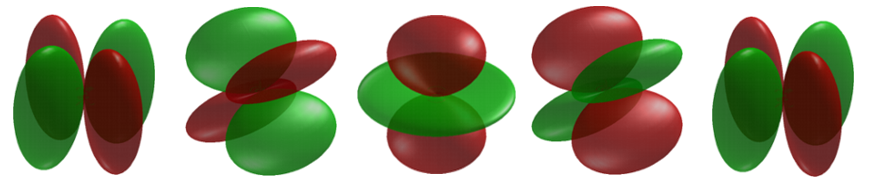
Al igual que con los orbitales p, el único d-orbital al que se\(m_l\) puede atribuir un específico son los\(d_{z^2}\) orbitales con\(m_l=0\). El resto son combinaciones lineales de las funciones de onda del átomo de hidrógeno con componentes angulares armónicos esféricos complejos.
Parece que no hay ni rima ni razón para nombrar los estados correspondientes a los diferentes valores de\(\ell\) (s, p, d, f para l = 0, 1, 2, 3). Este conjunto de etiquetas tuvo su origen en los primeros trabajos de espectroscopia atómica experimental. La letra s representaba aguda, p principal, d difusa y f fundamental en la caracterización de líneas espectrales. A partir de la letra f el nombre de los orbitales es alfabético \(l = 4,5,6 \rightarrow g,h,i, ....\).
Todavía no hemos dado cuenta de la degeneración total de los orbitales de los átomos de hidrógeno que antes dijimos que son\(n^2\) para cada valor de\(n\). Por ejemplo, cuando\(n = 2\), hay cuatro orbitales atómicos distintos. La degeneración restante vuelve a estar determinada por el momento angular del sistema. Dado que el momento angular como el momento lineal es una cantidad vectorial, podemos referirnos a la componente del vector de momento angular que se encuentra a lo largo de algún eje elegido. Por razones que investigaremos, el número de valores que un componente en particular puede asumir para un valor dado de\(l\) is (\(2l + 1\)). Así cuando\(l = 0\), no hay momento angular y no hay más que un solo orbital, un orbital s. Cuando\(l = 1\), hay tres valores posibles para el componente (\(2 \times 1 + 1\)) del momento angular total que son físicamente distinguibles entre sí. Hay, por tanto, orbitales de tres p. De igual manera hay cinco orbitales d, (\(2 \times 2+1\)), siete orbitales f, (\(2 \times 3 +1\)), etc. Todos los orbitales con el mismo valor de\(n\) y\(l\), los tres orbitales 2p por ejemplo, son similares pero difieren en sus orientaciones espaciales.
Para obtener una mejor comprensión de este elemento final de degeneración, debemos considerar con más detalle qué predice la mecánica cuántica respecto al momento angular de un electrón en un átomo.
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski
Dr. Richard F.W. Bader (Professor of Chemistry / McMaster University)
- Stack Exchange (Ben Norris and Loong)

