7.4: La teoría de la perturbación expresa las soluciones en términos de problemas resueltos
- Page ID
- 80364
- Utilizar la teoría de la perturbación para aproximar las energías de los sistemas como una serie de perturbación de un sistema resuelto.
- Utilizar la teoría de la perturbación para aproximar las funciones de onda de los sistemas como una serie de perturbaciones de un sistema resuelto.
Es más fácil calcular los cambios en los niveles de energía y las funciones de onda con un esquema de correcciones sucesivas a los valores de campo cero. Este método, denominado teoría de la perturbación, es el método más importante para resolver problemas en la mecánica cuántica y es ampliamente utilizado en física atómica, materia condensada y física de partículas. La teoría de la perturbación es otro enfoque para encontrar soluciones aproximadas a un problema, partiendo de la solución exacta de un problema relacionado y más simple. Una característica crítica de la técnica es un paso medio que rompe el problema en partes “solucionables” y de “perturbación”. La teoría de la perturbación es aplicable si el problema en cuestión no se puede resolver exactamente, sino que puede formularse agregando un término “pequeño” a la descripción matemática del problema exactamente solucionable.
Comenzamos con un hamiltoniano\(\hat{H}^0\) que ha conocido los propios y las energías propias:
\[ \hat{H}^o | n^o \rangle = E_n^o | n^o \rangle \label{7.4.1} \]
La tarea es encontrar cómo cambian estos autoestados y energías propias si se agrega un término pequeño\(H^1\) (un campo externo, por ejemplo) al hamiltoniano, así:
\[ ( \hat{H}^0 + \hat{H}^1 ) | n \rangle = E_n | n \rangle \label{7.4.2} \]
Es decir, al encender\(\hat{H}^1\) cambia las funciones de onda:
\[ \underbrace{ | n^o \rangle }_{\text{unperturbed}} \Rightarrow \underbrace{|n \rangle }_{\text{Perturbed}}\label{7.4.3} \]
y energías (Figura 7.4.1 ):
\[ \underbrace{ E_n^o }_{\text{unperturbed}} \Rightarrow \underbrace{E_n }_{\text{Perturbed}} \label{7.4.4} \]
La suposición básica en la teoría de la perturbación\(H^1\) es que es lo suficientemente pequeña como para que las correcciones principales sean del mismo orden de magnitud que\(H^1\) ella misma, y las verdaderas energías pueden ser cada vez mejor aproximadas por una serie sucesiva de correcciones, cada una de orden\(H^1/H^o\) comparada con la anterior.
La estrategia es expandir la verdadera función de onda y la correspondiente energía propia como serie en\(\hat{H}^1/\hat{H}^o\). Estas series se alimentan luego en Ecuación\(\ref{7.4.2}\), y los términos del mismo orden de magnitud\(\hat{H}^1/\hat{H}^o\) en los dos lados se establecen iguales. Las ecuaciones así generadas se resuelven una a una para dar resultados progresivamente más precisos.
Para facilitar la identificación de términos del mismo orden en\(\hat{H}^1/\hat{H}^o\) los dos lados de la ecuación, es conveniente introducir un parámetro adimensional\(\lambda\) que siempre va con\(\hat{H}^1\), y luego expandir tanto los estados propios como las energías propias como series de potencia en\(\lambda\),
\[ \begin{align} | n \rangle &= \sum _ i^m \lambda ^i| n^i \rangle \label{7.4.5} \\[4pt] E_n &= \sum_{i=0}^m \lambda ^i E_n^i \label{7.4.6} \end{align} \]
donde\(m\) es cuántos términos en la expansión estamos considerando. El ket\(|n^i \rangle\) se multiplica por\(\lambda^i\) y, por lo tanto, es de orden\((H^1/H^o)^i\).
\(\lambda\)es puramente un dispositivo de contabilidad: ¡lo pondremos igual a 1 cuando hayamos terminado! Simplemente está ahí para hacer un seguimiento de los órdenes de magnitudes de los diversos términos.
Por ejemplo, en la teoría de perturbación de primer orden, las ecuaciones\(\ref{7.4.5}\) se truncan en\(m=1\) (y configuran\(\lambda=1\)):
\[ \begin{align} | n \rangle &\approx | n^o \rangle + | n^1 \rangle \label{7.4.7} \\[4pt] E_n &\approx E_n^o + E_n^1 \label{7.4.8} \end{align} \]
No obstante, consideremos por ahora el caso general. Agregar las expansiones completas para el estado propio (Ecuación\(\ref{7.4.5}\)) y las energías (Ecuación\(\ref{7.4.6}\)) en la ecuación de Schrödinger para la Ecuación de perturbación\(\ref{7.4.2}\) en
\[ ( \hat{H}^o + \lambda \hat{H}^1) | n \rangle = E_n| n \rangle \label{7.4.9} \]
tenemos
\[ (\hat{H}^o + \lambda \hat{H}^1) \left( \sum _ {i=0}^m \lambda ^i| n^i \rangle \right) = \left( \sum_{i=0}^m \lambda^i E_n^i \right) \left( \sum _ {i=0}^m \lambda ^i| n^i \rangle \right) \label{7.4.10} \]
Ya estamos listos para igualar las dos partes término por término en poderes de\(\lambda\). Tenga en cuenta que el término de orden cero, por supuesto, solo devuelve la imperturbable Ecuación de Schrödinger (Ecuación\(\ref{7.4.1}\)).
Veamos la ecuación\(\ref{7.4.10}\) con los primeros términos de la expansión:
\[ \begin{align} (\hat{H}^o + \lambda \hat{H}^1) \left( | n ^o \rangle + \lambda | n^1 \rangle \right) &= \left( E _n^0 + \lambda E_n^1 \right) \left( | n ^o \rangle + \lambda | n^1 \rangle \right) \label{7.4.11} \\[4pt] \hat{H}^o | n ^o \rangle + \lambda \hat{H}^1 | n ^o \rangle + \lambda H^o | n^1 \rangle + \lambda^2 \hat{H}^1| n^1 \rangle &= E _n^0 | n ^o \rangle + \lambda E_n^1 | n ^o \rangle + \lambda E _n^0 | n ^1 \rangle + \lambda^2 E_n^1 | n^1 \rangle \label{7.4.11A} \end{align} \]
Recopilación de términos en orden\(\lambda\) y coloración para indicar diferentes órdenes
\[ \underset{\text{zero order}}{\hat{H}^o | n ^o \rangle} + \color{red} \underset{\text{1st order}}{\lambda ( \hat{H}^1 | n ^o \rangle + \hat{H}^o | n^1 \rangle )} + \color{blue} \underset{\text{2nd order}} {\lambda^2 \hat{H}^1| n^1 \rangle} =\color{black}\underset{\text{zero order}}{E _n^0 | n ^o \rangle} + \color{red} \underset{\text{1st order}}{ \lambda (E_n^1 | n ^o \rangle + E _n^0 | n ^1 \rangle )} +\color{blue}\underset{\text{2nd order}}{\lambda^2 E_n^1 | n^1 \rangle} \label{7.4.12} \]
Si ampliamos Ecuación\(\ref{7.4.10}\) aún más podríamos expresar las energías y las funciones de onda en componentes de orden superior.
Términos de orden cero (\(\lambda=0\))
La recopilación de los términos de orden cero en la expansión (términos negros en la ecuación\(\ref{7.4.10}\)) da como resultado solo la ecuación de Schrödinger para el sistema imperturbable
\[ \hat{H}^o | n^o \rangle = E_n^o | n^o \rangle \label{Zero} \]
Expresión de energía de primer orden (\(\lambda=1\))
Las sumaciones en Ecuaciones\(\ref{7.4.5}\),\(\ref{7.4.6}\), y se\(\ref{7.4.10}\) pueden truncar en cualquier orden de\(\lambda\). Por ejemplo, la teoría de perturbación de primer orden tiene el truncamiento en\(\lambda=1\). Coincidiendo con los términos en los que se linealizan\(\lambda\) (términos rojos en Ecuación\(\ref{7.4.12}\)) y estableciendo\(\lambda=1\) en ambos lados de la\(\ref{7.4.12}\) Ecuación
\[ \hat{H}^o | n^1 \rangle + \hat{H}^1 | n^o \rangle = E_n^o | n^1 \rangle + E_n^1 | n^o \rangle \label{7.4.13} \]
La ecuación\(\ref{7.4.13}\) es la clave para encontrar el cambio de primer orden en la energía\(E_n^1\). Tomando el producto interno de ambos lados con\(\langle n^o | \):
\[ \langle n^o | \hat{H}^o | n^1 \rangle + \langle n^o | \hat{H}^1 | n^o \rangle = \langle n^o | E_n^o| n^1 \rangle + \langle n^o | E_n^1 | n^o \rangle \label{7.4.14} \]
ya que operar el Hamiltoniano de orden cero en la onda del brasierefunción (esto es solo la ecuación de Schrödinger; Ecuación\(\ref{Zero}\)) es
\[ \langle n^o | \hat{H}^o = \langle n^o | E_n^o \label{7.4.15} \]
y a través de la ortonormalidad de las\(| n^o \rangle\) inalteradas funciones de onda
\[ \langle n^o | n^o \rangle = 1 \label{7.4.16} \]
y la ecuación se\(\ref{7.4.8}\) puede simplificar
\[ \bcancel{E_n^o \langle n^o | n^1 \rangle} + \langle n^o | H^1 | n^o \rangle = \bcancel{ E_n^o \langle n^o | n^1 \rangle} + E_n^1 \cancelto{1}{\langle n^o | n^o} \rangle \label{7.4.14new} \]
ya que el conjunto imperturbable de estados propios son ortogonales (Ecuación\ ref {7.4.16}) y podemos cancelar el otro término en cada lado de la ecuación, encontramos que
\[ E_n^1 = \langle n^o | \hat{H}^1 | n^o \rangle \label{7.4.17} \]
El cambio de primer orden en la energía de un estado resultante de agregar un término\(\hat{H}^1\) perturbador al hamiltoniano es solo el valor de expectativa de\(\hat{H}^1\) en las imperturbadas funciones de onda.
Es decir, las energías de primer orden (Ecuación\ ref {7.4.13}) están dadas por
\[ \begin{align} E_n &\approx E_n^o + E_n^1 \\[4pt] &\approx \underbrace{ E_n^o + \langle n^o | H^1 | n^o \rangle}_{\text{First Order Perturbation}} \label{7.4.17.2} \end{align} \]
Estimar la energía del estado fundamental y la primera función de onda de estado excitado dentro de la teoría de perturbación de primer orden de un sistema con la siguiente energía potencial
\ [V (x) =\ comenzar {casos}
V_o & 0\ leq x\ leq L\
\ infty & x< 0\;\ text {and}\; x> L\ final {casos}\ nonumber\]
Solución
El primer paso en cualquier problema de perturbación es escribir el hamiltoniano en términos de un componente imperturbable que se conocen las soluciones (tanto autoestados como energía) y un componente de perturbación (Ecuación\(\ref{7.4.2}\)). Para este sistema, el hamilónico imperturbable y las soluciones es la partícula en una caja infiinitamente alta y la perturbación es un desplazamiento del potencial dentro de la caja por\(V_o\).
\[ \hat{H}^1 = V_o \nonumber \]
Usando la ecuación\(\ref{7.4.17}\) para el término de primer orden en la energía del estado fundamental
\[ E_n^1 = \langle n^o | H^1 | n^o \rangle \nonumber \]
con las funciones de onda conocidas por el problema de la partícula en la caja
\[ | n^o \rangle = \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac {n \pi}{L} x \right) \nonumber \]
En esta etapa podemos hacer dos problemas de forma independiente (es decir, el estado fundamental con\(| 1 \rangle\) y el primer estado excitado\(| 2 \rangle\)). Sin embargo, en este caso, la perturbación de primer orden a cualquier estado de partícula en la caja se puede derivar fácilmente.
\[ E_n^1 = \int_0^L \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac {n \pi}{L} x \right) V_o \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac {n \pi}{L} x \right) dx \nonumber \]
o mejor aún, en lugar de evaluar estas integrales podemos simplificar la expresión
\[ E_n^1 = \langle n^o | H^1 | n^o \rangle = \langle n^o | V_o | n^o \rangle = V_o \langle n^o | n^o \rangle = V_o \nonumber \]
por lo que a través de la ecuación\(\ref{7.4.17.2}\), la energía de cada estado propio perturbado es
\[ \begin{align*} E_n &\approx E_n^o + E_n^1 \\[4pt] &\approx \dfrac{h^2}{8mL^2}n^2 + V_o \end{align*} \nonumber \]
Si bien esta es la perturbación de primer orden a la energía, también es el valor exacto.
Estimar la energía de la función de onda del estado fundamental dentro de la teoría de perturbación de primer orden de un sistema con la siguiente energía potencial
\ [V (x) =\ comenzar {casos}
V_o & 0\ leq x\ leq L/2\
\ infty & x< 0\; and\; x> L\ final {casos}\ nonumber\]
Solución
Al igual que con Example 7.4.1 , reconocemos que componente imperturbable del problema (Ecuación\(\ref{7.4.2}\)) es la partícula en un pozo infinitamente alto. Para este sistema, el hamiltoniano imperturbable y la solución es la partícula en una caja infinitamente alta y la perturbación es un desplazamiento del potencial dentro de media caja por\(V_o\). Esto es esencialmente una función de paso.
Usando Ecuación\(\ref{7.4.17}\) para el término de primer orden en la energía de cualquier estado
\[ \begin{align*} E_n^1 &= \langle n^o | H^1 | n^o \rangle \\[4pt] &= \int_0^{L/2} \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac {n \pi}{L} x \right) V_o \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac {n \pi}{L} x \right) dx + \int_{L/2}^L \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac {n \pi}{L} x \right) 0 \sqrt{\dfrac{2}{L}} \sin \left ( \dfrac {n \pi}{L} x \right) dx \end{align*} \nonumber \]
La segunda integral es cero y la primera integral se simplifica a
\[ E_n^1 = \dfrac{2}{L} \int_0^{L/2} V_o \sin^2 \left( \dfrac {n \pi}{L} x \right) dx \nonumber \]
esto se evalúa para
\[ \begin{align*} E_n^1 &= \dfrac{2V_o}{L} \left[ \dfrac{-1}{2 \dfrac{\pi n}{a}} \cos \left( \dfrac {n \pi}{L} x \right) \sin \left( \dfrac {n \pi}{L} x \right) + \dfrac{x}{2} \right]_0^{L/2} \\[4pt] &= \dfrac{2V_o}{\cancel{L}} \dfrac{\cancel{L}}{4} = \dfrac{V_o}{2} \end{align*} \nonumber \]
La energía de cada estado propio perturbado, vía Ecuación\(\ref{7.4.17.2}\), es
\[ \begin{align*} E_n &\approx E_n^o + \dfrac{V_o}{2} \\[4pt] &\approx \dfrac{h^2}{8mL^2}n^2 + \dfrac{V_o}{2} \end{align*} \nonumber \]
Expresión de primer orden de funciónondulada (\(\lambda=1\))
La expresión general para el cambio de primer orden en la función de onda se encuentra tomando el producto interno de la expansión de primer orden (Ecuación\(\ref{7.4.13}\)) con el sujetador\( \langle m^o |\) con\(m \neq n\),
\[ \langle m^o | H^o | n^1 \rangle + \langle m^o |H^1 | n^o \rangle = \langle m^o | E_n^o | n^1 \rangle + \langle m^o |E_n^1 | n^o \rangle \label{7.4.18} \]
Último término en el lado derecho de la ecuación\(\ref{7.4.18}\)
La última integral en el lado derecho de la Ecuación\(\ref{7.4.18}\) es cero, ya que\(m \neq n\) así
\[ \langle m^o |E_n^1 | n^o \rangle = E_n^1 \langle m^o | n^o \rangle \label{7.4.19} \]
y
\[\langle m^o | n^0 \rangle = 0 \label{7.4.20} \]
Primer término en el lado derecho de la ecuación\(\ref{7.4.18}\)
La primera integral es más complicada y puede expandirse de nuevo en el\(H^o\)
\[ E_m^o \langle m^o | n^1 \rangle = \langle m^o|E_m^o | n^1 \rangle = \langle m^o | H^o | n^1 \rangle \label{7.4.21} \]
desde
\[ \langle m^o | H^o = \langle m^o | E_m^o \label{7.4.22} \]
entonces
\[ \langle m^o | n^1 \rangle = \dfrac{\langle m^o | H^1 | n^o \rangle}{ E_n^o - E_m^o} \label{7.4.23} \]
y por lo tanto la función de onda corregida a primer orden es:
\[ \begin{align} | n \rangle &\approx | n^o \rangle + | n^1 \rangle \\[4pt] &\approx \underbrace{| n^o \rangle + \sum _{m \neq n} \dfrac{|m^o \rangle \langle m^o | H^1| n^o \rangle }{E_n^o - E_m^o}}_{\text{First Order Perturbation Theory}} \label{7.4.24} \end{align} \]
\(\ref{7.4.24}\)La ecuación es esencialmente una expansión de la corrección de función de onda desconocida como una combinación lineal de funciones de onda no perturbadas conocidas\(\ref{7.4.24.2}\):
\[ \begin{align} | n \rangle &\approx | n^o \rangle + | n^1 \rangle \\[4pt] &\approx | n^o \rangle + \sum _{m \neq n} c_{m,n} |m^o \rangle \label{7.4.24.2} \end{align} \]
con los coeficientes de expansión determinados por
\[ c_{m,n} = \dfrac{\langle m^o | H^1| n^o \rangle }{E_n^o - E_m^o} \label{7.4.24.3} \]
Esto se justifica ya que el conjunto de funciones de onda de orden cero originales forma un conjunto de bases completo que puede describir cualquier función.
El cálculo de la perturbación de primer orden a las funciones de onda es en general una suma infinita de elementos de matriz fuera de diagonal de\(H^1\) (Figura 7.4.2 ).
- No obstante, el denominador sostiene que los términos en esta suma serán ponderados por estados que sean de energía comparable. Eso significa que en principio, estas suma se pueden truncar fácilmente basándose en algún criterio.
- Otro punto a considerar es que muchos de estos elementos de la matriz serán iguales a cero dependiendo de la simetría de la\(\{| n^o \rangle \}\) base y\(H^1\) (por ejemplo, algunas\(\langle m^o | H^1| n^o \rangle\) integrales en Ecuación\(\ref{7.4.24}\) podrían ser cero debido a que la integral tiene una simetría impar; ver Ejemplo 7.4.3 ).
Los denominadores en Ecuación\(\ref{7.4.24}\) argumenta que los términos en esta suma serán dictados preferencialmente por estados que sean de energía comparable. Es decir, los autoestados que tienen energías significativamente mayores o menores que el autoestado imperturbable contribuirán débilmente a la función de onda perturbada.
Estimar la energía de la función de onda del estado fundamental asociada con el hamiltoniano usando la teoría de perturbación
\[ \hat{H} = \dfrac{-\hbar}{2m} \dfrac{d^2}{dx^2} + \dfrac{1}{2} kx^2 + \epsilon x^3 \nonumber \]
Solución
El primer paso en un problema de teoría de perturbación es identificar el sistema de referencia con los autoestados y energías conocidos. Para este ejemplo, este es claramente el modelo de oscilador armónico.
Energía
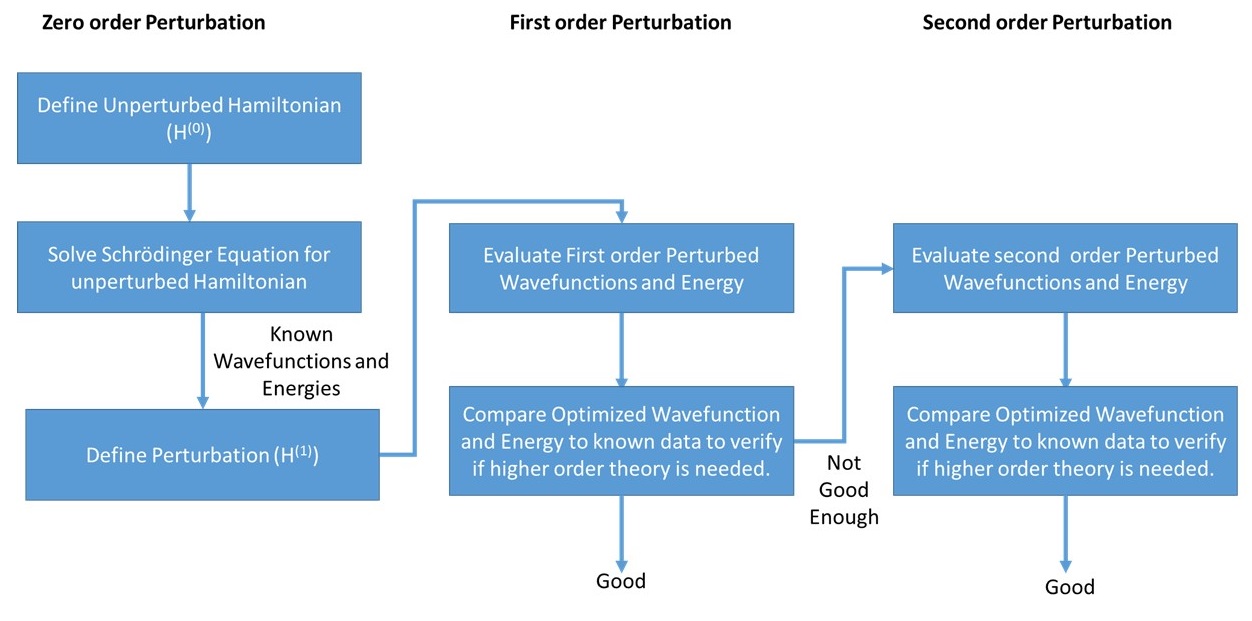
Los primeros pasos en el diagrama de flujo para aplicar la teoría de la perturbación (Figura 7.4.1 ) es separar el hamiltoniano del problema difícil (o insoluble) en uno solucionable con una perturbación. Para este caso, podemos reescribir el hamiltoniano como
\[ \hat{H}^{o} + \hat{H}^{1} \nonumber \]
donde
- \(\hat{H}^{o}\)es el Hamitoniano para el oscilador armónico estándar con estados propios y energías propias conocidas\[ \hat{H}^{(0)}= \dfrac{-\hbar}{2m} \dfrac{d^2}{dx^2} + \dfrac{1}{2} kx^2 \nonumber \]
- \(\hat{H}^{1}\)es la pertubación\[\hat{H}^{1} = \epsilon x^3 \nonumber \]
La perturbación de primer orden viene dada por Ecuación\(\ref{7.4.17}\), que para este problema es
\[E_n^1 = \langle n^o | \epsilon x^3 | n^o \rangle \nonumber \]
Observe que el integrando tiene una simetría impar (i.e.,\(f(x)=-f(-x)\)) siendo impar la perturbación hamiltoniana y siendo pares las funciones de onda del oscilador armónico del estado fundamental. Entonces
\[E_n^1=0 \nonumber \]
Esto significa que para la teoría de pertubación de primer orden, estos términos cúbicos no alteran la energía del estado fundamental (vía Ecuación\(\ref{7.4.17.2})\). Sin embargo, este no es el caso si se utilizó la teoría de perturbación de segundo orden, que es más precisa (no se muestra).
Función Onda
Calcular la perturbación de primer orden a las funciones de onda (Ecuación\(\ref{7.4.24}\)) es más difícil que la energía ya que deben evaluarse múltiples integrales (un número infinito si los argumentos de simetría no son aplicables). Las funciones de onda del oscilador armónico a menudo se escriben en términos de\(Q\), la coordenada de desplazamiento sin escala:
\[ | \Psi _v (x) \rangle = N_v'' H_v (\sqrt{\alpha} Q) e^{-\alpha Q^2/ 2} \nonumber \]
con\(\alpha\)
\[ \alpha =1/\sqrt{\beta} = \sqrt{\dfrac{k \mu}{\hbar ^2}} \nonumber \]
y
\[ N_v'' = \sqrt {\dfrac {1}{2^v v!}} \left(\dfrac{\alpha}{\pi}\right)^{1/4} \nonumber \]
Consideremos solo las primeras seis funciones de onda que utilizan estos polinomios hermitas\(H_v (x)\):
- \(H_0 = 1\)
- \(H_1 = 2x\)
- \(H_2 = -2 + 4x^2\)
- \(H_3 = -12x + 8x^3\)
- \(H_4 = 12 - 48x^2 +16x^4\)
- \(H_5 = 120x - 160x^3 + 32x^5\)
La perturbación de primer orden a la función de onda del estado fundamental (Ecuación\(\ref{7.4.24}\))
\[ | 0^1 \rangle = \sum _{m \neq 0}^5 \dfrac{|m^o \rangle \langle m^o | H^1| 0^o \rangle }{E_0^o - E_m^o} \label{energy1} \]
dadas estas funciones de onda truncadas (técnicamente deberíamos usar la suma infinita) y que estamos considerando solo el estado fundamental con\(n=0\):
\[| 0^1 \rangle = \dfrac{ \langle 1^o | H^1| 0^o \rangle }{E_0^o - E_1^o} |1^o \rangle + \dfrac{ \langle 2^o | H^1| 0^o \rangle }{E_0^o - E_2^o} |2^o \rangle + \dfrac{ \langle 3^o | H^1| 0^o \rangle }{E_0^o - E_3^o} |3^o \rangle + \dfrac{ \langle 4^o | H^1| 0^o \rangle }{E_0^o - E_4^o} |4^o \rangle + \dfrac{ \langle 5^o | H^1| 0^o \rangle }{E_0^o - E_5^o} |5^o \rangle \nonumber \]
Podemos usar la simetría de la perturbación y las funciones de onda imperturbadas para resolver las integrales anteriores. Sabemos que las funciones de onda del oscilador armónico imperturbable\(\{|n^{0}\} \rangle\) alternan entre par (cuando\(v\) es par) e impar (cuando\(v\) es impar) como se muestra anteriormente. Dado que la perturbación es una función impar, solo cuando\(m= 2k+1\) con estas integrales\(k=1,2,3\) serían distintas de cero (es decir, for\(m=1,3,5, ...\)).
Entonces, de las cinco funciones de onda imperturbadas originales, solo\(|m=1\rangle\)\(|m=3\rangle\), y\(|m=5 \rangle\) mezclar para hacer que la función de onda de estado terrestre perturbada de primer orden sea tan
\[| 0^1 \rangle = \dfrac{ \langle 1^o | H^1| 0^o \rangle }{E_0^o - E_1^o} |1^o \rangle + \dfrac{ \langle 3^o | H^1| 0^o \rangle }{E_0^o - E_3^o} |3^o \rangle + \dfrac{ \langle 5^o | H^1| 0^o \rangle }{E_0^o - E_5^o} |5^o \rangle \nonumber \]
En esta etapa, las integrales tienen que ser calculadas manualmente utilizando las funciones de onda definidas anteriormente, las cuales se dejan como un ejercicio. Observe que cada función de onda imperturbada que pueda “mezclarse” para generar la función de onda perturbada tendrá una contribución recíprocamente decreciente (w.r.t. energía) debido al creciente denominador en la Ecuación\ ref {energy1}.
Usar la teoría de la perturbación para estimar la energía de la función de onda del estado fundamental asociada a esta función hamiltoniana
\[ \hat{H} = \dfrac{-\hbar}{2m} \dfrac{d^2}{dx^2} + \dfrac{1}{2} kx^2 + \gamma x^4 \nonumber. \nonumber \]
- Contestar
-
El modelo que estamos usando es el modelo de oscilador armónico que tiene un modelo hamiltoniano
\[H^{0}=-\frac{\hbar}{2 m} \frac{d^2}{dx^2}+\dfrac{1}{2} k x^2 \nonumber \]
Haciendo al perturbado hamiltoniano
\[H^{1}=\gamma x^{4} \nonumber \]
Para encontrar la energía perturbada la aproximamos usando la Ecuación\ ref {7.4.17.2}
\[E^{1}= \langle n^{0}\left|H^{1}\right| n^{0} \rangle \nonumber \]
donde esta la funcion de onda del oscilador armónico de estado fundamental
\[n^{0}=\left(\frac{a}{\pi}\right)^{\left(\frac{1}{4}\right)} e^{-\frac{ax^2}{2}} \nonumber \]
Cuando sustituimos en el hamiltoniano y la ondafunción obtenemos
\[E^{1}=\left\langle\left(\frac{a}{\pi}\right)^{\left(\frac{1}{4}\right)} e^{-\frac{ax^2}{2}}\right|\gamma x^{4}\left|\left(\frac{a}{\pi}\right)^{\left(\frac{1}{4}\right)} e^{-\frac{ax^2}{2}} \right \rangle \nonumber \]
Cambiando esto en forma integral, y combinando las funciones de onda,
\[\begin{align*} E^{1} &=\int_{-\infty}^{\infty}\left(\frac{a}{\pi}\right)^{\left(\frac{1}{2}\right)} e^{\frac{-ax^2}{2}} \gamma x^{4} dx \\[4pt] &=\gamma\left(\frac{a}{\pi}\right)^{\frac{1}{2}} \int_{-\infty}^{\infty} x^{4} e^{-a x^2} d x \end{align*} \nonumber \]
Ahora usamos el valor integral de la tabla
\[\int_{0}^{\infty} x^{2 \pi} e^{-a x^2} dx=\frac{1 \cdot 3 \cdot 5 \ldots (2 n-1)}{2^{m+1} a^{n}}\left(\frac{\pi}{a}\right)^{\frac{1}{2}} \nonumber \]
Dónde enchufamos\(\mathrm{n}=2\) y\(\mathrm{a}=\alpha\) para nuestra integral
\ [\ begin {alineado} E^ {1} &=2\ gamma\ izquierda (\ frac {a} {\ pi}\ derecha) ^ {\ left (\ frac {1} {2}\ derecha)}\ int_ {0} ^ {\ infty} x^ {4} e^ {-a x^2} d x\\
E^ {1} &=2\ gamma\ izquierda (\ frac {a} {\ pi}\ derecha) ^ {\ izquierda (\ frac {1} {2}\ derecha)}\ frac {1\ cdot 3} {2^ {3} a^2}\ izquierda (\ frac {\ pi} {a}\ derecha) ^ {\ frac {1} {2}}\ end {alineado}\ nonumber\]Esta es nuestra energía perturbada
Ahora tenemos que encontrar nuestra energía de estado básico usando la fórmula para la energía de un oscilador armónico que ya conocemos,
\[E_{r}^{0}=\left(v+\dfrac{1}{2}\right) hv \nonumber \]
Donde en el estado fundamental\(v=0\) por lo que la energía para el estado fundamental del oscilador armónico cuántico es
\[E_{\mathrm{r}}^{0}=\frac{1}{2} h v \nonumber \]
Juntar ambos términos energéticos nos da la energía del estado fundamental de la función ondadel hamiltoniano dado,
\ [
\ begin {array} {c}
{E=E^ {0} +E^ {1}}\\
{E=\ frac {1} {2} h v+\ gamma\ frac {3} {4 a^2}}
\ end {array}
\ nonumber\]
Términos de segundo orden (\(\lambda=2\))
Hay términos de energía más altos en la expansión de la Ecuación\(\ref{7.4.5}\) (por ejemplo, los términos azules en Ecuación\(\ref{7.4.12}\)), pero no se discuten más aquí aparte de señalar que todo el proceso de perturbación es una serie infinita de correcciones que idealmente convergen a la respuesta correcta. Está truncando esta serie como un número finito de pasos que es la aproximación. El enfoque general de las aplicaciones de la teoría de perturbaciones está dando en el diagrama de flujo de la Figura 7.4.1 .
Cabe señalar que existen problemas que no pueden resolverse utilizando la teoría de la perturbación, incluso cuando la perturbación es muy débil, aunque tales problemas son la excepción y no la regla. Uno de esos casos es el problema unidimensional de partículas libres perturbadas por un potencial localizado de resistencia\(\lambda\). El encendido de un potencial atractivo arbitrariamente débil hace que la función de onda de partícula\(k=0\) libre caiga por debajo del continuo de las energías de onda plana y se convierta en un estado ligado localizado con energía de enlace de orden\(\lambda^2\). Sin embargo, cambiando el signo de\(\lambda\) para dar un potencial repulsivo no hay estado límite, el estado de onda del plano de energía más baja se mantiene en la energía cero. Por lo tanto, el cambio de energía al encender la perturbación no se puede representar como una serie de potencia en\(\lambda\), la fuerza de la perturbación.
Colaboradores y Atribuciones
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)


http://fizika.unios.hr/~ilukacevic/d...ion_theory.pdf