8.5: Las funciones de onda deben ser antisimétricas para el intercambio de dos electrones cualesquiera
- Page ID
- 79661
- Interpretar la consecuencia del intercambio de dos electrones en un átomo multielectrónico en las longitudes de onda
- Conectar el Principio de Exclusión de Pauli a la simetría de permutación de los átomos de múltiples electrones
La mecánica cuántica nos permite predecir los resultados de los experimentos. Si realizamos un experimento con partículas indistinguibles, una descripción cuántica correcta no puede permitir nada que distinga entre ellas. Por ejemplo, si las ondulaciones de dos partículas se superponen, y detectamos una partícula, ¿cuál es? La respuesta a esto no es sólo que no sabemos, sino que no podemos saber. La mecánica cuántica sólo puede decirnos la probabilidad de encontrar una partícula en una región determinada. Por lo tanto, la función de onda debe describir ambas partículas.
La ecuación de Schrödinger para el átomo de helio es entonces:
\[ \left[ - \dfrac{\hbar^2}{2m} ( \nabla^2_1 + \nabla^2_1 ) - V(\mathbf{r}_1) - V(\mathbf{r}_2) + V_{12}(\mathbf{r}_1,\mathbf{r}_2) \right ] \psi(\mathbf{r}_1, \mathbf{r}_2) = E\psi(\mathbf{r}_1, \mathbf{r}_2) \nonumber \]
donde los subíndices etiquetan cada partícula, y hay seis coordenadas, tres para cada partícula. Si bien\(|\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle \) es una función de onda de seis dimensiones (tres por cada electrón) y contiene toda la información que podemos medir (un Postulado de Mecánica Cuántica), solo proporciona la probabilidad de encontrar el electrón en un elemento de volumen específico, y no nos dice qué partícula es cuál (e.g. ¿es electón\(1\) o electrón\(2\)?).
¿Para qué bases serían apropiados los estados\(|\psi \rangle\)? Si consideramos la aproximación orbital que utiliza una función de onda de producto
\[|\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = |\varphi_a (\mathbf{r}_1) \rangle | \varphi_ b(\mathbf{r}_2)\rangle \nonumber \]
donde\( | \varphi_a(\mathbf{r}_1)\rangle\) y\( | \varphi_b(\mathbf{r}_2)\rangle\) son orbitales de espín de una partícula (con componentes espín y espaciales) de los átomos 1 y 2. Esta aproximación nos permite separar la ecuación de dos partículas en dos ecuaciones de un electrón:
\[ \left[ - \dfrac{\hbar^2}{2m} \nabla^2_1 + V(\mathbf{r}_1) \right ] |\varphi_a(\mathbf{r}_1) \rangle = E|\varphi_a(\mathbf{r}_1) \rangle \nonumber \]
\[ \left[ - \dfrac{\hbar^2}{2m} \nabla^2_2 + V(\mathbf{r}_2) \right ] |\varphi_b(\mathbf{r}_2) \rangle= E|\varphi_a(\mathbf{r}_2) \rangle \nonumber \]
siempre que las partículas no interactúen (por ejemplo,\(\nabla^2_1 \) no actúe sobre\(|\varphi_b(\mathbf{r}_2)\rangle\) y\(V_{12} = 0\)).
Desafortunadamente, al hacer esto hemos introducido etiquetas antifísicas a las partículas indistinguibles. Y esto está mal: el efecto de ello es que las partículas no interfieren entre sí porque están en diferentes dimensiones (espacio de seis dimensiones - ¿recuerdas?). Cuando construimos una función de onda de dos partículas a partir de dos funciones de onda de una partícula, debemos asegurarnos de que la densidad de probabilidad (la cantidad medible\(|\psi|^2\)) sea independiente de las etiquetas artificiales.
El Operador de Intercambio
Podemos profundizar en nuestra comprensión de la descripción mecánica cuántica de los átomos de múltiples electrones examinando en detalle los conceptos de indistinguibilidad electrónica y el Principio de Exclusión de Pauli. Utilizaremos la siguiente declaración como guía para mantener nuestras exploraciones enfocadas en el desarrollo de una imagen clara del átomo de múltiples electrones: “Cuando se construye una función de onda multielectrónica como producto de las funciones de onda de un solo electrón, el concepto correspondiente es que exactamente el valor de carga de un electrón la densidad es descrita por cada espín-orbital atómico”.
Una parte sutil, pero importante del cuadro conceptual, es que los electrones en un sistema multielectrónico no son distinguibles entre sí por ningún medio experimental. Dado que los electrones son indistinguibles, la densidad de probabilidad que calculamos al cuadrar el módulo de nuestra función de onda multielectrónica tampoco puede cambiar cuando los electrones se intercambian (permutan) entre diferentes orbitales. En general, si intercambiamos dos partículas idénticas, el mundo no cambia. Como veremos a continuación, este requisito lleva a la idea de que el mundo se puede dividir en dos tipos de partículas en función de su comportamiento respecto a la permutación o intercambio.
Para que la densidad de probabilidad permanezca sin cambios cuando se permutan dos partículas, la función de onda en sí misma puede cambiar solo por un factor de\(e^{i\varphi}\), lo que representa un número complejo, cuando las partículas descritas por esa función de onda son permutadas. Como mostraremos a continuación, el\(e^{i\varphi}\) factor es posible porque la densidad de probabilidad depende del cuadrado absoluto de la función y todos los valores de expectativa implican\(\psi \psi ^*\). En consecuencia\(e^{i\varphi}\) desaparece en cualquier cálculo que se relacione con el mundo real porque\(e^{i\varphi} e^{-i\varphi} = 1\).
Podríamos escribir simbólicamente una función de onda aproximada de dos partículas como\(\psi (\mathbf{r}_1, \mathbf{r}_2)\). Esto podría ser, por ejemplo, una función de onda de dos electrones para helio. Para intercambiar las dos partículas, simplemente sustituimos las coordenadas de la partícula 1 (\(\mathbf{r}_1\)) por las coordenadas de la partícula 2 (\(\mathbf{r}_2\)) y viceversa, para obtener la nueva función de onda\(\psi (\mathbf{r}_1, \mathbf{r}_2)\). Esta nueva función de onda debe tener la propiedad que
\[|\psi (\mathbf{r}_1, \mathbf{r}_2)|^2 = \psi (\mathbf{r}_2, \mathbf{r}_1)^*\psi (\mathbf{r}_2, \mathbf{r}_1) = \psi (\mathbf{r}_1, \mathbf{r}_2)^* \psi (\mathbf{r}_1, \mathbf{r}_2) \label {8.5.1} \]
ya que la densidad de probabilidad de los electrones en el átomo no cambia tras la permutación de los electrones.
Permutar los electrones la función del producto para He wavefunction:
\[ \psi (\mathbf{r}_1,\mathbf{r}_2) \rangle = | \varphi_{1s}(\mathbf{r}_1) \rangle | \varphi_{1s}(\mathbf{r}_2) \rangle \nonumber \]
La ecuación\(\ref{8.5.1}\) será verdadera solo si las funciones de onda antes y después de la permutación están relacionadas por un factor de\(e^{i\varphi}\),
\[\psi (\mathbf{r}_1, \mathbf{r}_2) = e^{i\varphi} \psi (\mathbf{r}_1, \mathbf{r}_2) \label {8.5.2} \]
para que
\[ \left ( e^{-i\varphi} \psi (\mathbf{r}_1, \mathbf{r}_2) ^*\right ) \left ( e^{i\varphi} \psi (\mathbf{r}_1, \mathbf{r}_2) ^*\right ) = \psi (\mathbf{r}_1 , \mathbf{r}_2 ) ^* \psi (\mathbf{r}_1 , \mathbf{r}_2) \label {8.5.3} \]
Si intercambiamos o permutamos dos partículas idénticas dos veces, estamos (por definición) de vuelta a la situación original. Si cada permutación cambia la función de onda por\(e^{i \varphi}\), la permutación doble debe cambiar la función de onda por\(e^{i\varphi} e^{i\varphi}\). Desde entonces volvemos al estado original, el efecto de la doble permutación debe ser igual a 1; es decir,
\[e^{i\varphi} e^{i\varphi} = e^{i 2\varphi} = 1 \label {8.5.4} \]
que es verdadero solo si\(\varphi = 0 \) o un múltiplo entero de\(\pi\). El requisito de que una doble permutación reproduzca la situación original limita los valores aceptables\(e^{i\varphi}\) para +1 (cuando\(\varphi = 0\)) o -1 (cuándo\(\varphi = \pi\)). Ambas posibilidades se encuentran en la naturaleza.
Usa la igualdad de Euler
\[e^{i\pi} + 1=0 \nonumber \]
para demostrar que\(e^{i 2\varphi} = 1\) cuando\(\varphi = 0\) o\(n \pi\) y en consecuencia\(e^{i \varphi} = \pm 1\).
Podemos introducir el operador de intercambio\(\hat{P}_{12}\): un operador que permuta las etiquetas de las partículas en una función de onda multipartícula. Este es un operador bastante extraño, porque solo cambia las etiquetas antifísicas que hemos adjuntado a las funciones de onda de una partícula para que las matemáticas sean más fáciles. Para una solución significativa debemos tener una función de onda que tenga una amplitud de probabilidad inalterada por\(\hat{P}_{12}\): debe ser simétrica o antisimétrica con respecto al intercambio:
\[\hat{P}_{12} |\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = \pm |\psi(\mathbf{r}_2, \mathbf{r}_1) \rangle \label{exchange} \]
Las soluciones físicas deben ser funciones propias de\(\hat{P}_{12}\) (es decir,\(\hat{H}\) y\(\hat{P_{12}}\) conmutar). Moveover, Equation\ ref {exchange} argumenta que los valores propios del Operador de Intercambio son +1 (bosones) o −1 (fermiones).
Bosones
Las funciones de onda para las cuales se\(e^{i \varphi} = +1\) definen como simétricas con respecto a la permutación, porque la función de onda es idéntica antes y después de una sola permutación. Las funciones de onda que son simétricas con respecto al intercambio de las partículas obedecen a la siguiente relación matemática,
\[\hat{P}_{12} |\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = + |\psi(\mathbf{r}_2, \mathbf{r}_1) \rangle \nonumber \]
El comportamiento de algunas partículas requiere que la función de onda sea simétrica con respecto a la permutación. Estas partículas se llaman bosones y tienen espín entero como núcleos de deuterio, fotones y gluones.
Fermiones
El comportamiento de otras partículas requiere que la función de onda sea antisimétrica con respecto a la permutación\((e^{i\varphi} = -1)\). Una función de onda que es antisimétrica con respecto al intercambio de electrones es aquella cuya salida cambia de signo cuando se intercambian las coordenadas electrónicas, como se muestra a continuación.
\[\hat{P}_{12} |\psi(\mathbf{r}_1, \mathbf{r}_2) \rangle = - |\psi(\mathbf{r}_2, \mathbf{r}_1) \rangle \nonumber \]
Estas partículas se llaman fermiones y tienen espín medio entero e incluyen electrones, protones y neutrinos. Dado que los electrones son fermiones, cualquier función de onda utilizada para describir múltiples electrones debe ser antisimétrica con respecto a la permutación de los electrones. El requisito de que la función de onda sea antisimétrica se aplica a todas las funciones de múltiples electrones\(\psi (\mathbf{r}_1, \mathbf{r}_2, \cdots r_i)\), incluidas las aproximadas como productos de funciones de electrones simples
\[| \psi (\mathbf{r}_1, \mathbf{r}_2, \cdots r_i) \rangle \approx \varphi _a (\mathbf{r}_1) \varphi _b (\mathbf{r}_2) \cdots \varphi _i (r_i) \label{Product} \]
¿Qué se entiende por el término simetría de permutación?
Explicar por qué la función del producto\(\varphi (\mathbf{r}_1) \varphi (\mathbf{r}_2)\) podría describir dos bosones (núcleos de deuterio), pero no puede describir dos fermiones (e.g., electrones).
- Contestar
-
Porque si cambiamos\(\mathbf{r}_1\) y\(\mathbf{r}_2\), la función del producto se convierte\(φ(r_2)φ(r_1)\), que es igual a\(φ(r_1)φ(r_2)\), que es consistente con las funciones de onda de los bosones, porque las funciones de onda de bosón son simétricas. Sin embargo, las funciones de onda de fermión son antisimétricas, lo que significa que si el interruptor r 1 y r 2, el resultado debe ser -1×la función de onda original. Por lo tanto, la función del producto\(φ(r_1)φ(r_2)\) no puede describir fermiones.
El principio de exclusión de Pauli
Cualquier hamiltoniano físicamente significativo debe conmutar con\(\hat{P}_{12}\), de lo contrario\(\hat{H}\) y no\(\hat{P}_{12}\) podría tener funciones propias comunes y el sistema no podría permanecer en un estado propio de intercambio. Una simple función de onda de producto como la de la Ecuación\(\ref{Product}\) no satisface esto (a menos que\( \varphi_a = \varphi_b\)). Se requiere una combinación lineal de todas las permutaciones para satisfacer las restricciones de indistinguibilidad.
Para un sistema de dos partículas (por ejemplo, Helio) existe la combinación asimétrica
\[|\psi^{−} \rangle = \dfrac{1}{\sqrt{2}} |\varphi_a(\mathbf{r}_1)\varphi_b(\mathbf{r}_2) − \varphi_a(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \label{ASym} \]
y combinación simétrica
\[ |\psi^{+} \rangle = C_{ab} |\varphi_a(\mathbf{r}_1)\varphi_b(\mathbf{r}_2) + \varphi_a(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle + C_{aa} |\varphi_a(\mathbf{r}_2)\varphi_a(\mathbf{r}_1) \rangle + C_{bb}|\varphi_b(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \label{Sym} \]
donde los\(C_{ab}\) términos son parámetros de expansión y normalización.
Obsérvese que la combinación antisimétrica (Ecuación\(\ref{ASym}\)) no puede incluir términos donde ambas partículas estén en el mismo estado (espín-orbital), pero existen tres posibilidades para el estado simétrico (Ecuación\(\ref{Sym}\)).
Aunque cualquier combinación lineal de\(C_{ab}\)\(C_{bb}\), y\(C_{aa}\) en Ecuación\(\ref{Sym}\) es posible, hay tres expresiones limitantes para posibles combinaciones simétricas:
\[ \begin{align} |\psi^{+i}_1 \rangle &= C_{ab} |\varphi_a(\mathbf{r}_1)\varphi_b(\mathbf{r}_2) + \varphi_a(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \\[4pt] |\psi^{+i}_2 \rangle &=C_{aa} |\varphi_a(\mathbf{r}_2)\varphi_a(\mathbf{r}_1) \rangle \\[4pt] |\psi^{+i}_3 \rangle &= C_{bb}|\varphi_b(\mathbf{r}_2)\varphi_b(\mathbf{r}_1) \rangle \end{align} \nonumber \]
Si\(\varphi_a(\mathbf{r}_1) = \varphi_a(\mathbf{r}_2)\), entonces\(|\varphi^{−i} \rangle= 0\). Por lo tanto, no existe una combinación antisimétrica posible que involucre electrones en el mismo estado (espín-órbita). Este es el principio de exclusión Pauli.
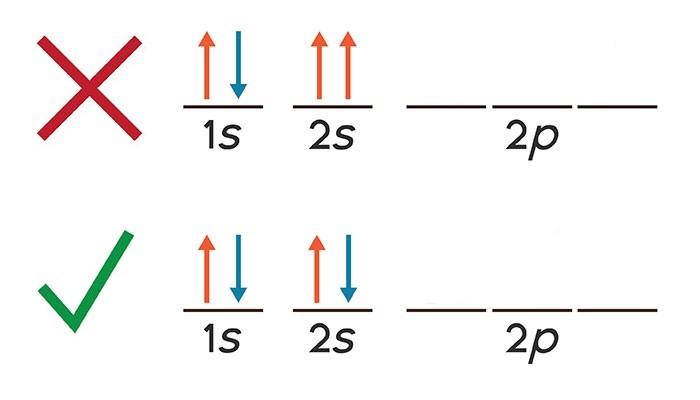
El Principio de Exclusión de Pauli sostiene que dos electrones no podían ser descritos por el mismo spin-orbital. Para ver la relación entre esta afirmación y el requisito de que la función de onda sea antisimétrica para los electrones, intente construir una función de onda antisimétrica para dos electrones que sean descritos por el mismo spin-orbital
\[ |\varphi_b(\mathbf{r}_1) \rangle =\varphi_a(\mathbf{r}_2)\rangle \nonumber \]
Por ejemplo, si este fuera el caso de la combinación antisimétrica para helio (Ecuación\(\ref{ASym}\)), entonces la función de onda colapsa a cero. Solo podemos construir funciones de onda que sean antisimétricas con respecto a la simetría de permutación solo si cada electrón es descrito por una función diferente.
El Principio de Exclusión de Pauli es simplemente el requisito de que la función de onda sea antisimétrica para los electrones, ya que son fermiones.
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski
Graeme Ackland (University of Edinburgh)

