9.4: Estabilidad de enlace químico
- Page ID
- 79877
- Identificar la naturaleza de la energía de los orbitales moleculares de un diatómico en función de la distancia intermolecular
- Identificar las tres integrales involucradas en el cálculo de la Energía Orbital Molecular total: culomb Integral, integral de intercambio e integral de superposición
Como se mostró anteriormente, podemos construir dos orbitales moleculares para el\(\ce{H_2^{+}}\) sistema usando la aproximación LCAO con un conjunto de bases de dos orbitales atómicos 1s (es decir, los\(1s\) orbitales sobre hidrógeno\(A\) (\(1s_A\)) e hidrógeno\(B\) (\(1s_B\)):
\[| \psi _\pm\rangle = \dfrac{1}{\sqrt{2(1 \pm S )}} (1s_A \pm 1s_B) \label{9.3.7a} \]
La energía de estos dos orbitales moleculares puede calcularse a partir del valor de expectativa integral del Hamiltoniano,
\[E_{\pm} = \left \langle \psi _{\pm} | \hat {H} _{elec} | \psi _{\pm} \right \rangle \label {9.4.1} \]
que se puede expandir usando las ondas orbitales moleculares expandidas en Ecuaciones\ ref {9.3.7a} para dar
\[E_{\pm} = \dfrac {1}{2(1 \pm S)} \left[ \underbrace{\left \langle 1s_A |\hat {H} _{elec} | 1s_A \right \rangle}_{H_{AA}} + \underbrace{\left \langle 1s_B |\hat {H} _{elec} | 1s_B \right \rangle }_{H_{BB}}\pm \underbrace{\left \langle 1s_A |\hat {H} _{elec} | 1s_B \right \rangle}_{H_{AB}} \pm \underbrace{\left \langle 1s_B |\hat {H} _{elec} | 1s_A \right \rangle}_{H_{BA}} \right] \label {9.4.2a} \]
donde\(S\) está la integral de superposición entre los dos orbitales atómicos de la base. Las cuatro integrales en Ecuación se\(\ref{9.4.2a}\) pueden representar por\(H_{AA}\)\(H_{BB}\),\(H_{AB}\), y\(H_{BA}\), respectivamente.
\[E_{\pm} = \dfrac {1}{2(1 \pm S)} \left[ H_{AA} + H_{BB} \pm H_{AB} \pm H_{BA} \right] \label {9.4.2b} \]
Mostrar que Ecuación\(\ref{9.4.1}\) se expande para dar Ecuación\(\ref{9.4.2a}\) dentro de la aproximación LCAO que utiliza un conjunto de bases de solo dos orbitales atómicos 1s.
- Contestar
-
Aquí tenemos la función de onda dentro de la aproximación LCAO que utiliza un conjunto de bases de solo dos orbitales atómicos 1s (Ecuación\ ref {9.3.7a}).
\[| \psi_{\pm} \rangle =\frac{1}{\sqrt{2(1 \pm S)}}\left(1_{S a} \pm 1_{S b}\right) \nonumber \]
Y nuestra aproximación LCAO es equivalente a esto si conectamos directamente la función de onda.
\[E_{\pm}= \langle \psi_{\pm}|\hat{H}| \psi_{\pm} \rangle =N^{2} \langle \left(1_{S a} \pm 1_{S b}\right)|\hat{H}|\left(1_{S a}-1_{S b}\right) \rangle \nonumber \]
Podemos ver la forma anterior que la constante de normalización al cuadrado da como resultado:
\[N^{2}=\frac{1}{2(1 \pm S)} \nonumber \]
Ahora ALUMINAMOS el muliple (es decir, término expandido por término):
\[ \langle 1_{S a}|\hat{H}| 1_{S a} \rangle + \langle1_{S b}|\hat{H}| 1_{S b} \rangle \pm \langle 1_{S a}|\hat{H}| 1_{S b} \rangle \pm \langle 1_{S b}|\hat{H}| 1_{S a} \rangle \nonumber \]
Ahora podemos ver que esto es ahora equivalente a la Ecuación\ ref {9.4.2a} si se inserta la ecuación anterior (y agregar un subíndice para enfatizar esto solo se aplica a la función de onda electrónica):
\[E_{\pm} = \dfrac {1}{2(1 \pm S)} \left[ \underbrace{\left \langle 1s_A |\hat {H} _{elec} | 1s_A \right \rangle}_{H_{AA}} + \underbrace{\left \langle 1s_B |\hat {H} _{elec} | 1s_B \right \rangle }_{H_{BB}}\pm \underbrace{\left \langle 1s_A |\hat {H} _{elec} | 1s_B \right \rangle}_{H_{AB}} \pm \underbrace{\left \langle 1s_B |\hat {H} _{elec} | 1s_A \right \rangle}_{H_{BA}} \right] \nonumber \]
Observe que\(A\) y\(B\) aparezcan de manera equivalente en el operador hamiltoniano para\(\ce{H_2^{+}}\). Esta equivalencia significa que las integrales que involucran\(1s_A\) deben ser las mismas que las integrales correspondientes que involucran\(1s_B\), i.e.
\[ H_{AA} = H_{BB} \label {9.4.3} \]
y dado que las funciones de onda son reales
\[ | A \rangle = \langle A | \nonumber \]
por lo
\[H_{AB} = H_{BA} \label {9.4.4} \]
Estas dos igualdades simplifican la Ecuación\ ref {9.4.2b}:
\[ E_{\pm} = \dfrac {1}{1 \pm S} (H_{AA} \pm H_{AB}) \label {9.4.5} \]
Ahora examine los detalles de\(H_{AA}\) después de insertar el operador hamiltoniano para\(\ce{H_2^{+}}\) (Ecuación 9.2.1):
\[H_{AA} = \underbrace{ \left \langle 1s_A \left| - \dfrac {\hbar ^2}{2m} \nabla ^2 - \dfrac {e^2}{4\pi \epsilon _0 r_A} \right| 1s_A \right \rangle }_{\color{red}{E_H}} + \dfrac {e^2}{4\pi \epsilon _0 R} \cancelto{ \color{red} {1}}{ \left \langle 1s_A | 1s_A \right \rangle} \underbrace{ - \left \langle 1s_A \left| \dfrac {e^2}{4 \pi \epsilon _0 r_B } \right| 1s_A \right \rangle}_{ \color{red} {J_{AB}}} \label {9.4.6} \]
- El primer término es solo la integral para la energía del átomo de hidrógeno del orbital 1s,\(E_H\).
- La segunda integral es igual a 1 por normalización; el prefactor es solo la repulsión de Coulomb de los dos protones.
- La última integral, incluyendo el signo menos, está representada por\(J\) y se llama la integral Coulomb.
Físicamente\(J_{AB}\) es la energía potencial de interacción del electrón ubicado alrededor del protón\(A\) con el protón\(B\). Es negativo porque es una interacción atractiva. Es la energía de interacción promedio de un electrón descrita por la\(1s_A\) función con protón\(B\).
El Coulomb Integral es la energía potencial de repulsión electrostática entre el electrón con la densidad electrónica adentro\(1S_A\) y el electrón con la función de densidad electrónica\(1S_B\)
Ahora considere\(H_{AB}\).
\[H_{AB} = \underbrace{ \left \langle 1s_A \left| - \dfrac {\hbar ^2}{2m} \nabla ^2 - \dfrac {e^2}{4\pi \epsilon _0 r_B} \right| 1s_B \right \rangle}_{\color{red}{E_HS}} + \dfrac {e^2}{4\pi \epsilon _0 R} \cancelto{\color{red}{S}}{\left \langle 1s_A | 1s_B \right \rangle} - \underbrace{ \left \langle 1s_A \left| \dfrac {e^2}{4 \pi \epsilon _0 r_A } \right| 1s_B \right \rangle }_ {\color{red} {K_{AB}}}\label {9.4.7S} \]
- En la primera integral tenemos el átomo de hidrógeno Hamiltoniano y la función del átomo de H 1s B. La función 1s B es una función propia del operador con valor propio\(E_H\). Ya que\(E_H\) es una constante factorial fuera de la integral, que luego se convierte en la integral de superposición,\(S\). Por lo tanto, la primera integral se reduce a\(E_HS\).
- El segundo término es solo la energía coulómbica de los dos protones multiplicada por la integral de superposición.
- Al tercer término, incluido el signo menos, se le da el símbolo\(K\) y se denomina la integral de intercambio porque el electrón es descrito por el orbital 1s A en un lado y por el orbital 1s B en el otro lado del operador. El electrón cambia o intercambia posición en la molécula.
En una integral de culombo, el electrón siempre está en el mismo orbital; mientras que, en una Integral de Intercambio, el electrón está en un orbital en un lado del operador y en un orbital diferente en el otro lado.
El uso de las expresiones para\(H_{AA}\) (Ecuación\ ref {9.4.6}) y\(H_{AB}\) (Ecuación\ ref {9.4.7S}) y sustituyendo en Ecuación\(\ref{9.4.5}\) produce:
\[ \begin{align} E_{\pm} &= \dfrac {1}{1 \pm S} \left[ \left(E_H + \dfrac {e^2}{4\pi \epsilon_0 R}\right) (1 \pm S ) + J \pm K \right] \label {9.4.8} \\[4pt] &= E_H + \dfrac {e^2}{4\pi \epsilon _0 R} + \dfrac {J \pm K}{1 \pm S} \label {9.4.9} \end{align} \]
La ecuación nos\(\ref{9.4.9}\) dice que la energía de la\(\ce{H_2^+}\) molécula es la energía de un átomo de hidrógeno más la energía repulsiva de dos protones más algunas interacciones electrostáticas adicionales del electrón con los protones. Estas interacciones adicionales están dadas por el último término
\[ \dfrac {J \pm K}{1 \pm S} \nonumber. \nonumber \]
Si los protones están infinitamente separados entonces solo\(E_H\) es distinto de cero, que podemos establecer a cero restando:
\[ \begin{align} \Delta E_{\pm} &= E_{\pm} - E_H \\[4pt] &= \dfrac {e^2}{4\pi \epsilon _0 R} + \dfrac {J \pm K}{1 \pm S} \label {9.4.10} \end{align} \]
Para obtener un enlace químico y una\(\ce{H_2^+}\) molécula estable\(\Delta E_{\pm}\) debe ser menor a cero y tener un mínimo, es decir,\( \dfrac {J \pm K}{1 \pm S}\) debe ser lo suficientemente negativo para superar la energía repulsiva positiva de los dos protones\(\dfrac {e^2}{4 \pi \epsilon _0R }\) por algún valor de\(R\). Para grande\(R\), estos términos son cero, y para pequeños\(R\), la repulsión de Coulomb de los protones se eleva hasta el infinito.
Mostrar que la Ecuación 9.2.1 sigue de la Ecuación\(\ref{9.4.5}\)
Las integrales de Coulomb y Exchange
Examinaremos más de cerca cómo el término de repulsión de Coulomb y las integrales\(J\)\(K\), y\(S\) dependemos de la separación de los protones, pero primero queremos discutir el significado físico de\(J\), la integral de Coulomb y\(K\), la integral de intercambio. \(J\)y se\(K\) han definido como
\[ J_{AB} = \left \langle 1s_A \left| \dfrac {-e^2}{4 \pi \epsilon _0 r_B } \right|1s_A \right \rangle = - \int \varphi ^*_{1s_A} (r) \varphi _{1s_A} (r) \dfrac {e^2}{4 \pi \epsilon _0 r_B } d\tau \label {9.4.11} \]
\[ K_{AB} = \left \langle 1s_A \left| \dfrac {-e^2}{4 \pi \epsilon _0 r_A } \right|1s_B \right \rangle = - \int \varphi ^*_{1s_A} (r) \varphi _{1s_B} (r) \dfrac {e^2}{4 \pi \epsilon _0 r_A } d\tau \label {9.4.12} \]
La figura 9.4.2 muestra gráficas de los cuatro términos que contribuyen a la energía de\(\ce{H_2^{+}}\) (Ecuación\(\ref{9.4.10}\)). En la Figura 9.4.2 , se puede ver que a medida que la distancia internuclear\(R\) se acerca a cero,
- la repulsión de Coulomb de los dos protones va de cerca de cero a un gran número positivo,
- la integral de superposición va de cero a uno, y
- \(J\)y\(K\) se vuelven cada vez más negativos.

Tenga en cuenta que\(J\) tanto las\(K\) integrales como las integrales son negativas ya que todas las cantidades en los integrandos de la Ecuación\ ref {9.4.11} y\ ref {9.4.12} son positivas. En la integral Coulomb,\(e \varphi ^*_{1s_A} (r) \varphi _{1a_A} (r)\) se encuentra la densidad de carga del electrón alrededor del protón A, ya que r representa las coordenadas del electrón con respecto al protón A. Dado que r B es la distancia de este electrón al protón B, la integral Coulomb da la energía potencial de la carga densidad alrededor del protón A que interactúa con el protón B.\(J\) puede interpretarse como una energía potencial promedio de esta interacción porque\(e \varphi ^*_{1s_A} (r) \varphi _{1a_A} (r)\) es la densidad de probabilidad para el electrón en el punto\(r\), y\(\dfrac {e^2}{4 \pi \epsilon _0 r_B }\) es la energía potencial del electrón en ese punto debido a la interacción con protón B. Esencialmente, J explica la atracción del protón B a la densidad electrónica del átomo de hidrógeno A. A medida que los dos protones se separan más, esta integral va a cero porque todos los valores para r B se vuelven muy grandes y todos los valores para 1/r B se vuelven muy pequeños.
En la integral de intercambio,\(K\), el producto de las dos funciones es distinto de cero solo en las regiones del espacio donde las dos funciones se superponen. Si una función es cero o muy pequeña en algún momento entonces el producto será cero o pequeño. La integral de intercambio también se acerca a cero a medida que aumentan las distancias internucleares porque tanto la superposición como los\(1/r\) valores se vuelven cero. El producto\(e \varphi ^*_{1s_A} (r) \varphi _{1a_B} (r)\) se llama densidad de carga de solapamiento. Dado que la densidad de carga de superposición es significativa en la región del espacio entre los dos núcleos, hace una contribución importante al enlace químico. La integral de intercambio,\(K\), es la energía potencial debido a la interacción de la densidad de carga de superposición con uno de los protones. Si bien\(J\) explica la atracción del protón\(B\) a la densidad electrónica del átomo de hidrógeno\(A\),\(K\) explica la atracción añadida del protón debido a la acumulación de densidad de carga electrónica entre los dos protones.
Escribe un párrafo describiendo en tus propias palabras el significado físico del Coulomb e intercambia integrales por\(\ce{H_2^{+}}\).
La Figura 9.4.3 muestra la energía de H 2 + relativa a la energía de un átomo de hidrógeno separado y un protón como lo da la Ecuación\(\ref{9.4.9}\). Para el electrón en el\(\psi_-\) orbital, la energía de la molécula\(E_{el}(R)\),, siempre es mayor que la energía del átomo y protón separados.
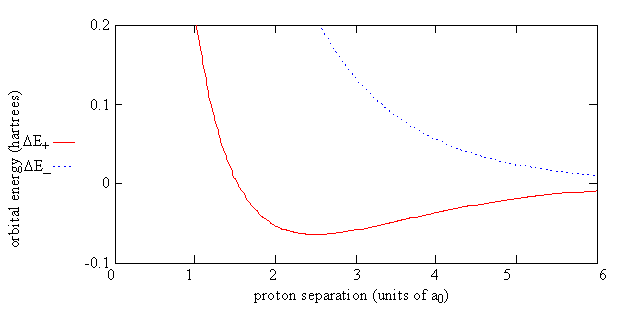
Para el electrón en el\(\psi _+\) orbital, se puede ver que el gran efecto para la energía del orbital de unión,\(E_+(R)\), es el equilibrio entre la repulsión de los dos protones\(\dfrac {e^2}{4 \pi \epsilon _0R }\) y J y K, que son ambos negativos. J y K logran compensar la repulsión de los dos protones hasta que su separación sea menor a las 100pm (es decir, la energía es negativa hasta este punto), y se produce un mínimo en la energía a las 134pm. Este mínimo representa la formación de un enlace químico. El efecto de S es pequeño. Solo hace que el denominador en la Ecuación\(\ref{9.4.9}\) aumente de 1 a 2 a medida que R se acerca a 0.
Para el orbital antiadhesión,\(-K\) es una cantidad positiva y esencialmente cancela J por lo que no hay compensación suficiente para la repulsión de Coulomb de los protones. El efecto de la -K en la expresión, Ecuación\(\ref{9.4.9}\), para\(E_-\) es dar cuenta de la ausencia de densidad de carga de superposición y la repulsión potenciada porque la densidad de carga entre los protones para\(\psi _-\) es incluso menor que la dada por los orbitales atómicos.
Colaboradores y Atribuciones
Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski

