9.3: La Integral de Superposición

Para\(\ce{H2^{+}}\), la molécula más simple, debemos determinar los valores para los coeficientes,\(C_A\) y\(C_B\) para la aproximación LCAO para el orbital molecular como una combinación lineal de los dos orbitales atómicos

\[ |\psi (r) \rangle = C_A 1s_A (r) + C_B1s_B (r) \nonumber \]

Podríamos usar el método variacional lineal para encontrar un valor para estos coeficientes, pero para el caso de\(\ce{H2^{+}}\) evaluar estos coeficientes es fácil. Dado que los dos protones son idénticos, la probabilidad de que el electrón esté cerca\(A\) debe ser igual a la probabilidad de que el electrón esté cerca\(B\). Estas probabilidades están dadas por\(|C_A|^2\) y\(|C_B|^2\), respectivamente. Considerar dos posibilidades que satisfagan la condición

\[|C_A|^2 = |C_B|^2 \nonumber \]

así\(C_A = C_B = C_{+}\) y\(C_A = -C_B = C_{-}\). Estos dos casos producen dos orbitales moleculares:

\[\underbrace{| \psi _+ \rangle = C_+(1s_A + 1s_B)}_{\text{bonding molecular orbital}} \label{9.3.1a} \]

y

\[\underbrace{| \psi _{-} \rangle = C_{-}(1s_A - 1s_B)}_{\text{antibonding molecular orbital}} \label{9.3.1b} \]

La densidad de probabilidad para encontrar el electrón en cualquier punto del espacio viene dada por\(|{\psi}^2|\) y la densidad de carga electrónica es justa\(|e{\psi}^2|\). La diferencia importante entre\(\psi _+\) y\(\psi _{-}\) es que la densidad de carga para\(| \psi_+ \rangle\) se mejora entre los dos protones, mientras que se disminuye para\(|\psi _{-} \rangle\) como se muestra en las Figuras 9.3.1 . \(\psi _{-}\)tiene un nodo en el medio mientras que\(| \psi_+ \rangle\) corresponde a nuestro sentido intuitivo de cómo debe ser un enlace químico. La densidad de carga electrónica se mejora en la región entre los dos protones. Así\(|\psi_+ \rangle\) se llama un orbital molecular de unión. Si el electrón fuera descrito por\(|\psi _{-} \rangle\), la baja densidad de carga entre los dos protones no equilibraría la repulsión Coulomb de los protones, por lo que\(|\psi _{-} \rangle\) se denomina orbital molecular antienlace.

Ahora queremos evaluar\(C_+\)\(C_-\) y luego calcular la energía. El carácter de unión y antiadhesión de\(\psi _+\) y\(\psi _{-}\) también debe reflejarse en la energía. Si\( |\psi _+ \rangle\) efectivamente describe un orbital de enlace, entonces la energía de este estado debería ser menor que la de un protón y un átomo de hidrógeno que están separados. El cálculo de la energía nos dirá si esta teoría simple predice que H ₂ ⁺ sea estable o no y también cuánta energía se requiere para disociar esta molécula.

Las constantes\(C_+\) y\(C_-\) se evalúan a partir de la condición estándar de normalización:

\[ \begin{align} \int \psi ^*_{\pm} \psi _{\pm} d\tau = \left \langle \psi _{\pm} | \psi _{\pm} \right \rangle &= 1 \label {9.3.1} \\[4pt] \left \langle C_{\pm} ( 1s_A \pm 1s_B ) | C_{\pm} ( 1s_A \pm 1s_B ) \right \rangle &= 1 \label {9.3.2} \\[4pt] |C_\pm|^2 [ \underbrace{\langle1s_A | 1s_A \rangle }_{1} + \underbrace{\langle 1s_B | 1s_B \rangle}_{1} \pm \underbrace{ \langle1s_B | 1s_A\rangle}_{S} \pm \underbrace{ \langle1s_A | 1s_B \rangle}_{S^*}] &= 1 \label {9.3.3} \end{align} \]

Dado que los orbitales atómicos están normalizados, las dos primeras integrales son apenas 1. Las dos últimas integrales se denominan integrales superpuestos y están simbolizadas por\(S\) y\(S^*\), respectivamente, ya que una es el conjugado complejo de la otra.

Las integrales superpuestos nos están diciendo que tomemos el valor de 1s _B en un punto multiplicar por el valor de 1s _A en ese punto y sumar (integrar) dicho producto sobre todo el espacio (Figura 9.3.1 ). Si las funciones no se superponen, es decir, si una es cero cuando la otra no lo es y viceversa, estas integrales entonces serán cero. También es posible en general que tales integrales sean cero incluso si las funciones se superponen debido a la cancelación de contribuciones positivas y negativas.

Figura 9.3.1 : Las funciones de onda de los orbitales atómicos disminuyen exponencialmente con la distancia. El solapamiento orbital es distinto de cero cuando dos átomos están muy juntos, como se ilustra para los orbitales de 1s en la figura superior. La cifra inferior muestra orbitales que están demasiado lejos para interactuar. En este caso ambos\(S\) están cerca de cero.

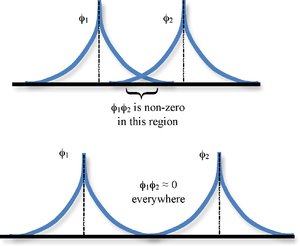
Si la integral de superposición es cero, por cualquier razón, se dice que las funciones son ortogonales. Observe que la integral de superposición varía de 0 a 1 ya que la separación entre los protones varía de\(R = ∞\) a\(R = 0\). Claramente cuando los protones están separados a una distancia infinita, no hay solapamiento, y cuando\(R = 0\) ambas funciones están centradas en un núcleo y\(\left \langle 1s_A | 1s_B \right \rangle\) se vuelven idénticas a\(\left \langle 1s_B | 1s_A \right \rangle\), que se normaliza a 1, porque\(1s_A = 1s_B\).

Con estas consideraciones y utilizando el hecho de que las\(1s\) funciones de onda son reales así

\[ \left \langle 1s_A | 1s_B \right \rangle = \left \langle 1s_B | 1s_A \right \rangle = S \label {9.3.4} \]

La ecuación\(\ref{9.3.3}\) se convierte

\[|C_{\pm}|^2 (2 \pm 2S ) = 1 \label {9.3.5} \]

La solución a la Ecuación\(\ref{9.3.5}\) viene dada por

\[ C_{\pm} = \dfrac{1}{\sqrt{2(1 \pm S )}} \label {9.3.6} \]

Por lo tanto, los orbitales moleculares normalizados en Ecuaciones\(\ref{9.3.1a}\) y\(\ref{9.3.1a}\) son

\[| \psi _+\rangle = \dfrac{1}{\sqrt{2(1 + S )}} (1s_A + 1s_B) \label{9.3.7a} \]

y

\[|\psi _{-} \rangle = \dfrac{1}{\sqrt{2(1 - S )}} (1s_A - 1s_B) \label{9.3.7b} \]

Sin embargo, las energías asociadas con estas funciones de onda requieren un poco más de esfuerzo para calcular como se demuestra en la siguiente sección.

Para la integral de superposición de dos orbitales 1s del dímero de hidrógeno discutido anteriormente es difícil de evaluar analíticamente y se explica aquí. La respuesta final es:

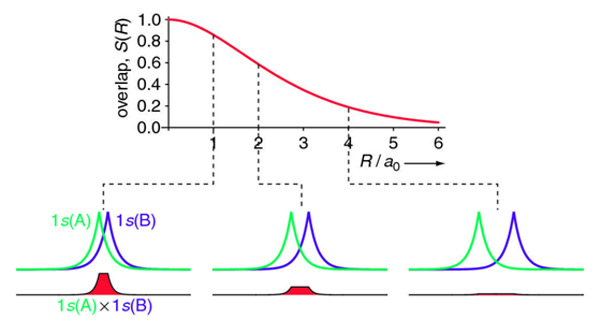
\[ \begin{align} S(R) &= \left \langle 1s_A | 1s_B \right \rangle \\[4pt] &= e^{-R/a_o} \left( 1 +\dfrac{R}{a_o} + \dfrac{R^2}{3a_o^2} \right) \label{overlap} \end{align} \]

La integral de superposición para dos orbitales atómicos 1s de hidrógeno se muestra gráficamente a continuación

Figura 9.3.2 : La integral de superposición en diferentes separaciones de protones.

Ejemplo 9.3.1

Calcular la diferencia en la densidad de carga electrónica (C/pm ³) en un punto a medio camino entre los dos núcleos para\(\ce{H2^{+}}\) para un electrón en el orbital molecular de enlace en comparación con uno en el orbital molecular antienlace.

Solución

La densidad de carga electrónica se calcula con la fórmula\(|e{\psi}^2|\) donde\(e = 1.602 \times 10^{-19} C\)

a: Orbital Molecular de Unión

Primero, la cuadratura del orbital molecular de unión (Ecuación\ ref {9.3.7a}) nos da:

\[ \begin{align*} \psi_+^2 &=\dfrac{1}{2(1 + S )} (1s_A+1s_B)^2 \\[4pt] &= \dfrac{1}{2(1 + S )} \dfrac{1}{\pi a_0^3}\Big(e^{-r_A/a_0}+e^{-r_B/a_0}\Big)^2 \\[4pt] &= \dfrac{1}{2(1 + S )} \dfrac{1}{\pi a_0^3} \\[4pt] &= (0.561)^2\times\left(\dfrac{1}{\pi\times(52.9\;\text{pm})^3}\right)=6.7672\times10^{-7}\;\text{pm}^{-3} \end{align*} \nonumber \]

(Nota: El valor de\(C^2\) se obtiene de la ecuación 9.3.12 y el valor de S es de la Ecuación\ ref {superposición})

Para encontrar la densidad a medio camino entre A y B para el evalulado orbital de unión a 1/2 R,

\(r_A=\dfrac{1}{2}R\)y\(r_B=\dfrac{1}{2}R\)

\[\psi_+^2=3.7\times10^{-7}\;\text{pm}^{-3} \nonumber \]

Ahora multiplica esta respuesta por e para generar la densidad de carga electrónica,

\[P = \Big(3.7\times10^{-7}\;\text{pm}^{-3}\Big)\times\Big(1.602\times10^{-19}\Big)\;\text{C} = 5.93\times10^{-26} C/pm^{3} \nonumber \]

b: Orbital Molecular Antiadhesión

Para encontrar el medio camino entre A y B para el orbital antiunión en\(r_A=\dfrac{1}{2}R\) y\(r_B=\dfrac{1}{2}R\). Sin embargo, la simple inspección de la Ecuación\ ref {9.3.7b} o la Figura 9.3.1 muestra que esto será cero.

\[\text{e}\psi_-^2=0 \nonumber \]

Obviamente, cuando se multiplica por e, la respuesta sigue siendo cero. Esto tiene sentido lógico ya que no habría densidad de carga entre los dos átomos ya que hay un nodo sin probabilidad de encontrar un electrón.

Ejercicio 9.3.1

Mostrar que para dos funciones arbitrarias\(\left \langle \varphi _B | \varphi _A \right \rangle \) es el complejo conjugado de\(\left \langle \varphi _A | \varphi _B \right \rangle \) y que estas dos integrales son iguales si las funciones son reales.

Colaboradores y Atribuciones

• Adapted from "Quantum States of Atoms and Molecules" by David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski