10.5: La aproximación de electrones PI de la conjugación
- Page ID
- 79709
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Demostrar cómo la teoría de Hückel se aproxima a la imagen orbital molecular completa de las moléculas mediante el tratamiento\(\sigma\) de las redes de unión y\(\pi\) unión de forma independiente.
La teoría orbital molecular se ha aplicado con mucho éxito a grandes sistemas conjugados, especialmente aquellos que contienen cadenas de átomos de carbono con enlaces simples y dobles alternantes. Una aproximación introducida por Hückel en 1931 considera solo los electrones p deslocalizados que se mueven en un marco\(\pi\) de enlaces. Esta es, de hecho, una versión más sofisticada de un modelo de electrones libres.
El hidrocarburo más simple a considerar que exhibe\(\pi\) enlace es el etileno (eteno), el cual está compuesto por cuatro átomos de hidrógeno y dos átomos de carbono. Experimentalmente, sabemos que los ángulos H-C—H y H-C-C en etileno son aproximadamente 120°. Este ángulo sugiere que los átomos de carbono son sp 2 hibridados, lo que significa que un orbital sp 2 ocupado individualmente sobre un carbono se solapa con un orbital s ocupado individualmente en cada H y un lóbulo sp 2 ocupado individualmente en el otro C. Así, cada carbono forma un conjunto de tres\(\sigma\) enlaces: dos C—H (sp 2 + s) y uno C—C (sp 2 + sp 2) (parte (a) de la Figura 10.5.1 ).
La aproximación de Hückel se utiliza para determinar las energías y formas de los orbitales\(\pi\) moleculares en sistemas conjugados. Dentro de la aproximación de Hückel, el enlace covalente en estos hidrocarbonas se puede separar en dos “marcos” independientes: el marco de\(\sigma\) enlace y el marco\(\sigma\) de unión. Las funciones de onda utilizadas para describir los orbitales de unión en cada marco resultan de diferentes combinaciones de orbitales atómicos. El método se limita a abordar hidrocarburos conjugados y específicamente solo se incluyen orbitales moleculares de\(\pi\) electrones porque estos determinan las propiedades generales de estas moléculas; se ignoran los electrones sigma. Esto se conoce como separabilidad sigma-pi y se justifica por la ortogonalidad de\(\sigma\) y\(\pi\) orbitales en moléculas planas. Por esta razón, el método de Hückel se limita a sistemas planos. La aproximación de Hückel asume que los electrones en los\(\pi\) enlaces “sienten” un potencial electrostático debido a todo el marco de\(\sigma\) unión en la molécula (es decir, se enfoca solo en la formación de\(\pi\) enlaces, dado que el marco de\(\sigma\) unión ya se ha formado).
Un sistema conjugado tiene una región de orbitales p superpuestos, que une los enlaces simples interyacentes, que permiten una deslocalización de\(\pi\) electrones a través de todos los orbitales p alineados adyacentes. Estos\(\pi\) electrones no pertenecen a un enlace sencillo o átomo, sino a un grupo de átomos.
Etileno
Antes de considerar el tratamiento de Hückel para etileno, es beneficioso revisar el cuadro general de unión de la molécula. La unión en etileno implica la\(sp^2\) hibridación de los orbitales\(2s\)\(2p_x\),, y\(2p_y\) atómicos en cada átomo de carbono; dejando los\(2p_z\) orbitales intactos (Figura 10.5.2 ).
El uso de orbitales híbridos en el enfoque orbital molecular descrito aquí es meramente una conveniencia y no invocar la teoría del enlace de valencia (directamente). Se puede extraer una descripción idéntica utilizando exclusivamente orbitales atómicos sobre carbono, pero la interpretación de las funciones de onda resultantes es menos intuitiva. Por ejemplo, el i-ésimo orbital molecular se puede describir a través de orbitales híbridos
\[ | \psi_1\rangle = c_1 | sp^2_1 \rangle + c_2 | 1s_a \rangle \nonumber \nonumber \]
o vía orbitales atómicos.
\[ | \psi_1\rangle = a_1 | 2s \rangle + a_1 | 2p_x \rangle + a_1 | 2p_y \rangle + a_4| 1s_a \rangle \nonumber \nonumber \]
donde\(\{a_i\}\) y\(\{c_i\}\) son coeficientes de la expansión. Cualquiera de los dos describirán funcionará y ambos son enfoques idénticos ya que
\[| sp^2_1 \rangle = b_1 | 2s \rangle + b_1 | 2p_x \rangle + b_1 | 2p_y \rangle \nonumber \nonumber \]
donde\(\{c_i\}\) están los coeficientes que describen el orbital hibridado.
El enlace se produce a través de la mezcla de los electrones en los orbitales\(sp^2\) híbridos sobre el carbono y los electrones en los orbitales\(1s\) atómicos de los cuatro átomos de hidrógeno (Figura 10.5.1 ; izquierda) dando como resultado el marco de\(\sigma\) unión. El marco\(\pi\) de unión es el resultado de\(2p_z\) los orbitales no hibridados (Figura 10.5.2 ; derecha). La independencia de estos dos marcos se demuestra en el diagrama orbital molecular resultante en la Figura 10.5.3 ; la teoría de Hückel se ocupa únicamente de describir los orbitales moleculares y las energías del marco de\(\pi\) unión.
El tratamiento de Hückel se ocupa únicamente de describir los orbitales moleculares y las energías del marco de\(\pi\) unión.
Dado que la teoría de Hückel es una consideración especial de la teoría orbital molecular, los orbitales moleculares\(| \psi_i \rangle\) pueden describirse como una combinación lineal de los orbitales\(2p_z\) atómicos\(\phi\) en carbono con sus\(\{c_i\}\) coeficientes correspondientes:
\[ | \psi_i \rangle =c_1 | \phi_{1} \rangle +c_2 | \phi_2 \rangle \label{LCAO} \]
Esta ecuación se sustituye en la ecuación de Schrödinger:
\[ \hat{H} | \psi_i \rangle =E_i | \psi_i \rangle \nonumber \]
con\(\hat{H}\) el hamiltoniano y\(E_i\) la energía correspondiente al orbital molecular para dar:
\[ \hat{H} c_{1} | \phi _{1} \rangle +\hat{H} c_{2} | \phi _{2} \rangle =E c_{1} | \phi _{1} \rangle +E c_{2} | \phi _{2} \rangle \label{SEq} \]
Si Ecuación\(\ref{SEq}\) se multiplica por\(\langle \phi _{1}| \) (e integra), entonces
\[c_1(H_{11} - ES_{11}) + c_2(H_{12} - ES_{12}) = 0 \label{Eq1} \]
donde\( H_{ij}\) están los elementos de la matriz hamiltoniana (ver nota abajo)
\[ H_{ij} = \langle \phi_i | \hat{H} | \phi_j \rangle = \int \phi _{i}H\phi _{j}\mathrm {d} v\nonumber \]
y\( S_{ij} \) son las integrales superpuestas.
\[ S_{ij}= \langle \phi_i | \phi_j \rangle = \int \phi _{i}\phi _{j}\mathrm {d} v\nonumber \]
Si Ecuación\(\ref{SEq}\) se multiplica por\( \langle \phi _{2} | \) (e integra), entonces
\[c_1(H_{21} - ES_{21}) + c_2(H_{22} - ES_{22}) = 0 \label{Eq2} \]
Ambas ecuaciones\(\ref{Eq1}\) y\(\ref{Eq2}\) pueden representarse mejor en notación matricial,
\[ {\begin{bmatrix}c_{1}(H_{11}-ES_{11})+c_{2}(H_{12}-ES_{12})\\c_{1}(H_{21}-ES_{21})+c_{2}(H_{22}-ES_{22})\\\end{bmatrix}}=0\nonumber \]
o más simplemente como producto de matrices.
\[\begin{bmatrix} H_{11} - ES_{11} & H_{12} - ES_{12} \\ H_{21} - ES_{21} & H_{22} - ES_{22} \\ \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ \end{bmatrix}= 0 \label{master} \]
Todas las integrales hamiltonianas diagonales\( H_{ii}\) se llaman integrales de Coulomb y las de tipo\(H_{ij}\) se llaman integrales de resonancia. Ambas integrales son negativas y las integrales de resonancia determinan la fuerza de las interacciones de unión. Las ecuaciones descritas por Ecuación se\(\ref{master}\) denominan ecuaciones seculares y también tendrán la solución trivial de
\[ c_1 = c_2 = 0 \nonumber \]
Dentro del álgebra lineal, las ecuaciones seculares en Ecuación también\(\ref{master}\) tendrán una solución no trivial, si y solo si, el determinante secular es cero
\[ \left| \begin{array} {cc} H_{11} - ES_{11} & H_{12} - ES_{12} \\ H_{21} - ES_{21} & H_{22} - ES_{22} \\ \end{array}\right| = 0 \label{SecDet} \]
o en notación taquigráfica
\[ \text{det}(H -ES) =0\nonumber \]
Todo en Ecuación\(\ref{SecDet}\) es un número conocido excepto\(E\). Dado que el determinante secular para el etileno es una\(2 \times 2\) matriz, encontrar\(E\), requiere resolver una ecuación cuadrática (después de expandir el determinante)
\[ ( H_{11} - ES_{11} ) ( H_{22} - ES_{22} ) - ( H_{21} - ES_{21} )( H_{12} - ES_{12} ) = 0\nonumber \]
Habrá dos valores de los\(E\) cuales satisfacen esta ecuación y son las energías orbitales moleculares. Para el etileno, una será la energía de unión y la otra la energía antiunión para los\(\pi\) orbitales formados por la combinación de los dos\(2p_z\) orbitales de carbono (Ecuación\(\ref{LCAO}\)). Sin embargo, si se utilizaran más de dos orbitales\(| \phi \rangle\) atómicos, por ejemplo, en una molécula más grande, entonces se estimarían más energías resolviendo el determinante secular.
La solución del determinante secular se simplifica dentro del método de Hückel a través de los siguientes cuatro supuestos:
- Todas las integrales superpuestas\(S_{ij}\) son iguales a cero. Esto es bastante razonable ya que los\(\pi-\) orbitales se dirigen perpendicularmente a la dirección de sus enlaces (Figura 10.5.1 ). Esta suposición a menudo se llama descuido de superposición diferencial (NDO).
- Todas las integrales de resonancia\(H_{ij}\) entre átomos no vecinos se establecen iguales a cero.
- Todas las integrales de resonancia\(H_{ij}\) entre los átomos vecinos son iguales y se establecen en\(\beta\).
- Todas las integrales de culombo\(H_{ii}\) se establecen iguales a\(\alpha\).
Estas suposiciones se expresan matemáticamente como
\[ H_{11}=H_{22}=\alpha\nonumber \]
\[ H_{12}=H_{21}=\beta\nonumber \]
Supuestos 1 significa que la integral de superposición entre los dos orbitales atómicos es 0
\[ S_{11}=S_{22}=1\nonumber \]
\[ S_{12}=S_{21}=0\nonumber \]
Las integrales de Coulomb
\[H_{ii}= \langle \phi _i|H| \phi _i \rangle \nonumber \nonumber \]
e integrales de resonancia.
\[H_{ij}= \langle \phi _i|H| \phi _j \rangle \,\,\, (i \neq i) \nonumber \nonumber \]
se describen a menudo dentro de la representación matricial de los hamiltonianos (específicamente dentro de la\( | \phi \rangle\) base):
\[ \hat{H} = \begin{bmatrix} H_{11} & H_{12} \\ H_{21} & H_{22} \end {bmatrix} \nonumber \nonumber \]
o dentro de los supuestos de Hückel
\[ \hat{H} = \begin{bmatrix} \alpha & \beta \\ \beta & \alpha \end {bmatrix} \nonumber \nonumber \]
Los supuestos de Hückel reducen la ecuación\(\ref{master}\) en dos ecuaciones homogéneas:
\[\begin{bmatrix} \alpha - E & \beta \\ \beta & \alpha - E \\ \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ \end{bmatrix}= 0 \label{Eq12} \]
si la ecuación\(\ref{Eq12}\) se divide por\(\beta\):
\[\begin{bmatrix} \dfrac{\alpha - E}{\beta} & 1 \\ 1 & \dfrac{\alpha - E}{\beta} \\ \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ \end{bmatrix}= 0\nonumber \]
y luego se define una nueva variable\(x\)
\[ x = \dfrac {\alpha -E}{\beta} \label{new} \]
entonces Ecuación\(\ref{Eq12}\) simplifica a
\[\begin{bmatrix} x & 1 \\ 1 & x \\ \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ \end{bmatrix}= 0 \label{seceq} \]
La solución trivial da ambos coeficientes de función de onda iguales a cero y la otra solución (no trivial) se determina resolviendo el determinante secular
\[ \begin{vmatrix}x&1\\1&x\\\end{vmatrix}=0\nonumber \]
que cuando se expande es\(x^{2}-1=0\) así\( x=\pm 1\).
Sabiendo que\(E=\alpha -x\beta \) a partir de la ecuación\(\ref{new}\), se puede encontrar que los niveles de energía son
\[ E=\alpha -\pm 1\times \beta \nonumber \]
o
\[ E=\alpha \mp \beta \nonumber \]
Como\(\beta\) es negativo, se ordenan las dos energías (Figura 10.5.4 )
- Para\(\pi_1\):\(E_1 =\alpha + \beta\)
- Para\(\pi_2\):\(E_2 =\alpha - \beta\)
Para extraer los coeficientes atribuidos a estas energías, los\(x\) valores correspondientes pueden ser sustituidos de nuevo en las Ecuaciones Seculares (Ecuación\(\ref{seceq}\)). Para el estado de menor energía (\(x=-1\))
\[\begin{bmatrix} -1 & 1 \\ 1 & -1 \\ \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ \end{bmatrix}= 0 \nonumber \]
Esto da\(c_1=c_2\) y los orbitales moleculares atribuidos a esta energía son entonces (basados en la Ecuación\(\ref{LCAO}\)):
\[ |\psi_1 \rangle = N_1 (\phi_1 \rangle + | \phi_2 \rangle ) \label{HOMO} \]
donde\(N_1\) está la constante de normalización para este orbital molecular; este es el orbital molecular de unión.
Para el orbital molecular de mayor energía (\(x=-1\)) y luego
\[\begin{bmatrix} 1 & 1 \\ 1 & 1 \\ \end{bmatrix} \times \begin{bmatrix} c_1 \\ c_2 \\ \end{bmatrix}= 0 \nonumber \]
Esto da\(c_1=-c_2\) y los orbitales moleculares atribuidos a esta energía son entonces (basados en la Ecuación\(\ref{LCAO}\)):
\[ \psi_2 \rangle = N_2 (\phi_1 \rangle - | \phi_2 \rangle ) \label{LUMO} \]
donde\(N_2\) está la constante de normalización para este orbital molecular; este es el orbital molecular antienlace.
Las constantes de normalización para ambos orbitales moleculares se pueden obtener mediante el enfoque de normalización estándar (es decir,\(\langle \psi_i | \psi_i \rangle =1\)) para obtener
\[N_1 = N_2 = \dfrac{1}{\sqrt{2}}\nonumber \]
Estos orbitales moleculares forman el marco de\(\pi\) unión y como cada carbono aporta un electrón a este marco, solo se ocupa el orbital molecular más bajo (\( | \psi_1 \rangle\)) (Figura 10.5.5 ) en el estado fundamental. La configuración electrónica correspondiente es entonces\( \pi_1^2\).
HOMO y LUMO son siglas de orbital molecular ocupado más alto y orbital molecular desocupado más bajo, respectivamente y a menudo se denominan orbitales fronterizos. La diferencia de energía entre HOMO y LUMO se denomina brecha HOM O—LUMO.
Los orbitales\(\pi\) moleculares calculados en 3-D se muestran en la Figura 10.5.6 .

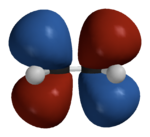
La teoría de Hückel se desarrolló en la década de 1930 cuando las computadoras no estaban disponibles y los enfoques matemáticos simples eran muy importantes para comprender el experimento. Aunque los supuestos en la teoría de Hückel son drásticos, permitieron que los primeros cálculos de orbitales moleculares se realizaran con calculadoras mecánicas o a mano. La Teoría de Hückel se puede extender para abordar otros tipos de átomos en moléculas conjugadas (por ejemplo, nitrógeno y oxígeno). Además, se puede extender para tratar también\(\sigma\) orbitales y esta “Teoría Extendida de Hückel” todavía se usa hoy en día. A pesar de la utilidad de la Teoría de Hückel, es altamente cualitativa y debemos recordar las limitaciones de la Teoría de Hückel:
- La teoría de Hückel es muy aproximada
- La teoría de Hückel no puede calcular las energías con precisión (no se calcula la repulsión electrón-electrón)
- La teoría de Hückel suele sobreestimar los momentos dipolares predichos
La teoría de Hückel se usa mejor para proporcionar modelos simplificados para comprender la química y para una comprensión detallada se necesitan métodos moleculares ab initio modernos discutidos en el Capítulo 11.
Colaboradores
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)
- Wikipedia
- StackExchange (Philipp)

