12.4: Operaciones de simetría como matrices

Las matrices se pueden utilizar para mapear un conjunto de coordenadas o funciones en otro conjunto. Las matrices utilizadas para este propósito se denominan matrices de transformación. En la teoría de grupos, podemos utilizar matrices de transformación para llevar a cabo las diversas operaciones de simetría discutidas anteriormente. Como ejemplo sencillo, investigaremos las matrices que usaríamos para llevar a cabo algunas de estas operaciones de simetría sobre un vector en el espacio 2D\(\begin{pmatrix} x, y \end{pmatrix}\).

La matriz de transformación para cualquier operación en un grupo tiene una forma que es única de las matrices de los otros miembros del mismo grupo; sin embargo, el carácter de la matriz de transformación para una operación dada es el mismo que para cualquier otra operación de la misma clase.

Cada operación de simetría a continuación operará en un vector arbitrario:

\[ \bf{u} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\]

La Operación Identidad,\(E\)

El operador de identidad,\(E\), leaves the vector unchanged, and as you may already suspect, the appropriate matrix is the identity matrix:

\[ E\bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \label{9.1} \]

La Operación Reflexión,\(\sigma\)

La operación de reflexión refleja el vector\(\bf{u}\) sobre un plano. Esto puede ser el\(xy\),\(xz\), o\(yz\) avión. La matriz es similar a la matriz de identidad, con la excepción de que existe un cambio de signo para el elemento apropiado. La matriz de reflexión en el\(xy\) plano es:

\[ \sigma \bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ y \\ -z \end{pmatrix} \label{9.2} \]

Observe que el elemento para la dimensión que se refleja es el on que es negativo. En el caso anterior, ya que\(z\) se está reflejando sobre el\(xy\) plano, el\(z\) elemento en la matriz es negativo. Si tuviéramos que reflexionar sobre el\(xz\) plano en su lugar, el\(y\) elemento sería el que es negativo:

\[ \sigma \bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ -y \\ z \end{pmatrix} \]

También podemos hablar de reflexiones en 2 dimensiones. El ejemplo más simple de una matriz de reflexión corresponde a reflejar el vector\(\begin{pmatrix} x, y \end{pmatrix}\) in either the \(x\) or \(y\) axes. Reflection in the \(x\) axis maps \(y\) to \(-y\), while reflection in the \(y\) axis maps \(x\) to \(-x\). The appropriate matrix is very like the identity matrix but with a change in sign for the appropriate element. Reflection in the \(x\) axis transforms the vector \(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} x, -y \end{pmatrix}\), and the appropriate matrix is

\[  \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \\ -y \end{pmatrix} \]

Figura 12.4.1 : Reflexión a través del eje x en el espacio 2D.

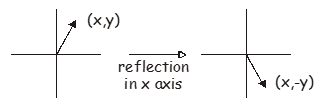
La reflexión en el eje y transforma el vector\(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} -x, y \end{pmatrix}\), and the appropriate matrix is:

\[ \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -x \\ y \end{pmatrix} \label{9.3} \]

Figura 12.4.2 : Reflexión a través del eje y en el espacio 2D.

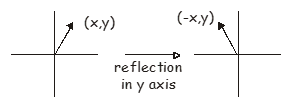
De manera más general, las matrices se pueden usar para representar reflexiones en cualquier plano (o línea en 2D). Por ejemplo, reflexión en el eje de 45° que se muestra a continuación mapas\(\begin{pmatrix} x, y \end{pmatrix}\) onto \(\begin{pmatrix} -y, -x \end{pmatrix}\).

\[ \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -y \\ -x \end{pmatrix} \label{9.4} \]

Figura 12.4.3 : Reflexión a través del eje que se gira 45 ° con respecto al eje x en el espacio 2D.

La operación de rotación\(n\) -fold,\(C_n\)

La rotación en sentido antihorario\(z\) es:

\ [C_n\ bf {u} =\ begin {pmatrix}\ cos {\ frac {2\ pi} {n}} & -\ sin {\ frac {2\ pi} {n}} & 0\\ sin {\ frac {2\ pi} {n}} &\ cos {\ frac {2\ pi} {n}} & 0\ 0 y 1\ end {pmatrix}
\ begin {pmatrix} x\\ y\\ z\ end {pmatrix} =
\ begin {pmatrix} x'\\ y'\\ z\ end {pmatrix}\]

Para la rotación en sentido horario, el signo en los\(\sin{\theta}\) términos se invertirá. Esta matriz simplifica drásticamente para la\(C_2\) rotación:

\ [C_2\ bf {u} =\ begin {pmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 0 & 1\ end {pmatrix}
\ begin {pmatrix}\\ y\\ z\ end {pmatrix} =
\ begin {pmatrix} -x\\ -y\\ z\ end {pmatrix}\]

rotaciones sobre el\(x\), \(y\) and \(z\) axes acting on a vector \(\begin{pmatrix} x, y, z \end{pmatrix}\) are represented by the following matrices.

\[R_{x}(\theta) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix} \label{9.6a} \]

\[R_{y}(\theta) = \begin{pmatrix} \cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{pmatrix} \label{9.6b} \]

\[R_{z}(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \label{9.6c} \]

La operación de rotación también se puede realizar en dos dimensiones. En dos dimensiones, la matriz apropiada para representar la rotación por un ángulo\(\theta\) alrededor del origen es

\[R(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \label{9.5} \]

La operación de inversión,\(I\)

La operación de inversión invierte cada punto:

\ [I\ bf {u} =\ begin {pmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -1\ end {pmatrix}
\ begin {pmatrix}\ begin {pmatrix} x\\ y\\ z\ end {pmatrix} =
\ begin {pmatrix} -x\\ -y\\ -z\ end {pmatrix}\]

Inversión del 2D el vector\(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} -x, -y \end{pmatrix}\), and the appropriate matrix is:

\[ \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -x \\ -y \end{pmatrix} \]

\(C_{2v}\)Grupo de puntos

Ahora que hemos visto la forma matricial de nuestros operadores, podemos ver cómo la multiplicación de cada operador lleva a otras operaciones en el grupo. La tabla\(C_{2v}\) de multiplicación es:

\(C_{2v}\)	\(E\)	\(C_2\)	\(\sigma_v\)	\(\sigma_v'\)
\(E\)	\(E\)	\(C_2\)	\(\sigma_v\)	\(\sigma_v'\)
\(C_2\)	\(C_2\)	\(E\)	\(\sigma_v'\)	\(\sigma_v\)
\(\sigma_v\)	\(\sigma_v\)	\(\sigma_v'\)	\(E\)	\(C_2\)
\(\sigma_v'\)	\(\sigma_v'\)	\(\sigma_v\)	\(C_2\)	\(E\)

Veamos la\(C_2 \sigma_v\) multiplicación, donde\(\sigma_v\) hay un reflejo a través del\(xz\) plano:

\ [C_2\ sigma_v =\ begin {pmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 1\ end {pmatrix}\ begin {pmatrix} 1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 0 & 1\ end {pmatrix}
=\ begin {pmatrix} -1 & 0 & 0\\ 0 & 1 & 0\ 0 & 0 & 1\ end {pmatrix} =\ sigma_v'\]

donde\(\sigma_v'\) está el reflejo a través del\(yz\) plano.

Representación Matriz

Las operaciones de simetría en un grupo pueden ser representadas por un conjunto de matrices de transformación\(\Gamma\)\((g)\), una para cada elemento de simetría\(g\). Cada matriz individual se llama un representante de la operación de simetría correspondiente, y el conjunto completo de matrices se llama una representación matricial del grupo. Los representantes de la matriz actúan sobre alguna base elegida conjunto de funciones, y las matrices reales que componen una representación determinada dependerán de la base que se haya elegido. Entonces se dice que la representación abarca la base elegida. En los ejemplos anteriores estuvimos viendo el efecto de algunas matrices de transformación simples sobre un vector arbitrario\(\begin{pmatrix} x, y \end{pmatrix}\). Por lo tanto, la base es un par de vectores unitarios que apuntan en las\(y\) direcciones\(x\) y. En el espacio 3D, la base es el conjunto de vectores unitarios que apuntan en las\(z\) direcciones\(x\)\(y\), y. En la mayoría de los ejemplos que estaremos considerando en este curso, utilizaremos conjuntos de orbitales atómicos como funciones base para representaciones matriciales. Antes de continuar, debemos comprobar que una representación matricial de un grupo obedece a todas las reglas establecidas en la definición matemática formal de un grupo.

1. Identidad. La primera regla es que el grupo debe incluir la operación de identidad\(E\) (la operación de 'no hacer nada'). Se demostró anteriormente que la matriz representativa de la operación de identidad es simplemente la matriz de identidad. Como consecuencia, cada representación matricial incluye la matriz de identidad apropiada.
2. Cierre. La segunda regla es que la combinación de cualquier par de elementos también debe ser un elemento del grupo (la propiedad group). Si multiplicamos dos representantes de matriz cualesquiera, deberíamos obtener una nueva matriz que sea representativa de otra operación de simetría del grupo. De hecho, los representantes de la matriz se multiplican para dar nuevos representantes exactamente de la misma manera que las operaciones de simetría se combinan de acuerdo con la tabla de multiplicación grupal. Por ejemplo, en el grupo de\(C_{2v}\) puntos, mostramos que la operación de simetría combinada\(C_2\)\(\sigma_v\) es equivalente a \(\sigma_v'\). En una representación matricial del grupo, si los representantes matriciales de\(C_2\) y \(\sigma_v\)se multiplican juntos, el resultado será el representativo de \(\sigma_v'\).
3. Asociatividad. La tercera regla establece que la regla de combinación de elementos de simetría en un grupo debe ser asociativa. Esto es automáticamente satisfecho por las reglas de multiplicación matricial.
3. Reciprocalidad. La regla final establece que toda operación debe tener una inversa, que también es miembro del grupo. El efecto combinado de realizar una operación y su inversa es el mismo que la operación de identidad. Es bastante fácil demostrar que los representantes de la matriz satisfacen este criterio. Por ejemplo, la inversa de una reflexión es otra reflexión, idéntica a la primera. En términos de matriz, por lo tanto, esperaríamos que una matriz de reflexión fuera su propia inversa, y que dos matrices de reflexión idénticas multiplicadas juntas darían la matriz de identidad. Esto resulta ser cierto, y se puede verificar usando cualquiera de las matrices de reflexión en los ejemplos anteriores. El inverso de una matriz de rotación es otra matriz de rotación correspondiente a una rotación del sentido opuesto a la primera.

Ejemplo 12.4.1 : Representación matricial de la\(C_{2v}\) Point Group (the allyl radical)

En este ejemplo, tomaremos como base una\(p\) orbital on each carbon atom \(\begin{pmatrix} p_1, p_2, p_3 \end{pmatrix}\).

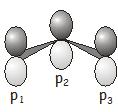
Tenga en cuenta que el\(p\) orbitals are perpendicular to the plane of the carbon atoms (this may seem obvious, but if you’re visualizing the basis incorrectly it will shortly cause you a not inconsiderable amount of confusion). The symmetry operations in the \(C_{2v}\) point group, and their effect on the three \(p\) orbitals, are as follows:

\ [\ begin {array} {ll} E &\ begin {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix}\ rightarrow\ begin {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix}\\
C_2 &\ begin {pmatrix} p_1\ p_2\\ p_3\ end {pmatrix}\ Rightarrow\ begin {pmatrix} -p_3\\ -p_2\\ -p_1\ end {pmatrix}\\
\ sigma_v &\ comenzar {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix}\ rightarrow\ begin {pmatrix} -p_1\\ -p_2\\ -p_3\ end {pmatrix}\
\ sigma_v' &\ begin {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix}\ rightarrow\ begin {pmatrix matrix} p_1\\ p_2\\ p_3\ end {pmatrix}\ end {array}\ nonumber\]

Las matrices que llevan a cabo la transformación son

\ [\ begin {array} {ll}\ Gamma (E) &\ begin {pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\ end {pmatrix}\ begin {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix} =\ begin {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix} matriz}\\
\ Gamma (C_2) &\ begin {pmatrix} 0 & 0 & -1\\ 0 & -1 & 0\\ -1 & 0 & 0\ end {pmatrix}\ begin {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix} =\ begin {pmatrix} -p_3\\ -p_2\\ -p_1\ end {pmatrix}\\
\ Gamma (\ sigma_v) &\ begin {pmatrix} -1 & 0 & 0\ 0 & -1 & 0\\ 0 & 0 & -1\ end {pmatrix}\ begin {pmatrix} p_1\\ p_2\\ p_3\ end { pmatrix} =\ begin {pmatrix} -p_1\\ -p_2\\ -p_3\ end {pmatrix}\\
\ Gamma (\ sigma_v') &\ begin {pmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 & 0\ end {pmatrix}\ begin {pmatrix} p_1\ p_2\\ p_3\ end {pmatrix} =\ begin {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix}\ end {matriz}\ end {array}\ nonumber \]

Hemos escrito los vectores que representan nuestra base como vectores de fila. Esto es importante. Si las hubiéramos escrito como vectores de columna, las matrices de transformación correspondientes serían las transpuestas de las matrices anteriores, y no reproducirían la tabla de multiplicación grupal (pruébalo como ejercicio si necesitas convencerte).