Al hacer espectroscopía de RMN, es un hecho observado que los hidrógenos equivalentes no se dividen entre sí. ¿Por qué los hidrógenos equivalentes no dividen las señales de los demás? Por ejemplo, ¿por qué el espectro de RMN para etano es un singlete en lugar de un cuarteto o incluso un dodecuplete (debido a los hidrógenos en el mismo carbono)? ¿Qué tiene de especial que los hidrógenos sean equivalentes entre sí que no provoca que se observe división alguna?
Encontrar los estados entre los que ocurren las transiciones
El hamiltoniano para dos giros acoplados es
\[\hat{H} = \omega_1\hat{I}_{\!1z} + \omega_2\hat{I}_{\!2z} + \dfrac{2\pi J_{12}}{\hbar}(\hat{\vec{I}_{\!1}}\cdot\hat{\vec{I}_{\!2}}) \label{1} \]
donde\(\omega_1\) y\(\omega_2\) son las frecuencias Larmor [2] de los dos núcleos y\(J_{12}\) es la constante de acoplamiento (en Hz) entre los dos núcleos. (El factor de simplemente\(2\pi/\hbar\) está ahí para llevarlo a las unidades de energía.) \(\hat{I}_{\!i}\)es el operador para el momento angular de giro del núcleo\(i\) y\(\hat{I}_{\!iz}\) es el operador para su proyección a lo largo del\(z\) eje.
Sin embargo, en RMN, se acostumbra trabajar en unidades de frecuencia en lugar de unidades de energía. Ya que\(E = h\nu\), simplemente necesitamos dividirnos por\(h\). Teniendo en cuenta eso\(\omega = 2\pi\nu\) y\(h = 2\pi\hbar\), obtenemos:
\[\hat{H}_\text{freq} = \dfrac{\nu_1}{\hbar}\hat{I}_{\!1z} + \dfrac{\nu_2}{\hbar}\hat{I}_{\!2z} + \dfrac{J_{12}}{\hbar^2}(\hat{\vec{I}_{\!1}}\cdot\hat{\vec{I}_{\!2}}) \label{2} \]
Encima de eso, para facilitar las matemáticas, también es bastante común establecer\(\hbar = 1\). Por lo tanto, tenemos
\[\hat{H}_\text{freq} = \nu_1\hat{I}_{\!1z} + \nu_2\hat{I}_{\!2z} + J_{12}(\hat{\vec{I}_{\!1}}\cdot\hat{\vec{I}_{\!2}}) \label{3} \]
Trataremos con dos\(1/2\) núcleos de giro aquí, donde\(|\alpha\rangle\) y\(|\beta\rangle\) representaremos los giros “arriba” y “abajo” (recordamos\(\hbar = 1\) que establecemos para que no aparezca en los valores propios):
\[\begin{align*} \hat{I}_{\!iz}|\alpha_i\rangle &= \dfrac{1}{2}|\alpha_i\rangle & \hat{I}_{\!iz}|\beta_i\rangle &= -\dfrac{1}{2}|\beta_i\rangle & (i = 1,2) \label{4} \end{align*} \]
Además, dado que estamos tratando con núcleos equivalentes, simplemente podemos establecer\(\nu_1 = \nu_2 = \nu\) y soltar el subíndice\(J_{12}\) solo para hacerlo un poco más limpio:
\[\hat{H} = \nu(\hat{I}_{\!1z} + \hat{I}_{\!2z}) + J(\hat{\vec{I}_{\!1}}\cdot\hat{\vec{I}_{\!2}}) \label{5} \]
Ahora, necesitamos encontrar los autoestados y los valores propios de\(\hat{H}\). Para ello, adoptaremos el conjunto básico de funciones del producto\((|\alpha_1\alpha_2\rangle, |\alpha_1\beta_2\rangle, |\beta_1\alpha_2\rangle, |\beta_1\beta_2\rangle)\). De la ecuación\((4)\) tenemos
\[\begin{align*} \hat{I}_{\!1z}|\alpha_1\alpha_2\rangle &= \dfrac{1}{2}|\alpha_1\alpha_2\rangle & \hat{I}_{\!2z}|\alpha_1\alpha_2\rangle &= \dfrac{1}{2}|\alpha_1\alpha_2\rangle \label{6} \\ \hat{I}_{\!1z}|\alpha_1\beta_2\rangle &= \dfrac{1}{2}|\alpha_1\beta_2\rangle & \hat{I}_{\!2z}|\alpha_1\beta_2\rangle &= -\dfrac{1}{2}|\alpha_1\beta_2\rangle \label{7} \\ \hat{I}_{\!1z}|\beta_1\alpha_2\rangle &= -\dfrac{1}{2}|\beta_1\alpha_2\rangle & \hat{I}_{\!2z}|\beta_1\alpha_2\rangle &= \dfrac{1}{2}|\beta_1\alpha_2\rangle \label{8} \\ \hat{I}_{\!1z}|\beta_1\beta_2\rangle &= -\dfrac{1}{2}|\beta_1\beta_2\rangle & \hat{I}_{\!2z}|\beta_1\beta_2\rangle &= -\dfrac{1}{2}|\beta_1\beta_2\rangle \label{9} \end{align*} \]
La acción del producto escalar\(\hat{\vec{I}_{\!1}}\cdot\hat{\vec{I}_{\!2}}\) es más complicada. Necesitamos introducir los operadores de turno (o operadores de escalera).
\[\begin{align*} \hat{I}_{\!i+} &= \hat{I}_{\!ix} + \mathrm{i}\hat{I}_{\!iy} & \hat{I}_{\!i-} &= \hat{I}_{\!ix} - \mathrm{i}\hat{I}_{\!iy} \label{10} \end{align*} \]
de la que podemos obtener
\[\begin{align*} \hat{I}_{\!ix} &= \dfrac{\hat{I}_{\!i+} + \hat{I}_{\!i-}}{2} & \hat{I}_{\!iy} &= \dfrac{\hat{I}_{\!i+} - \hat{I}_{\!i-}}{2\mathrm{i}} \label{11} \end{align*} \]
Entonces, finalmente, podemos escribir
\[\begin{align*} \hat{\vec{I}_{\!1}}\cdot\hat{\vec{I}_{\!2}} &= \hat{I}_{\!1x}\hat{I}_{\!2x} + \hat{I}_{\!1y}\hat{I}_{\!2y} + \hat{I}_{\!1z}\hat{I}_{\!2z} \label{12} \\ &= \dfrac{\hat{I}_{\!1+}\hat{I}_{\!2-} + \hat{I}_{\!1-}\hat{I}_{\!2+}}{2} + \hat{I}_{\!1z}\hat{I}_{\!2z} \label{13} \end{align*} \]
donde al pasar de\((12)\) a\((13)\) uno simplemente sustituye\((11)\) y hace un poco de manipulación algebraica. La acción de los operadores de turno son
\ [\ comenzar {alinear*}
\ sombrero {yo} _ {\! i+} |\ alpha_i\ rangle &= 0 &\ hat {I} _ {\! i+} |\ beta_i\ rangle &= |\ alpha_i\ rangle\ tag {14}\\
\ hat {I} _ {\! i-} |\ alpha_i\ rangle &= |\ beta_i\ rangle &\ hat {I} _ {\! i-} |\ beta_i\ rangle &= 0\ tag {14}\\
\ end {align*}\ nonumber\]
Esto le permite calcular el efecto de\(\hat{\vec{I}_{\!1}}\cdot\hat{\vec{I}_{\!2}}\) sobre nuestra base estados. La matemática real se deja al lector y simplemente citaré los resultados:
\[\begin{align*} \hat{H}|\alpha_1\alpha_2\rangle &= \left(\nu + \dfrac{J}{4}\right)|\alpha_1\alpha_2\rangle \label{15} \\ \hat{H}|\alpha_1\beta_2\rangle &= -\dfrac{J}{4}|\alpha_1\beta_2\rangle + \dfrac{J}{2}|\beta_1\alpha_2\rangle \label{16} \\ \hat{H}|\beta_1\alpha_2\rangle &= \dfrac{J}{2}|\alpha_1\beta_2\rangle - \dfrac{J}{4}|\beta_1\alpha_2\rangle \label{17} \\ \hat{H}|\beta_1\beta_2\rangle &= \left(-\nu + \dfrac{J}{4}\right)|\beta_1\beta_2\rangle \label{18} \\ \end{align*} \]
Por lo tanto, en esta base la matriz hamiltoniana es
\[\mathbf{H} = \begin{pmatrix} \nu + J/4 & 0 & 0 & 0 \\ 0 & -J/4 & J/2 & 0 \\ 0 & J/2 & -J/4 & 0 \\ 0 & 0 & 0 & -\nu + J/4 \end{pmatrix} \label{19} \]
Encontrar los vectores propios y los valores propios de esta matriz se deja nuevamente al lector (no es una tarea difícil) y son (valores propios denotados\ (e_i$)
\[\begin{align*} |1\rangle &= |\alpha_1\alpha_2\rangle & E_1 &= \nu + \dfrac{J}{4} \label{20} \\ |2\rangle &= \dfrac{1}{\sqrt{2}}(|\alpha_1\beta_2\rangle + |\beta_1\alpha_2\rangle) & E_2 &= \dfrac{J}{4} \label{21} \\ |3\rangle &= \dfrac{1}{\sqrt{2}}(|\alpha_1\beta_2\rangle - |\beta_1\alpha_2\rangle) & E_3 &= -\dfrac{3J}{4} \label{22} \\ |4\rangle &= |\beta_1\beta_2\rangle & E_4 &= -\nu + \dfrac{J}{4} \label{23} \\ \end{align*} \]
La forma de los autoestados debería ser familiar: son simplemente los estados triplete y singlete de dos partículas espin-$1/2\). Estos estados surgen del acoplamiento de dos fuentes de momento angular,\(I_1\) y\(I_2\), para formar un momento angular general denotado\(I\).
\[\vec{I} = \vec{I}_{\!1} + \vec{I}_{\!2} \label{24} \]
Los valores permitidos de\(I\) están determinados por la serie Clebsch-Gordan:
\[I = I_1 + I_2, I_1 + I_2 - 1, \cdots, |I_1 - I_2| \label{25} \]
Ya que\(I_1 = I_2 = 1/2\),\(I\) puede tomar los valores\(1\) y\(0\). Los valores de\(M_I\), la proyección del momento angular total a lo largo del eje\ (z$-eje, son como de costumbre
\[M_I = I, I-1, \cdots, -I \label{26} \]
así que los estados con\(I = 1\) (“triplete”) tienen\(M_I = 1, 0, -1\) y el estado con\(I = 0\) (“singlete”) tiene\(M_I = 0\). Se puede usar más mecánica cuántica para calcular qué estado está asociado con qué números cuánticos, pero no lo haré aquí. Ellos son:
\[\begin{array}{ccc} \hline \text{State} & I & M_I \\ \hline |1\rangle & 1 & 1 \\ |2\rangle & 1 & 0 \\ |3\rangle & 0 & 0 \\ |4\rangle & 1 & -1 \\ \hline \end{array} \nonumber \]
Reglas de selección
Tenemos cuatro estados diferentes, lo que lleva a\({4\choose 2} = 6\) diferentes transiciones posibles. Sin embargo, no todas estas transiciones están permitidas.
La intensidad de la transición es proporcional al cuadrado del elemento matriz\(\langle \psi_\mathrm{f} | \hat{H'} | \psi_\mathrm{i} \rangle\) (el llamado “momento dipolar de transición”), donde\(\hat{H'}\) es el hamiltoniano para el proceso que induce la transición. En el caso de las transiciones de RMN, la transición surge debido a un campo magnético alineado a lo largo del eje\ (x$-eje. [3] Por lo tanto, el hamiltoniano correspondiente es
\[\hat{H'} = \omega'(\hat{I}_{\!1x} + \hat{I}_{\!2x}) = \omega'\hat{I}_{\!x} \label{27} \]
Exactamente lo que\(\omega'\) representa no es importante aquí porque sólo nos preocupa realmente si el momento dipolar de transición es cero o no. [4] Haciendo uso de las relaciones establecidas en las ecuaciones\ ref {10} y\ ref {11}, [5] se puede encontrar que las reglas de selección son
\[\Delta I = 0; \Delta M_I = \pm 1 \label{28} \]
lo que significa que las transiciones permitidas son\(|4\rangle \leftrightarrow |2\rangle\) y\(|2\rangle \leftrightarrow |1\rangle\). Se prohíben las transiciones hacia y desde el estado\(|3\rangle\) singlete. Las energías de las transiciones son
\[\begin{align*} E_{4\leftrightarrow2} &= \dfrac{J}{4} - \left(-\nu + \dfrac{J}{4}\right) = \nu \label{29} \\ E_{2\leftrightarrow1} &= \left(\nu + \dfrac{J}{4}\right) - \dfrac{J}{4} = \nu \label{30} \\ \end{align*} \]
es decir, las dos transiciones son degeneradas y solo se observa una línea en el espectro a\(\nu\) la frecuencia. Esto es exactamente lo que se representa en los diagramas publicados en las otras respuestas.
las dos transiciones son degeneradas y sólo se observa una línea en el espectro a\(\nu\) la frecuencia.
Notas y referencias
[1] Estoy asumiendo que el lector tiene algún conocimiento del tratamiento mecánico cuántico del momento angular, que es un tema que se trata a fondo en la mayoría de los libros de texto de mecánica cuántica. Véase, por ejemplo, el capítulo 4 de Atkins's Molecular Quantum Mechanics (5ta ed.).
[2] La frecuencia de Larmor viene dada por\(\omega = -\gamma B_0\), donde\(\gamma\) está la relación magnetogírica del núcleo en cuestión y\(B_0\) es la fuerza del campo magnético externo. Representa la frecuencia con la que un momento magnético precede alrededor de un campo magnético. Consulta cualquier libro de texto sobre magnetismo para más detalles.
[3] Estoy pasando por un lado algunos detalles aquí. El llamado campo magnético en el\(x$-axis is a component of the radiofrequency pulse applied in the \(xy\) plano. Si te interesa favor de consultar un libro de texto sobre el modelo vectorial de RMN. En particular recomiendo Keeler's Understanding NMR Spectroscopy (2a ed.).
[4] Se relaciona con la fuerza del campo magnético en el\(x\) -eje,\(B_1\), por\(w' = |\gamma|B_1\). El símbolo habitual es\(\omega_1\), pero elegí no usar esto aquí para evitar posibles confusiones. De nuevo, por favor consulte un libro de texto sobre el modelo vectorial de RMN si desea obtener más información.
[5] Una prueba completa se puede encontrar en J. Chem. Educ. 1982, 59 (10), 819. También hay cierta discusión sobre las reglas de selección en la Espectroscopia de RMN de Gunther (3a ed.), p 156 en adelante.
El primer punto importante a tener en cuenta es que los núcleos magnéticamente equivalentes de hecho se acoplan entre sí, sin embargo no se observa división en el espectro. El segundo punto es que los núcleos químicamente equivalentes, pero magnéticamente no equivalentes, se acoplan entre sí, y este acoplamiento es observable en el espectro de RMN.
El acoplamiento de espín proviene de una interacción magnética entre espines nucleares transmitidos a través de los electrones de unión. Las señales observadas en el espectro RMN son una transición entre los niveles de energía de los estados de espín permitidos. Cuando dos núcleos se 'acoplan', los niveles de energía se estabilizan o desestabilizan ligeramente en base a las orientaciones relativas de los momentos nucleares, de manera que (para un doblete) una transición es ahora δ+J/2, y la otra transición es δ-J/2. Estas dos transiciones constituyen las dos líneas de la señal doblete. Cuando dos núcleos equivalentes se acoplan, las transiciones entre niveles de energía no cambian porque las interacciones entre los momentos nucleares son las mismas, como lo son todos los demás factores contribuyentes como el contacto Fermi. Mientras las transiciones sigan siendo las mismas, todas las transiciones posibles serán equivalentes.
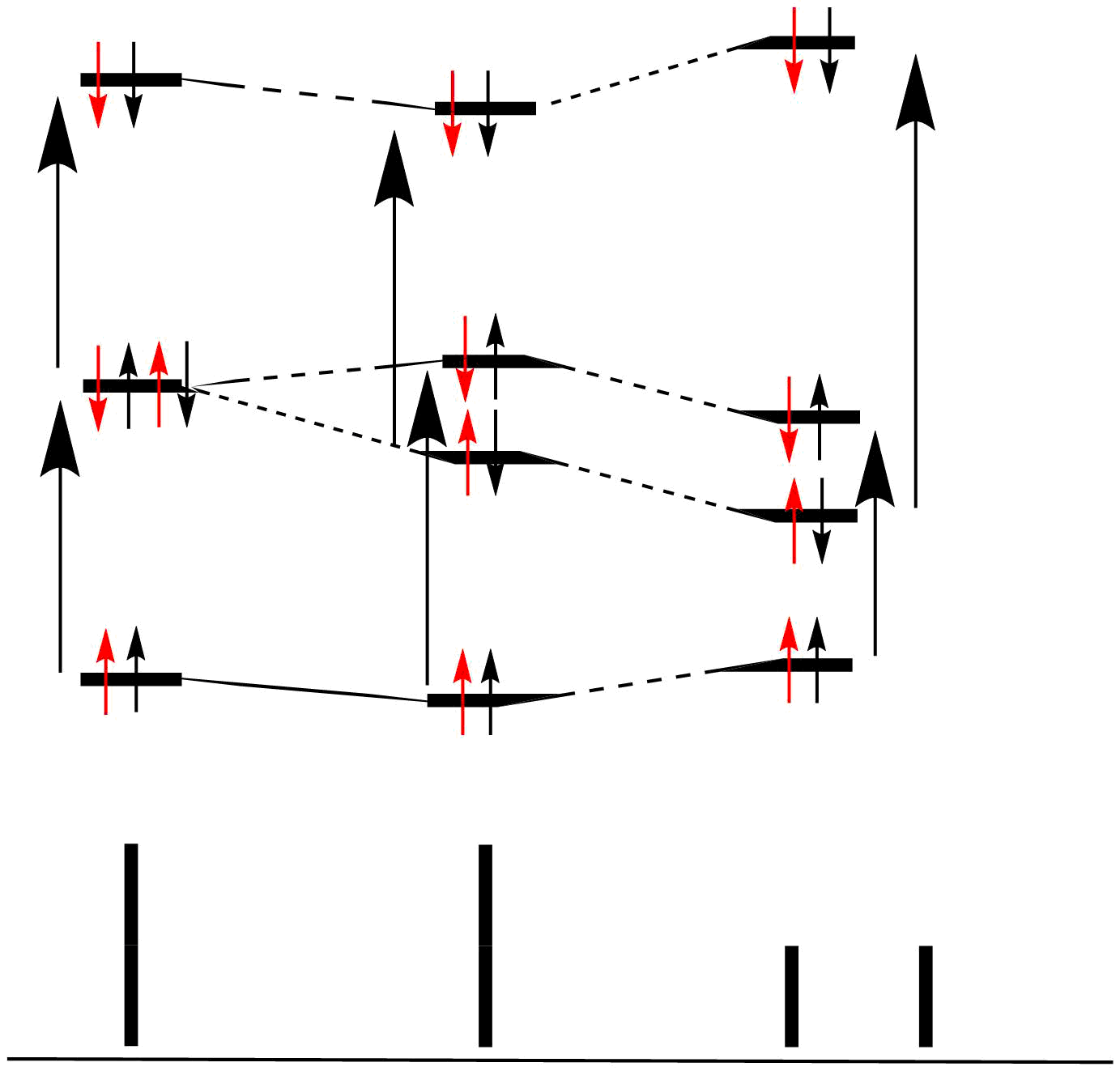
El diagrama de abajo ojalá lo explique un poco más claro. Los niveles medios de energía son para dos giros no acoplados. El giro A (mostrado en rojo) tiene dos transiciones posibles, ambas equivalentes. Cuando los dos giros están acoplados, los niveles de energía se estabilizan/desestabilizan como se muestra a la derecha. Las transiciones para el giro A ya no son equivalentes, y aparecerán como dos líneas (doblete). A la izquierda, los núcleos equivalentes tienen un cambio general en el nivel de energía, pero la transición entre los niveles sigue siendo la misma, de ahí que la línea observada siga siendo singlete.
Cuando hay dos núcleos distintos (El caso AX) y hay interacción espín-espín (\(J\)acoplamiento) entre ellos (además del desplazamiento químico) entonces se puede observar una estructura fina en el espectro de RMN. El primer diagrama muestra los niveles de energía y cómo interactúan. Observe cómo el\(J\) acoplamiento mueve los niveles hacia arriba y hacia abajo además del desplazamiento químico.
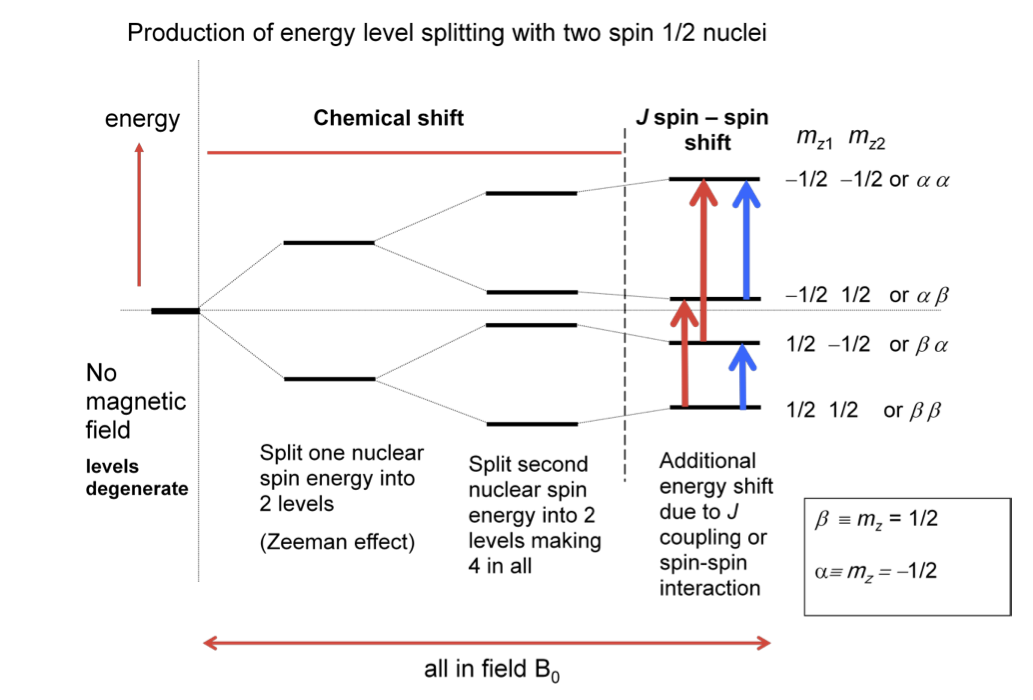
Ahora hay reglas de selección que permiten que la radiación de radiofrecuencia acople diferentes niveles juntos y así producir un espectro. La regla es que el número\(m_z\) cuántico (llamado de diversas maneras número magnético, o acimutal o cuántico de proyección) tiene que cambiar en\(+1\) o\(-1\). Esto significa que en el primer diagrama solo se permiten transiciones los niveles en los que un alfa cambia a beta o viceversa, como lo muestran las flechas verticales. (La regla de selección ocurre porque el fotón (aunque sea a radiofrecuencia) tiene una unidad de momento angular y se conserva el momento angular total).
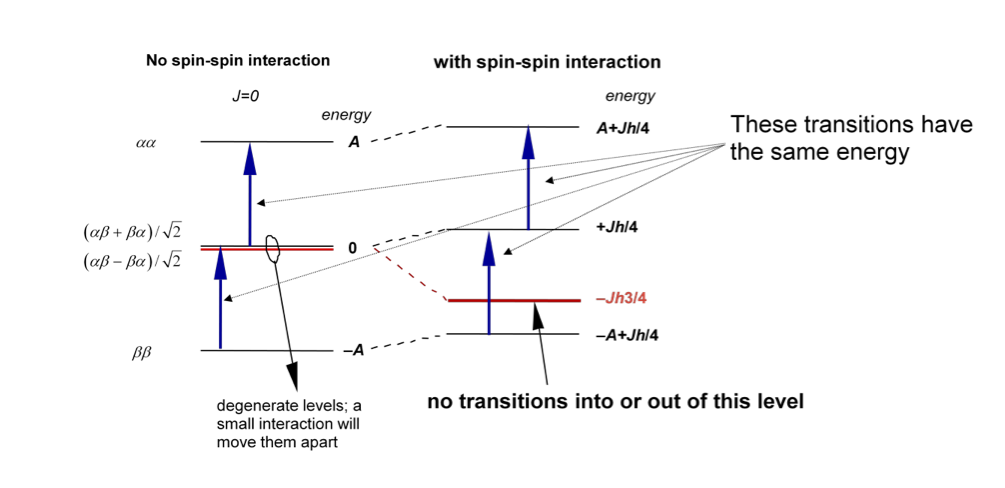
En el caso de núcleos equivalentes (llamado A2) la interacción entre espines todavía está presente pero debido a los núcleos magnéticamente idénticos los estados de espín no son simétricos ni antisimétricos para el intercambio de núcleos y se tiene que hacer una combinación lineal. Esto se muestra a la izquierda de la figura de abajo. La razón por la que no se observa la división en los niveles de energía es que las reglas de selección hacen que las transiciones sean inobservables
Una respuesta alternativa utilizando el formalismo del operador del producto:
La ecuación fundamental que describe mecánicamente la RMN cuántica (descuidando la relajación) es la ecuación de Liouville—von Neumann (en unidades de frecuencia, es decir, ajuste\(\hbar = 1\)):
\[\dfrac{\mathrm d}{\mathrm dt}\hat{\rho}=-\mathrm i[\hat{H},\hat{\rho}] \nonumber \]
Para un sistema de 2 espines con desplazamientos químicos idénticos y un acoplamiento
\[\hat{H}=\Omega\hat{I}_{\!1z}+\Omega\hat{I}_{\!2z}+J(\vec{\hat{I}}_{\!1}\cdot\vec{\hat{I}}_{\!2}) \nonumber \]
Después de un pulso de 90 grados en ambos núcleos la matriz de densidad\(\hat{\rho}\) es de la forma\(\hat{I}_{\!1\chi} + \hat{I}_{\!2\chi}\), donde\(\chi = x\) o\(y\). Ahora es un poco largo pero fácil de demostrar que
\[[\hat{I}_{\!1\chi}+\hat{I}_{\!2\chi},J(\vec{\hat{I}}_{\!1}\cdot\vec{\hat{I}}_{\!2})]=0, \quad \text{with } \chi=x,y,z \nonumber \]
lo que significa que el acoplamiento hamiltoniano no influye en la señal después de un pulso de 90 grados, como\([\hat{H}_\text{coupling},\hat{\rho}] = 0\).
Colaboradores y Atribuciones




