16.2: Ecuaciones de Estado de van der Waals y Redlich-Kwong
- Page ID
- 80035
La ley de gas ideal es válida para bajas presiones, donde el volumen finito de partículas y las atracciones intermoleculares no tienen un gran impacto. A presiones más altas, debemos dar cuenta de estos factores. Las ecuaciones de van der Waals y Redlich-Kwong de estados son ecuaciones de estado que intentan dar cuenta del comportamiento real del gas modificando la ley de gas ideal con dos parámetros adicionales.
La Ecuación de Estado de Van der Waals
La Ecuación de Estado de van der Waals es una ecuación que relaciona la densidad de gases y líquidos con las condiciones de presión, volumen y temperatura (es decir, es una ecuación termodinámica de estado). Se puede ver como un ajuste a la ley de gas ideal que toma en cuenta el volumen distinto de cero de las moléculas de gas y la atracción entre partículas utilizando términos de corrección\(a\) y\(b\). Fue derivado en 1873 por Johannes Diderik van der Waals, quien recibió el Premio Nobel en 1910 por esta obra. La ecuación de estado de van der Waals es:
\[P = \dfrac{nRT}{V - nb} - \dfrac{an^2}{V^2} \label{Eq7} \]
La ecuación también se\(\ref{Eq7}\) puede reescribir como
\[\left(P+{\dfrac {n^{2}a}{V^{2}}}\right)\left(V-nb\right)=nRT \nonumber \]
Si los términos de corrección\(a\) y\(b\) van a cero, la ecuación reduce a la ecuación de gas ideal de estado:
\[PV=nRT \nonumber \]
Primero veamos primero el término de corrección\(b\), que representa los volúmenes de las partículas y asume un potencial de pared dura,\(u_o(r)\). Este término energético potencial describe un sistema de esfera dura “bolas de billar” de diámetro\(\sigma\). La figura 16.2.1 muestra dos de estas partículas tipo bola de billar en el punto de contacto (es decir, la distancia de aproximación más cercana). En este punto, sufren una colisión y se separan, por lo que no pueden estar más cerca que esa distancia.
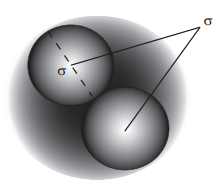
La distancia entre sus centros también lo es\(\sigma\). Debido a esta distancia de aproximación más cercana, el volumen total disponible para las partículas no es el volumen del contenedor\(V\), sino algún volumen menor que\(V\). Esta reducción de volumen se puede calcular. La figura 16.2.1 muestra una esfera sombreada que solo contiene el par de partículas de bola de billar. El volumen de esta esfera es el volumen excluido de dos partículas cualesquiera. El radio de la esfera es\(\sigma\) y el volumen excluido para las dos partículas es\(4 \pi \sigma^3/3\), que es el volumen de la esfera sombreada. A partir de esto, vemos que el volumen excluido para cualquier partícula es apenas la mitad de esta o\(\frac{2}{3} \pi \sigma^3\). El volumen excluido para un mol de tales partículas es el parámetro\(b\):
\[b = \dfrac{2}{3} \pi \sigma^3 N_0 \nonumber \]
Dados los\(n\) moles de gas, el volumen total excluido es entonces\(nb\), de manera que el volumen total disponible es\(V - nb\).
Volvamos nuestra atención al\(a\), que representa los atractivos intermoleculares de las partículas. Las atracciones moleculares tienden a hacer que lo\(P\) ejercido por el gas sea menor que lo predicho por la ley de gas ideal a bajas presiones. \(P\)es la fuerza sobre el área:
\[P=\frac{F}{A} \nonumber \]
La presión es proporcional a la fuerza neta en la pared del contenedor:
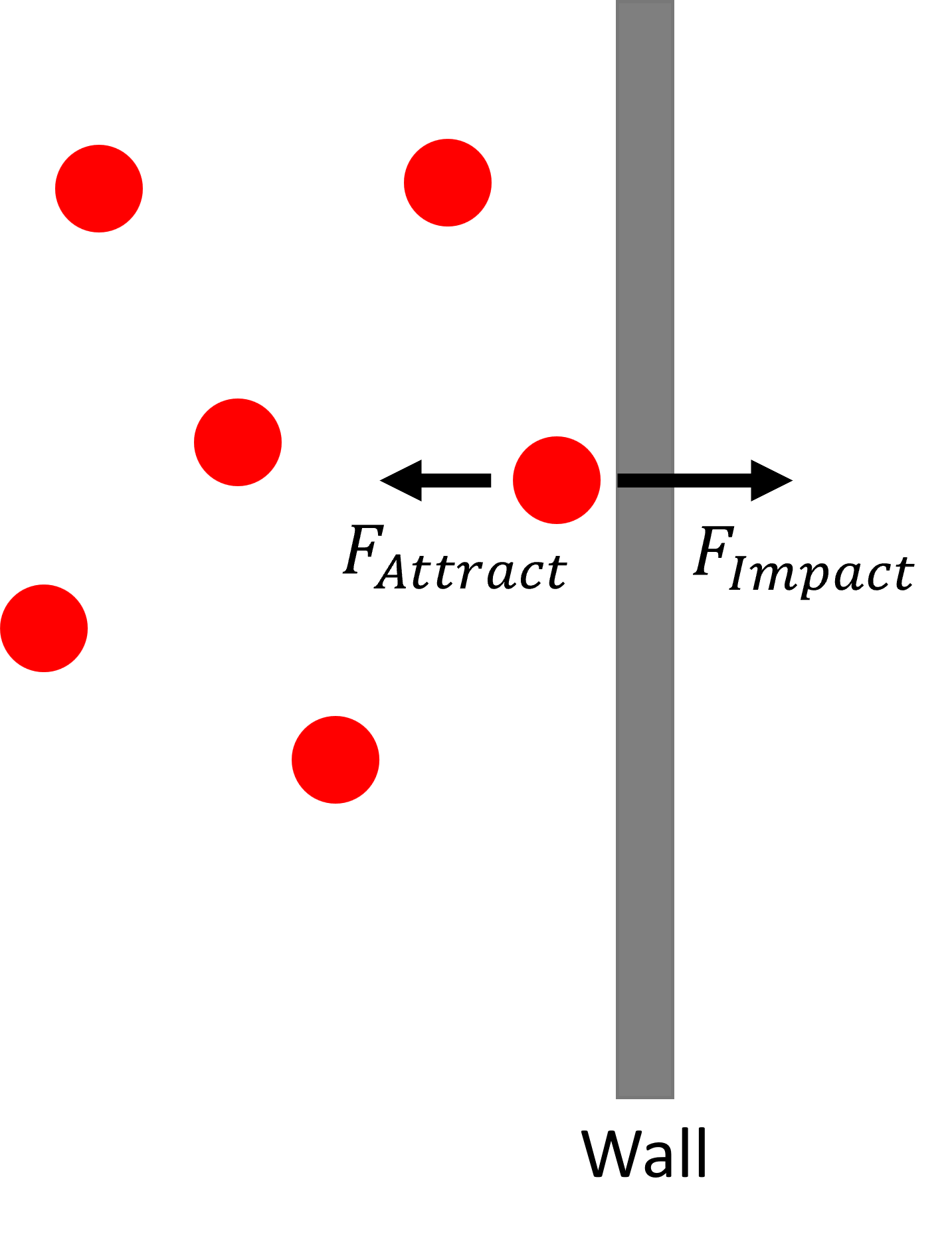
La fuerza neta es la fuerza de las moléculas que impactan la pared del recipiente menos la atracción intermolecular de las moléculas:
\[{\bar{F}}_{Net}={\bar{F}}_{Impact}-{\bar{F}}_{Attract} \nonumber \]
Por lo tanto, la presión será menor para el gas real que para el gas ideal. Podemos agregar un término de corrección a la presión para dar cuenta de las atracciones intermoleculares:
\[P_{VDW}=P_{Real}+a\left(?\right) \nonumber \]
\(V\)influye en la cantidad de atracción intermolecular porque\(P\) se reduce a medida que\(V\) se incrementa:
\[P\propto\frac{1}{V} \nonumber \]
Y la presión es proporcional al número de interacciones atractivas:
# de interacciones moleculares\(\propto P^2\)
# de interacciones moleculares\(\propto \frac{1}{V^2}\)
Ahora tenemos una expresión para los van der Waals\(P\):
\[P=P_{Real}+\frac{an^2}{V^2} \nonumber \]
Las constantes\(a\) y\(b\) dependen de la sustancia. Algunos valores típicos son: 1
| Molécula | \(a\;\sf\left(\frac{L^2\cdot bar}{{mol}^2}\right)\) | \(b\;\sf\left(\frac{L}{mole}\right)\) |
|---|---|---|
| \(\sf H_2O\) | 5.536 | 0.03049 |
| \(\sf N_2\) | 1.43 | 0.03913 |
| \(\sf CH_4\) | 2.283 | 0.04278 |
| \(\sf C_2H_6\) | 5.562 | 0.0638 |
1. R. C. Weast (1972). Manual de Química y Física 53ª Edición. Pub de Caucho Químico.
Ecuación de Estado de Redlich-Kwong
La Ecuación de Estado de van der Waals tuvo que esperar casi 100 años antes de que se le introdujera una mejora real y exitosa. Este avance ocurrió una vez que los investigadores se comprometieron a encontrar la dependencia empírica de la temperatura del parámetro de atracción\(a\) propuesto por van der Waals. En contraste, se ha prestado muy poca atención a modificar el parámetro\(b\) para covolumen. Tiene mucho sentido que\(b\) no se modifique por la temperatura, porque representa el volumen de las moléculas, que no deberían verse afectadas por su energía cinética (medida en términos de temperatura). La primera modificación exitosa notable del parámetro de atracción vino con la publicación de la ecuación de estado de Redlich-Kwong en 1949.
La ecuación de estado de Redlich—Kwong es una ecuación empírica algebraica que relaciona la temperatura, la presión y el volumen de gases. Generalmente es más precisa que la van der Waals y las ecuaciones de estado de gas ideales a temperaturas por encima de la temperatura crítica. Fue formulado por Otto Redlich y Joseph Neng Shun Kwong en 1949, quienes demostraron que una simple ecuación de estado de dos parámetros bien podría reflejar la realidad en muchas situaciones. Redlich y Kwong revisaron la Ecuación de Estado de van der Waals (Ecuación\(\ref{Eq7}\)) y propusieron las siguientes expresiones:
\[ \left( P + \dfrac{a}{\sqrt{T} \bar{V} (\bar{V} + b)} \right) ( \bar{V}-b) = RT \label{10.1} \]
El cambio fundamental que introdujeron fue la forma funcional de\(\partial P_\text{attraction}\). Adicionalmente, introdujeron el covolumen\(b\) en el denominador de esta forma funcional. El concepto importante aquí es que el parámetro\(a\) de atracción de van der Waals necesitaba hacerse una función de la temperatura para hacer un mejor trabajo de igualar cuantitativamente los datos experimentales. Esto era una comprensión que había sugerido van der Waals, pero no se había introducido ninguna dependencia funcional real hasta la ecuación de Redlich-Kwong.
Sabemos lo que sigue en este punto. Para llegar a una expresión para\(a\) y\(b\) de Ecuación\(\ref{10.1}\), aplicamos las condiciones de criticidad a esta ecuación de estado. Como recordamos, imponer las condiciones de criticidad permite relacionar los coeficientes\(a\) y\(b\) con las propiedades críticas (\(P_c\),\(T_c\)) de la sustancia. Una vez hecho eso, obtenemos la definición de\(a\) y\(b\) para la ecuación de estado de Redlich-Kwong:
\[ a =0.42780 \dfrac{R^2T_c^{2.5}}{P_c} \label{10.2a} \]
\[ b =0.086640 \dfrac{RT_c}{P_c} \label{10.2b} \]
La ecuación de estado de Redlich-Kwong mejoró radicalmente, en un sentido cuantitativo, las predicciones de la ecuación de estado de van der Waals. Ahora recordamos que las ecuaciones de tipo van der Waals son cúbicas porque son polinomios cúbicos en volumen molar y factor de compresibilidad. No nos sorprende entonces, que podamos\(\ref{10.1}\) transformar Ecuación en:
\[ \bar{v} ^3 - \left( \dfrac{RT}{P} \right)\bar{v}^2 + \dfrac{1}{P} \left( \dfrac{1}{T^{0.5}} - bRT - Pb^2 \right) \bar{v} - \dfrac{ab}{PT^{0.5}} = 0 \label{10.3} \]
y, definiendo los siguientes parámetros:
\[ A = \dfrac{aP}{R^2T^{2.5}} \label{10.3a} \]
\[ B =\dfrac{bP}{RT} \label{10.3b} \]
e introduciendo la definición del factor de compresibilidad:
\[Z = \dfrac{P\bar{v}}{RT} \nonumber \]
obtenemos:
\[ Z^3 -Z^2 + (A -B -B^2) Z -AB =0 \label{10.4} \]
También podemos verificar la teoría de estado correspondiente de dos parámetros introduciendo Ecuaciones\(\ref{10.2a}\),\(\ref{10.2b}\), y\(\ref{10.3}\) en Ecuación\(\ref{10.4}\):
\[Z^3−Z^2+\dfrac{P_r}{T_r} \left( \dfrac{0.42748}{T_r^{1.5}} −0.08664−0.007506 \dfrac{P_r}{T_r} \right)Z−0.03704 \dfrac{P^2_r}{T^{3.5}_r}=0 \label{10.5} \]
Donde:
\[P_r=\frac{P}{P_c} \nonumber \]
\[T_r=\frac{T}{T_c} \nonumber \]
\(P_r\)y\(T_r\) son la presión y la temperatura en el estado reducido. Consulte la Sección 16.4 para obtener más información sobre estados reducidos. En Ecuación\(\ref{10.5}\), podemos observar lo mismo que vimos con la ecuación de estado de van der Waals: los gases en los estados correspondientes tienen las mismas propiedades. Ecuación\(\ref{10.5}\) es particularmente clara al respecto: cualesquiera dos gases diferentes a la vez\(P_r\),\(T_r\) condición tienen el mismo factor de compresibilidad.
Así como cualquier otra ecuación cúbica de estado, las ecuaciones\(\ref{10.1}\) a través de\(\ref{10.5}\), tal como están, deben aplicarse a sustancias puras. Para mezclas, sin embargo, aplicamos la misma ecuación, pero imponemos ciertas reglas de mezcla para obtener\(a\) y\(b\), que son funciones de las propiedades de los componentes puros. Estrictamente hablando, creamos una nueva sustancia “pseudo” pura que tiene las propiedades promedio de la mezcla. Redlich-Kwong conservó las mismas reglas de mezcla que van der Waals propuso para su ecuación de estado:
\[ a_m = \sum_i \sum_j y_iy_j a_{ij} \nonumber \]
con
\[a_{ij} = \sqrt{a_ia_j} \nonumber \]
y
\[ b_{m}=\sum_i y_ib_i \nonumber \]
Naturalmente, Redlich y Kwong no tuvieron la última palabra sobre posibles mejoras a la ecuación de estado de van der Waals. La ecuación de estado de Redlich-Kwong, como se muestra aquí, ya no se usa en aplicaciones prácticas. La investigación continuó y trajo consigo nuevos intentos de mejorar la ecuación de estado de Redlich-Kwong. Después de más de dos décadas, se desarrolló una ecuación de estado de Redlich-Kwong modificada con muy buen potencial.
Colaboradores y Atribuciones
Michael Adewumi (The Pennsylvania State University) Vice Provost for Global Program, Professor of Petroleum and Natural Gas Engineering
- Template:ContribLaRue

