16.3: Una ecuación cúbica de estado

Isotermas

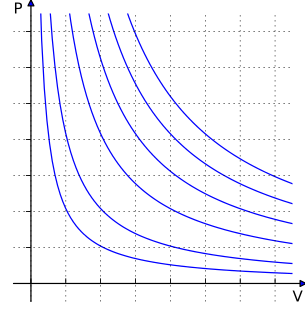
Las isotermas son gráficas de la presión de un gas en función del volumen a una temperatura constante fija. Las isotermas para un gas ideal son las hipberbolas:

\[P=\dfrac{RT}{\bar{V}} \nonumber \]

donde\(\bar{V}\) está el volumen molar\(V/n\). Sabemos que a temperaturas suficientemente bajas, cualquier gas real, cuando se comprime, debe sufrir una transición de gas a líquido. La firma de tal transición es un cambio discontinuo en el volumen, lo que significa la condensación del gas en un líquido que ocupa un volumen significativamente menor.

Figura 16.3.1 : Isotermas de gas ideales para un mol del gas y a temperaturas seleccionadas. (dominio público).

Las isotermas de CO ₂ para la Ecuación de estado de van der Waals se muestran en la Figura 16.3.2 . A temperaturas suficientemente altas, las isotermas se acercan a las de un gas ideal. A temperaturas más bajas, el fluido obedece aproximadamente a la ley de gas ideal\(PV=nRT\) a grandes volúmenes cuando las presiones son bajas. Si disminuimos el volumen (vamos a la izquierda en la figura a lo largo de una isoterma), la presión sube. Considera la isoterma (azul) de 10 °C, que está por debajo de la temperatura crítica. Disminuir el volumen hasta llegar al punto\(B\), donde comienza la condensación (formación de CO ₂ líquido). En este punto la curva de van der Waals ya no es física (excluyendo la posibilidad de la ocurrencia de un gas sobresaturado, metaestable) porque\(P\) y\(V\) aumentan juntos. Debe quedar claro que muchas aproximaciones y supuestos entran en la derivación de la ecuación de van der Waals para que falte en el modelo parte de la física importante. De ahí que no nos sorprenda si la ecuación de van der Waals tiene algún comportamiento antifísico enterrado en ella. En realidad, la presión se mantiene constante entre la región\(A\)\(B\) y y el comportamiento físico real viene dado por la línea azul discontinua, llamada línea de empate. Estas líneas representan la coexistencia gas-líquido y la presión es igual a la presión de vapor del líquido.

Figura 16.3.2 : Diferentes isotermas (curvas de temperatura constante) de la ecuación de estado de van der Waals usando parámetros\(a\) y\(b\) calculadas para dióxido de carbono. La línea discontinua de A a B se dibuja de acuerdo con la regla de área igual de Maxwell. La molécula de dióxido de carbono (CO ₂) tiene p _C = 7.37 MPa y T _C = 304.1 K = 31 ˚C, lo que da a = 0.366 m ⁶ Pa y b = 42.9 10 ^-6 m ³. La presión crítica es de 73.7 bar = 7370 kPa.

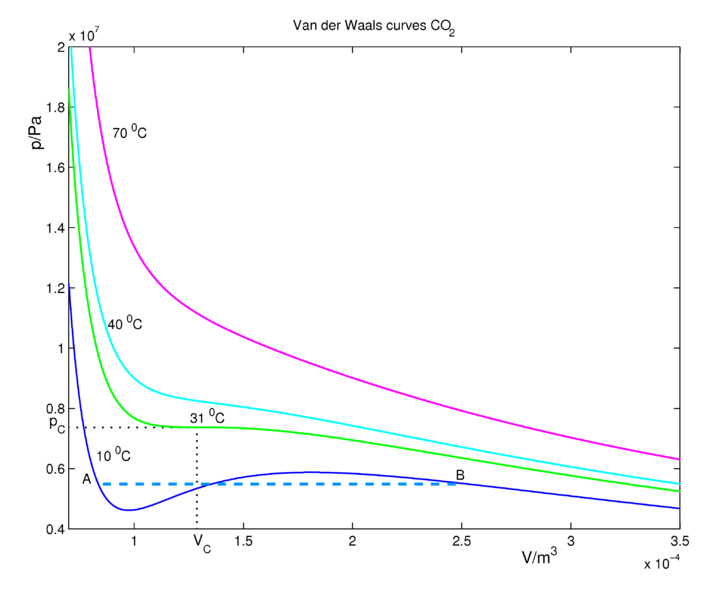
La línea de unión se debe agregar en ad hoc dibujando una línea horizontal a través de la isoterma (Figura 16.3.2 ). La posición vertical de la línea se elige para que el área por encima de la línea (entre la línea y la isoterma) y por debajo de la línea (nuevamente entre la línea y la isoterma) sea exactamente la misma. Esto se conoce como la construcción de Maxwell. De esta manera, eliminamos por completo el artefacto del incremento no físico de\(P\) con\(V\) cuando calculamos el trabajo de compresión sobre el gas de\(\int P(V) \: dV\), para ser discutido en nuestra sección sobre termodinámica. Si bien las curvas de van der Waals tienen regiones donde no son físicas, la ecuación para estas curvas, derivada por van der Waals en 1873, fue un gran logro científico.

Nota

Aún hoy en día no es posible dar una sola ecuación que describa correctamente la transición de fase gas-líquido.

Punto crítico

Mirando a la izquierda del punto\(A\) sobre la isoterma de 10 °C (curva azul), el sistema se encuentra en estado líquido. Aumentar el volumen a punto\(A\) conduce a una rápida caída en la presión del sistema debido a que la compresibilidad de un líquido es considerablemente menor que la de un gas. El sistema todavía se encuentra en estado líquido en el punto\(A\), pero a medida que aumentamos el volumen más, ingresamos a la línea de coexistencia gas-líquido y el líquido comienza a pasar a gas. A medida que avanzamos por esta línea hacia la derecha, hay menos líquido y más gas en el sistema hasta llegar al punto\(B\), momento en el que el sistema estará completamente en fase gaseosa. Las áreas, delimitadas por la isoterma de 10 °C (curva azul) por debajo y por encima de la línea de coexistencia son iguales. Cualquier aumento adicional en el volumen conducirá a una expansión del gas.Hay exactamente una isoterma a lo largo de la cual la ecuación de van der Waals predice correctamente la transición de fase gas a líquido. Si se sigue la isoterma de 31 °C (curva verde en la Figura 16.3.2 ) de temperatura crítica, la discontinuidad de volumen capturada por la línea de enlace se reduce a un solo punto (para que no haya posibilidad de un aumento de\(P\) con\(V\)!). Este punto se llama punto crítico y existe a una sola temperatura, llamada temperatura crítica, denotada\(T_c\). La isoterma crítica a la temperatura crítica corresponde a la temperatura más alta posible a la que puede ocurrir una transición gas-líquido. Las isotermas a temperaturas más altas no tienen transiciones de fase líquido-gas. A lo largo de esas isotermas, el fluido de mayor presión, llamado fluido supercrítico, se asemeja a un líquido, mientras que a presiones más bajas el fluido es más parecido al gas.

El punto crítico existe en una inflexión donde la primera y segunda derivadas de\(P\) con respecto a\(V\) son cero:

\[\left(\frac{\partial P}{\partial V}\right)_{T_c} = 0 \nonumber \]

\[\left(\frac{\partial^2 P}{\partial V^2}\right)_{T_c} = 0 \nonumber \]

Sustituyendo la ecuación de van der Waals en estas dos condiciones, encontramos lo siguiente:

\[\begin{align} -\dfrac{nRT_c}{\left( V_c - nb \right)^2} + \dfrac{2 an^2}{V_c^3} &= 0 \\ \dfrac{2nRT_c}{\left(V_c - nb \right)^3} - \dfrac{6an^2}{V_c^4} &= 0 \end{align} \label{{{template.Index(ID:1)}}0} \]

De ahí que tengamos dos ecuaciones en dos incógnitas\(V_c\) y\(T_c\) para la temperatura crítica y el volumen crítico. Una vez determinados estos, la ecuación de van der Waals, en sí misma, nos permite determinar la presión crítica,\(P_c\). Para resolver las ecuaciones, primero divide una por otra. Esto nos da una condición simple para el volumen:

\[\begin{align} \dfrac{V_c - nb}{2} &= \dfrac{V_c}{3} \\ 3V_c - 3nb &= 2V_c \\ V_c &= 3nb \end{align} \label{{{template.Index(ID:1)}}1} \]

Este es el volumen crítico. Ahora use cualquiera de las dos condiciones para obtener la temperatura crítica,\(T_c\). Si usamos el primero, encontramos:

\[\begin{align} \dfrac{nRT_c}{\left( V_c - nb \right)^2} &= \dfrac{2an^2}{V_c^3} \\ \dfrac{nRT_c}{\left( 3nb - nb \right)^2} &= \dfrac{2an^2}{\left( 3nb \right)^3} \\ \dfrac{nRT_c}{4n^2b^2} &= \dfrac{2an^2}{27n^3b^3} \\ RT_c &= \dfrac{8a}{27b} \end{align} \label{{{template.Index(ID:1)}}2} \]

Finalmente, tapando la temperatura crítica y el volumen en la ecuación de van der Waals, obtenemos la presión crítica:

\[\begin{align} P_c &= \dfrac{nRT_c}{V_c - nb} - \dfrac{an^2}{V_c^2} \\ &= \dfrac{8an/27b}{3nb - nb} - \dfrac{an^2}{\left( 3nb \right)^2} \\ &= \dfrac{a}{27b^2} \end{align} \label{{{template.Index(ID:1)}}3} \]

No sorprende que las ecuaciones cúbicas de estado como las ecuaciones de estado de van der Waals (y Redlich-Kwong) produzcan tres raíces diferentes para el volumen y el factor de compresibilidad. Esto es simplemente porque son ecuaciones algebraicas, y cualquier ecuación algebraica de orden n siempre dará “n” raíces. Sin embargo, esas “n” raíces no están obligadas a ser distintas, y eso no es todo: tampoco se requiere que sean números reales. Una expresión cuadrática (n = 2) puede tener cero raíces reales (e.g.,\(x^2 + 1 = 0\)); esto se debe a que esas raíces son números complejos. En el caso de las expresiones cúbicas (n = 3), tendremos una o tres raíces reales; esto se debe a que las raíces complejas siempre aparecen en parejas (es decir, una vez que se tiene una raíz compleja, su conjugado también debe ser una solución). En nuestro caso, y debido a que estamos tratando con cantidades físicas (densidades, volúmenes, factores de compresibilidad), solo son de interés las raíces reales. Más específicamente, buscamos raíces reales, positivas tales que\(\bar{V} > b\) en el caso del volumen molar y\( Z > \frac{Pb}{RT}\) en el caso del factor de compresibilidad.

En una ecuación cúbica de estado, la posibilidad de tres raíces reales se restringe al caso de condiciones subcríticas (\(T < T_c\)), debido a que el comportamiento en forma de S, que representa la transición vapor-líquido, se produce solo a temperaturas por debajo de las críticas. Esta restricción es impuesta matemáticamente por las condiciones de criticidad. En cualquier otro lugar, más allá de la curva en forma de S, solo obtendremos una raíz real del tipo\(\bar{V} > b\). La figura 16.3.3 ilustra este punto.

Figura 16.3.3 : Múltiples raíces en EOS Cúbicos

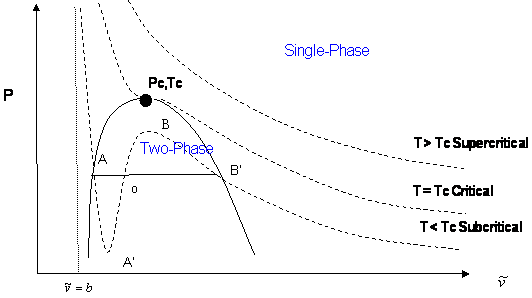
La forma de la isoterma crítica en el punto crítico nos permite determinar la temperatura, presión y volumen exactos a los que ocurrirán las transiciones de fase de gas a líquido. Si trazamos una curva a través de las isotermas uniendo todos los puntos de estas isotermas en los que comienzan las líneas de enlace, continuamos la curva hasta la isoterma crítica, y bajando por el otro lado donde terminan las líneas de enlace, esta curva alcanza un máximo en el punto crítico. La región dentro de esta curva es cuando coexisten las fases gas y líquida.

Resumimos los tres casos presentados en la Figura 16.3.3 :

1. Isotermas supercríticas (\(T > T_c\): A temperaturas más allá de las críticas, la ecuación cúbica tendrá solo una raíz real (las otras dos son conjugados complejos imaginarios). En este caso, no hay ambigüedad en la asignación de la raíz de volumen ya que tenemos condiciones monofásicas. La ocurrencia de una raíz real única sigue siendo válida a cualquier presión: cualquier línea horizontal (isobárica) corta la isoterma supercrítica solo una vez en la Figura 16.3.3 .
2. Isoterma crítica (\(T = T_c\)): En el punto crítico (\(P = P_c\)), las propiedades de vapor y líquido son las mismas. En consecuencia, la ecuación cúbica predice tres raíces reales e iguales en este punto especial y particular. Sin embargo, para cualquier otra presión a lo largo de la isoterma crítica (\(P < P_c\)o\(P > P_c\),) la ecuación cúbica da una raíz real única con dos conjugados complejos.
3. Isoterma subcrítica (\(T < T_c\)): Las predicciones para presiones dentro del rango de presión para la metaestabilidad (\(P_A’ < P < P_B’\)) o para la condición de saturación (\(P = P^{sat}\)) siempre producirán tres raíces reales y diferentes. De hecho, esta es la única región donde una isobarra corta la misma isoterma más de una vez. La raíz más pequeña se toma como el volumen específico de la fase líquida; la mayor es el volumen específico de la fase de vapor; la raíz intermedia no se calcula ya que carece de sentido físico. No obstante, no se deje llevar. Las condiciones subcríticas no siempre darán tres raíces reales del tipo\(\bar{\nu} > b\). Si la presión es superior al máximo de la curva en forma de S\(P_B\), solo tendremos una raíz real (líquida) que satisfaga\(\bar{\nu} > b\). De la misma manera, las presiones entre\(0 < P < P_A’\) producen solo una raíz (vapor). En el caso de\(P_A’\) ser un número negativo, se encuentran tres raíces reales incluso para presiones muy bajas cuando se aplica la ley de gas ideal. La raíz más grande es siempre la elección correcta para el volumen molar en fase gaseosa de los componentes puros.

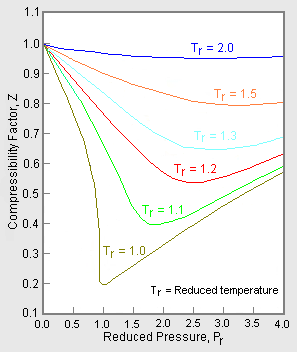
La mayoría de estas consideraciones se aplican a la ecuación cúbica de estado en\(Z\) (factor de compresibilidad). La representación gráfica más común del factor de compresibilidad es la conocida gráfica de Standing y Katz, donde la compresibilidad\(Z\),, se grafica contra la presión (Figura 16.3.4 ). Standing y Katz presentaron su tabla para el factor de compresibilidad de los gases naturales dulces en 1942. Este gráfico se basó en datos experimentales. La determinación gráfica de las propiedades estuvo muy extendida hasta el advenimiento de las computadoras, y así el gráfico Z de Standing y Katz se hizo muy popular en la industria del gas natural. Los gráficos típicos de pie y Katz se dan para condiciones de alta temperatura (\(T > T_c\)o\(T_r > 1\)).

Figura 16.3.4 : Factor de compresibilidad versus presión

Colaboradores y Atribuciones

•  Michael Adewumi (The Pennsylvania State University) Vice Provost for Global Program, Professor of Petroleum and Natural Gas Engineering

• Template:ContribLaRue
• Citizendium