17.4: La capacidad calorífica a volumen constante es el cambio en la energía interna con la temperatura

La capacidad calorífica a volumen constante (\(C_V\)) se define como el cambio en la energía interna con respecto a la temperatura:

\[C_V = \left( \dfrac{\partial U}{\partial T} \right)_{N, V} \label{Eq3.26} \]

Desde:

\[E = -\dfrac{\partial \ln{Q(N, V, \beta)}}{\partial \beta} \label{Eq3.27} \]

Vemos que:

\[\begin{align} C_V &= \dfrac{\partial U}{\partial T} \nonumber \\[4pt] &= \dfrac{\partial U}{\partial \beta} \dfrac{\partial \beta}{\partial T}  \nonumber \\[4pt] &= \dfrac{1}{kT^2} \dfrac{\partial^2}{\partial \beta^2} \: \ln Q(N, V, \beta) \nonumber\\[4pt] &= k \beta^2 \dfrac{\partial^2}{\partial \beta^2} \: \ln Q(N, V, \beta) \label{Eq3.28} \end{align} \]

donde\(k\) está la constante de Boltzmann. La energía se puede almacenar en materiales/gases a través de poblar los grados específicos de libertad que existen en la muestra. Comprender cómo ocurre esto requiere el uso de Mecánica Cuántica.

Dulong-Petit Ley sobre las Capacidades Térmicos de Sólidos

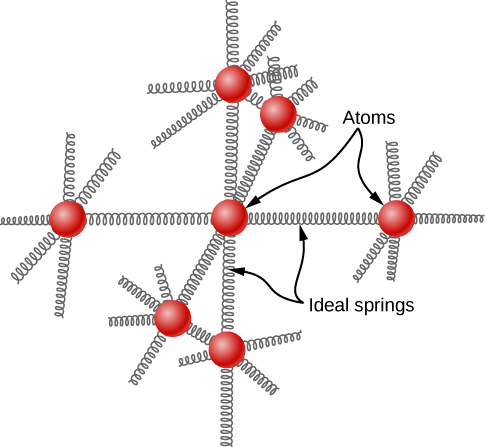
Pierre Louis Dulong y Alexis Thèrèse Petit realizaron experimentos en 1819 en cristales sólidos tridimensionales para determinar las capacidades térmicas de una variedad de estos sólidos (la capacidad calorífica es la capacidad de los sólidos para absorber y retener calor). Dulong y Petit descubrieron que todos los sólidos investigados tenían una capacidad calorífica de aproximadamente 2.49 x 10 ⁴ J kilomol ^{-1 -1} a alrededor de 298 K o temperatura ambiente. El resultado de su experimento se explicó considerando cada átomo dentro del sólido como un oscilador con seis grados de libertad (un oscilador puede pensarse como un resorte que conecta todos los átomos en la red sólida). Estos resortes se extienden hacia el espacio tridimensional. Cuanta más energía se le agrega al sólido, más vibran estos resortes. Cada átomo tiene una energía de\(\frac{1}{2}kT\), donde\(k\) está la constante de Boltzmann y\(T\) es la temperatura absoluta. Por lo tanto,

\[ C_V=\dfrac{6R}{2}=3R \label{1}\tag{Dulong-Petit Law} \]

El número 6 en esta ecuación es el número de grados de libertad para la molécula. Petit y Dulong sugirieron que estos resultados apoyaron su base para la capacidad calorífica de los sólidos. La explicación para el experimento de Petit y Dulong no fue suficiente cuando se descubrió que la capacidad calorífica disminuyó a medida que la temperatura se acercaba al cero absoluto. Los grados de libertad no disminuyen la velocidad ni dejan de moverse cuando el sólido alcanza una temperatura suficientemente fría. Se propuso un modelo adicional para explicar esta desviación. Se desarrollaron dos teorías principales para explicar esta desconcertante desviación en los experimentos de capacidad calorífica. El primero fue construido por Einstein y el segundo fue escrito por Debye.

Figura 17.4.1 : En un modelo simple de un elemento sólido, cada átomo está unido a otros por seis resortes, dos por cada movimiento posible: x, y y z. Cada uno de los tres movimientos corresponde a dos grados de libertad, uno para energía cinética y otro para energía potencial. (CC BY-SA 4.0; OpenStax).

Teoría de Einstein sobre las capacidades térmicas de los sólidos

Einstein asumió tres cosas cuando investigó la capacidad calorífica de los sólidos. En primer lugar, asumió que cada sólido estaba compuesto por una estructura reticular constituida por\(N\) átomos. Cada átomo fue tratado como moviéndose independientemente en tres dimensiones dentro de la red (3 grados de libertad). Esto significó que todo el movimiento vibratorio de la celosía podría describirse mediante un total de\(3N\) movimientos, o grados de libertad. En segundo lugar, asumió que los átomos dentro de la red sólida no interactuaban entre sí y en tercer lugar, todos los átomos dentro del sólido vibraban a la misma frecuencia. El tercer punto destaca la principal diferencia en los dos modelos de Einstein y Debye.

El primer punto de Einstein es exacto porque los datos experimentales apoyaron su hipótesis, sin embargo su segundo punto no es porque si los átomos dentro de un sólido no pudieran interactuar, el sonido no podría propagarse a través de él. Por ejemplo, los átomos de un diapasón, cuando son golpeados, interactúan entre sí para crear un sonido que viaja a través del aire hasta el oído del oyente. Los átomos también interactúan en un sólido cuando se calientan. Toma por ejemplo una sartén. Si la sartén se calienta por un lado, el calor se transfiere por todo el metal calentando efectivamente toda la sartén. Las moléculas que componen la sartén interactúan para transferir calor. De la misma manera los osciladores en un sólido interactúan cuando se agrega energía al sistema. La extensión de estas interacciones conduce a la capacidad calorífica observada físicamente.

La capacidad calorífica de un sólido a un volumen constante es

\[ \begin{align*} C_V &= \left(\dfrac{\partial{U}}{\partial{T}}\right)_V \\[4pt] &=3Nk\left(\dfrac{\theta_E}{T}\right)^2 \label{2} \\[4pt] &= \dfrac{\exp \left(\dfrac{\theta_E}{T} \right)}{\left(\exp \dfrac{\theta_E}{T} -1\right)^2} \end{align*} \]

donde

• \(\theta_E=\dfrac{hv}{k}\)es la temperatura de Einstein,
• \(h\)es la constante de Planck,
• \(k\)es la constante de Boltzmann, y
• \(\nu\)es la frecuencia del oscilador de los átomos dentro del sólido.

La accesibilidad de la temperatura de Einstein de la energía vibratoria dentro de una molécula sólida determina la capacidad calorífica de ese sólido. Cuanto mayor sea la accesibilidad, mayor será la capacidad calorífica. Si la energía vibratoria es fácilmente accesible las colisiones en la molécula tienen una mayor probabilidad de excitar el átomo a un nivel vibracional superior. Esto se muestra a continuación.

Figura 17.4.2 : Esta figura ilustra el efecto de la temperatura de Einstein sobre la probabilidad de que un oscilador absorba energía de una colisión y transfiera esa energía al calor almacenado o a la capacidad calorífica. A medida que aumenta la temperatura de Einstein, mayor es la probabilidad de que un oscilador esté excitado al siguiente estado vibracional. (CC BY-NC 4.0; Ümit Kaya vía LibreTexts)

Entonces la temperatura de Einstein indica específicamente la probabilidad que una molécula tiene en sus grados de libertad para almacenar energía en sus osciladores (o enlaces) atómicos. La comparación de la temperatura de Einstein con los valores clásicos tradicionales de capacidad calorífica ilustrará las diferencias entre las resistencias específicas (alta temperatura) y las debilidades (baja temperatura) del modelo de Einstein.

Figura 17.4.3 :Esta gráfica muestra la precisión de la temperatura de Einstein a bajas temperaturas. El modelo clásico es efectivo a temperaturas superiores a 10 Temperaturas de Einstein. (Cc BY-NC; Ümit Kaya vía LibreTexts)

Así, en el límite de temperatura alta (\(\dfrac{\theta_E}{T}\ll 1\)) (es decir, la temperatura es muy grande en comparación con la temperatura de Einstein) entonces

\[ C_V \approx 3Nk=3nR. \label{4} \]

El modelo de Einstein revela la precisión del modelo Petit y Dulong y modela las altas temperaturas con precisión. Sin embargo, así como el modelo de Petit y Dulong disminuyó en precisión a medida que disminuía la temperatura, así siguió el de Einstein.

Al examinar el límite de temperatura extremadamente bajo:\(\dfrac{\theta_E}{T}\gg1\), se puede ver:

\[ C_V=3Nk\left(\dfrac{\theta_E}{T}\right)^2e^\dfrac{-\theta_E}{T} \label{5} \]

A medida que la temperatura (\(T\)) va a cero, la porción exponencial de la ecuación anterior va a cero y por lo tanto\(C_V\) también se acerca a cero. Esto apoya los valores experimentales a medida que la temperatura se acerca a cero, la capacidad calorífica del sólido también disminuye a cero.

La teoría de Einstein también explica sólidos que exhiben una baja capacidad calorífica incluso a temperaturas relativamente altas. Un ejemplo de tal sólido es el diamante. La capacidad calorífica del diamante se acerca a\(3Nk\) medida que la temperatura aumenta considerablemente. El modelo de Einstein apoya esto a través de la definición de una temperatura de Einstein. A medida que aumenta la temperatura de Einstein,\(\nu\) debe aumentar de igual manera. Esto es el equivalente a que cada átomo posee más energía y por lo tanto vibra más rápidamente dentro del propio sólido. La frecuencia del oscilador,\(\nu\), se puede escribir como:

\[ \nu=\dfrac{1}{2\pi}\sqrt{\dfrac{\kappa}{\mu}} \label{6} \]

donde\(\kappa\) es la constante de fuerza y\(\mu\) es la masa reducida. Esta fórmula predice mejor sólidos con constantes de fuerza altas o masas reducidas bajas. Esto corrige desviaciones del modelo Petit y Dulong.

Figura 17.4.4 . Esta gráfica indica la capacidad calorífica de varios metales sólidos en función de la temperatura de Einstein:\(\theta_E=\dfrac{hv}{k_B}\).

Esencialmente, la temperatura de Einstein permite que la ecuación de capacidad calorífica y las frecuencias vibracionales en el sólido cambien a medida que cambia la temperatura. Esto se ajusta efectivamente a las desviaciones observadas en el modelo Petit/Dulong. A medida que la temperatura aumenta o disminuye, la temperatura de Einstein aumenta o disminuye de igual manera para reflejar la actividad física real dentro del sólido.

Figura 17.4.5 . Esta gráfica muestra la capacidad calorífica del plomo en comparación con los valores esperados calculados a partir del modelo de Einstein.

El modelo de Einstein predice bien temperaturas relativamente bajas. Sin embargo, al disminuir desde aproximadamente 15 K, el modelo de Einstein se desvía de los valores experimentales. También, esto se puede observar, aunque no tan dramáticamente, para temperaturas de 25 K a 30 K. Claramente aún falta un término o corrección en el modelo de Einstein para aumentar su precisión.