17.5: La presión se puede expresar en términos de la función de partición canónica
- Page ID
- 79615
La presión también se puede derivar de la función de partición canónica. La presión promedio es la suma de la probabilidad por la presión:
\[ \langle P \rangle = \sum_i{P_i(N,V,T)P_i(N,V)} \nonumber \]
La presión de un sistema macroscópico es:
\[ P(N,V) = -\left(\dfrac{\partial E_i}{\partial V}\right)_N \nonumber \]
Entonces podemos escribir la presión promedio como:
\[\begin{split} \langle P \rangle &= \sum_i{P_i(N,V,\beta)\left(-\dfrac{\partial E_i}{\partial V}\right)_N} \\ &= \sum_i{\left(-\dfrac{\partial E_i}{\partial V}\right)_N\dfrac{e^{-E_i(N,V)/kT}}{Q(N,V,T)}} \end{split} \nonumber \]
En unos pocos pasos podemos mostrar que la temperatura se puede expresar en términos de la función de partición:
\[ Q(N,V,T) = \sum_i{e^{-E_i(N,V)/kT}} \nonumber \]
Escribiendo en términos de temperatura\(\beta\) en lugar de:
\[ Q(N,V,\beta) = \sum_i{e^{-\beta E_i(N,V)}} \nonumber \]
La derivada de la función de partición con respecto al volumen es:
\[ \left(\dfrac{\partial Q}{\partial V}\right)_{N,\beta} = -\beta \sum_i{\left(\dfrac{\partial E_i}{\partial V}\right)_{N}e^{-\beta E_i(N,V)}} \nonumber \]
La presión promedio se puede escribir como:
\[ \langle P \rangle = \dfrac{kT}{Q(N,V,\beta}\left(\dfrac{\partial Q}{\partial V}\right)_{N,\beta} \nonumber \]
Lo que demuestra que la presión se puede expresar únicamente en términos de la función de partición:
\[ \langle P \rangle = kT\left(\dfrac{\partial \ln{Q}}{\partial V}\right)_{N,\beta} \nonumber \]
Podemos usar este resultado para derivar la ley de gas ideal. Para\(N\) partículas de un gas ideal:
\[ Q(N,V,\beta) = \dfrac{[q(V,\beta)]^N}{N!} \nonumber \]
donde:
\[ q(V,\beta) = \left(\dfrac{2\pi m}{h^2\beta}\right)^{3/2}V \nonumber \]
es la función de partición traslacional. La utilidad de expresar la presión como logaritmo queda clara a partir del hecho de que podemos escribir:
\[\begin{split} \ln{Q} &= N\ln{q}-\ln{N!} \\ &= -\dfrac{3N}{2}\ln{\left(\dfrac{2\pi m}{h^2\beta}\right)}+N\ln{V}-\ln{N!} \end{split} \nonumber \]
Hemos utilizado la propiedad de logaritmos que\(\ln{(AB)} = \ln{(A)} + \ln{(B)}\) y\(\ln{(X^Y)} = Y\ln{(X)}\). Sólo un término en el ln\(Q\) depende de\(V\). Tomando la derivada de\(N\ln{V}\) con respecto a\(V\) da:
\[ \left(\dfrac{\partial \ln{Q}}{\partial V}\right)_{N,\beta} = \dfrac{N}{V} \nonumber \]
Sustituyendo esto en la ecuación anterior para la presión da:
\[ P = \dfrac{NkT}{V} \nonumber \]
que es la ley de gas ideal. Recordemos que\(Nk = nR\) donde\(N\) está el número de moléculas y\(n\) está el número de moles. \(R\)es la constante universal del gas (8.314 J/mol-k) que no es más que\(k\) multiplicada por el número de Avagadro. \(N_Ak = R\)convierte la constante de una base “por molécula” a “por mol”.
Gas Comprimido por un Pistón
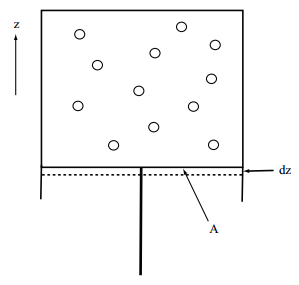
Consideremos un experimento de pensamiento simple, que se ilustra en la figura anterior: Un sistema de\(N\) partículas es comprimido por un pistón que empuja en la\(z\) dirección positiva. Dado que se trata de un experimento de pensamiento clásico, pensamos en términos de fuerzas. El pistón ejerce una fuerza constante de magnitud\(F\) sobre el sistema. La dirección de la fuerza es puramente en la\(z\) dirección positiva, para que podamos escribir el vector de fuerza\(\bf{F}\) como\(\bf{F} = \begin{pmatrix} 0, 0, F \end{pmatrix}\). En equilibrio (el pistón no se mueve), el sistema ejerce una fuerza igual y opuesta sobre el pistón de la forma\(\begin{pmatrix} 0, 0, -F \end{pmatrix}\). Si la energía del sistema es\(E\), entonces la fuerza ejercida por el sistema sobre el pistón vendrá dada por el cambio negativo\(E\) con respecto a\(z\):
\[-F = -\dfrac{dE}{dz} \label{Eq3.29} \]
o:
\[F = \dfrac{dE}{dz} \label{Eq3.30} \]
La fuerza ejercida por el sistema sobre el pistón se manifiesta como una presión observable\(P\) igual a la fuerza\(F\) dividida por el área\(A\) del pistón,\(P=F/A\). Ante esto, la presión observada es justa:
\[P = \dfrac{dE}{Adz} \label{Eq3.31} \]
Ya que el volumen disminuye cuando se comprime el sistema, lo vemos\(Adz = -dV\). De ahí que podamos escribir la presión como\(P = -dE/dV\).
Por supuesto, la relación\(P = -dE/dV\) es termodinámica, pero necesitamos una función de la\(x\) que podamos promediar sobre el conjunto. La elección más natural es:
\[p(x) = -\dfrac{d \mathcal{E} (x)}{dV} \label{Eq3.32} \]
para que\(P = \langle p(x) \rangle\). Al establecer el promedio, obtenemos:
\[\begin{align} P &= -\dfrac{C_N}{Q(N, V, T)} \int \dfrac{\partial \mathcal{E}}{\partial V} e^{-\beta \mathcal{E} (x)} \\ &= \dfrac{C_N}{Q(N, V, T)} \dfrac{1}{\beta} \int \dfrac{\partial}{\partial V} e^{-\beta \mathcal{E} (x)} \\ &= \dfrac{kT}{Q(N, V, T} \dfrac{\partial}{\partial V} C_N \int e^{-\beta \mathcal{E} (x)} \\ &= kT \left( \dfrac{\partial \: \text{ln} \: Q(N, V, T)}{\partial V} \right) \end{align} \label{Eq3.33} \]
Gas Ideal en el Conjunto Canónico
Recordemos que la energía mecánica para un gas ideal es:
\[\mathcal{E} (x) = \sum_{i=1}^N \dfrac{\textbf{p}_i^2}{2m} \label{Eq3.36} \]
donde todas las partículas son idénticas y tienen masa\(m\). Así, la expresión para la función de partición canónica\(Q(N, V, T)\) es:
\[Q(N, V, T) = \dfrac{1}{N!h^{3N}} \int dx \: e^{-\beta \sum_{i=1}^N \textbf{p}_i^2/2m} \nonumber \]
Tenga en cuenta que esto se puede expresar como:
\[Q(N, V, T) = \dfrac{1}{N!h^{3N}}V^N \left[ \int dp \: e^{-\beta p^2/2m} \right]^{3N} \nonumber \]
Evaluar la integral gaussiana nos da el resultado final de inmediato:
\[Q(N, V, T) = \dfrac{1}{N!} \left[ \dfrac{V}{h^3} \left( \dfrac{2 \pi m}{\beta} \right)^{3/2} \right]^N \nonumber \]
Las expresiones para la energía:
\[E = -\dfrac{\partial}{\partial \beta} \: \text{ln} \: Q(N, V, T) \nonumber \]
que da:
\[E = \dfrac{3}{2}NkT = \dfrac{3}{2}nRT \label{Eq3.37} \]
y presión:
\[P = kT \left( \dfrac{\partial \: \text{ln} \: Q(N, V, T)}{\partial V} \right) \nonumber \]
dando:
\[P = \dfrac{NkT}{V} = \dfrac{nRT}{V} \label{Eq3.38} \]
que es la ley de gas ideal.