18.11: El principio de equipartición

El teorema de la equipartición, también conocida como la ley de equipartición, equipartición de energía o simplemente equipartición, establece que cada grado de libertad que aparece solo cuadráticamente en la energía total tiene una energía promedio de\(½k_BT\) en equilibrio térmico y contribuye\(½k_B\) al calor del sistema capacidad. Aquí,\(k_B\) está la constante de Boltzmann, y T es la temperatura en Kelvin. La ley de equipartición de la energía establece que cada término cuadrático en la expresión clásica para la energía aporta ½kBt a la energía promedio. Por ejemplo, el movimiento de un átomo tiene tres grados de libertad (número de formas de absorber energía), correspondientes a los componentes x, y y z de su impulso. Dado que estos momentos aparecen cuadráticamente en la energía cinética, cada átomo tiene una energía cinética promedio de\(3/2k_BT\) en equilibrio térmico. El número de grados de libertad de una molécula de gas poliatómico es\(3N\) donde\(N\) está el número de átomos en la molécula. Esto es igual al número de coordenadas para el sistema; por ejemplo, para dos átomos tendrías x, y, z para cada átomo.

Traducciones

La contribución traslacional a la energía promedio se deriva en términos de la derivada de la partición traslacional:

\[ \langle E_{trans} \rangle = - \dfrac{1}{q_{trans}} \dfrac{\partial q_{trans}}{\partial \beta} \label{Eq1} \]

Introduciendo la función de partición traslacional derivada anteriormente, la ecuación\(\ref{Eq1}\) se convierte

\[= - \dfrac{\Lambda^3}{V} \dfrac{\partial }{\partial \beta} \dfrac{V}{\Lambda^3} = - \dfrac{3}{\Lambda} \dfrac{\partial \Lambda}{\partial \beta} = \dfrac{3}{2} k_BT \nonumber \]

Así, los tres grados de libertad traslacionales en tres dimensiones satisfacen el teorema de equipartición con cada grado traslacional proporcionando\( ½ k_BT\) energía.

Rotaciones

Considerar las funciones de partición molecular. La energía rotacional promedio a la energía promedio se deriva en términos de la derivada de la partición traslacional:

\[ \langle E_{rot} \rangle = - \dfrac{1}{q_{rot}} \dfrac{\partial q_{rot}}{\partial \beta} \label{Eq2} \]

que cuando se introduce la función de partición rotacional, la ecuación\(\ref{Eq2}\) se convierte

\[ \langle E_{rot} \rangle = -\sigma \beta \tilde{B} \dfrac{1}{\sigma \tilde{B}} \dfrac{\partial}{\partial \beta} \dfrac{1}{\beta} = \dfrac{1}{\beta} = k_BT \nonumber \]

La expresión clásica de la energía rotacional de una molécula diatómica es

\[ E_{rot}^{(classical)}= \dfrac{1}{2} I (\omega_x^2 + \omega_y^2) \nonumber \]

donde\(I\) es el momento de inercia y\( \omega _x\) y\( \omega _y\) son las velocidades angulares en las\(y\) direcciones\(x\) y. La rotación a lo largo del eje molecular (el\(z\) eje aquí) no tiene sentido en la mecánica cuántica porque las rotaciones a lo largo del eje molecular conducen a configuraciones que son indistinguibles de la configuración original. Los dos grados de libertad rotacional han dado así un valor de\(kT\) con cada grado\( ½ k_BT\) de rotación proporcionando energía.

Vibraciones

Considera los movimientos vibracionales. La energía vibracional promedio a la energía promedio se deriva en términos de la derivada de la partición traslacional:

\[ \langle E_{vib} \rangle = - \dfrac{1}{q_{vib}} \dfrac{\partial q_{vib}}{\partial \beta} \label{Eq3} \]

que cuando se introduce la función de partición para la vibración, la ecuación\(\ref{Eq3}\) se convierte

\[ \langle E_{vib} \rangle = \dfrac{-1}{q_{vib}} \left( -hc\tilde{\nu}\dfrac{ e^{-hc \tilde{\nu}/k_BT}}{(1-e^{-hc \tilde{\nu}/k_BT})^2 } \right) = hc\tilde{\nu} \dfrac{ e^{-hc \tilde{\nu}/k_BT}}{\left(1-e^{-hc \tilde{\nu}/k_BT}\right) } \label{18.1.7} \]

Esto puede simplificarse dividiendo tanto el numerador como el denominador de la ecuación\(\ref{18.1.7}\) por\(e^{-hc \tilde{\nu}/k_BT}\)

\[\langle E_{vib} \rangle = hc \tilde{\nu} \left( \dfrac{ 1 }{e^{hc \tilde{\nu}/k_BT} -1} \right) \label{18.1.7B} \]

\(\ref{18.1.7B}\)La ecuación es aplicable a todas las temperaturas, pero si\( hc \tilde{\nu}/k_BT \ll 1\) (es decir, el límite de temperatura alta), entonces se puede expandir el exponencial en el denominador

\[ e^{hc \tilde{\nu}/k_BT} -1 \approx 1 + hc \tilde{\nu}/k_BT -1 = hc \tilde{\nu}/k_BT \label{expansion} \]

y la ecuación\(\ref{18.1.7B}\) se convierte

\[ \langle E_{vib} \rangle \approx \cancel{hc \tilde{\nu}} \left( \dfrac{1}{\cancel{ hc \tilde{\nu}}/k_BT}\right) \nonumber \]

\[ \langle E_{vib} \rangle \approx k_BT \label{18.1.10} \]

con cada grado vibracional proporcionando\( k_BT\) de energía (ya que hay ar dos términos cuadráticos en el hamiltoniano para un oscilador armónico (energía cinética y energía potencial).

Comparar Ecuación\(\ref{18.1.10}\) con la expresión clásica para la energía vibratoria

\[ E_{vib}^{(classical)} = ½ kx^2 + ½ μv_x^2 \nonumber \]

A alta temperatura el teorema de equipartición es válido, pero a baja temperatura, la expansión en Ecuación\(\ref{expansion}\) falla (o se requieren más términos). En este caso, solo se ocupan unos pocos estados vibracionales y el principio de equipartición no suele ser aplicable.

Capacidad de Calor

Capacidad calorífica a volumen constante\(C_v\), se define como

\[ C_v = \left(\dfrac{\partial U}{\partial T} \right)_v \nonumber \]

El teorema de equipartición requiere que cada grado de libertad que aparece sólo cuadráticamente en la energía total tenga una energía promedio de ½k _B T en equilibrio térmico y, así, contribuya ½kB a la capacidad calorífica del sistema. Así, cada uno de los tres grados de libertad traslacional aporta ½R a (3/2 R). La contribución de la energía cinética rotacional será R para las moléculas lineales y 3/2R para las moléculas no lineales. Para la vibración, un oscilador tiene términos cuadráticos cinéticos y potenciales, haciendo la contribución de cada modo vibracional R. Sin embargo, k _B T tiene que ser mucho mayor que el espaciamiento entre los niveles de energía cuántica. Si esto no se satisface, se reducirá la capacidad calorífica y que bajará a cero a bajas temperaturas. Se dice que el grado de libertad correspondiente está congelado; esta es la situación de los grados vibracionales de libertad a temperatura ambiente y por eso la suposición habitual es que no van a contribuir.

Figura 18.11.1 : Gráfica idealizada del calor específico molar de un gas diatómico frente a la temperatura. Concuerda con el valor (7/2) R predicho por equipartición a altas temperaturas (donde R es la constante del gas), pero disminuye a (5/2) R y luego (3/2) R a temperaturas más bajas, ya que los modos de movimiento vibracional y rotacional se “congelan”. El fracaso del teorema de equipartición condujo a una paradoja que solo fue resuelta por la mecánica cuántica. Para la mayoría de las moléculas, la temperatura de transición T _pudrición es mucho menor que la temperatura ambiente, mientras que T _vib puede ser diez veces mayor o más. Un ejemplo típico es el monóxido de carbono, CO, para el cual T _rot ≈ 2.8 K y T _vib ≈ 3103 K. Para moléculas con átomos muy grandes o débilmente unidos, T _vib puede estar cerca de la temperatura ambiente (aproximadamente 300 K); por ejemplo, T _vib ≈ 308 K para gas yodo, I ₂. (Dominio público; Pd-Self)

Ejemplo: CO ₂ vs NO ₂

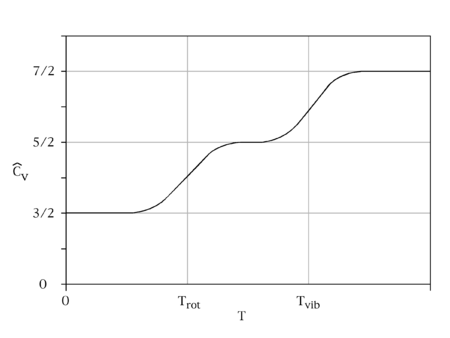
Para comparar las capacidades térmicas molares de dióxido de nitrógeno y dióxido de carbono a volumen constante (a temperatura ambiente), usemos la ley de equipartición y supongamos que las vibraciones se congelarán a temperatura ambiente. El molar predicho para el lineal\(CO_2\) (con tres grados de libertad de traslación y dos rotacionales) es\(5/2R\)\(20.8\, JK^{-1}mo'^{-1})\).

El molar estimado para\(NO_2\) (una molécula doblada, con tres grados de libertad de traslación y tres rotacionales) es\(3R \,(25.0\, JK^{-1}mol^{-1})\). Estas estimaciones se acercan a los valores experimentales:

• 30.1 JK ^-1 mol ^-1 para\(CO_2\)
• 29.5 JK ^-1 mol ^-1 para\(NO_2\)

Especialmente para\(CO_2\), la desviación es significativa. Esto sugiere que, aunque no todos los grados de libertad vibracional están disponibles, no pueden ser ignorados por completo. La mayor desviación en la predicción de las capacidades térmicas molares se debe probablemente a la existencia de la menor vibración de flexión de frecuencia en el dióxido de carbono.

Referencias

1. Termodinámica y Mecánica Estadística, Greiner W., Neise, Stocker, Springer, 2001
2. Química Física, 5ª ed., Atkins P., W. H. Freeman and Company, 1994.

Colaboradores y Atribuciones

• Zane Sterkewolf (UC Davis)
• www.chem.iitb.ac.in/~bltembe/pdfs/ch_3.pdf
• Sudarson S Sinha (Universidad de Tel Aviv)