20.4: La Segunda Ley de la Termodinámica

Espontaneidad de un sistema aislado

Un sistema aislado es un poco más que solo adiabático. En este último el calor no puede entrar ni salir. En un sistema aislado nada entra o sale nada, ni calor ni masa ni siquiera radiación alguna, como la luz. El sistema aislado es como un pequeño universo para sí mismo.

Consideremos un proceso de ley cero. Tenemos dos bloques idénticos de metal, digamos aluminio. Cada uno se encuentra en equilibrio térmico, pero a diferentes temperaturas. Se ponen en contacto entre sí pero aislados del resto del universo.

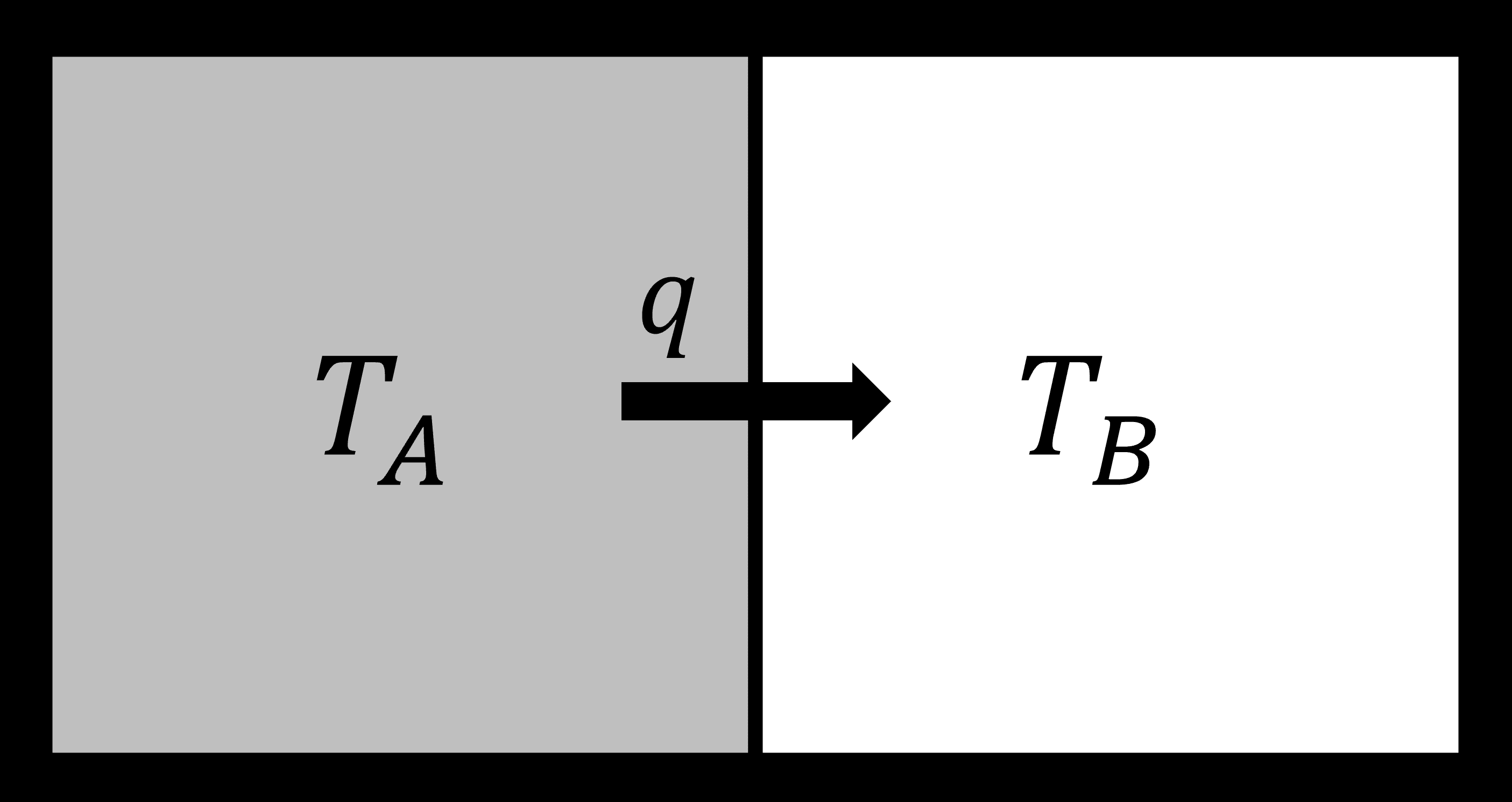
• Ley cero: El calor fluirá de caliente a frío
• Primera ley: No hay cambio en la energía total

por lo que:

\[dU_A= -dU_B \nonumber \]

Tampoco hay trabajo por lo que:

\[dU_A = \delta q_A + 0 \nonumber \]

Debido a que U es una función de estado esto hace que\(q\) una función de estado también, de lo contrario esta igualdad no se sostiene. Como solo hay un término a la derecha solo hay un camino (a lo largo de q). Entonces podríamos escribir:

\[dU_A = dq_A \nonumber \]

Esto implica que no necesitamos preocuparnos por caminos reversibles e irreversibles ya que solo hay un camino. Desde:

\[dS = \dfrac{\delta q_{rev}}{T} \nonumber \]

En este caso particular:

\[TdS = \delta q_{rev} = dU \nonumber \]

Así conseguimos:

\[ dS = \dfrac{dU_A}{T_A} + \dfrac{dU_B}{T_B} = \dfrac{dU_A}{T_A} - \dfrac{dU_A}{T_B} = dU_A \left( \dfrac{1}{T_A} - \dfrac{1}{T_B} \right) \nonumber \]

Claramente mientras las dos temperaturas no sean iguales no\(dS\) es cero y la entropía no se conserva. En cambio va en aumento. Con el tiempo, las temperaturas se volverán iguales (si los bloques son idénticos, la temperatura final es la media de\(T_A\) y\(T_B\)) y la entropía alcanzará un máximo.

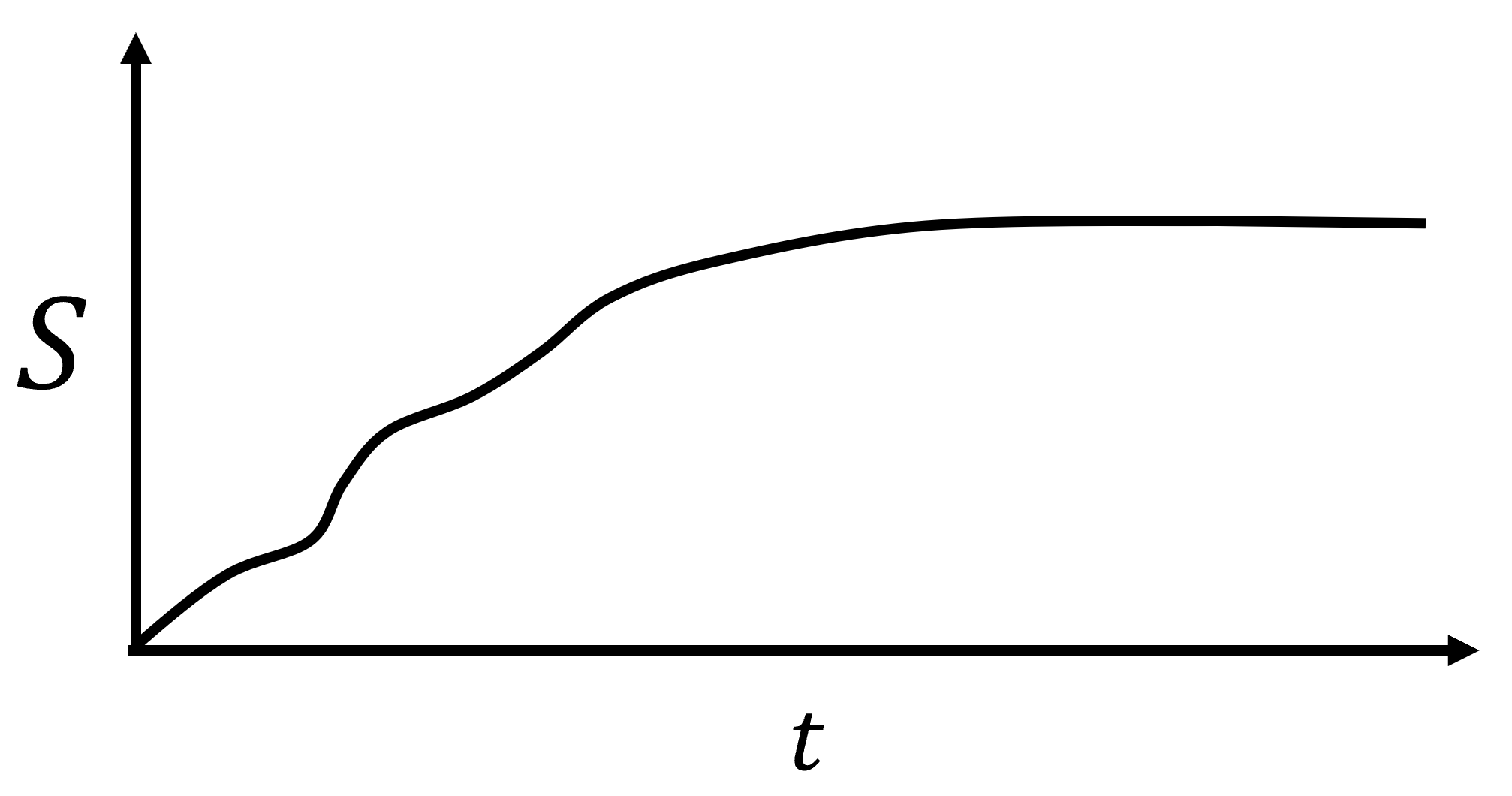
Para nuestros dos bloques idénticos de metal (con la misma capacidad calorífica,\(C_V\)), podemos, de hecho, derivar que la entropía cambia:

\[\Delta S = C_V \ln \left[\dfrac{T_A^2 + T_B^2}{4T_AT_B}\right]. \nonumber \]

Esta es, efectivamente, una cantidad positiva. En general, podemos decir para un sistema aislado:

\[dS \ge 0 \nonumber \]

Así, si estamos ante un proceso espontáneo (y aislado)\(dS >0\) y se está produciendo entropía. Esto nos da un criterio de espontaneidad.

Intercambio de entropía de un sistema abierto

En un sistema aislado\(dS\) representa la entropía producida\(dS_{prod}\) y este es un buen criterio para la espontaneidad. Por supuesto el requisito de que el sistema esté aislado es muy restrictivo y hace que el criterio sea tan bueno como inútil... ¿Qué sucede en un sistema que puede intercambiar calor con el resto del universo? Nosotros sí tenemos cambios de entropía en ese caso, pero parte de ellos puede que no tengan nada que ver con la producción, porque también tenemos que considerar el calor que se intercambia.

\[dS = dS_{prod} + dS_{exchange} \nonumber \]

Si el proceso es reversible (eso es completamente no espontáneo) estamos tratando de\(\delta q_{rev}\) manera que\(dS_{exchange} = \delta q_{rev} /T\), pero eso es también lo que\(dS_{tot}\) es igual a (por definición). Esto no deja espacio para la producción de entropía.

Así que tenemos:

Aislado:\(dS = dS_{prod} + 0\)

Reversible\(dS = 0 + \delta q_{rev}/T\)

Observe que esto demuestra que para los sistemas no aislados el cambio de entropía no es un buen criterio para la espontaneidad en absoluto... En el caso de que el intercambio de calor sea irreversible parte de la entropía es la producción de entropía por parte del sistema:

Irreversibles:\(dS = dS_{prod} + \delta q_{irrev}/T\)

\(dS > \delta q_{irrev}/T\)en este caso.

Generalizando los casos aislados, irreversibles y reversibles podemos decir:

\[dS \ge \dfrac{δq}{T} \nonumber \]

Esta es la desigualdad de Clausius.