20.6: Siempre debemos idear un proceso reversible para calcular los cambios de entropía

La segunda ley de la termodinámica se puede formular de muchas maneras, pero de una forma u otra todas están relacionadas con el hecho de que la entropía de la función estatal,\(S\), tiende a aumentar con el tiempo en sistemas aislados. Desde hace mucho tiempo, la gente ha mirado al universo entero como un ejemplo de un sistema aislado y concluyó que su entropía debe ir aumentando de manera constante hasta llegar\(\delta S_{universe}\) a ser cero. Como veremos a continuación, la segunda ley tiene importantes consecuencias para la cuestión de cómo podemos usar el calor para hacer un trabajo útil.

Últimamente, cosmólogos como Hawkins han comenzado a cuestionar la suposición de que la entropía del universo va en constante aumento. El problema clave es el papel que juegan la gravedad y la relatividad en la creación de agujeros negros.

Expansión de vacío

Comparemos dos expansiones de\(V_1\) a\(V_2\) para un gas ideal, ambas son isotérmicas. El primero es irreversible, donde tiramos de una clavija y dejamos que el pistón se mueva contra el vacío:

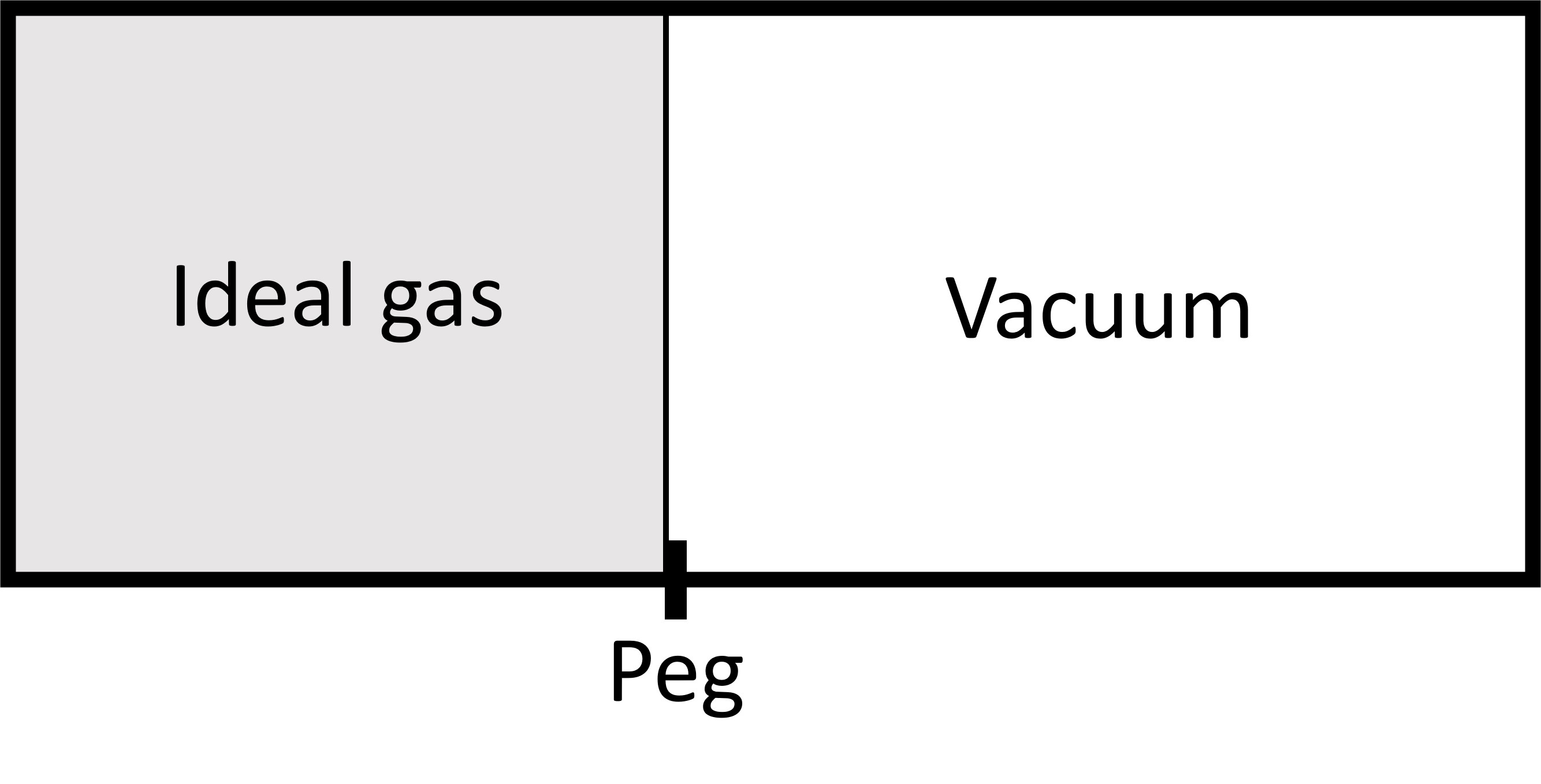
El segundo es una expansión isotérmica reversible de\(V_1\) a\(V_2\) (y\(P_1\) a\(P_2\)) que hemos examinado antes. En ambos casos, el no hay cambio en la energía porque\(T\) no cambia; sin embargo, durante la expansión irreversible, tampoco hay trabajo de volumen porque

\[\int -P_{ext}dV = 0 \nonumber \]

se integra a cero. El pistón no tiene nada contra lo que realizar trabajos hasta que se estrelle contra la pared derecha. En este punto\(V=V_2\) y luego\(dV\) se convierte en cero.

¡Sin energía y sin trabajo significa que no hay calor!

Claramente el calor cero es calor irreversible (\(q_{irr} = 0\)) y esto dificulta el cálculo de la entropía de este proceso espontáneo. Pero entonces este proceso termina en el mismo estado final que la expansión reversible de\(V_1\) a\(V_2\). Sabemos que sigue\(dU\) siendo cero, pero ahora\(δw_{rev} = -δq_{rev}\) es distinto de cero. Calculamos su valor antes de:

\[q_{rev} = nRT \ln \left(\dfrac{V_2}{V_1} \right) \label{Vacuum} \]

Para encontrar solo\(\Delta S\) podemos dividir la ecuación\(\ref{Vacuum}\) por la temperatura (constante):

\[\Delta S= nR \ln \left(\dfrac{V_2}{V_1} \right) \nonumber \]

Como\(S\) es una función de estado, esta ecuación también se mantiene para la expansión irreversible contra el vacío.

Calcule siempre la diferencia de entropía entre dos puntos a lo largo de una trayectoria reversible.

Para la expansión irreversible al vacío vemos que

\[\Delta S_{total} = \Delta S_{sys} + \Delta S_{surr} = nR\ln \left( \dfrac{V_2}{V_1}\right) + 0 \nonumber \]

Para el reversible:

\[\Delta S_{total} = \Delta S_{sys} + \Delta S_{surr} = 0+ nR\ln \left( \dfrac{V_2}{V_1}\right) \nonumber \]

La mezcla de dos gases

Considera dos gases ideales a la misma presión separados por una pared delgada que se perfora. Ambos gases se comportan como si el otro no estuviera ahí y nuevamente obtenemos un proceso espontáneo, mezclando en este caso.

Si la presión es la misma el número de moles de cada gas debe ser proporcional a los volúmenes originales,\(V_A\) y\(V_B\), y el número total de moles al volumen total\(V_{tot}\).

Para el gas A podemos escribir:

\[\Delta S_A = n_A R \ln \dfrac{V_{tot}}{V_A} = n_A R \ln \dfrac{n_{tot}}{n_A} \nonumber \]

y de manera similar para el gas B podemos escribir:

\[\Delta S_B = n_B R \ln \dfrac{V_{tot}}{V_B} = n_B R \ln \dfrac{n_{tot}}{n_B} \nonumber \]

El cambio de entropía total es, por lo tanto, la suma de los cambios de entropía constituyentes:

\[ \Delta S = \Delta S_A + \Delta S_B \nonumber \]

y el cambio de entropía total por mol de gas es:

\[ \dfrac{\Delta S}{n_{tot}} =R \dfrac{\left[n_B \ln \dfrac{n_{tot}}{n_B}+ n_A \ln \dfrac{n_{tot}}{n_A} \right ]}{n_{tot}} \label{EqTot} \]

La ecuación se\(\ref{EqTot}\) puede simplificar usando fracciones molares:

\[\chi_A = \dfrac{n_A}{n_{tot}} \nonumber \]

y la relación matemática de logaritmos que:

\[\ln \left( \dfrac{x}{y} \right)= - \ln \left( \dfrac{y}{x} \right) \nonumber \]

a:

\[\Delta \bar{S} = -R \left [\chi_A\ln \chi_A +\chi_B \ln \chi_B \right] \label{Molar Entropy} \]

En el caso de mezcla de más de dos gases, la Ecuación se\(\ref{Molar Entropy}\) puede expresar como:

\[\Delta \bar{S} = -R \sum \chi_i\ln \chi_i \label{Sum Entropy} \]

Esta entropía se expresa en Ecuaciones\(\ref{Molar Entropy}\) y\(\ref{Sum Entropy}\) se conoce como la entropía de la mezcla; su existencia es la razón principal por la que existe tal cosa como la difusión y la mezcla cuando los gases, pero también las soluciones (incluso las sólidas) se ponen en contacto entre sí.