23.4: La Ecuación Clausius-Clapeyron
- Page ID
- 79638
Evaporación
En la Sección 23.3, se derivó la Ecuación de Clapeyron para los puntos de fusión.
\[\dfrac{dP}{dT} = \dfrac{ΔH_{molar}}{TΔV_{molar}} \nonumber \]
Sin embargo, nuestro argumento es en realidad bastante general y también debería sostenerse para los equilibrios de vapor. El único problema es que el volumen molar de gases no es de ninguna manera tan bien constante como lo son para las fases condensadas. (i. e., para condensa fases, ambas\(α\) y\(κ\) son bastante pequeñas).
Podemos escribir:
\[\dfrac{dP}{dT} =\dfrac{ ΔH_{molar}}{TΔV_{molar}} = \dfrac{ΔH_{molar}}{T} \left[V_{molar}^{gas}-V_{molar}^{liquid} \right] \nonumber \]
como
\[V_{molar}^{gas} \gg V_{molar}^{liquid} \nonumber \]
podemos aproximar
\[V_{molar}^{gas}-V_{molar}^{liquid} \nonumber \]
simplemente tomando\(V_{molar}^{gas}\). Más aún si el vapor se considera un gas ideal, entonces
\[V_{molar}^{gas} = \dfrac{RT}{P} \nonumber \]
Obtenemos
\[\dfrac{1}{P} .\dfrac{dP}{dT} = \dfrac{d \ln P}{dT} = \dfrac{ΔH_{molar}^{vap}}{RT^2} \label{CCe} \]
\(\ref{CCe}\)La ecuación se conoce como la ecuación de Clausius-Clapeyron. Podemos seguir trabajando nuestra integración y encontrar cómo cambia la presión de vapor de equilibrio con la temperatura:
\[\ln \left( \dfrac{P_2}{P_1} \right)= \dfrac{-ΔH_{molar}^{vap}}{R} \left[\dfrac{1}{T_2}-\dfrac{1}{T_1} \right] \nonumber \]
Así, si conocemos la entalpía molar de vaporización podemos predecir las líneas de vapor en el diagrama. Por supuesto, es probable que las aproximaciones hechas conduzcan a desviaciones si el vapor no es ideal o muy denso (por ejemplo, acercándose al punto crítico).
La ecuación de Clapeyron
El Clapeyron intenta responder a la pregunta de cuál es la forma de una línea de coexistencia bifásica. En el\(P-T\) plano, vemos la función a\(P(T)\), que nos da la\(P\) dependencia de\(T\) a lo largo de una curva de convivencia.
Considerar dos fases, denotadas\(\alpha\) y\(\beta\), en equilibrio entre sí. Estos podrían ser sólidos y líquidos, líquidos y gaseosos, sólidos y gaseosos, dos fases sólidas, et. Dejar\(\mu_\alpha (P, T)\) y\(\mu_\beta (P, T)\) ser los potenciales químicos de las dos fases. Acabamos de ver que
\[\mu_\alpha (P, T) = \mu_\beta (P, T) \label{14.1}\]
A continuación, supongamos que la presión y la temperatura se cambian por\(dP\) y\(dT\). Los cambios en los potenciales químicos de cada fase son
\[ d \mu_{\alpha} (P, T) = d \mu_{\beta} (P, T) \label{14.2a}\]
\[\left( \dfrac{\partial \mu_{\alpha}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\alpha}}{\partial T} \right)_P dT = \left( \dfrac{\partial \mu_{\beta}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\beta}}{\partial T} \right)_P dT \label{14.2b}\]
Sin embargo\(G(n, P, T) = n \mu (P, T)\), ya que, la energía libre molar\(\bar{G} (P, T)\)\(G(n, P, T)/n\), que es, también es igual al potencial químico
\[\bar{G} (P, T) = \dfrac{G(n, P, T)}{n} = \mu (P, T) \label{14.3}\]
Además, los derivados de\(\bar{G}\) son
\[\left( \dfrac{\partial \bar{G}}{\partial P} \right)_T = \bar{V}, \: \: \: \: \: \: \: \left( \dfrac{\partial \bar{G}}{\partial T} \right)_P = -\bar{S} \label{14.4}\]
Aplicando estos resultados a la condición de potencial químico en Ecuación\(\ref{14.2b}\), obtenemos
\ [\ begin {align}\ izquierda (\ dfrac {\ parcial\ bar {G} _\ alfa} {\ P parcial}\ derecha) _T dP +\ izquierda (\ dfrac {\ parcial\ bar {G} _\ alfa} {\ T parcial}\ derecha) _P dT &=\ izquierda (\ dfrac {\ parcial\ bar {G} _\ beta} {\ P parcial}\ derecha) _T dP +\ izquierda (\ dfrac {\ parcial\ bar {G} _\ beta} {\ T parcial}\ derecha) _P dT\
\[5pt] \bar{V}_\alpha dP - \bar{S}_\alpha dT &= \bar{V}_\beta dP - \bar{S}_\beta dT \end{align} \label{14.5}\]
Dividiendo por\(dT\), obtenemos
\ [\ comenzar {alinear}\ bar {V} _\ alfa\ dfrac {\ P parcial} {\ T parcial} -\ barra {S} _\ alfa &=\ bar {V} _ _\ beta\ dfrac {\ P parcial} {\ T parcial} -\ barra {S} _ _\ beta\
\ [5pt] (\ bar {V} _ _\ alfa -\ bar {V} _\ beta)\ dfrac {\ P parcial} {\ T parcial} &=\ barra {S} _\ alfa -\ bar {S} _\ beta\
\[5pt] \dfrac{dP}{dT} &= \dfrac{\bar{S}_\alpha - \bar{S}_\beta}{\bar{V}_\alpha - \bar{V}_\beta} \end{align} \label{14.6}\]
La importancia de la cantidad\(dP/dT\) es que representa la pendiente de la curva de coexistencia en el diagrama de fases entre las dos fases. Ahora, en equilibrio\(dG = 0\), y desde entonces\(G = H - TS\), se deduce que\(dH = T \: dS\) a fijo\(T\). En el estrecho rango de temperatura en el que las dos fases están en equilibrio, podemos suponer que\(H\) es independiente de\(T\), por lo tanto, podemos escribir\(S = H/T\). En consecuencia, podemos escribir la diferencia de entropía molar como
\[\bar{S}_\alpha - \bar{S}_\beta = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T} \label{14.7}\]
y la derivada de la presión\(dP/dT\) se convierte en
\[\dfrac{dP}{dT} = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T (\bar{V}_\alpha - \bar{V}_\beta)} = \dfrac{\Delta_{\alpha \beta} \bar{H}}{T \Delta_{\alpha \beta} \bar{V}} \label{14.8}\]
un resultado conocido como la ecuación de Clapeyron, que nos dice que la pendiente de la curva de coexistencia está relacionada con la relación de la entalpía molar entre las fases al cambio en el volumen molar entre las fases. Si el equilibrio de fases es entre las fases sólida y líquida, entonces\(\Delta_{\alpha \beta} \bar{H}\) y\(\Delta_{\alpha \beta} \bar{V}\) son\(\Delta \bar{H}_\text{fus}\) y\(\Delta \bar{V}_\text{fus}\), respectivamente. Si el equilibrio de fase es entre las fases líquida y gaseosa, entonces\(\Delta_{\alpha \beta} \bar{H}\) y\(\Delta_{\alpha \beta} \bar{V}\) son\(\Delta \bar{H}_\text{vap}\) y\(\Delta \bar{V}_\text{vap}\), respectivamente.
Para el equilibrio líquido-gas, se pueden hacer algunas aproximaciones interesantes en el uso de la ecuación de Clapeyron. Para este equilibrio, la ecuación\(\ref{14.8}\) se convierte en
\[\dfrac{dP}{dT} = \dfrac{\Delta \bar{H}_\text{vap}}{T (\bar{V}_g - \bar{V}_l)} \label{14.9}\]
En este caso,\(\bar{V}_g \gg \bar{V}_l\), y podemos aproximar la Ecuación\(\ref{14.9}\) como
\[\dfrac{dP}{dT} \approx \dfrac{\Delta \bar{H}_\text{vap}}{T \bar{V}_g} \label{14.10}\]
Supongamos que podemos tratar la fase vapor como un gas ideal. Ciertamente, esta no es una buena aproximación tan cercana al punto de vaporización, pero lleva a un ejemplo que podemos integrar. Dado que\(PV_g = nRT\),\(P \bar{V}_g = RT\), La ecuación\(\ref{14.10}\) se convierte
\ [\ begin {align}\ dfrac {dP} {dT} &=\ dfrac {\ Delta\ bar {H} _\ texto {vap} P} {RT^2}\
\ [5pt]\ dfrac {1} {P}\ dfrac {dP} {dT} &=\ dfrac {\ Delta\ bar {H} _ _\ texto {vap}} {RT^2}\
\[5pt] \dfrac{d \: \text{ln} \: P}{dT} &= \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} \end{align} \label{14.11}\]
que se llama la ecuación Clausius-Clapeyron. Ahora integramos ambos lados, lo que rinde
\[\text{ln} \: P = -\dfrac{\Delta \bar{H}_\text{vap}}{RT} + C\]
donde\(C\) es una constante de integración. Exponenciando ambos lados, encontramos
\[P(T) = C' e^{-\Delta \bar{H}_\text{vap}/RT}\]
que en realidad tiene la curvatura incorrecta para grandes\(T\), pero como la línea de coexistencia líquido-vapor termina en un punto crítico, siempre y cuando no\(T\) sea demasiado grande, la aproximación que conduce a la expresión anterior no es tan mala.
Si nosotros, en cambio, integramos ambos lados, la izquierda de\(P_1\) a\(P_2\), y la derecha de\(T_1\) a\(T_2\), encontramos
\ [\ begin {align}\ int_ {P_1} ^ {P_2} d\:\ text {ln}\: P &=\ int_ {T_1} ^ {T_2}\ dfrac {\ Delta\ bar {H} _\ texto {vap}} {RT^2} dT\
\ [5pt]\ texto {ln}\:\ izquierda (\ dfrac {P_2} {P_1}\ derecha) &= -\ dfrac {\ Delta\ bar {H} _\ texto {vap}} {R}\ izquierda (\ dfrac {1} {T_2} -\ dfrac {1} {T_1}\ derecha)\
\[5pt] &= \dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{T_1 - T_1}{T_1 T_2} \right) \end{align} \label{14.12}\]
asumiendo que\(\Delta \bar{H}_\text{vap}\) es independiente de\(T\). Aquí\(P_1\) está la presión de la fase líquida, y\(P_2\) es la presión de la fase de vapor. Supongamos que sabemos\(P_2\) a una temperatura\(T_2\), y queremos saber\(P_3\) a otra temperatura\(T_3\). El resultado anterior se puede escribir como
\[\text{ln} \: \left( \dfrac{P_3}{P_1} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_3} - \dfrac{1}{T_1} \right) \label{14.13}\]
Al restar los dos resultados, obtenemos
\[\text{ln} \: \left( \dfrac{P_2}{P_3} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_3} \right) \label{14.14}\]
para que podamos determinar la presión de vapor a cualquier temperatura si se conoce como una temperatura.
Para ilustrar el uso de este resultado, considere el siguiente ejemplo:
A\(1 \: \text{bar}\), el punto de ebullición del agua es\(373 \: \text{K}\). ¿A qué presión hierve el agua\(473 \: \text{K}\)? Tomar el calor de vaporización del agua para ser\(40.65 \: \text{kJ/mol}\).
Solución
Dejar\(P_1 = 1 \: \text{bar}\) y\(T_1 = 373 \: \text{K}\). Toma\(T_2 = 473 \: \text{K}\), y tenemos que calcular\(P_2\). Sustituyendo en los números, encontramos
\ [\ begin {align}\ text {ln}\: P_2 (\ text {bar}) &= -\ dfrac {(40.65\:\ text {kj/mol}) (1000\:\ text {J/kJ})} {8.3145\:\ text {J/mol}\ cdot\ text {K}}\ left (\ dfrac {1} {473\:\ texto {K}} -\ dfrac {1} {373\:\ texto {K}}\ derecha) = 2.77\
\[5pt] P_2(\text{bar}) &= (1 \: \text{bar}) \: e^{2.77} = 16 \: \text{bar} \end{align}\]
La ecuación de Clapeyron
El Clapeyron intenta responder a la pregunta de cuál es la forma de una línea de coexistencia bifásica. En el\(P-T\) plano, vemos la función a\(P(T)\), que nos da la\(P\) dependencia de\(T\) a lo largo de una curva de convivencia.
Considerar dos fases, denotadas\(\alpha\) y\(\beta\), en equilibrio entre sí. Estos podrían ser sólidos y líquidos, líquidos y gaseosos, sólidos y gaseosos, dos fases sólidas, et. Dejar\(\mu_\alpha (P, T)\) y\(\mu_\beta (P, T)\) ser los potenciales químicos de las dos fases. Acabamos de ver que
\[\mu_\alpha (P, T) = \mu_\beta (P, T) \label{14.1} \]
A continuación, supongamos que la presión y la temperatura se cambian por\(dP\) y\(dT\). Los cambios en los potenciales químicos de cada fase son
\[ d \mu_{\alpha} (P, T) = d \mu_{\beta} (P, T) \label{14.2a} \]
\[\left( \dfrac{\partial \mu_{\alpha}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\alpha}}{\partial T} \right)_P dT = \left( \dfrac{\partial \mu_{\beta}}{\partial P} \right)_T dP + \left( \dfrac{\partial \mu_{\beta}}{\partial T} \right)_P dT \label{14.2b} \]
Sin embargo\(G(n, P, T) = n \mu (P, T)\), ya que, la energía libre molar\(\bar{G} (P, T)\)\(G(n, P, T)/n\), que es, también es igual al potencial químico
\[\bar{G} (P, T) = \dfrac{G(n, P, T)}{n} = \mu (P, T) \label{14.3} \]
Además, los derivados de\(\bar{G}\) son
\[\left( \dfrac{\partial \bar{G}}{\partial P} \right)_T = \bar{V}, \: \: \: \: \: \: \: \left( \dfrac{\partial \bar{G}}{\partial T} \right)_P = -\bar{S} \label{14.4} \]
Aplicando estos resultados a la condición de potencial químico en Ecuación\(\ref{14.2b}\), obtenemos
\[\begin{align} \left( \dfrac{\partial \bar{G}_\alpha}{\partial P} \right)_T dP + \left( \dfrac{\partial \bar{G}_\alpha}{\partial T} \right)_P dT &= \left( \dfrac{\partial \bar{G}_\beta}{\partial P} \right)_T dP + \left( \dfrac{\partial \bar{G}_\beta}{\partial T} \right)_P dT \\[5pt] \bar{V}_\alpha dP - \bar{S}_\alpha dT &= \bar{V}_\beta dP - \bar{S}_\beta dT \end{align} \label{14.5} \]
Dividiendo por\(dT\), obtenemos
\[\begin{align} \bar{V}_\alpha \dfrac{\partial P}{\partial T} - \bar{S}_\alpha &= \bar{V}_\beta \dfrac{\partial P}{\partial T} - \bar{S}_\beta \\[5pt] (\bar{V}_\alpha - \bar{V}_\beta) \dfrac{\partial P}{\partial T} &= \bar{S}_\alpha - \bar{S}_\beta \\[5pt] \dfrac{dP}{dT} &= \dfrac{\bar{S}_\alpha - \bar{S}_\beta}{\bar{V}_\alpha - \bar{V}_\beta} \end{align} \label{14.6} \]
La importancia de la cantidad\(dP/dT\) es que representa la pendiente de la curva de coexistencia en el diagrama de fases entre las dos fases. Ahora, en equilibrio\(dG = 0\), y desde entonces\(G = H - TS\), se deduce que\(dH = T \: dS\) a fijo\(T\). En el estrecho rango de temperatura en el que las dos fases están en equilibrio, podemos suponer que\(H\) es independiente de\(T\), por lo tanto, podemos escribir\(S = H/T\). En consecuencia, podemos escribir la diferencia de entropía molar como
\[\bar{S}_\alpha - \bar{S}_\beta = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T} \label{14.7} \]
y la derivada de la presión\(dP/dT\) se convierte en
\[\dfrac{dP}{dT} = \dfrac{\bar{H}_\alpha - \bar{H}_\beta}{T (\bar{V}_\alpha - \bar{V}_\beta)} = \dfrac{\Delta_{\alpha \beta} \bar{H}}{T \Delta_{\alpha \beta} \bar{V}} \label{14.8} \]
un resultado conocido como la ecuación de Clapeyron, que nos dice que la pendiente de la curva de coexistencia está relacionada con la relación de la entalpía molar entre las fases al cambio en el volumen molar entre las fases. Si el equilibrio de fases es entre las fases sólida y líquida, entonces\(\Delta_{\alpha \beta} \bar{H}\) y\(\Delta_{\alpha \beta} \bar{V}\) son\(\Delta \bar{H}_\text{fus}\) y\(\Delta \bar{V}_\text{fus}\), respectivamente. Si el equilibrio de fase es entre las fases líquida y gaseosa, entonces\(\Delta_{\alpha \beta} \bar{H}\) y\(\Delta_{\alpha \beta} \bar{V}\) son\(\Delta \bar{H}_\text{vap}\) y\(\Delta \bar{V}_\text{vap}\), respectivamente.
Para el equilibrio líquido-gas, se pueden hacer algunas aproximaciones interesantes en el uso de la ecuación de Clapeyron. Para este equilibrio, la ecuación\(\ref{14.8}\) se convierte en
\[\dfrac{dP}{dT} = \dfrac{\Delta \bar{H}_\text{vap}}{T (\bar{V}_g - \bar{V}_l)} \label{14.9} \]
En este caso,\(\bar{V}_g \gg \bar{V}_l\), y podemos aproximar la Ecuación\(\ref{14.9}\) como
\[\dfrac{dP}{dT} \approx \dfrac{\Delta \bar{H}_\text{vap}}{T \bar{V}_g} \label{14.10} \]
Supongamos que podemos tratar la fase vapor como un gas ideal. Ciertamente, esta no es una buena aproximación tan cercana al punto de vaporización, pero lleva a un ejemplo que podemos integrar. Dado que\(PV_g = nRT\),\(P \bar{V}_g = RT\), La ecuación\(\ref{14.10}\) se convierte
\[\begin{align} \dfrac{dP}{dT} &= \dfrac{\Delta \bar{H}_\text{vap} P}{RT^2} \\[5pt] \dfrac{1}{P} \dfrac{dP}{dT} &= \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} \\[5pt] \dfrac{d \: \text{ln} \: P}{dT} &= \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} \end{align} \label{14.11} \]
que se llama la ecuación Clausius-Clapeyron. Ahora integramos ambos lados, lo que rinde
\[\text{ln} \: P = -\dfrac{\Delta \bar{H}_\text{vap}}{RT} + C \nonumber \]
donde\(C\) es una constante de integración. Exponenciando ambos lados, encontramos
\[P(T) = C' e^{-\Delta \bar{H}_\text{vap}/RT} \nonumber \]
que en realidad tiene la curvatura incorrecta para grandes\(T\), pero como la línea de coexistencia líquido-vapor termina en un punto crítico, siempre y cuando no\(T\) sea demasiado grande, la aproximación que conduce a la expresión anterior no es tan mala.
Si nosotros, en cambio, integramos ambos lados, la izquierda de\(P_1\) a\(P_2\), y la derecha de\(T_1\) a\(T_2\), encontramos
\[\begin{align} \int_{P_1}^{P_2} d \: \text{ln} \: P &= \int_{T_1}^{T_2} \dfrac{\Delta \bar{H}_\text{vap}}{RT^2} dT \\[5pt] \text{ln} \: \left( \dfrac{P_2}{P_1} \right) &= -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_1} \right) \\[5pt] &= \dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{T_1 - T_1}{T_1 T_2} \right) \end{align} \label{14.12} \]
asumiendo que\(\Delta \bar{H}_\text{vap}\) es independiente de\(T\). Aquí\(P_1\) está la presión de la fase líquida, y\(P_2\) es la presión de la fase de vapor. Supongamos que sabemos\(P_2\) a una temperatura\(T_2\), y queremos saber\(P_3\) a otra temperatura\(T_3\). El resultado anterior se puede escribir como
\[\text{ln} \: \left( \dfrac{P_3}{P_1} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_3} - \dfrac{1}{T_1} \right) \label{14.13} \]
Al restar los dos resultados, obtenemos
\[\text{ln} \: \left( \dfrac{P_2}{P_3} \right) = -\dfrac{\Delta \bar{H}_\text{vap}}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_3} \right) \label{14.14} \]
para que podamos determinar la presión de vapor a cualquier temperatura si se conoce como una temperatura.
Para ilustrar el uso de este resultado, considere el siguiente ejemplo:
A\(1 \: \text{bar}\), el punto de ebullición del agua es\(373 \: \text{K}\). ¿A qué presión hierve el agua\(473 \: \text{K}\)? Tomar el calor de vaporización del agua para ser\(40.65 \: \text{kJ/mol}\).
Solución
Dejar\(P_1 = 1 \: \text{bar}\) y\(T_1 = 373 \: \text{K}\). Toma\(T_2 = 473 \: \text{K}\), y tenemos que calcular\(P_2\). Sustituyendo en los números, encontramos
\[\begin{align} \text{ln} \: P_2(\text{bar}) &= -\dfrac{(40.65 \: \text{kJ/mol})(1000 \: \text{J/kJ})}{8.3145 \: \text{J/mol} \cdot \text{K}} \left( \dfrac{1}{473 \: \text{K}} - \dfrac{1}{373 \: \text{K}} \right) = 2.77 \\[5pt] P_2(\text{bar}) &= (1 \: \text{bar}) \: e^{2.77} = 16 \: \text{bar} \end{align} \nonumber \]
- Aplicar la ecuación Clausius-Clapeyron para estimar la presión de vapor a cualquier temperatura.
- Estimar el calor de transición de fase a partir de las presiones de vapor medidas a dos temperaturas.
Las curvas de vaporización de la mayoría de los líquidos tienen formas similares con la presión de vapor aumentando constantemente a medida que aumenta la temperatura (Figura\(\PageIndex{1}\)).
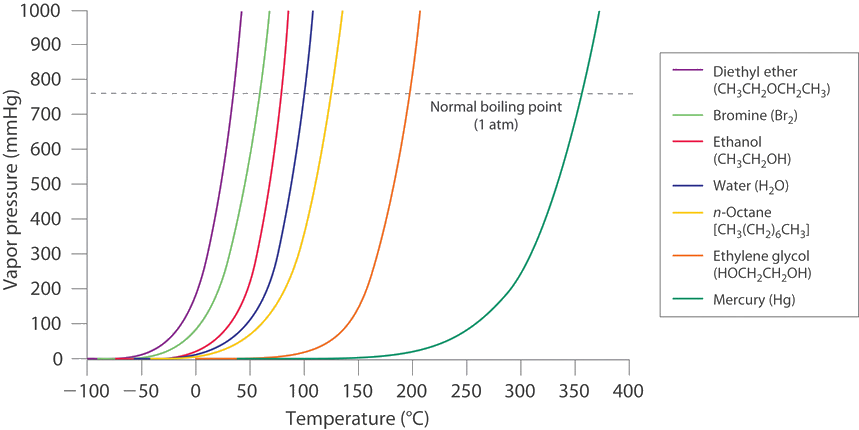
Un buen enfoque es encontrar un modelo matemático para el aumento de presión en función de la temperatura. Los experimentos mostraron que la presión de vapor\(P\) y la temperatura\(T\) están relacionadas,
\[P \propto \exp \left(- \dfrac{\Delta H_{vap}}{RT}\right) \ \label{1}\]
donde\(\Delta{H_{vap}}\) es la Entalpía (calor) de Vaporización y\(R\) es la constante de gas (8.3145 J mol -1 K -1).
Se puede encontrar una relación simple integrando la Ecuación\ ref {1} entre dos puntos finales de presión-temperatura:
\[\ln \left( \dfrac{P_1}{P_2} \right) = \dfrac{\Delta H_{vap}}{R} \left( \dfrac{1}{T_2}- \dfrac{1}{T_1} \right) \label{2}\]
donde\(P_1\) y\(P_2\) son las presiones de vapor a dos temperaturas\(T_1\) y\(T_2\). La ecuación\ ref {2} se conoce como la Ecuación Clausius-Clapeyron y nos permite estimar la presión de vapor a otra temperatura, si se conoce la presión de vapor a alguna temperatura, y si se conoce la entalpía de vaporización.
El orden de las temperaturas en la Ecuación\ ref {2} importa ya que la Ecuación Clausius-Clapeyron a veces se escribe con un signo negativo (y orden conmutado de temperaturas):
\[\ln \left( \dfrac{P_1}{P_2} \right) = - \dfrac{\Delta H_{vap}}{R} \left( \dfrac{1}{T_1}- \dfrac{1}{T_2} \right) \label{2B} \]
La presión de vapor del agua es de 1.0 atm a 373 K, y la entalpía de vaporización es de 40.7 kJ mol -1. Estimar la presión de vapor a temperatura 363 y 383 K respectivamente.
Solución
Usando la ecuación de Clausius-Clapeyron (Ecuación\(\ref{2B}\)), tenemos:
\[\begin{align} P_{363} &= 1.0 \exp \left[- \left(\dfrac{40,700}{8.3145}\right) \left(\dfrac{1}{363\;K} -\dfrac{1}{373\; K}\right) \right] \nonumber \\[4pt] &= 0.697\; atm \nonumber \end{align} \nonumber\]
\[\begin{align} P_{383} &= 1.0 \exp \left[- \left( \dfrac{40,700}{8.3145} \right)\left(\dfrac{1}{383\;K} - \dfrac{1}{373\;K} \right) \right] \nonumber \\[4pt] &= 1.409\; atm \nonumber \end{align} \nonumber\]
Obsérvese que el incremento en la presión de vapor de 363 K a 373 K es de 0.303 atm, pero el incremento de 373 a 383 K es de 0.409 atm. El incremento en la presión de vapor no es un proceso lineal.
Discusión
Podemos usar la ecuación Clausius-Clapeyron para construir toda la curva de vaporización. Existe una desviación del valor experimental, es decir, porque la entalpía de vaporización varía ligeramente con la temperatura.
La ecuación Clausius-Clapeyron también se puede aplicar a la sublimación; el siguiente ejemplo muestra su aplicación en la estimación del calor de sublimación.
Las presiones de vapor del hielo a 268 K y 273 K son 2.965 y 4.560 torr respectivamente. Estimar el calor de sublimación de hielo.
Solución
La entalpía de la sublimación es\(\Delta{H}_{sub}\). Usa una hoja de papel y deriva la ecuación Clausius-Clapeyron para que puedas obtener la forma:
\[\begin{align} \Delta H_{sub} &= \dfrac{ R \ln \left(\dfrac{P_{273}}{P_{268}}\right)}{\dfrac{1}{268 \;K} - \dfrac{1}{273\;K}} \nonumber \\[4pt] &= \dfrac{8.3145 \ln \left(\dfrac{4.560}{2.965} \right)}{ \dfrac{1}{268\;K} - \dfrac{1}{273\;K} } \nonumber \\[4pt] &= 52,370\; J\; mol^{-1}\nonumber \end{align} \nonumber\]
Obsérvese que el calor de sublimación es la suma del calor de fusión (6,006 J/mol a 0°C y 101 kPa) y el calor de vaporización (45,051 J/mol a 0 °C).
Mostrar que la presión de vapor del hielo a 274 K es mayor que la del agua a la misma temperatura. Obsérvese que la curva de vaporización también se llama la curva de vaporización.
Calcular\(\Delta{H_{vap}}\) para etanol, dada presión de vapor a 40 o C = 150 torr. El punto de ebullición normal para el etanol es de 78 o C.
Solución
Reconocer que tenemos DOS conjuntos de\((P,T)\) datos:
- Set 1: (150 torr a 40+273K)
- Set 2: (760 torr a 78+273K)
Luego usamos directamente estos datos en la Ecuación\ ref {2B}
\[\begin{align*} \ln \left(\dfrac{150}{760} \right) &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ \dfrac{1}{313} - \dfrac{1}{351}\right] \\[4pt] \ln 150 -\ln 760 &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ \dfrac{1}{313} - \dfrac{1}{351}\right] \\[4pt] -1.623 &= \dfrac{-\Delta{H_{vap}}}{8.314} \left[ 0.0032 - 0.0028 \right] \end{align*}\]
Luego resolviendo para\(\Delta{H_{vap}}\)
\[\begin{align*} \Delta{H_{vap}} &= 3.90 \times 10^4 \text{ joule/mole} \\[4pt] &= 39.0 \text{ kJ/mole} \end{align*} \]
Es importante no utilizar la ecuación Clausius-Clapeyron para la transición de sólido a líquido. Eso requiere el uso de la ecuación más general de Clapeyron
\[\dfrac{dP}{dT} = \dfrac{\Delta \bar{H}}{T \Delta \bar{V}} \nonumber\]
donde\(\Delta \bar{H}\) y\(\Delta \bar{V}\) es el cambio molar en la entalpía (la entalpía de fusión en este caso) y el volumen respectivamente entre las dos fases en la transición.


http://www.kayelaby.npl.co.uk/chemis...3_4/3_4_1.html