24.6: Presiones de Vapor de Soluciones Binarias Volátiles

Última actualización
Guardar como PDF

Page ID: 79319

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Los comportamientos de soluciones ideales de compuestos volátiles siguen la Ley de Raoult. La Ley de Henry se puede utilizar para describir las desviaciones de la idealidad. La ley de Henry establece:

\[ P_B = k_H P_B^o\]

Para lo cual se determina la constante de la Ley de Henry (\(k_H\)) para el compuesto específico. La Ley de Henry se utiliza a menudo para describir las solubilidades de los gases en los líquidos. La relación con la Ley de Raoult se resume en la Figura\(\PageIndex{1}\).

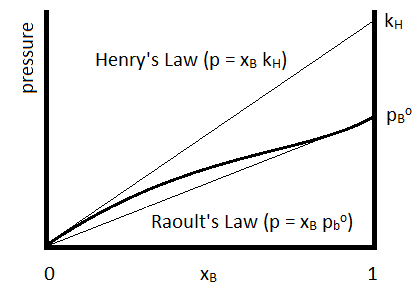
Figura\(\PageIndex{1}\): La relación entre la Ley de Raoult y la Ley de Henry para una mezcla binaria.

La Ley de Henry está representada por la línea recta superior y la Ley de Raoult por la inferior.

Ejemplo\(\PageIndex{1}\): Solubility of Carbon Dioxide in Water

La solubilidad de\(CO_2(g)\) en agua a 25 ^o C es de 3.32 x 10 ^-2 M con una presión parcial de\(CO_2\) sobre la solución de 1 bar. Suponiendo que la densidad de una solución saturada sea de 1 Kg/L, calcule la constante de la Ley de Henry para\(CO_2\).

Solución:

En un L de solución, hay 1000 g de agua (suponiendo que la masa de CO ₂ disuelta sea despreciable).

\[ (1000 \,g) \left( \dfrac{1\, mol}{18.02\,g} \right) = 55\, mol\, H_2O\]

La solubilidad de se\(CO_2\) puede utilizar para encontrar el número de moles de\(CO_2\) disuelto en 1 L de solución también:

\[ \dfrac{3.32 \times 10^{-2} mol}{L} \cdot 1 \,L = 3.32 \times 10^{-2} mol\, CO_2\]

y así la fracción molar de\(CO_2\) es

\[ \chi_b = \dfrac{3.32 \times 10^{-2} mol}{55.5 \, mol} = 5.98 \times 10^{-4}\]

Y así

\[10^5\, Pa = 5.98 \times 10^{-4} k_H\]

\[ k_H = 1.67 \times 10^9\, Pa\]

Azeótropos

Un azeótropo se define como la composición común de vapor y líquido cuando tienen la misma composición.

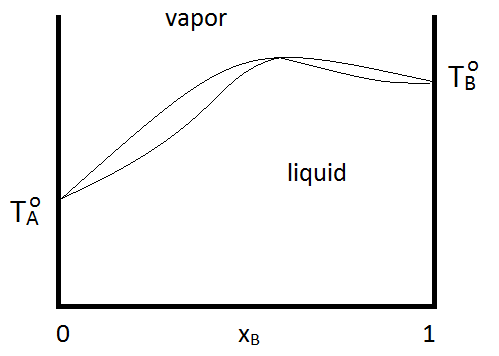
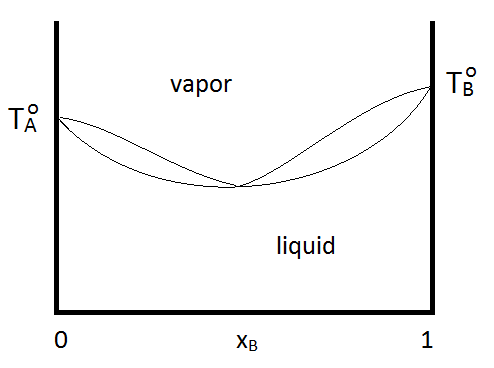
Figura\(\PageIndex{2}\): Diagramas de fase para (izquierda) un azeótropo de punto de ebullición máximo y (derecha) azeótropo de punto de ebullición máximo Ta.

Los azeótropos pueden ser de ebullición máxima o mínima ebullición, como se muestra en la Figura\(\PageIndex{2; left}\). Independientemente, la destilación no puede purificarse más allá del punto azeotrópico, ya que las fases vapor y líquida tienen la misma composición. Si un sistema forma un azeótropo de ebullición mínima y tiene un rango de composiciones y temperaturas a las que existen dos fases líquidas, el diagrama de fases podría verse como Figura\(\PageIndex{2; right}\):

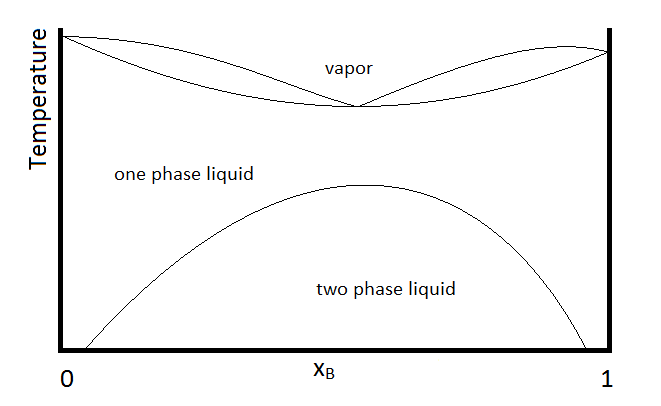
Figura\(\PageIndex{3}\): *Diagrama de fases para una solución binaria con el punto de ebullición de un azeótropo mínimo de ebullición que es mayor que cuando los componentes son miscibles (monofásico).*

Otra posibilidad que es común es que dos sustancias formen un líquido bifásico, formen un azeótropo mínimo de ebullición, pero que el azeótropo hierva a una temperatura por debajo de la cual las dos fases líquidas se vuelven miscibles. En este caso, el diagrama de fases se verá como Figura\(\PageIndex{3}\).

Ejemplo\(\PageIndex{1}\):

En el diagrama, la conformación de un sistema en cada región se resume debajo del diagrama. El punto e indica la composición azeotrópica y la temperatura de ebullición.

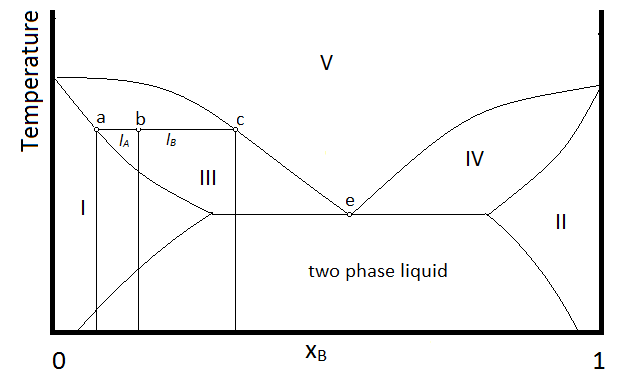
Líquido monofásico (principalmente compuesto A)
Líquido monofásico (principalmente compuesto B)
Líquido monofásico (principalmente A) y vapor
Líquido monofásico (principalmente B) y vapor
Vapor (miscible en todas las fracciones molares ya que es un gas)

Solución

Dentro de cada región bifásica (III, IV y la región líquida bifásica, se aplicará la regla de palanca para describir la composición de cada fase presente. Así, por ejemplo, el sistema con la composición y la temperatura representadas por el punto b (un líquido monofásico que en su mayoría es el compuesto A, designado por la composición en el punto a, y vapor con una composición designada por la del punto c), será descrito por la regla de palanca usando las longitudes de las líneas de unión l _A y l _B.

La ley de Gibbs-Duhem y Henry

¿Qué sucede cuando Raoult no se sostiene en toda la gama? Recordemos que en un gas:

\[μ_j = μ_j^o + RT \ln \dfrac{P_j}{P^o} \label{B} \]

\[μ_j = μ_j^o + RT \ln P_j \nonumber \]

después de\(P^o=1\; bar\) abandonar la notación. Obsérvese que numéricamente esto no importa, ya que ahora\(P_j\) se asume que es adimensional.

Consideremos\(dμ_1\) a temperatura constante:

\[dμ_1 = RT\left(\dfrac{\partial \ln P_1}{ \partial x_1}\right)dx_1 \nonumber \]

así mismo:

\[dμ_2 = RT\left(\dfrac{\partial \ln P_2}{ \partial x_2}\right)dx_2 \nonumber \]

Si sustituimos en la expresión de Gibbs-Duhem obtenemos:

\[x_1 \left(\dfrac{∂\ln P_1}{ ∂x_1}\right) dx_1+x_2 \left(\dfrac{∂\ln P_2}{∂x_2} \right) dx_2=0 \nonumber \]

Porque\(dx_1= -dx_2\):

\[x_ 1 \left( \dfrac{∂\ln P_1}{ ∂x_1} \right) =x_2 \left( \dfrac{∂\ln P_2}{∂x_2} \right) \nonumber \]

(Esta es una forma alternativa de escribir Gibbs-Duhem).

Si en el límite para\(x_1 \rightarrow 1\) Raoult Law sostiene entonces

\[P_1 \rightarrow x_1P^*_1 \nonumber \]

Así:

\[ \dfrac{∂ \ln P_1}{∂x_1} = \dfrac{1}{x_1} \nonumber \]

\[\dfrac{x_1}{x_1}=x_2 \dfrac{∂ \ln P_2}{∂x_2} \nonumber \]

\[1=x_2 \dfrac{∂ \ln P_2}{ ∂x_2} \nonumber \]

\[\dfrac{1}{x_2}= \dfrac{∂ \ln P_2}{∂x_2} \label{EqA12} \]

Podemos integrar Ecuación\(\ref{EqA12}\) para formar una impresión logarítmica, pero tendrá una constante de integración:

\[\ln P_2 =\ln x_2 + constant \nonumber \]

Esta constante de integración se puede plegar en el logaritmo como una constante multiplicativa,\(K\)

\[\ln P_2 = \ln \left(K x_2 \right) \nonumber \]

Entonces para\(x_1 \rightarrow 1\) (es decir,\(x_2 \rightarrow 0\)), obtenemos eso

\[P_2=K x_2 \nonumber \]

donde\(K\) hay alguna constante, pero no necesariamente\(P^*\). Lo que esto demuestra es que cuando un componente sigue a Raoult el otro debe seguir a Henry y viceversa. (Tenga en cuenta que el caso ideal es un subconjunto de este caso, en que el valor de\(K\) entonces se convierte\(P^*\) y la linealidad debe mantenerse en todo el rango.)

Funciones Margules

Por supuesto, un gran inconveniente de la ley Henry es que solo describe lo que sucede en los dos extremos del diagrama de fases y no en el medio. En casos de no idealidad moderada, es posible describir todo el rango (al menos en buena aproximación) usando una función Margules:

\[P_1= \left(x_1P^*_1 \right)f_{Mar} \nonumber \]

La función\(f_{Mar}\) tiene la forma:

\[f_{Mar}= \text{exp} \left[ αx_2^2+βx_2^3+δx_2^3 + .... \right] \nonumber \]

Observe que la función Margules involucra la fracción molar del componente opuesto. Es un exponencial con una expansión en serie. con el término constante y lineal faltante. Como puede ver la función tiene una serie de parámetros\(α\),\(β\),\(δ\) etc. que necesitan ser determinados por experimento. En general, cuanto más diverja el sistema de la idealidad, más parámetros necesitará. Usando Gibbs-Duhem es posible traducir la expresión para\(P_1\) en la correspondiente para\(P_2\).