27.3: La distribución de velocidades moleculares viene dada por la distribución Maxwell-Boltzmann

La distribución de Boltzmann

Si tuviéramos que trazar el número de moléculas cuyas velocidades caen dentro de una serie de rangos estrechos, obtendríamos una curva ligeramente asimétrica conocida como distribución de velocidad. El pico de esta curva correspondería a la velocidad más probable. Esta curva de distribución de velocidad se conoce como la distribución de Maxwell-Boltzmann, pero con frecuencia es referida solo por el nombre de Boltzmann. La ley de distribución Maxwell-Boltzmann fue elaborada por primera vez alrededor de 1860 por el gran físico escocés, James Clerk Maxwell (1831-1879), quien es mejor conocido por descubrir las leyes de la radiación electromagnética. Posteriormente, el físico austriaco Ludwig Boltzmann (1844-1906) puso la relación sobre una base teórica más sólida y simplificó un poco las matemáticas. Boltzmann fue pionero en la aplicación de la estadística a la física y termodinámica de la materia y fue un ferviente partidario de la teoría atómica de la materia en un momento en que todavía no era aceptada por muchos de sus contemporáneos.

Figura 27.3.1 : Maxwell (izquierda) y Boltzmann (derecha) son los encargados de describir la distribución de velocidad de las moléculas de gas

En la sección 27.2 vimos que la función de distribución para las velocidades moleculares en la dirección x viene dada por:

\[f(v_x) = \underbrace{\sqrt{ \dfrac{m}{2\pi k_BT} }}_{\text{normalization term}} \underbrace{\exp \left(\dfrac{-mv_x^2}{2k_BT} \right)}_{\text{exponential term}} \nonumber \]

Sin embargo, las muestras de gas reales tienen moléculas no solo con una distribución de velocidades moleculares y también una distribución aleatoria de direcciones. Usando propiedades de magnitud vectorial normal (o simplemente usando el Teorema de Pitágoras), se puede ver que

\[ \langle v \rangle^2 = \langle v_x \rangle^2 + \langle v_y \rangle^2 + \langle v_z \rangle^2 \nonumber \]

Dado que la dirección de desplazamiento es aleatoria, la velocidad puede tener cualquier componente en las direcciones x, y o z con igual probabilidad. Como tal, el valor promedio de los componentes x, y o z de velocidad debe ser el mismo. Y así

\[ \langle v \rangle^2 = 3 \langle v_x \rangle^2 \nonumber \]

Sustituyendo esto en la expresión para rendimientos de presión

\[ p =\dfrac{ N_{tot}m}{3V} \langle v \rangle^2 \nonumber \]

Todo lo que queda es determinar la forma de distribución de las magnitudes de velocidad que pueden tomar las moléculas de gas. En su artículo de 1860 (Ilustraciones de la teoría dinámica de los gases. Parte 1. Sobre los movimientos y colisiones de esferas perfectamente elásticas, 1860), Maxwell propuso una forma para esta distribución de velocidades que demostró ser consistente con las propiedades observadas de los gases (como sus viscosidades). Derivó esta expresión a partir de una transformación del sistema de coordenadas de coordenadas cartesianas (\(x\),\(y\),\(z\)) a coordenadas polares esféricas (\(v\),\(\theta\),\(\phi\)). En este nuevo sistema de coordenadas,\(v\) representa la magnitud de la velocidad (o la velocidad) y todos los datos direccionales se transportan en los ángulos\(\theta\) y\(\phi\). La unidad de volumen infinitesimal se convierte

\[ dx\,dy\,dz\, = v^2 \sin( \theta) \,dv\,d\theta \,d\phi \nonumber \]

Aplicando esta transformación de coordenadas La distribución de Maxwell tomó la siguiente forma

\[f(v) = 4\pi v^2 \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \label{27.3.1} \]

La distribución de la velocidad en todas las direcciones

La distribución de la energía cinética en tres dimensiones

Como se señaló anteriormente, la función de distribución de las energías moleculares para una dimensión es

\[f(v_x) = \sqrt{ \dfrac{m}{2\pi k_BT} } \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) \nonumber \]

Para obtener una distribución de probabilidad tridimensional, se multiplica la función de distribución para cada una de las tres dimensiones de manera que

\[f(v_x, v_y, v_z) = \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \nonumber \]

dado\[ \langle v \rangle^2 = \langle v_x \rangle^2 + \langle v_y \rangle^2 + \langle v_z \rangle^2 \nonumber \]

La conversión de la distribución de energía a la distribución de velocidad

Para convertir la distribución de energía tridimensional en una distribución de velocidad en todo el espacio, la distribución de energía debe sumarse en todas las direcciones. Esta suma se suele describir imaginando un “espacio de velocidad” en coordenadas polares esféricas. Como se señaló anteriormente, en este nuevo sistema de coordenadas,\(v\) representa la magnitud de la velocidad (o la velocidad) y todos los datos direccionales se transportan en los ángulos\(\theta\) y\(\phi\). La unidad de volumen infinitesimal se convierte

\[ dx\,dy\,dz\, = v^2 \sin( \theta) \,dv\,d\theta \,d\phi \nonumber \]

Te integras sobre\(\theta\) y\(\phi\) para sumar sobre todo el espacio, así

\[f(v) = \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \underbrace {\int_0^{\pi} \int_0^{2\pi} v^2 \sin \theta d \phi d \theta}_{=4\pi v^2} \nonumber \]

Esta ecuación se reordena para dar

\[f(v) = 4\pi v^2 \left(\dfrac{m}{2\pi k_BT} \right)^{3/2} \exp \left(\dfrac{-mv^2}{2k_BT} \right) \nonumber \]

Se puede pensar que esta función tiene tres partes básicas: una constante de normalización (\(N\)), una dependencia de la velocidad (\(v^2\)) y un término exponencial que contiene la energía cinética (\(½ mv^2\)).

Debido a que la función representa la fracción de moléculas con la velocidad\(v\), la suma de las fracciones para todas las velocidades posibles debe ser unidad. Esta suma se puede calcular como una integral. La constante de normalización asegura que

\[ \int_0^{\infty} f(v) dv = 1 \nonumber \]

Así, la constante de normalización es

\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \nonumber \]

Las distribuciones de velocidad dependen de la temperatura y la masa

Las temperaturas más altas permiten que una mayor fracción de moléculas adquieran mayores cantidades de energía cinética, lo que provoca que las parcelas de Boltzmann se extiendan. La Figura 27.3.2 muestra cómo la distribución Maxwell-Boltzmann se ve afectada por la temperatura. A temperaturas más bajas, las moléculas tienen menos energía. Por lo tanto, las velocidades de las moléculas son menores y la distribución tiene un rango menor. A medida que aumenta la temperatura de las moléculas, la distribución se aplana. Debido a que las moléculas tienen mayor energía a mayor temperatura, las moléculas se mueven más rápido.

Observe cómo los extremos izquierdos de las parcelas están anclados a velocidad cero (siempre habrá algunas moléculas que pasan a estar en reposo). Como consecuencia, las curvas se aplanan a medida que las temperaturas más altas hacen que los estados de movimiento adicionales de mayor velocidad sean más accesibles. El área debajo de cada parcela es la misma para un número constante de moléculas.

Figura 27.3.2: Distribución Maxwell de velocidades para moléculas de hidrógeno a diferentes temperaturas.

Cálculo de la Velocidad Media

Usando la distribución Maxwell como distribución de probabilidades, se puede determinar la velocidad molecular promedio en una muestra de moléculas de gas.

\[ \begin{align} \langle v \rangle & = \int _{-\infty}^{\infty} v \,f(v) dv \nonumber \\ & = \int _{-\infty}^{\infty} v\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^3 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \end{align} \nonumber \]

Lo siguiente se puede encontrar en una tabla de integrales:

\[ \int_0^{\infty} x^{2n+1} e^{-ax^2} dx = \dfrac{n!}{2a^{n+1}} \nonumber \]

Entonces

\[\langle v \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1}{2 \left( \dfrac{m}{2 k_B T} \right) ^2 } \right] \nonumber \]

Lo que simplifica

\[\langle v \rangle = \left( \dfrac{8 k_BT}{\pi m} \right) ^{1/2} \nonumber \]

Nota: ¡el valor de\(\langle v \rangle \) es el doble del\(\langle v_x \rangle \) que se derivó en un ejemplo anterior!

\[\langle v \rangle = 2\langle v_x \rangle \nonumber \]

Ejemplo 27.3.1 :

¿Cuál es el valor promedio de la velocidad al cuadrado según la ley de distribución Maxwell?

Solución:

\[ \begin{align} \langle v^2 \rangle & = \int _{-\infty}^{\infty} v^2 \,f(v) dv \nonumber \\ & = \int _{-\infty}^{\infty} v^2\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^4 \text{exp} \left( \dfrac{-m v^2}{2 k_BT} \right)\ dv \nonumber \end{align} \nonumber \]

Una tabla de integrales indica que

\[ \int_0^{\infty} x^{2n} e^{-ax^2} dx = \dfrac{1 \cdot 3 \,cdot 5 \dots (2n-1)}{2^{n+1}a^n} \sqrt{\dfrac{\pi}{a}} \nonumber \]

Sustitución (señalando que\(n = 2\)) rinde

\[\langle v^2 \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1 \cdot 3}{2^3 \left( \dfrac{m}{2 k_BT} \right) ^2 } \sqrt{\dfrac{\pi}{\left( \dfrac{m}{2 k_BT} \right)}} \right] \nonumber \]

lo que simplifica

\[\langle v^2 \rangle = \dfrac{3 k_BT}{ m} \nonumber \]

Nota: La raíz cuadrada de esta velocidad cuadrada promedio se denomina velocidad media cuadrática (RMS) y tiene el valor

\[v_{rms} = \sqrt{ \langle v^2 \rangle } = \left( \dfrac{3 k_BT}{ m} \right)^{1/2} \nonumber \]

Todas las moléculas tienen la misma energía cinética (\(½ mv^2\)) a la misma temperatura, por lo que la fracción de moléculas con mayores velocidades aumentará a medida que m, y así el peso molecular, disminuya. La Figura 27.3.3 muestra la dependencia de la distribución de Maxwell-Boltzmann de la masa molecular. En promedio, las moléculas más pesadas se mueven más lentamente que las moléculas más ligeras. Por lo tanto, las moléculas más pesadas tendrán una distribución de velocidad menor, mientras que las moléculas más ligeras tendrán una distribución de velocidad que está más extendida.

Figura 27.3.3: Distribución Maxwell de velocidades a 800 K para diferentes gases de diferentes masas moleculares.

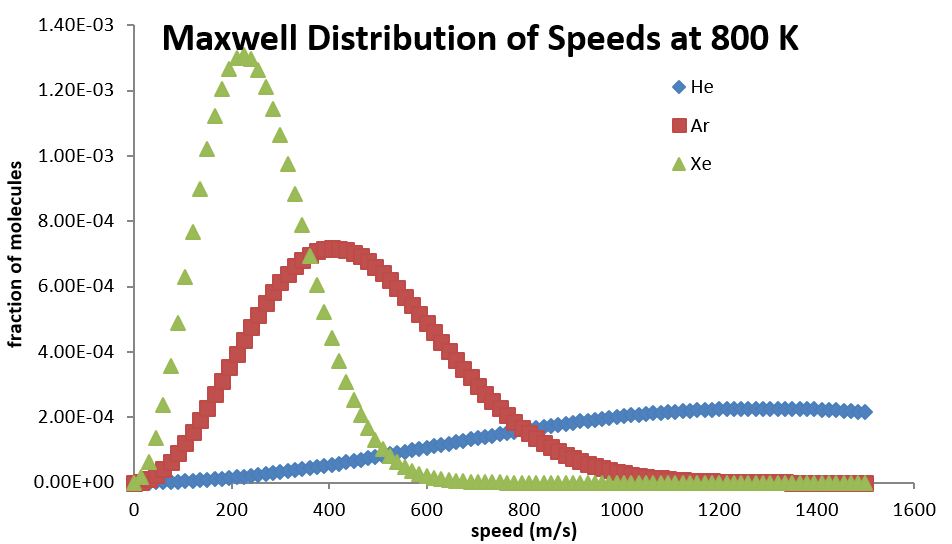
Expresiones de velocidad relacionadas

Por lo general, estamos más interesados en las velocidades de las moléculas que en sus velocidades componentes. La distribución Maxwell—Boltzmann para la velocidad sigue inmediatamente de la distribución del vector de velocidad, arriba. Tenga en cuenta que la velocidad de una partícula de gas individual es:

\[v =\sqrt{v_x^2+ v_y^2 = v_z^2} \nonumber \]

De la distribución Maxwell-Boltzmann se pueden derivar tres expresiones de velocidad:

• la velocidad más probable,
• la velocidad media, y
• la velocidad cuadrática media.

La velocidad más probable es el valor máximo en la gráfica de distribución (Figura 27.3.4 ). Esto se establece al encontrar la velocidad cuando la derivada de la Ecuación\(\ref{27.3.1}\) es cero

\[\dfrac{df(v)}{dv} = 0 \nonumber \]

que es

\[\color{red} v_{mp}=\sqrt {\dfrac {2RT}{M}} \label{3a} \]

Figura 27.3.4 : La distribución Maxwell-Boltzmann se desplaza a velocidades más altas y se amplía a temperaturas más altas. de OpenStax. La velocidad en la parte superior de la curva se llama la velocidad más probable porque el mayor número de moléculas tiene esa velocidad.

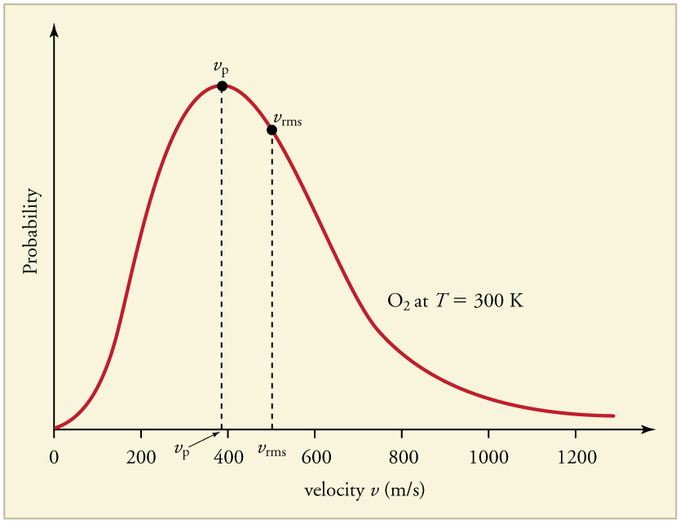
La velocidad promedio es la suma de las velocidades de todas las moléculas dividida por el número de moléculas.

\[\color{red} v_{avg}= \bar{v} = \int_0^{\infty} v f(v) dv = \sqrt {\dfrac{8RT}{\pi M}} \nonumber \]

La velocidad media cuadrada de la raíz es la raíz cuadrada de la velocidad promedio al cuadrado.

\[ \color{red} v_{rms}= \bar{v^2} = \sqrt {\dfrac {3RT}{M}} \nonumber \]

donde

• \(R\)es la constante del gas,
• \(T\)es la temperatura absoluta y
• \(M\)es la masa molar del gas.

Siempre se deduce que para los gases que siguen la distribución de Maxwell-Boltzmann:

\[v_{mp}< v_{avg}< v_{rms} \nonumber \]

Problemas

1. Utilizando la función Maxwell-Boltzman, se calcula la fracción de moléculas de gas argón con una velocidad de 305 m/s a 500 K.
2. Si el sistema en problema 1 tiene 0.46 moles de gas argón, ¿cuántas moléculas tienen la velocidad de 305 m/s?
3. Calcular los valores de\(C_{mp}\),\(C_{avg}\), y\(C_{rms}\) para el gas xenón a 298 K.
4. A partir de los valores calculados anteriormente, etiquetar la parcela de distribución de Boltzmann con las ubicaciones aproximadas de (C_ {mp}\)\(C_{avg}\), y\(C_{rms}\).
5. ¿Qué tendrá una distribución de velocidad mayor, helio a 500 K o argón a 300 K? ¿Helio a 300 K o argón a 500 K? ¿Argón a 400 K o argón a 1000 K?

RESPUESTAS

1. 0.00141
2. \(3.92 \times 10^{20}\)moléculas de argón
3. c _mp = 194.27 m/s, c _avg = 219.21 m/s, c _rms = 237.93 m/s
4. Como se indicó anteriormente, C _mp es la velocidad más probable, por lo que estará en la parte superior de la curva de distribución. A la derecha de la velocidad más probable estará la velocidad media, seguida de la velocidad media cuadrática.
5. Pista: Utilice las expresiones de velocidad relacionadas para determinar la distribución de las moléculas de gas: helio a 500 K. helio a 300 K. argón a 1000 K.

Fuentes

1. Dunbar, R.C. Derivando el Maxwell Distribution J. Chem. Ed. 1982, 59, 22-23.
2. Peckham, G.D.; McNaught, I.J.; Aplicaciones de la distribución Maxwell-Boltzmann J. Chem. Ed. 1992, 69, 554-558.
3. Chang, R. Química Física para las Biociencias, 25-27.
4. Hiperfísica: http://hyperphysics.phy-astr.gsu.edu...maxspe.html#c3

Colaboradores y Atribuciones

• Prof. David Blauch (Davidson College)

• Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

• Adam Maley (Hope College)

• Patrick E. Fleming (Department of Chemistry and Biochemistry; California State University, East Bay)

• Stephanie Schaertel (Grand Valley State University)
• Tom Neils (Grand Rapids Community College, editing)