32.1: Números complejos

Números Reales

Pensemos en los números ordinarios como establecidos en una línea que va al infinito tanto en dirección positiva como negativa. Podríamos comenzar tomando un tramo de la línea cerca del origen (es decir, el punto que representa el número cero) y poniendo los enteros de la siguiente manera:

A continuación, podríamos sumar en números racionales, como ½, 23/11, etc., luego los irracionales como\(\sqrt{2}\), luego números como\(\pi\), y así sucesivamente, así que cualquier número que se te ocurra tiene su lugar en esta línea. Ahora tomemos un punto de vista ligeramente diferente, y pensemos en los números representados por un vector desde el origen hasta ese número, entonces 1 es

y, por ejemplo, —2 está representado por:

Tenga en cuenta que si un número se multiplica por —1, el vector correspondiente se gira 180 grados. En imágenes,

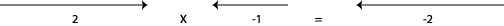
El “vector” 2 se gira\(\pi\), o 180 grados, cuando se multiplica por —1.

Ejemplo A.1

¿Cuáles son las raíces cuadradas de 4?

Solución

Bueno, 2, obviamente, pero también —2, porque multiplicar el vector que apunta hacia atrás —2 por —2 no sólo duplica su longitud, sino que también lo gira 180 grados, por lo que ahora está apuntando en la dirección positiva. Parece que hemos inventado una manera dura de afirmar que multiplicar dos negativos da un positivo, pero pensar en términos de convertir vectores por 180 grados dará sus frutos pronto.

Resolviendo ecuaciones cuadráticas

Al resolver la ecuación cuadrática estándar

\[ax^2 + bx + c = 0 \label{A.1} \]

encontramos que la solución es:

\[ x =\dfrac{-b \pm \sqrt{b^2-ac}}{2a} \label{A.2} \]

El problema con esto es que a veces la expresión dentro de la raíz cuadrada es negativa. ¿Qué significa eso? Para algunos problemas en física, significa que no hay solución. Por ejemplo, si lanzo una pelota directamente hacia arriba a 10 metros por segundo, y pregunto cuándo alcanzará una altura de 20 metros, tomando g = 10 m por segundo ², la solución de la ecuación cuadrática para el tiempo t tiene un número negativo dentro de la raíz cuadrada, y eso significa que el pelota no llega a los 20 metros, así que la pregunta realmente no tenía sentido.

Encontraremos, sin embargo, que existen otros problemas, en amplias áreas de la física, donde los números negativos dentro de las raíces cuadradas tienen una significación física importante. Por esa razón, necesitamos idear un esquema para interpretarlos.

La ecuación cuadrática más simple que da problemas es:

\[x^2 + 1 = 0 \label{A.3} \]

siendo las soluciones

\[x = \pm \sqrt{-1}\label{A.4} \]

¿Qué significa eso? Acabamos de ver que el cuadrado de un número positivo es positivo, y el cuadrado de un número negativo también es positivo, ya que multiplicar un número negativo, que apunta hacia atrás, por otro, que convierte cualquier vector en 180 grados, da un vector positivo. Otra forma de decir lo mismo es considerar el signo menos en sí, -, como un operador que gira el número al que se aplica a través de 180 grados. Ahora\((-2)\times (-2)\) tiene dos rotaciones de este tipo en ella, dando los 360 grados completos de nuevo al eje positivo.

Para darle sentido a la raíz cuadrada de un número negativo, necesitamos encontrar algo que al multiplicarse por sí mismo dé un número negativo. Concentrémonos por el momento en la raíz cuadrada de —1, de la ecuación cuadrática anterior. Piense en —1 como el operador — actuando sobre el vector 1, entonces el — gira el vector 180 grados. Necesitamos encontrar la raíz cuadrada de este operador, el operador que aplicó dos veces da la rotación a través de 180 grados. Dicho así, es bastante obvio que el operador que queremos gira el vector 1 a través de 90 grados.

Pero si tomamos un número positivo, como 1, y giramos su vector solo 90 grados, no es un número en absoluto, al menos en nuestro sentido original, ya que ponemos todos los números conocidos en una línea, y ahora hemos girado 1 lejos de esa línea. El nuevo número creado de esta manera se llama un número imaginario puro, y se denota por\(i\).

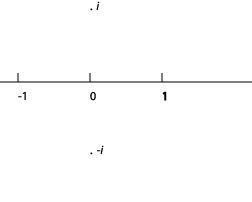
Una vez que hayamos encontrado la raíz cuadrada de —1, podemos usarla para escribir la raíz cuadrada de cualquier otro número negativo—por ejemplo,\(2i\) es la raíz cuadrada de\(–4\). Armando un número real de la línea original con un número imaginario (un múltiplo de i) da un número complejo. Evidentemente, los números complejos llenan todo el plano bidimensional. Tomando coordenadas cartesianas ordinarias, cualquier punto\(P\) del plano puede escribirse como\((x, y)\) donde se alcanza el punto desde el origen yendo\(x\) unidades en la dirección del eje real positivo, luego y unidades en la dirección definida por\(i\), en otras palabras, el \(y\) eje.

Así, el punto P con coordenadas (x, y) se puede identificar con el número complejo z, donde

\[z = x + iy. \label{A.5} \]

El plano a menudo se llama el plano complejo, y representar números complejos de esta manera a veces se conoce como un diagrama de Argand.

Visualizando los números complejos como vectores bidimensionales, es claro cómo sumar dos de ellos juntos. Si z ₁ = x ₁ + iy ₁, y z ₂ = x ₂ + iy ₂, entonces z ₁ + z ₂ = (x ₁ + x ₂) + i (y ₁ + y ₂). Las partes reales y las partes imaginarias se agregan por separado, al igual que los componentes vectoriales.

Multiplicar dos números complejos juntos no tiene una interpretación tan simple. Sin embargo, es bastante sencillo: se aplican reglas algebraicas ordinarias, con i ² reemplazado donde aparece por - 1. Entonces, por ejemplo, para multiplicar z ₁ = x ₁ + iy ₁ por z ₂ = x ₂ + iy ₂,

\[z_1z_2 = (x_1 + iy_1)( x_2 + iy_2) = (x_1x_2 - y_1y_2) + i(x_1y_2 + x_2y_1). \label{A.6} \]

Coordenadas polares

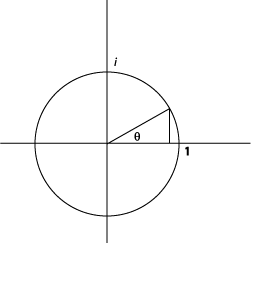
Algunas propiedades de los números complejos se entienden más fácilmente si se representan usando las coordenadas polares\(r, \theta\) en lugar de\((x, y)\) ubicarlas\(z\) en el plano complejo.

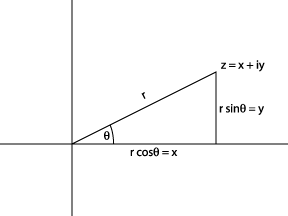
Tenga en cuenta que se\(z = x + iy\) puede escribir\(r(\cos \theta + i \sin \theta)\) a partir del diagrama anterior. De hecho, esta representación conduce a una imagen más clara de la multiplicación de dos números complejos:

\[\begin{align} z_1z_2 &= r_2 ( \cos(\theta_1 + i\sin \theta_1) r_2( \cos(\theta_2 + i\sin \theta_2) \label{A.7} \\[4pt] & = r_1r_2 \left[ (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + i (\sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2) \right] \label{A.8} \\[4pt] & = r_1r_2 \left[ \cos(\theta_1+\theta_2) + i\sin (\theta_1+\theta_2) \right] \label{A.9} \end{align} \]

Entonces, si

\[ z = r(cos \theta + i\sin \theta ) = z_1z_2 \label{A.10} \]

entonces

\[r = r_1r_2 \label{A.11} \]

y

\[\theta=\theta_1\theta_2 \label{A.12} \]

Es decir, para multiplicar juntos dos números complejos, multiplicamos las r —llamadas los módulos — y sumamos las fases, los s. el\(\theta\) módulo a menudo\(r\) se denota por\(|z|\), y se llama mod z, la fase \(\theta\)a veces se conoce como arg z. Por ejemplo,\(|i| = 1\),\(\text{arg}\; i = \pi/2\).

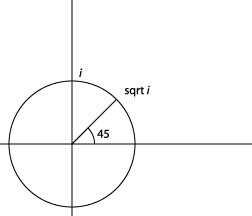
Ahora podemos ver que, aunque tuvimos que introducir estos números complejos para tener una\(\sqrt{-1}\), no necesitamos traer nuevos tipos de números para obtener\(\sqrt{-1}\), o\(\sqrt{i}\). Claramente,\(|\sqrt{i}|=1\),\( arg \sqrt{i} = 45°\). Está en el círculo de radio unitario centrado en el origen, a 45 °, y al cuadrarlo solo duplica el ángulo.

El círculo de unidades

De hecho, este círculo —llamado círculo unitario — juega un papel importante en la teoría de los números complejos y cada punto del círculo tiene la forma

\[ z = \cos \theta + i \sin \theta = Cis(\theta) \label{A.13} \]

Dado que todos los puntos del círculo unitario tienen\(|z| = 1\), por definición, multiplicar dos cualesquiera de ellos juntos solo equivale a sumar los ángulos, por lo que nuestra nueva función\(Cis(\theta)\) satisface

\[ Cis(\theta_1)Cis(\theta_2)=Cis(\theta_1+\theta_2). \label{A.14} \]

¡Pero así es como funciona la multiplicación para los exponentes! Es decir,

\[a^{\theta_1}a^{\theta_2} = a^{\theta_1+\theta_2} \label{A.15} \]

para\(a\) cualquier constante, lo que sugiere fuertemente que tal vez nuestra función no\(Cis(\theta\) sea más que alguna constante\(a\) elevada al poder\(\theta\), es decir,

\[ Cis(\theta) = a^{\theta}\label{A.16} \]

Resulta conveniente escribir\(a^{\theta} = e^{(\ln a)\theta} = e^{A \theta}\), dónde\(A = \ln a\). Esta línea de razonamiento nos lleva a escribir

\[\cos \theta + i\sin \theta = e^{A\theta} \label{A.17} \]

Ahora bien, para que la “fórmula de suma” anterior funcione para la multiplicación,\(A\) debe ser una constante, independiente de\(\theta\). Por lo tanto, podemos encontrar el valor de A eligiendo\(\theta\) para qué cosas son simples. Tomamos\(\theta\) para ser muy pequeños, en este límite:

\[ \cos \theta = 1 \nonumber \]

\[ \sin \theta = \theta \nonumber \]

\[ e^{A\theta} = 1+ A\theta \nonumber \]

con bajamos términos de orden\(\theta^2\) y superiores.

Sustituyendo estos valores en la Ecuación\ ref {A.17} da\(\theta\)

Entonces encontramos:

\[ (\cos \theta + i \sin \theta) e ^{i \theta} \label{A.18} \]

Para probar este resultado, ampliamos\(e^{i \theta}\):

\[ \begin{align} e^{i \theta} &= 1 + i\theta + \dfrac{(i\theta)^2}{2!} + \dfrac{(i\theta)^3}{3!} + \dfrac{(i\theta)^4}{4!} + \dfrac{(i\theta)^5}{5!} ... \label{A.19a} \\[4pt] &= 1 + i\theta - \dfrac{\theta^2}{2!} - \dfrac{i\theta^3}{3!} +\dfrac{\theta^4}{4!} +\dfrac{i\theta^5}{5!} ... \label{A.19b} \\[4pt] &= \left( 1 - \dfrac{\theta^2}{2!} + \dfrac{\theta^4}{4!} \right) + i \left(\theta - \dfrac{i\theta^3}{3!}+\dfrac{i\theta^5}{5!} \right) \label{A.19c} \\[4pt] &= \cos \theta + i\sin \theta \label{A.19d} \end{align} \]

Escribimos\(= \cos \theta + i\sin \theta\) en Ecuación\ ref {a.19d} porque las series entre paréntesis son precisamente las series de Taylor para\(\cos \theta\) y\(\sin \theta\) confirmando nuestra ecuación para\(e^{i\theta}\). Cambiar el signo de\(\theta\) ello es fácil ver que

\[ e^{-i \theta} = \cos \theta - i\sin \theta \label{A.20} \]

por lo que las dos funciones trigonométricas se pueden expresar en términos de exponenciales de números complejos:

\[\cos (\theta) = \dfrac{1}{2} \left( e^{i\theta} + e^{-i \theta} \right) \nonumber \]

\[\sin (\theta) = \dfrac{1}{2i} \left( e^{i\theta} - e^{-i \theta} \right) \nonumber \]

Fórmula Euler

La fórmula de Euler establece que cualquier número complejo puede escribirse:

\[e^{i \theta} = \cos \theta + i\sin \theta \nonumber \]

Colaboradores y Atribuciones

• Michael Fowler (Beams Professor, Department of Physics, University of Virginia)