2.2: Bandas de Orbitales en Sólidos

El modelo de partículas en caja no solo ofrece una representación conceptual útil de los electrones que se mueven en polienos, sino que también es el modelo de orden cero de estructuras de banda en sólidos. Consideremos un simple cristal unidimensional que consiste en un gran número de átomos o moléculas, cada uno con un solo orbital (las esferas azules que se muestran a continuación) que contribuye a la unión. Arreglemos estos bloques de construcción en una celosía regular como se muestra en la Figura 2.5.

Figura 2.5. Los niveles de energía que surgen de 1, 2, 3, 5 y un número infinito de orbitales

En las cuatro filas superiores de esta figura mostramos el caso con 1, 2, 3 y 5 bloques de construcción. A la izquierda de cada fila, mostramos el patrón de división de energía en el que evolucionan los orbitales de los bloques constructivos a medida que se superponen y forman orbitales moleculares deslocalizados. No es sorprendente, pues\(n = 2\), se encuentra una unión y una orbital antiadherentes. Porque\(n = 3\), uno tiene un orbital de unión, uno sin unión y uno antiadhesión. Por último, en la fila inferior, intentamos mostrar lo que sucede para una cadena infinitamente larga. El punto clave es que el número discreto de orbitales moleculares que aparecen en los casos orbitales 1-5 evoluciona hacia un continuo de orbitales llamado banda a medida que el número de bloques de construcción aumenta. Esta banda de energías orbitales va desde su parte inferior (cuyo orbital consiste en una combinación de unión completamente en fase de los orbitales del bloque de construcción) hasta su parte superior (cuyo orbital es una combinación antienlace completamente desfasada).

En la Figura 2.6 ilustramos estos orbitales de banda completamente ligados y completamente antiadhesión para dos casos: la parte inferior involucra orbitales de bloques de construcción tipo s y la parte superior con orbitales de\(p_\sigma\) tipo. Observe que cuando la brecha de energía entre el bloque de construcción\(s\) y\(p_\sigma\) los orbitales es mayor que la dispersión (dispersión) en la energía dentro de la banda\(s\) o banda de\(p_\sigma\) orbitales, se produce una brecha de banda entre el miembro más alto de la\(s\) banda y el miembro más bajo del \(p_\sigma\)banda. La división entre los\(p_\sigma\) orbitales\(s\) y es una propiedad de los átomos individuales que comprenden el sólido y varía entre los elementos de la tabla periódica. Por ejemplo, enseñamos a los estudiantes que la brecha\(2s\) -\(2p\) energía en C es menor que la\(3p\) brecha\(3s\) - en Si, que es menor que la\(4p\) brecha\(4s\) - en Ge. La dispersión en energías en la que se divide una banda dada de orbitales a medida que estos orbitales atómicos se combinan para formar una banda está determinada por la fuerza con la que se superponen los orbitales en los átomos vecinos. La superposición pequeña produce una dispersión pequeña y la superposición grande produce una banda ancha. Entonces, la estructura de bandas de cualquier sistema en particular puede variar desde una en la que bandas estrechas (superposición débil) no abarcan la brecha de energía entre las energías de sus orbitales atómicos constituyentes hasta bandas que se superponen fuertemente (gran superposición).

Figura 2.6. La unión a través de energías antiadherentes y orbitales de banda que surgen de\(s\) y de orbitales\(p_\sigma\) atómicos.

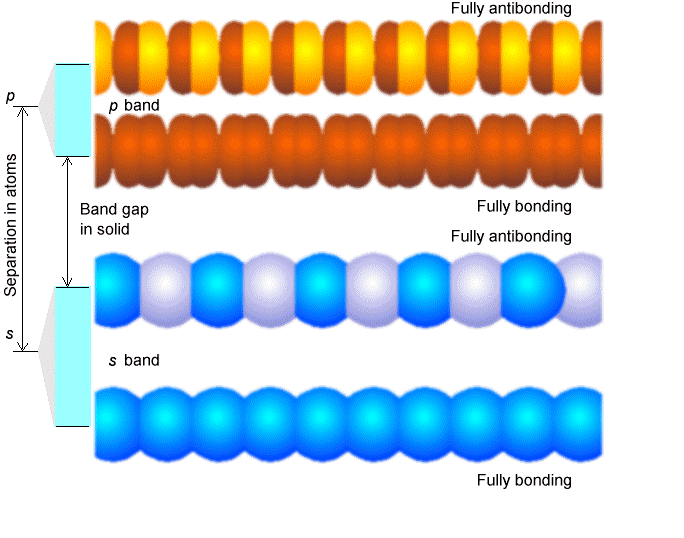
Dependiendo de cuántos electrones de valencia contribuya cada bloque de construcción, las diversas bandas formadas por la superposición de los orbitales de bloques de construcción de los átomos constituyentes se llenarán a varios niveles. Por ejemplo, si cada bloque de construcción orbital mostrado arriba tiene un solo electrón de valencia en un orbital s (por ejemplo, como en el caso de los metales alcalinos), la banda s se llenará a la mitad en el estado fundamental con electrones apareados a y b. Dichos sistemas producen muy buenos conductores porque sus\(s\) bandas parcialmente llenas permiten que los electrones se muevan con muy poca excitación (por ejemplo, solo térmica) entre otros orbitales en esta misma banda. Por otro lado, para los sistemas alcalinotérreos con dos\(s\) electrones por átomo, la banda s estará completamente llena. En tales casos, la conducción requiere excitación a los miembros más bajos de la banda orbital p cercana. Finalmente, si cada bloque de construcción fuera un átomo de Al (3s ² 3p ¹), la banda s estaría llena y la banda p estaría medio llena. En la Figura 2.6 a, se muestra una representación cualitativa de las bandas que surgen de los átomos de sodio\(1s\)\(2s\),\(2p\), y\(3s\) orbitales. Observe que la\(1s\) banda es muy estrecha porque hay poco acoplamiento entre\(1s\) orbitales vecinos, por lo que solo están ligeramente estabilizados o desestabilizados en relación con sus energías en los átomos de Na aislados. En contraste, las\(2p\) bandas\(2s\) y muestran una mayor dispersión (es decir, son más anchas), y la\(3s\) banda es aún más ancha. \(2p\)Las bandas\(1s\)\(2s\),, y están llenas, pero la\(3s\) banda está medio llena, como resultado de lo cual el Na sólido es un buen conductor eléctrico.

Figura 2.6 a. Ejemplo de átomos de sodio,\(1s\)\(2s\)\(2p\), y\(3s\) orbitales que se dividen en bandas llenas y parcialmente rellenas en metal de sodio.

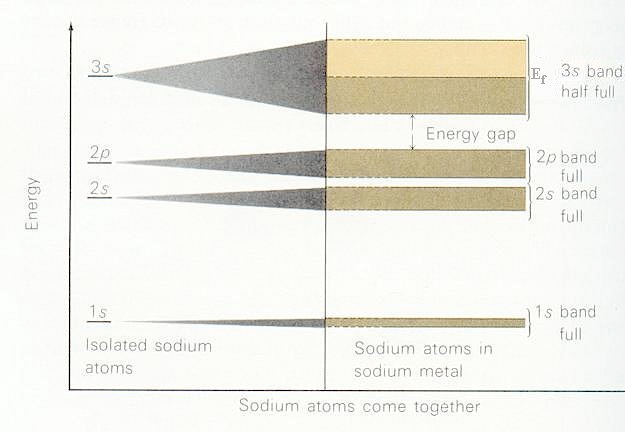
Al describir la banda de estados que surgen de un orbital atómico dado dentro de un sólido, es común mostrar la variación en las energías de estos estados como funciones del número de cambios de signo en los coeficientes que describen cada orbital como una combinación lineal de los orbitales atómicos constituyentes. Utilizando como ejemplo la matriz unidimensional de\(p_{\sigma}\) orbitales\(s\) y los orbitales mostrados en la Figura 2.6,

1. El miembro más bajo de la banda que deriva de los\(s\) orbitales\[ \phi_o = s(1) + s(2) +s(3) + s(4) ... + s(N) \tag{2.1}\] es una combinación de unión total de todos\(s\) los orbitales constituyentes en los\(N\) sitios de la red.
2. El orbital de mayor energía en esta banda\[\phi_N=s(1)- s(2) +s(3) - s(4) ... + s(N-1) + s(N) \tag{2.2}\] es una combinación totalmente antiunión de los\(s\) orbitales constituyentes.
3. Cada uno de los orbitales intermedios en esta banda tiene coeficientes de expansión que permiten que el orbital se escriba como\[\phi_n = \sum_{j=1}^N \cos \left( \dfrac{n(j-1)\pi}{N}\right)s(j)\tag{2.3}.\] Claramente, para valores pequeños de\(n\), la serie de coeficientes de expansión\(\cos \left( \dfrac{n(j-1)\pi}{N}\right) \tag{2.4}\) tiene pocos cambios de signo ya que el índice\(j\) recorre los sitios de la red unidimensional. Para mayor n, hay más cambios de signo. Así, pensando en el número cuántico\(n\) como etiquetar el número de cambios de signo y trazar las energías de los orbitales (en el eje vertical) versus\(n\) (en el eje horizontal), obtendríamos una gráfica que aumenta de\(n = 0\) a\(n =N\). De hecho, tales parcelas tienden a mostrar variación cuadrática de la energía con\(n\). Esta observación se puede entender dibujando una analogía entre el patrón de cambios de signo pertenecientes a un valor particular de\(n\) y el número de nodos en la función de onda unidimensional de partículas en una caja, que también se utiliza para modelar estados electrónicos deslocalizados a lo largo de una cadena lineal. Como vimos en el Capítulo 1, las energías para este sistema modelo variaron como\[ E= \dfrac{j^2\pi^2\hbar^2}{2mL^2} \tag{2.5}\]\(j\) siendo el número cuántico que iba desde\(1\) hasta\(\infty\). El estado de menor energía, con\(j = 1\), no tiene nodos; el estado con\(j = 2\) tiene un nodo, y el con\(j = n\) tiene\((n-1)\) nodos. Entonces, si reemplazamos\(j\) por\((n-1)\) y reemplazamos la longitud de la caja\(L\) por\((NR)\), donde\(R\) esta el espaciamiento entre atomos y\(N\) es el numero de atomos en la cadena, obtenemos\[ E= \dfrac{(n-1)^2\pi^2\hbar^2}{2mN^2R^2}\] de donde podemos ver por qué se puede esperar que la energía varíe como\((n/N)^2\).
4. En contraste para los\(p_{\sigma}\) orbitales, el orbital de menor energía se\[\phi_o=p_{\sigma}(1)- p_{\sigma}(2) +p_{\sigma}(3) - p_{\sigma}(4) ... - p_{\sigma}(N-1) + p_{\sigma}(N) \tag{2.6}\] debe a que esta alternancia en los signos permite que cada orbital en un sitio se superponga de manera ligante con los orbitales en sitios vecinos.
5. Por lo tanto, el orbital de mayor energía en la banda es\[\phi_o=p_{\sigma}(1) + p_{\sigma}(2) +p_{\sigma}(3) + p_{\sigma}(4) ... + p_{\sigma}(N-1) + p_{\sigma}(N) \tag{2.7}\] y es totalmente antiadherentes.
6. Los miembros intervinientes de esta banda tienen orbitales dados por\[\phi_{N-n} = \sum_{j=1}^N \cos \left( \dfrac{n(j-1)\pi}{N}\right)s(j) \tag{2.3}\] con bajos\(n\) correspondientes a orbitales de alta energía (con pocos cambios en el signo interatómico pero carácter antienlace) y orbitales de alta\(n\) a baja energía (teniendo muchos cambios en los signos interatómicos). Entonces, en contraste con el caso de los orbitales de banda s, trazando las energías de los orbitales (en el eje vertical) versus\(n\) (en el eje horizontal), obtendríamos una gráfica que disminuye de\(n = 0\) a\(n =N\).

Para las bandas compuestas por\(p_{\pi}\) orbitales, las energías varían con el número\(n\) cuántico de una manera análoga a cómo varía la\(s\) banda porque el orbital sin cambios de signo interatómico se une completamente. Para celosías bidimensionales y tridimensionales compuestas por orbitales s, p y d en los átomos constituyentes, el comportamiento de las bandas derivadas de estos orbitales sigue tendencias análogas. Es común describir las alternancias de signos que surgen de sitio a sitio en términos de un llamado\(\textbf{k}\) vector. En el caso unidimensional discutido anteriormente, este vector tiene solo un componente con elementos etiquetados por la relación (\(n/N\)) cuyo valor caracteriza el número de cambios en el signo interatómico. Para las celosías que contienen muchos átomos,\(N\) es muy grande, por lo que\(n\) va de cero a un número muy grande. Así, la relación (\(n/N\)) varía de cero a la unidad en pequeños pasos fraccionarios, por lo que es común pensar en estas proporciones como la descripción de un parámetro continuo que varía de cero a uno. Además, es convención permitir que el\(n\) índice oscile de\(–N\) a\(+N\), por lo que el argumento\(n \pi /N\) en la función coseno introducida anteriormente varía de\(-\pi\) a\(+\pi\).

En dos o tres dimensiones el\(\textbf{k}\) vector tiene dos o tres elementos y puede escribirse en términos de sus dos o tres relaciones de índice, respectivamente, como

\[\textbf{k}_2=\Big(\dfrac{n}{N},\dfrac{m}{M}\Big)\]

\[\textbf{k}_3=\Big(\dfrac{n}{N},\dfrac{m}{M},\dfrac{l}{L}\Big).\]

Aquí,,\(N\)\(M\), y\(L\) describiría el número de celdas unitarias a lo largo de los tres ejes principales del cristal tridimensional;\(N\) y\(M\) haría lo mismo en el caso de la celosía bidimensional.

En tales casos cristalinos bidimensionales y tridimensionales, las energías de los orbitales dentro de las bandas derivadas de los orbitales atómicos s, p, d, etc. muestran variaciones que también reflejan el número de cambios en los signos interatómicos. Sin embargo, ahora hay variaciones como funciones de los índices (\(n/N\)), (\(m/M\)) y (\(l/L\)), y estas variaciones pueden mostrar formas bastante complicadas dependiendo de la simetría de los átomos dentro de la red cristalina subyacente. Es decir, a medida que uno se mueve dentro del espacio tridimensional especificando valores de los índices (\(n/N\)), (\(m/M\)) y (\(l/L\)), uno puede moverse por toda la celosía en diferentes direcciones de simetría. Es convencional en la literatura de estado sólido trazar las energías de estas bandas, ya que estos tres índices varían de sitio a sitio a lo largo de varios elementos de simetría del cristal y asignar una letra para etiquetar este elemento de simetría. La banda que no tiene cambios en el signo interatómico se etiqueta como\(\Gamma\) (a veces G) en tales parcelas de estructuras de banda. En gran parte de nuestra discusión a continuación, analizaremos el comportamiento de varias bandas en la vecindad del\(\Gamma\) punto porque aquí es donde hay menos nodos interatómicos y así la función de onda es más fácil de visualizar.

Consideremos algunos ejemplos para ayudar a aclarar estos temas. En la Figura 2.6 b, donde vemos la estructura de bandas del grafeno, se pueden ver las variaciones cuadráticas de las energías con a\(\textbf{k}\) medida que uno se aleja del\(\textbf{k} = 0\) punto etiquetado\(\Gamma\), con algunas bandas aumentando con\(\textbf{k}\) y otras disminuyendo con\(\textbf{k}\).

Figura 2.6 b Gráfica de estructura de banda para grafeno.

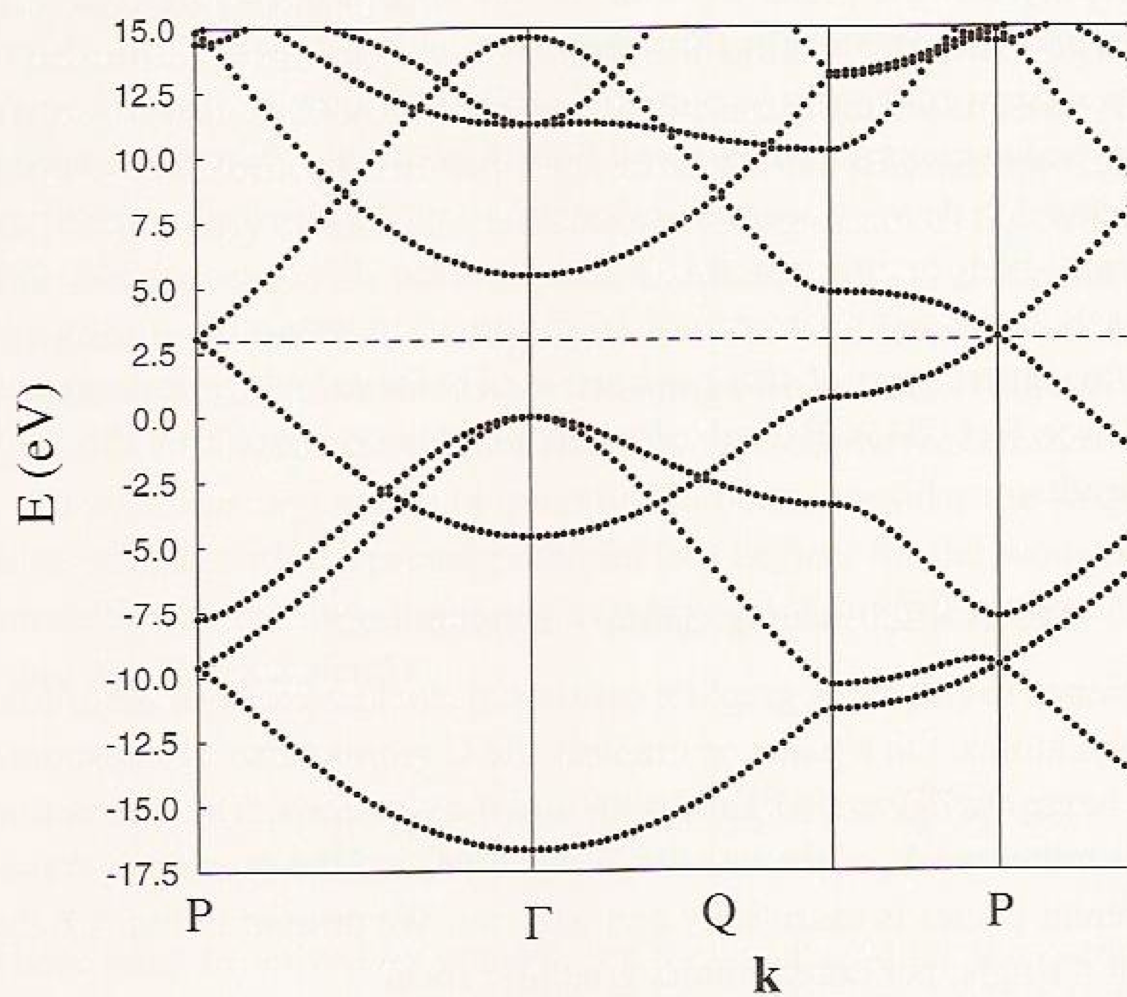
La banda que tiene una energía de ca. -17 eV en el\(\Gamma\) punto se origina a partir de interacciones de enlace que involucran\(2s\) orbitales en los átomos de carbono, mientras que las que tienen energías cercanas a 0 eV en el\(\Gamma\) punto derivan de interacciones de\(2p_\sigma\) enlace de carbono. El aumento parabólico con\(\textbf{k}\) para el\(2s\) basado y la disminución con\(\textbf{k}\) para los orbitales\(2p_\sigma\) basados es claro y se espera con base en nuestra discusión anterior de cómo\(\sigma\) y\(p_{\sigma}\) las bandas varían con\(\textbf{k}\). La banda que tiene energía cerca de -4 eV en el\(\Gamma\) punto involucra\(2p_\pi\) orbitales involucrados en interacciones de unión, y esta banda muestra un aumento parabólico con\(\textbf{k}\) lo esperado a medida que nos alejamos del\(\Gamma\) punto. Estos son los\(\pi\) orbitales deslocalizados de la lámina de grafeno. La\(2p_\pi\) banda antiunión disminuye cuadráticamente con\(\textbf{k}\) y tiene una energía de ca. 15 eV en el\(\Gamma\) punto. Debido a que en este caso hay dos átomos por celda unitaria, hay un total de ocho electrones de valencia (cuatro de cada átomo de carbono) para acomodarse en estas bandas. Los ocho electrones de valencia de carbono llenan la unión\(2s\) y dos\(2p_\sigma\) bandas completamente así como la\(2p_\pi\) banda de unión. Solo a lo largo de la dirección etiquetada P en la Figura 2.6b\(2p_\pi\) las bandas de unión y antiunión se degeneran (cerca de 2.5 eV); el enfoque de estas dos bandas es lo que permite que el grafeno sea semimetálico (es decir, conduzca a temperaturas modestas, lo suficientemente altas como para promover las excitaciones de la unión \(2p_\pi\)a la\(2p_\pi\) banda antiadherencia).

Es interesante contrastar la estructura de bandas del grafeno con la del diamante, que se muestra en la Figura 2. 6 c.

Figura 2.6 c Estructura de banda de carbono diamantado.

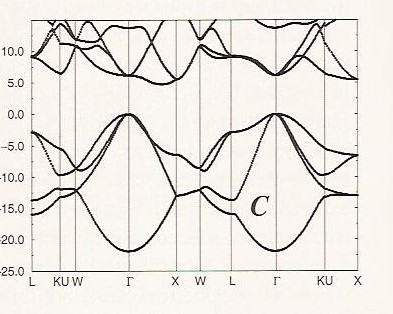
La banda que tiene una energía de ca. — 22 eV en el\(\Gamma\) punto deriva de interacciones de\(2s\) unión, y las tres bandas cercanas a 0 eV en el\(\Gamma\) punto provienen de interacciones de\(2p_\sigma\) unión. Nuevamente, cada una de estas bandas muestra el comportamiento parabólico esperado como funciones de\(\textbf{k}\). En la estructura cúbica interpenetrante centrada en la cara del diamante, hay dos átomos de carbono por celda unitaria, por lo que tenemos un total de ocho electrones de valencia para llenar las cuatro bandas de unión. Observe que a lo largo\(\textbf{k}\) de ninguna dirección en el espacio estas bandas de unión rellenas se degeneran con o son cruzadas por alguna de las otras bandas. Las otras bandas permanecen a mayor energía a lo largo de todas las\(\textbf{k}\) direcciones, y por lo tanto hay un espacio entre las bandas de unión y las otras es grande (ca. 5 eV o más a lo largo de cualquier dirección en\(\textbf{k}\) el espacio). Es por ello que el diamante es un aislante; la banda prohibida es muy grande.

Finalmente, comparemos los casos de grafeno y diamante con una caja metálica como la que se muestra en la Figura 2. 6 d para Al y para Ag.

Figura 2.6 d Estructuras de banda de Al y Ag.

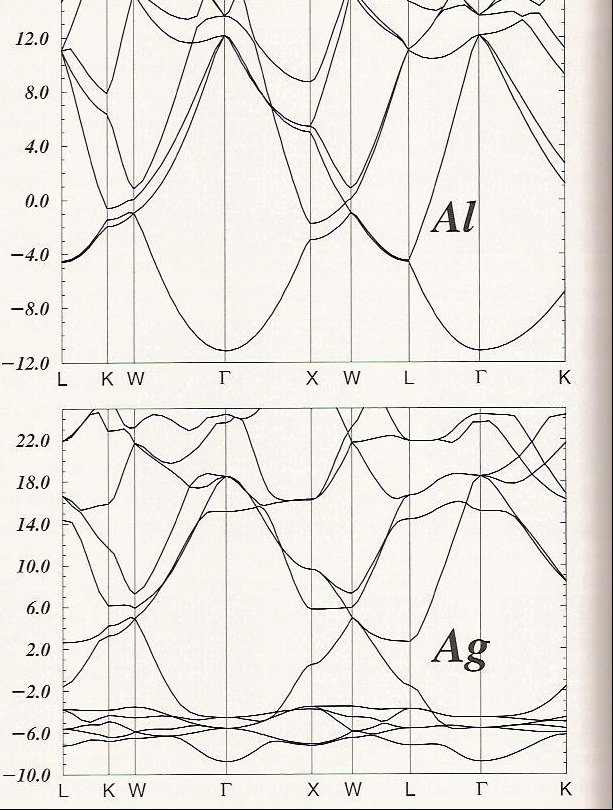
Para Al y Ag, hay un átomo por celda unitaria, por lo que tenemos tres electrones de valencia (3s ² 3p ¹) y once electrones de valencia (3d ¹⁰ 4s ¹), respectivamente, para llenar las bandas mostradas en la Figura 2.6d. Centrándonos en los\(\Gamma\) puntos en las tramas de estructura de bandas Al y Ag, podemos decir lo siguiente:

1. Para Al, la banda\(3s\) basada cerca de -11 eV se llena y las tres bandas\(3p\) basadas cerca de 11 eV tienen una ocupación de 1/6 (es decir, en promedio hay un electrón en una de estas tres bandas cada una de las cuales puede contener dos electrones).
2. \(3p\)Las bandas\(3s\) y son parabólicas con curvatura positiva y negativa, respectivamente.
3. A lo largo de varias direcciones (por ejemplo\(K\)\(W\)\(X\)\(W\),,,,\(L\)) hay cruces entre las bandas; estos cruces permiten que los electrones sean promovidos de bandas ocupadas a bandas previamente desocupadas. La ocupación parcial de las\(3p\) bandas y los múltiples cruces de bandas son lo que permite que Al muestre un comportamiento metálico.
4. Para Ag, hay seis bandas entre -4 eV y -8 eV. Cinco de estas bandas cambian poco con\(\textbf{k}\), y una muestra una dependencia algo parabólica de\(\textbf{k}\). Los cinco primeros derivan de orbitales\(4d\) atómicos que se contraen lo suficiente como para no permitir que se superpongan mucho, y el segundo se basa en la interacción orbital de\(5s\) unión.
5. Diez de los electrones de valencia llenan las cinco\(4d\) bandas, y el undécimo reside en la banda de unión basada en 5.
6. Si se ignoran las cinco bandas\(4d\) basadas, el resto de la estructura de la banda Ag se parece mucho a eso para Al. Existen numerosos cruces de bandas que incluyen, en particular, la\(5s\) banda medio llena. Estos cruces y la ocupación parcial de la\(5s\) banda hacen que el Ag tenga carácter metálico.

Una característica más de las estructuras de banda que a menudo se muestra se llama densidad de banda de estados. Un ejemplo de dicha gráfica se muestra en la Figura 2.6 e para el cristal de TiN.

Figura 2.6 e. Energías de bandas orbitales en TiN a lo largo\(\textbf{k}\) de diversas direcciones en el espacio (izquierda) y densidades de estados (derecha) como funciones de energía para este mismo cristal.

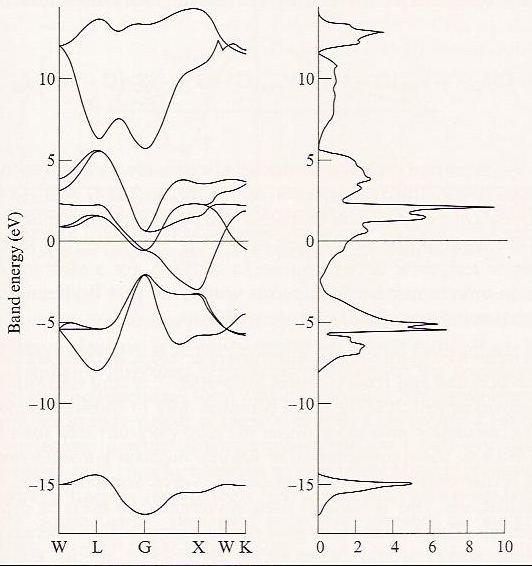
La densidad de estados a la energía\(E\) se calcula sumando todos aquellos orbitales que tienen una energía entre\(E\) y\(E + dE\). Claramente, como se ve en la Figura 2.6e, para bandas en las que las energías orbitales varían fuertemente con\(\textbf{k}\) (es decir, las llamadas bandas anchas), la densidad de estados es baja; en contraste, para bandas estrechas, la densidad de estados es alta. Las densidades de los estados son importantes porque sus energías y dispersiones de energía se relacionan con características espectrales electrónicas. Además, así como los huecos entre las bandas ocupadas más altas y las bandas desocupadas más bajas juegan un papel central en la determinación de si la muestra es un aislante, un conductor o un semiconductor, los huecos en la densidad de estados sugieren qué frecuencias de luz serán absorbidas o reflejadas a través de la electrónica inter-banda transiciones.

Las bandas de orbitales que surgen en cualquier red sólida proporcionan los orbitales que están disponibles para ser ocupados por el número de electrones en el cristal. Los sistemas cuya banda ocupada de energía más alta está completamente llena y para los cuales la brecha de energía a la banda más baja sin llenar es grande se denominan aislantes porque no tienen manera de promover fácilmente (es decir, con poco requerimiento de energía) algunos de sus electrones de mayor energía de orbital a orbital y así efectuar conducción. El caso del diamante discutido anteriormente es un ejemplo de un aislante. Si el espacio de banda entre una banda llena y una banda no llena es pequeño, puede ser posible que la excitación térmica (es decir, colisiones con átomos o moléculas vecinas) provoque la excitación de electrones desde el primero hasta el último induciendo un comportamiento conductor. Las estructuras de bandas de Al y Ag discutidas anteriormente ofrecen ejemplos de este caso. Una simple representación de cómo las excitaciones térmicas pueden inducir la conducción se ilustra en la Figura 2.7.

Figura 2.7. Las bandas de valencia y conducción y la banda gap con un espacio lo suficientemente pequeño como para permitir la excitación térmica para excitar electrones y crear agujeros en una banda previamente llena.

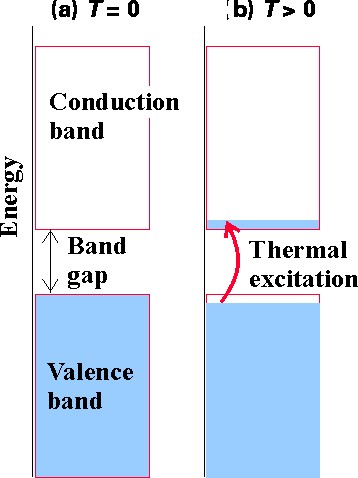
Los sistemas cuya banda ocupada de mayor energía está parcialmente llena también son conductores porque tienen poco espacio entre sus orbitales ocupados y desocupados para que los electrones puedan fluir fácilmente de uno a otro. Al y Ag son buenos ejemplos.

Para formar un semiconductor, se inicia con un aislante cuya banda inferior está llena y cuya banda superior está vacía como muestran las bandas anchas en la Fig. 2.8.

Figura 2.8. Las bandas llenas y vacías, el espacio de banda y las bandas aceptoras vacías o donantes rellenas.

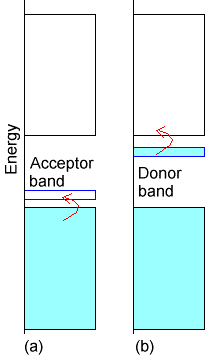
Si este material aislante se sintetiza con una pequeña cantidad de “dopante” cuyos orbitales de valencia tienen energías entre las bandas llenas y vacías del aislante, se puede generar un semiconductor. Si la especie dopante no tiene electrones de valencia (es decir, tiene un orbital de valencia vacía), da lugar a una banda vacía que se encuentra entre las bandas llenas y vacías del aislante como se muestra a continuación en el caso a de la Figura 2.8. En este caso, la banda dopante puede actuar como un aceptor de electrones para electrones excitados (ya sea térmicamente o por luz) desde la banda llena del aislante hacia la banda vacía del dopante. Una vez que los electrones entran en la banda dopante, la carga puede fluir (porque la banda inferior del aislador ya no está llena) y el sistema se convierte así en un conductor. Otro caso se ilustra en la parte b de la Figura 2.8. Aquí, el dopante tiene una banda llena que se encuentra cerca en energía de la banda vacía del aislante. La excitación de electrones de esta banda dopante a la banda vacía del aislador puede inducir el flujo de corriente (porque ahora la banda superior del aislador ya no está vacía).

Colaboradores y Atribuciones

Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

Integrated by Tomoyuki Hayashi (UC Davis)