2.8: Rotaciones de Moléculas

Movimiento de rotación para moléculas rígidas diatómicas y poliatómicas lineales

Esta ecuación de Schrödinger se relaciona con la rotación de moléculas poliatómicas diatómicas y lineales. También surge al tratar los movimientos angulares de electrones en cualquier potencial esféricamente simétrico.

Una molécula diatómica con longitud de enlace fija que\(R\) gira en ausencia de cualquier potencial externo se describe mediante la siguiente ecuación de Schrödinger:

\ [-\ frac {\ hbar^2} {2\ mu}\ izquierda [
\ frac {1} {R^2\ sin\ theta}\ frac {\ parcial} {\ parcial\ theta}\ izquierda (\ sin\ theta\ frac {\ parcial} {\ parcial\ theta}\ derecha)
+
\ frac {1} {R^2\ sin^2\ theta}\ frac {\ parcial^2} {\ parcial\ phi^2}
\ derecha]\ psi = E\ psi\]

o

\[\frac{\textbf{L}^2\psi}{2\mu R^2} = E \psi,\]

donde\(\textbf{L}^2\) es el cuadrado del operador de momento angular total\(\textbf{L}_x^2 + \textbf{L}_y^2 + \textbf{L}_z^2\) expresado en las coordenadas polares arriba. Los ángulos\(\theta\) y\(\phi\) describen la orientación del eje de la molécula diatómica en relación con un sistema de coordenadas fijado en laboratorio, y\(\mu\) es la masa reducida de la molécula diatómica\(\mu=\dfrac{m_1m_2}{m_1+m_2}\). Se puede ver que los operadores diferenciales son exactamente los mismos que los que surgieron en el caso del átomo similar al hidrógeno discutido anteriormente en este Capítulo. Por lo tanto, los mismos armónicos esféricos que sirvieron como las partes angulares de la función de onda en el caso del átomo de hidrógeno ahora sirven como la función de onda completa para el llamado rotor rígido:\(\psi = Y_{J,M}(\theta,\phi)\). Estas son exactamente las mismas funciones que trazamos antes cuando graficamos los\(s (L=0)\),\(p (L=1)\), y\(d (L=2)\) orbitales. Los valores propios de energía correspondientes a cada una de tales funciones propias se dan como:

\[E_J = \frac{\hbar^2 J(J+1)}{2\mu R^2} = B J(J+1)\]

y son independientes de\(M\). Así, cada nivel de energía está etiquetado por\(J\) y es\(2J+1\) -fold degenerado (porque\(M\) va desde\(-J\) hasta\(J\)). Nuevamente, esto es como vimos cuando miramos los orbitales de hidrógeno; los orbitales p son 3 veces degenerados y los orbitales d son 5 veces degenerados. La llamada constante rotacional\(B\) (definida como\(\dfrac{\hbar^2}{2\mu R^2}\)) depende de la longitud del enlace de la molécula y de la masa reducida. Los espaciamientos entre niveles rotacionales sucesivos (que son de relevancia espectroscópica porque, como se muestra en el Capítulo 6, las reglas de selección de momento angular a menudo restringen los cambios\(\Delta J\) en\(J\) que pueden ocurrir tras la absorción de fotones a 1,0, y -1) están dadas por

\[\Delta E = B (J+1)(J+2) - B J(J+1) = 2B(J+1).\]

Estos espaciamientos de energía son relevantes para la espectroscopia de microondas que sondea los niveles de energía rotacional de las moléculas. De hecho, la espectroscopia de microondas ofrece la forma más directa de determinar las constantes rotacionales moleculares y, por lo tanto, las longitudes de enlace molecular.

El rotor rígido proporciona la aproximación más comúnmente empleada a las energías rotacionales y las funciones de onda de las moléculas lineales. Como se presentó anteriormente, el modelo restringe la longitud de unión para ser fija. El movimiento vibracional de la molécula da lugar a cambios en\(R\), que luego se reflejan en cambios en los niveles de energía rotacional (es decir, existen diferentes\(B\) valores para diferentes niveles vibracionales). El acoplamiento entre movimiento rotacional y vibracional da lugar a\(B\) constantes rotacionales que dependen del estado vibracional así como acoplamientos dinámicos, llamados distorsiones centrífugas, que hacen que la energía rovibracional total de la molécula dependa de los números cuánticos rotacionales y vibracionales de manera no separable.

Dentro de este modelo de rotor rígido, el espectro de absorción de una molécula diatómica rígida debe mostrar una serie de picos, cada uno de los cuales corresponde a una\(J \rightarrow J+1\) transición específica. Las energías a las que ocurren estos picos deben crecer linealmente con\(J\) como se muestra arriba. Un ejemplo de tal progresión de líneas rotacionales se muestra en la Figura 2.23.

Figura 2.23. Perfil típico de absorción rotacional que muestra intensidad vs.\(J\) valor del nivel de absorción

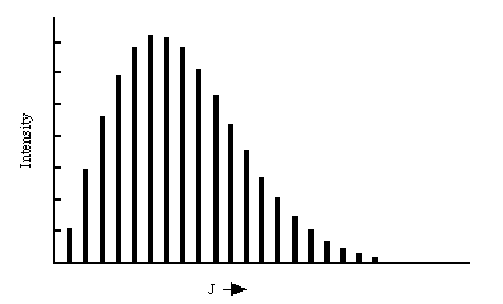
Las energías a las que ocurren las transiciones rotacionales parecen ajustarse bastante bien a la\(\Delta E = 2B (J+1)\) fórmula. Las intensidades de las transiciones de nivel\(J\) a nivel\(J+1\) varían fuertemente con\(J\) principalmente porque la población de moléculas en el nivel absorbente varía con\(J\). Estas poblaciones\(P_J\) se dan, cuando el sistema está en equilibrio a temperatura\(T\), en términos de la degeneración (\(2J+1\)) del nivel Jth y la energía de este nivel\(B J(J+1)\) por la fórmula de Boltzmann:

\[P_J = \frac{1}{Q} (2J+1) \exp\bigg(-\dfrac{BJ(J+1)}{kT}\bigg),\]

donde\(Q\) está la función de partición rotacional:

\[Q = \sum_J (2J+1) \exp\bigg(-\dfrac{BJ(J+1)}{kT}\bigg).\]

Para valores bajos de\(J\), la degeneración es baja y el\(\exp(-BJ(J+1)/kT)\) factor está cerca de la unidad. A medida que\(J\) aumenta, la degeneración crece linealmente pero el\(\exp(-BJ(J+1)/kT)\) factor disminuye más rápidamente. En consecuencia, existe un valor de\(J\), dado tomando la derivada de\((2J+1) \exp(-BJ(J+1)/kT)\) con respecto a\(J\) y poniéndola igual a cero,

\[2J_{\rm max}+ 1 =\sqrt{\frac{2kT}{B}}\]

en el que se espera que la intensidad de la transición rotacional alcance su máximo. Este comportamiento se muestra claramente en la figura anterior.

Las funciones propias que pertenecen a estos niveles de energía son los armónicos esféricos\(Y_{L,M}(\theta,\phi)\) que se normalizan de acuerdo con

\[\int_0^\pi\int_0^{2\pi}Y_{L,M}^*(\theta,\phi)Y_{L',M'}(\theta,\phi)\sin\theta d\theta d\phi= \delta_{L,L'} \delta_{m,m^\prime} .\]

Como se señaló anteriormente, estas funciones son idénticas a las que aparecen en la solución de la parte angular de los átomos hidrogénicos. Los niveles de energía y funciones propias anteriores también se aplican a la rotación de moléculas poliatómicas lineales rígidas; la única diferencia es que el momento de inercia I entrando en la expresión de energía rotacional, que es\(\mu R^2\) para un diatómico, viene dado por

\[I = \sum_a m_a R_a^2\]

donde ma es la masa del\(a^{\rm th}\) átomo y\(R_a\) es su distancia desde el centro de masa de la molécula a este átomo.

Movimientos rotacionales de moléculas rígidas no lineales

La energía cinética rotacional

La energía cinética rotacional clásica para una molécula poliatómica rígida es

\[H_{\rm rot} = \frac{J_a^2}{2I_a} + \frac{J_b^2}{2I_b}​ + \frac{J_c^2}{2I_c}​\]

donde\(I_k (k = a, b, c)\) están los tres momentos principales de inercia de la molécula (los valores propios del momento de inercia tensor). Este tensor tiene elementos en un sistema de coordenadas cartesianas (\(K, K' = X, Y, Z\)), cuyo origen se localiza en el centro de masa de la molécula, que pueden computarse como:

\[I_{K,K} = \sum_j m_j (R_j^2 - R_{K,j}^2) \hspace{1cm} (\text{for }K = K')\]

\[I_{K,K'} = - \sum_j m_j R_{K,j} R_{K',j} \hspace{1cm} (\text{for } K \ne K').\]

Como se discutió con más detalle en R. N. Zare, Angular Momentum, John Wiley, Nueva York (1988), los componentes de los correspondientes operadores de momento angular mecánico cuántico a lo largo de los tres ejes principales son:

\[\textbf{J}_a = -i\hbar \cos\chi \left[\cot\theta \frac{\partial}{\partial \chi} - \frac{1}{\sin\theta}\frac{\partial}{\partial \phi} \right] -i\hbar \sin\chi \frac{\partial}{\partial \theta}\]

\[\textbf{J}_b = i\hbar​ \sin\chi \left[\cot\theta \frac{\partial}{\partial \chi} - \frac{1}{\sin\theta}\frac{\partial}{\partial \phi}\right] -i\hbar \cos\chi \frac{\partial}{\partial \theta}\]

\[\textbf{J}_c = - i\hbar \frac{\partial}{\partial \chi} .\]

Los ángulos\(\theta\)\(\phi\), y\(\chi\) son los ángulos de Euler necesarios para especificar la orientación de la molécula rígida en relación con un sistema de coordenadas fijado en laboratorio. El cuadrado correspondiente del operador de momento angular total se\(\textbf{J}^2\) puede obtener como

\[\textbf{J}^2 = \textbf{J}_a^2 + \textbf{J}_b^2 + \textbf{J}_c^2\]

\[= - \hbar^2 \frac{\partial^2}{\partial \theta^2} - \hbar^2\cot\theta \frac{\partial}{\partial \theta} + \hbar^2 \frac{1}{\sin^2\theta} \left[\frac{\partial^2}{\partial \phi^2} + \frac{\partial^2}{\partial \chi^2} - 2 \cos\theta\frac{\partial^2}{\partial \phi\partial \chi} \right],\]

y el componente a lo largo del laboratorio -\(Z\) eje fijo\(J_Z\) es\(- i\hbar \partial /\partial \phi\) como vimos mucho antes en este texto.

Las funciones propias y los valores propios para casos especiales

Tops esféricos

Cuando los tres valores principales del momento de inercia son idénticos, la molécula se denomina una parte superior esférica. En este caso, la energía rotacional total se puede expresar en términos del operador de momento angular total\(\textbf{J}^2 \)

\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I}.\]

Como resultado, las funciones propias de\(\textbf{H}_{\rm rot}\) son las de\(\textbf{J}^2\) y así\(J_a\) como\(J_Z\) ambas de las cuales viajan con\(\textbf{J}^2\) y entre sí. \(J_Z\)es el componente de\(J\) a lo largo del\(Z\) eje fijo de laboratorio y viaja con\(J_a\) porque\(J_Z = - i\hbar \partial /\partial \phi\) y\(J_a = - i\hbar \partial /\partial \chi\) actúa en diferentes ángulos. Las energías asociadas con tales funciones propias son

\[E(J,K,M) = \frac{\hbar^2​ J(J+1)}{2I^2},\]

para todos\(K\) (es decir, números\(J_a\) cuánticos) que van desde\(-J\) hasta\(J\) en pasos unitarios y para todos\(M\) (es decir, números\(J_Z\) cuánticos) que van desde\(-J\) hasta\(J\). Por lo tanto, cada nivel de energía es\((2J + 1)^2\) degenerado porque hay\(K\) valores\(2J + 1\) posibles y\(2J + 1\) posibles\(M\) valores para cada uno\(J\).

Las funciones propias\(|J,M,K\rangle \) de\(\textbf{J}^2\),\(J_Z\) y\(J_a\), se dan en términos del conjunto de las llamadas matrices de rotación\(D_{J,M,K}\):

\[|J,M,K\rangle = \sqrt{\frac{2J+1}{8\pi^2}}D^*_{J,M,K}(\theta,\phi,\chi)\]

que obedecen

\[\textbf{J}^2|J,M,K\rangle = \hbar^2 J(J+1) |J,M,K\rangle ,\]

\[\textbf{J}_a |J,M,K\rangle = \hbar K |J,M,K\rangle ,\]

\[\textbf{J}_Z |J,M,K\rangle = \hbar M |J,M,K\rangle .\]

Estas\(D_{J,M,K}\) funciones son proporcionales a los armónicos esféricos\(Y_{J,M}(\theta,\phi)\) multiplicados por\(\exp(iK\chi)\), lo que refleja su c-dependencia.

Tops simétricos

Las moléculas para las que dos de los tres momentos principales de inercia son iguales se denominan cimas simétricas. Aquellos para los que el momento único de inercia es menor que los otros dos se denominan cimas simétricas prolongadas; si el momento único de inercia es mayor que los otros, la molécula es una parte superior simétrica oblata. Un fútbol americano es prolado, y un Frisbee es oblato.

Nuevamente, la energía cinética rotacional, que es la hamiltoniana rotacional completa, se puede escribir en términos del operador de momento angular rotacional total\(\textbf{J}^2\) y la componente del momento angular a lo largo del eje con el único momento principal de inercia:

\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I} + \textbf{J}_a^2\left[\frac{1}{2I_a} - \frac{1}{2I}​\right]\text{, for prolate tops}\]

\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I} + \textbf{J}_c^2\left[\frac{1}{2I_c} - \frac{1}{2I}​\right]\text{, for oblate tops}\]

Aquí, el momento de inercia I denota ese momento que es común a dos direcciones; es decir, yo es el momento no único de inercia. Como resultado, las funciones propias de\(H_{\rm rot}\) son las de\(\textbf{J}^2\) y\(J_a\) o\(J_c\) (y de\(J_Z\)), y los niveles de energía correspondientes son:

\[E(J,K,M) = \frac{\hbar^2​ J(J+1)}{2I^2} + \hbar^2 K^2 \left[\frac{1}{2I_a} - \frac{1}{2I}​\right],\]

para tapas proladas

\[E(J,K,M) = \frac{\hbar^2​ J(J+1)}{2I^2} + \hbar^2 K^2 \left[\frac{1}{2I_c} - \frac{1}{2I}​\right],\]

para tops oblatos, nuevamente para\(K\) y\(M\) (es decir,\(J_a\) o\(J_c\) y números\(J_Z\) cuánticos, respectivamente) que van desde\(-J\) hasta\(J\) in unit steps. Since the energy now depends on \(K\), estos niveles solo son\(2J + 1\) degenerados debido a la\(2J + 1\) diferentes puntas\(M\) values that arise for each \(J\) value. Notice that for prolongadas, porque\(I_a\) is smaller than \(I\), las energías aumentan con el aumento de\(K\) for given \(J\). In contrast, for oblate tops, since \(I_c\) is larger than \(I\), the energies decrease with \(K\) for given \(J\). The las funciones propias\(|J, M,K\rangle \) are the same rotation matrix functions as arise for the spherical-top case, so they do not require any further discussion at this time.

iii. Tops Asimétricos

Las funciones propias rotacionales y los niveles de energía de una molécula para la que los tres momentos principales de inercia son distintos (una llamada parte superior asimétrica) no pueden expresarse analíticamente en términos de los estados propios de momento angular\(J, M,\) y los números\(K\) cuánticos. De hecho, nadie ha resuelto nunca la ecuación de Schrödinger correspondiente para este caso. Sin embargo, dados los tres momentos principales de inercia\(I_a\)\(I_b\), y\(I_c\), una representación matricial de cada una de las tres contribuciones a la rotación hamiltoniana

\[\textbf{H}_{\rm rot} = \frac{\textbf{J}_a^2}{2I_a} + \frac{\textbf{J}_b^2}{2I_b}​ + \frac{\textbf{J}_c^2}{2I_c}​\]

se puede formar dentro de un conjunto de bases de las {\(|J, M, K\rangle \)} funciones de matriz de rotación discutidas anteriormente. Esta matriz no será diagonal porque las\(|J, M, K\rangle \) funciones no son funciones propias de la parte superior asimétrica\(\textbf{H}_{\rm rot}\). Sin embargo, la matriz se puede formar en esta base y posteriormente llevarla a forma diagonal al encontrar sus vectores propios {\(C_{n, J,M,K}\)} y sus valores propios {\(E_n\)}. Los coeficientes vectoriales expresan los estados propios asimétricos superiores como

\[\psi_n (\theta,\phi,\chi) = \sum_{J, M, K} C_{n, J,M,K} |J, M, K\rangle .\]

Debido a que el momento angular total\(\textbf{J}^2\) aún viaja con\(H_{\rm rot}\), cada uno de esos autoestados contendrá solo un\(\textbf{J}_{-}\) valor y, por lo tanto, también\(\psi_n\) puede etiquetarse con un número\(J\) cuántico:

\[\psi_{n​,J} (\theta,\phi,\chi) = \sum_{M, K} C_{n, J,M,K} |J, M, K\rangle .\]

Para formar los únicos elementos de matriz distintos de cero\(H_{\rm rot}\) dentro de la\(|J, M, K\rangle \) base, se pueden usar las siguientes propiedades de las funciones rotación-matriz (ver, por ejemplo, R. N. Zare, Angular Momentum, John Wiley, New York (1988)):

\[\langle J, M, K| \textbf{J}_a^2| J, M, K\rangle = \langle J, M, K| \textbf{J}_b^2| J, M, K\rangle \]

\[= \frac{1}{2} \langle J, M, K| \textbf{J}^2 - \textbf{J}​_c^2 | J, M, K\rangle = \hbar^2 [ J(J+1) - K^2 ],\]

\[\langle J, M, K| \textbf{J}​_c^2| J, M, K\rangle = \hbar^2 K^2,\]

\[\langle J, M, K| \textbf{J}_a^2| J, M, K ± 2\rangle = - \langle J, M, K| \textbf{J}_b^2| J, M, K ± 2\rangle \]

\[= \hbar^2 \sqrt{J(J+1) - K(K± 1)} \sqrt{J(J+1) -(K± 1)(K± 2)}\]

\[\langle J, M, K| \textbf{J}​_c^2| J, M, K ± 2\rangle = 0.\]

Cada uno de los elementos de\(\textbf{J}_c^2\)\(\textbf{J}_a^2\),, y\(\textbf{J}_b^2\) debe, por supuesto, ser multiplicado, respectivamente\(\dfrac{1}{2I_c}\), por\(\dfrac{1}{2I_a}\),\(\dfrac{1}{2I_b}\) y sumado juntos para formar la representación matricial de\(H_{\rm rot}\). La diagonalización de esta matriz proporciona entonces las energías superiores asimétricas y las funciones de onda.

Colaboradores y Atribuciones

Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

Integrated by Tomoyuki Hayashi (UC Davis)