5.2: Estructura molecular- Teoría y Experimento
- Page ID
- 70815
Sondas Experimentales de Formas Moleculares
Espero que se pregunten por qué quiero discutir cómo los experimentos miden formas moleculares en este texto cuyo objetivo es introducirte en el campo de la química teórica. De hecho, la teoría y la medición experimental están muy conectadas, y son estas conexiones las que deseo enfatizar en la siguiente discusión. En particular, quiero dejar claro que los datos experimentales sólo pueden ser interpretados, y así utilizados para extraer propiedades moleculares, a través de la aplicación de la teoría. Entonces, la teoría no sustituye al experimento, sino que sirve tanto como componente complementario de la investigación química (via. simulación de propiedades moleculares) como como el medio por el cual conectamos los datos de laboratorio con las propiedades moleculares.
Espectroscopía Rotacional
La mayoría de nosotros usamos la excitación rotacional de moléculas en nuestra vida cotidiana. En particular, cuando cocinamos en un horno microondas, la radiación de microondas, que tiene una frecuencia en el\(10^9- 10^{11} s^{-1}\) rango, introduce energía en los movimientos rotacionales de las moléculas de agua (principalmente) contenidas en los alimentos. Estas moléculas de agua rotacionalmente calientes chocan con moléculas vecinas (es decir, otras aguas, así como proteínas y otras moléculas en los alimentos y en el recipiente de cocción) para transferirles parte de su energía de movimiento. A través de este medio, la energía cinética traslacional de todas las moléculas dentro de la olla gana energía. Este proceso de transferencia de energía de rotación a traslación es como la radiación de microondas finalmente calienta los alimentos, que los cocinan. ¿Qué sucede cuando pones la comida en el horno microondas en un recipiente metálico o con algún otro material metálico? Como se muestra en el Capítulo 2, los electrones en los metales existen en orbitales muy deslocalizados parcialmente llenos llamados bandas. Estos orbitales de banda se extienden por toda la pieza de metal. La aplicación de cualquier campo eléctrico externo (por ejemplo, el que pertenece a la radiación de microondas) hace que estos electrones metálicos se muevan por todo el metal. A medida que estos electrones acumulan cada vez más energía de la radiación de microondas, eventualmente tienen suficiente energía cinética para ser expulsados al aire circundante formando una descarga. Esto provoca las chispas que vemos cuando cometemos el error de poner cualquier cosa metálica en nuestro horno microondas. Ahora aprendamos más sobre cómo los fotones de microondas hacen que las moléculas se exciten rotacionalmente.
Usando radiación de microondas, las moléculas que tienen vectores de momento dipolo (\(\boldsymbol{\mu}\)) pueden ser hechas para someterse a excitación rotacional. En tales procesos, el campo eléctrico variable en el tiempo\(\textbf{E} \cos(\omega t)\) de la radiación electromagnética de microondas interactúa con las moléculas a través de una energía potencial de la forma\(V = \textbf{E} \cdot \boldsymbol{\mu} \cos(\omega t)\). Este potencial puede hacer que la energía fluya desde la fuente de energía de microondas hacia los movimientos rotacionales de la molécula cuando la energía de la primera\(\hbar\omega/2\pi\) coincide con la separación de energía entre dos niveles de energía rotacional.
Esta idea de hacer coincidir la energía de los fotones con los espaciamientos energéticos de la molécula ilustra el concepto de resonancia y es algo que es omnipresente en la espectroscopia como aprendimos en detalle matemático en el Capítulo 4. Al escuchar por primera vez que la energía del fotón debe coincidir con un espaciado de nivel de energía en la molécula para que ocurra la absorción de fotones, parece obvio e incluso trivial. Sin embargo, tras una reflexión adicional, hay más en tales requisitos de resonancia de lo que uno podría pensar. Permítame ilustrar usando este ejemplo de excitación rotacional inducida por microondas pidiéndole que considere por qué los fotones cuyas energías exceden\(\hbar\omega/2\pi\) considerablemente el espaciamiento energético no\(\Delta{E}\) serán absorbidos en esta transición. Es decir, ¿por qué la energía más que suficiente no es lo suficientemente buena? La razón es que para que dos sistemas (en este caso el campo eléctrico del fotón y la rotación de la molécula que hace que su momento dipolar también rote) interactúen y así intercambien energía (esto es lo que es la absorción de fotones), deben tener casi las mismas frecuencias. Si la frecuencia del fotón (\(\omega\)) excede la frecuencia de rotación de la molécula en una cantidad significativa, la molécula experimentará un campo eléctrico que oscila demasiado rápido para inducir un par en el dipolo de la molécula que siempre está en la misma dirección y que dura sobre una longitud significativa de tiempo. Como resultado, el campo eléctrico que oscila rápidamente no proporcionará una torsión coherente del dipolo y por lo tanto no inducirá excitación rotacional.
Un ejemplo sencillo de la vida cotidiana puede ilustrar aún más este tema. Cuando intentas empujar a tu amigo, cónyuge o hijo en un columpio, mueves tus brazos en resonancia con la frecuencia de movimiento de la persona oscilante. Cada vez que la persona regresa a ti, tus brazos te esperan para dar un empujón en la dirección que le dé energía al individuo oscilante. Esto sucede una y otra vez; cada vez que regresan, tus brazos han vuelto para estar listos para dar otro empujón en la misma dirección. En este caso, decimos que tus brazos se mueven en resonancia con el movimiento del swing y ofrecen una excitación coherente del swinger. Si aumentaras mucho la velocidad a la que tus brazos se mueven en su patrón hacia arriba y hacia abajo, la persona que se balancea no siempre experimentaría un empuje en la dirección correcta cuando regresen a encontrarse con tus brazos. A veces sentirían un fuerte empuje en fase, pero otras veces sentirían un empuje fuera de fase en la dirección opuesta. El resultado neto es que, a lo largo de un largo periodo de tiempo, sentirían tirones aleatorios desde tus brazos, y así no sufrirían una suave transferencia de energía de tu parte. Es por ello que una frecuencia demasiado alta (y por lo tanto una energía demasiado alta) no induce excitación. Volvamos ahora al caso de la excitación rotacional por fotones de microondas.
Como vimos en el Capítulo 2, para una molécula diatómica rígida, los espaciamientos de energía rotacional vienen dados por
\[E_{J+1} – E_J = 2 (J+1) \bigg(\dfrac{\hbar^2}{2I} \bigg) = 2\hbar c B (J+1) \tag{5.2.1}\]
donde
\(I\)es el momento de inercia de la molécula dado en términos de su longitud de enlace de equilibrio\(r_e\) y su masa reducida\(\mu=\dfrac{m_am_b}{m_a+m_b}\) como\(I = Mr_e^2\). Así, en principio, medir los espaciamientos del nivel de energía rotacional mediante espectroscopia de microondas permite determinar\(r_e\). La segunda identidad anterior simplemente define lo que se llama la constante rotacional\(B\) en términos del momento de inercia. Los niveles de energía rotacional descritos anteriormente dan lugar a un colector de niveles de espaciamiento no uniforme como se muestra en la Figura 5.13.
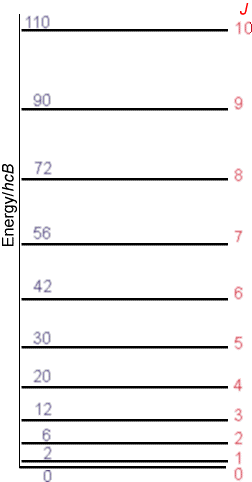
La falta de uniformidad en los espaciamientos es el resultado de la dependencia cuadrática de los niveles de energía rotacional\(E_J\) en el número cuántico rotacional\(J\):
\[ E_J = J(J+1) \bigg(\dfrac{\hbar^2}{2I}\bigg).\tag{5.2.2}\]
Además, el nivel con número cuántico\(J\) es\((2J+1)\) -fold degenerado; es decir, hay\(2J+1\) distintos estados de energía y funciones de onda que tienen energía\(E_J\) y que se distinguen por un número cuántico\(M\). Estos\(2J+1\) estados tienen energía idéntica pero difieren entre sí por la orientación de su momento angular en el espacio (es decir, la orientación de cómo están girando).
Para las moléculas poliatómicas, sabemos por el Capítulo 2 que las cosas son más complicadas porque los niveles de energía rotacional dependen de tres llamados momentos principales de inercia (\(I_a\),\(I_b\),\(I_c\)) que, a su vez, contienen información sobre la geometría de la molécula. Estos tres momentos principales se encuentran formando una matriz de momentos de inercia 3x3 que tiene elementos
\[I_{x,x} = \sum_a m_a [ (R_a-R_{\rm CofM})^2 -(x_a - x_{\rm CofM} )^2\tag{5.2.3a}\]
y
\[I_{x,y} = \sum_a ma [ (x_a - x_{\rm CofM}) ( y_a -y_{\rm CofM}) ]\tag{5.2.3b}\]
expresado en términos de las coordenadas cartesianas de los núcleos (a) y del centro de masa en un sistema de coordenadas arbitrarias de moléculas fijas (definiciones análogas se mantienen para\(I_{z,z}\)\(I_{y,y}\),\(I_{x,z}\) y\(I_{y,z}\)). Los momentos principales se obtienen entonces como los valores propios de esta matriz 3x3.
Para las moléculas con los tres momentos principales iguales, los niveles de energía rotacional están dados por\(E_{J,K} = \dfrac{\hbar^2J(J+1)}{2I}\), y son independientes del número\(K\) cuántico y del número\(M\) cuántico que describe de nuevo la orientación de cómo la molécula está girando en el espacio. Tales moléculas se llaman cimas esféricas. Para las moléculas (llamadas cimas simétricas) con dos momentos principales iguales (\(I_a\))) y un momento único\(I_c\), las energías dependen de dos números cuánticos\(J\) y\(K\) y están dadas por
\[E_{J,K} = \dfrac{\hbar^2J(J+1)}{2I_a} + \hbar^2K^2 \bigg(\dfrac{1}{2I_c} - \dfrac{1}{2I_a}\bigg). \tag{5.2.4}\]
Las especies que tienen los tres momentos principales de inercia únicos, denominados picos asimétricos, tienen niveles de energía rotacional para los cuales aún no se conoce una fórmula analítica. La molécula de H2O, mostrada en la Figura 5.14, es una molécula superior asimétrica de este tipo. Se dieron más detalles sobre las energías rotacionales y las funciones de onda en el Capítulo 2.
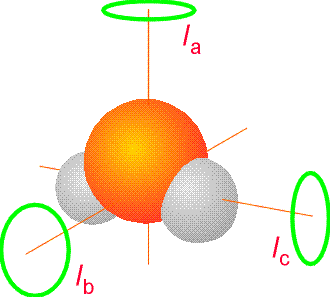
Los momentos de inercia que ocurren en las expresiones para los niveles de energía rotacional involucran posiciones de núcleos atómicos en relación con el centro de masa de la molécula. Entonces, un espectro de microondas puede, en principio, determinar los momentos de inercia y de ahí la geometría de una molécula. En la discusión dada anteriormente, tratamos estas posiciones, y así los momentos de inercia como fijos (es decir, no variando con el tiempo). Por supuesto, estas distancias no son inmutables con el tiempo en una molécula real porque los núcleos atómicos de la molécula experimentan movimientos vibracionales. Debido a esto, son los momentos de inercia promediados vibracionalmente los que deben incorporarse a las fórmulas de nivel de energía rotacional. Específicamente, debido a que las energías rotacionalmente dependen de las inversas de los momentos de inercia, se debe promediar vibracionalmente\((R_a–R_{\rm CofM})^{-2}\) sobre el movimiento vibratorio que caracteriza el movimiento de la molécula. Para especies que contienen enlaces rígidos, el promedio vibracional\(\langle \psi|(R_a –R_{\rm CofM})^{-2}|\psi\rangle \) de los cuadrados inversos de distancias atómicas en relación con el centro de masa no difiere significativamente de los valores de equilibrio
\((R_{a,eq} –R_{\rm CofM})^{-2}\)de las mismas distancias. Sin embargo, para moléculas como complejos débiles de van der Waals (por ejemplo, (H2O) 2 o Ar.. HCl) que experimentan movimientos vibracionales de gran amplitud flojos, puede haber grandes diferencias entre el equilibrio\((R_{a,eq} –R_{\rm CofM})^{-2}\) y los valores promediados por vibración\(\langle \psi|(R_a –R_{\rm CofM})^{-2}|\psi\rangle \). El tratamiento adecuado de los patrones de nivel de energía rotacional en tales moléculas flojas todavía está muy bajo estudio activo por químicos teóricos y experimentales. Por esta razón, es una tarea muy desafiante usar datos de microondas sobre energías rotacionales para determinar geometrías (equilibrio o promediado vibracionalmente) para este tipo de moléculas.
Entonces, en el área de la espectroscopia rotacional la teoría juega varios papeles importantes:
- Proporciona las ecuaciones básicas en términos de las cuales las separaciones de líneas rotacionales se relacionan con momentos de inercia.
- Permite, dada la distribución de longitudes de enlace geométricas y ángulos característicos del estado vibratorio en el que existe la molécula, calcular el momento de inercia promedio vibracional adecuado.
- Se puede utilizar para tratar movimientos disquetes de gran amplitud (por ejemplo, simulando los movimientos nucleares en una superficie de energía de Born-Oppenheimer), permitiendo así que los espectros resueltos rotacionalmente de tales especies proporcionen información adecuada sobre el momento de inercia (y por lo tanto la geometría).
Espectroscopía Vibracional
La capacidad de las moléculas para absorber y emitir radiación infrarroja a medida que experimentan transiciones entre sus niveles de energía vibratoria es fundamental para la salud de nuestro planeta. Resulta que el agua y\(CO_2\) las moléculas tienen enlaces que vibran en el rango de\(10^{13}-10^{14} s^{-1}\) frecuencia que se encuentra dentro del espectro infrarrojo (\(10^{11} –10^{14} s^{-1}\)). Como la radiación solar (principalmente visible y ultravioleta) impacta la superficie terrestre, es absorbida por moléculas con transiciones electrónicas en este rango de energía (por ejemplo, moléculas coloreadas como las contenidas en las hojas de las plantas y otro material oscuro). Estas moléculas son promovidas con ello a estados electrónicos excitados. Algunas de esas moléculas reemiten los fotones que las excitaron pero la mayoría sufren la llamada relajación sin radiación que les permite regresar a su estado electrónico básico pero con una cantidad sustancial de energía vibratoria interna. Es decir, estas moléculas se vuelven vibracionalmente muy calientes. Posteriormente, estas moléculas calientes, a medida que experimentan transiciones de niveles vibratorios de alta energía a niveles de energía más bajos, emiten fotones infrarrojos (IR).
Si nuestra atmósfera estuviera desprovista de vapor de agua y\(CO_2\), estos fotones IR viajarían a través de la atmósfera y se perderían en el espacio. El resultado sería que gran parte de la energía proporcionada por los fotones visibles y ultravioleta del sol se perdería a través de la emisión IR. Sin embargo, el vapor de agua y\(CO_2\) no permiten que se escape tanta radiación IR. Estos gases de efecto invernadero absorben los fotones IR emitidos para generar agua vibracionalmente caliente y\(CO_2\) moléculas en la atmósfera. Estas moléculas excitadas vibracionalmente sufren colisiones con otras moléculas en la atmósfera y en la superficie terrestre. En tales colisiones, parte de su energía vibratoria puede transferirse a la energía cinética traslacional de las moléculas del compañero de colisión. De esta manera, la temperatura (que es medida de la energía traslacional promedio) aumenta. Por supuesto, las moléculas vibracionalmente calientes también pueden reemitir sus fotones IR, pero hay una capa gruesa de tales moléculas formando una manta alrededor de la tierra, y todas estas moléculas están disponibles para absorber y reemitir continuamente la energía IR. De esta manera, la manta evita que la radiación IR se escape y así mantiene nuestro ambiente cálido. Quienes vivimos en climas secos desérticos somos muy conscientes de tales efectos. Las noches claras y sin nubes en el desierto pueden volverse muy frías, principalmente porque gran parte de la producción de energía IR del día se pierde a causa de la emisión radiativa a través de la atmósfera y al espacio. Ahora aprendamos más sobre las vibraciones moleculares, cómo las excita la radiación IR y qué teoría tiene que ver con esto.
Cuando se utiliza radiación infrarroja (IR) para excitar una molécula, son las vibraciones de la molécula las que están en resonancia con el campo eléctrico oscilante\(\textbf{E} \cos(\omega t)\). Las moléculas que tienen momentos dipolares que varían a medida que ocurren sus vibraciones interactúan con el campo eléctrico IR a través de una energía potencial de la forma\(V = (\partial \boldsymbol{\mu}/\partial Q)\bullet\textbf{E} \cos(\omega t)\). Aquí\(\partial \boldsymbol{\mu}/\partial Q\) denota el cambio en el momento dipolar de la molécula\(M\) asociado con el movimiento a lo largo del modo vibracional normal etiquetado\(Q\).
A medida que se escanea la radiación IR, entra en resonancia con diversas vibraciones de la molécula en estudio, y la radiación puede ser absorbida. Conocer las frecuencias a las que se absorbe la radiación proporciona el conocimiento de las separaciones de los niveles de energía vibratoria en la molécula. Las absorciones asociadas con las transiciones desde el nivel vibratorio más bajo hasta la primera palanca excitada se denominan transiciones fundamentales. Aquellos que conectan el nivel más bajo al segundo estado excitado se llaman transiciones de primer armónico. Las excitaciones desde niveles excitados hasta niveles aún más altos se denominan absorciones de banda caliente.
Las transiciones vibracionales fundamentales ocurren a frecuencias que caracterizan diversos grupos funcionales en moléculas (por ejemplo, estiramiento O-H, flexión H-N-H, estiramiento N-H, estiramiento C-C, etc.). Como tal, un espectro vibracional ofrece una huella importante que permite al químico inferir qué grupos funcionales están presentes en la molécula. Sin embargo, cuando la molécula contiene modos vibratorios blandos, a menudo es más difícil usar información sobre la frecuencia de absorción para extraer información cuantitativa sobre la superficie de energía de la molécula y su estructura de unión. Como fue el caso de los niveles rotacionales de tales moléculas flojas, el tratamiento preciso de los movimientos vibracionales de gran amplitud de tales especies sigue siendo un área de intenso interés de investigación dentro de la comunidad teórica.
En una molécula poliatómica con\(N\) átomos, hay muchos modos vibracionales. La energía vibratoria total de dicha molécula puede aproximarse como una suma de términos, uno para cada una de las vibraciones\(3N-6\) (o\(3N-5\) para una molécula lineal):
\[E(v_1 ... v_{3N-5\text{ or }6}) = \hbar\omega_j \big(v_j + \dfrac{1}{2}\big). \tag{5.2.1}\]
Aquí,\(\omega_j\) es la frecuencia armónica del\(j^{\rm th}\) modo y\(v_j\) es el número cuántico vibracional asociado a ese modo. Como discutimos en el Capítulo 3, las funciones de onda vibratoria son productos de funciones vibracionales armónicas para cada modo:
\[\psi = \prod_{j=1}^{3N-5\text{ or }6} \psi_{v_j} (x (j)),\tag{5.2.1}\]
y los espaciamientos entre los niveles de energía en los que uno de los números cuánticos de modo normal aumenta por unidad se expresan como
\[\Delta E_{v_j} = E(...v_{j+1} ...) - E (...v_j ...) = \hbar\omega_j.\]
Es decir, se predice que las separaciones entre niveles vibracionales sucesivos de un modo dado sean independientes del número cuántico v dentro de este modelo armónico como se muestra en la Figura 5.15.
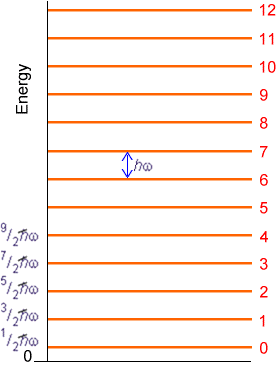
En el Capítulo 3, se presentan los detalles que conectan la curvatura local (es decir, los elementos de la matriz de Hesse) en la superficie de energía potencial de una molécula poliatómica con sus modos normales de vibración.
La evidencia experimental indica claramente que las desviaciones significativas de la expresión de energía del oscilador armónico ocurren a medida que\(v_j\) crece el número cuántico. Estas desviaciones se explican en términos del verdadero potencial de la molécula que se\(V(R)\) desvía fuertemente del\(\dfrac{1}{2}k (R-R_e)^2\) potencial armónico a mayor energía como se muestra en la Figura 5.16.
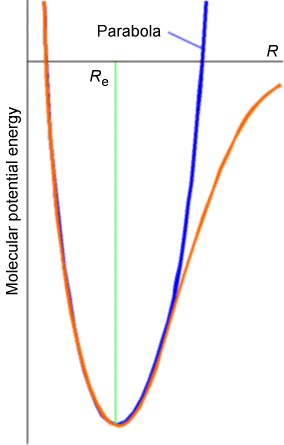
A longitudes de enlace más grandes, el verdadero potencial es más suave que el potencial armónico, y finalmente alcanza su asíntota, que se encuentra en la energía de disociación\(D_e\) por encima de su mínimo. Esta desviación de lo verdadero\(\dfrac{1}{2} k(R-R_e)^2\) hace que los verdaderos niveles\(V(R)\) de energía vibracional se encuentren por debajo de las predicciones armónicas.
Es convención expresar los niveles de energía vibratoria observados experimentalmente, a lo largo de cada uno de los modos\(3N-5\) o modos\(6\) independientes en términos de una fórmula anarmónica similar a lo que discutimos para el potencial Morse en el Capítulo 2:
\[E(v_j) = h\bigg[\omega_j \big(v_j + \dfrac{1}{2}\big) - (\omega_x)_j \big(v_j + \dfrac{1}{2}\big)^2 + (\omega_y)_j \big(v_j + \dfrac{1}{2}\big)^3 + (\omega_z)_j \big(v_j + \dfrac{1}{2}\big)^4 + ... \bigg]\]
El primer término es la expresión armónica. El siguiente se denomina la primera anarmonicidad; (generalmente) produce una contribución negativa a\(E(v_j)\) que varía a medida que\(\big(v_j + \dfrac{1}{2}\big)^2\). Los términos subsiguientes se denominan correcciones de mayor anarmonicidad. Las separaciones entre los niveles de\(v_j \rightarrow v_j + 1\) energía sucesivos vienen dadas entonces por:
\[\Delta{E}v_j = E(v_j + 1) - E(v_j)\tag{5.2.1}\]
\[= \hbar [\omega_j - 2(\omega_x)_j (v_j + 1) + ...]\tag{5.2.1}\]
Una gráfica del espaciamiento entre los niveles de energía vecinos versus\(v_j\) debe ser lineal para valores de\(v_j\) donde dominan los términos armónicos y de primera anarmónica. La pendiente de
se espera que tal trama sea\(-2\hbar(\omega_x)_j\) y la pequeña\(-v_j\) intercepción debería serlo\(\hbar[\omega_j - 2(\omega_x)_j]\). Dicha gráfica de datos experimentales, que claramente pueden ser utilizados para determinar los\((\omega_x)_j\) parámetros\(\omega_j\) y del modo vibracional de estudio, se muestra en la Figura 5.17.
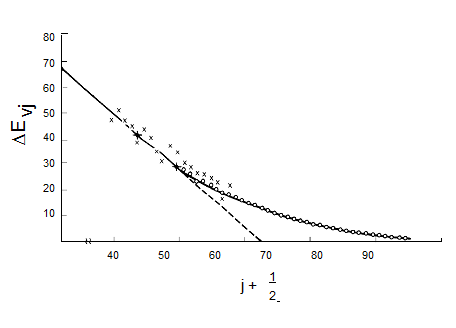
Figura 5.17 Gráfica Birge-Sponer de espaciamientos de energía vibratoria vs. número cuántico.
Estas llamadas gráficas Birge-Sponer también se pueden utilizar para determinar las energías de disociación de las moléculas si la vibración cuyos espaciamientos se trazan corresponde a un modo de estiramiento de enlace. Al extrapolar linealmente dicha gráfica de\(\Delta E_{v_j}\) valores experimentales a\(v_j\) valores grandes, se puede encontrar el valor\(v_j\) en el que el espaciamiento entre los niveles vibracionales vecinos va a cero. Este valor\(v_j\), max especifica el número cuántico del último nivel vibratorio límite para el modo particular de estiramiento de enlace de interés. La energía de disociación se\(D_e\) puede calcular añadiendo a\(\dfrac{1}{2}\hbar\omega_j\) (la energía del punto cero a lo largo de este modo) la suma de las separaciones entre los niveles de energía vibratoria vecinos de\(v_j = 0\) a\(v_j = v_{j, max}\):
\[D_e = \dfrac{1}{2}\hbar\omega_j + \sum_{v_j=0}^{v_{j,max}}\Delta D_{v_j}.\]
Entonces, en el caso de la espectroscopia vibracional, la teoría nos permite
- interpretar las líneas infrarrojas observadas en términos de absorciones que surgen en grupos funcionales localizados;
- extraer energías de disociación si se observa una larga progresión de líneas en una transición de estiramiento de enlace;
- y tratar vibraciones floppy altamente no armónicas mediante la realización de simulaciones dinámicas en una superficie de energía Born-Oppenheimer.
Cristalografía de Rayos X
En experimentos de cristalografía de rayos X, se emplean muestras cristalinas de las moléculas de interés y se utilizan los patrones de difracción producidos por los rayos X dispersos para determinar las posiciones de los átomos en la molécula entre sí utilizando la famosa fórmula de Bragg:
\[n\lambda = 2d \sin \theta .\tag{5.2.1}\]
En esta ecuación,\(\lambda\) es la longitud de onda de los rayos X,\(d\) es un espaciamiento entre capas (planos) de átomos en el cristal,\(q\) es el ángulo a través del cual se dispersa el haz de rayos X, y\(n\) es un entero (1,2,...) que etiqueta el orden del haz disperso.
Debido a que los rayos X se dispersan más fuertemente desde los electrones de la capa interna de cada átomo, las distancias interatómicas obtenidas de tales experimentos de difracción son, más precisamente, medidas de distancias entre altas densidades de electrones en los vecindarios de diversos átomos. Los rayos X interactúan más fuertemente con los electrones de la capa interna porque son estos electrones cuyas frecuencias de movimiento características de Bohr están (casi) en resonancia con la alta frecuencia de dicha radiación. Por esta razón, los rayos X pueden verse como dispersos desde los electrones centrales que residen cerca de los centros nucleares dentro de una molécula. Por lo tanto, los datos de difracción de rayos X ofrecen una forma muy precisa y confiable de sondear distancias interatómicas en moléculas
Las principales dificultades con las mediciones de rayos X son:
- Que uno necesita tener muestras cristalinas (a menudo, los materiales simplemente no se pueden cultivar como cristales),
- Que uno aprende sobre los espaciamientos interatómicos tal como ocurren en el estado cristalino, no como existen, por ejemplo, en solución o en muestras en fase gaseosa. Esto es especialmente problemático para los sistemas biológicos donde uno quisiera conocer la estructura de la biomolécula tal como existe dentro del organismo vivo.
Sin embargo, los datos de difracción de rayos X y su interpretación a través de la fórmula de Bragg proporcionan una de las formas más utilizadas y confiables para sondear la estructura molecular.
Espectroscopía de RMN
La espectroscopia de RMN sondea la absorción de radiación de radiofrecuencia (RF) por los espines nucleares de la molécula. Los espines que ocurren con mayor frecuencia en las muestras naturales son\(^1H\)\(^2H\) (protones), (deuterones)\(^{13}C\) y\(^{15}N\) núcleos. En presencia de un campo magnético externo\(B_{0z}\) a lo largo del\(z\) eje, cada núcleo tiene sus estados de espín divididos en energía por una cantidad dada por\(B_0(1-\sigma_k)\gamma_k M_I\), donde\(M_I\) está el componente del momento angular de\(k^{\rm th}\) espín del núcleo a lo largo del\(z\) eje,\(B_0\) es el fuerza del campo magnético externo, y\(\gamma_k\) es un llamado factor giromagnético (es decir, una constante) que es característico del\(k^{\rm th}\) núcleo. Esta división de los niveles de espín magnético por un campo magnético se denomina efecto Zeeman, y se ilustra en la Figura 5.18.
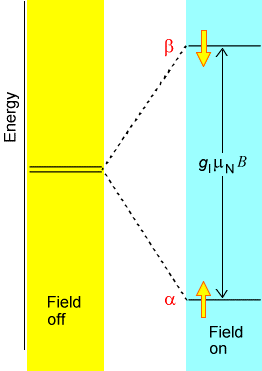
El factor\((1-\sigma_k)\) se introduce para describir el cribado del\(B_0\) campo externo en el\(k^{\rm th}\) núcleo causado por la nube de electrones que rodea este núcleo. En efecto,\(B_0(1-\sigma_k)\) es el campo magnético experimentado local al\(k^{\rm th}\) núcleo. Es este\((1-\sigma_k)\) cribado el que da lugar al fenómeno de los desplazamientos químicos en la espectroscopia de RMN, y es este factor el que permite que las mediciones de RMN de los factores de blindaje (\(\sigma_k\)) se relacionen, por teoría, con el entorno electrónico de un núcleo. En la Figura 5.19 se muestran los desplazamientos químicos de protones y\(^{13}C\) núcleos en una variedad de entornos de unión química.
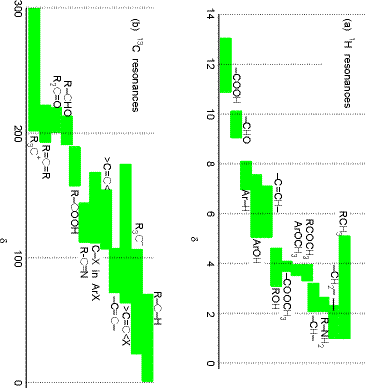
Debido a que el número\(M_I\) cuántico cambia en pasos de unidad y porque cada fotón posee una unidad de momento angular, la energía de RF\(\hbar\omega\) que estará en resonancia con los niveles divididos de Zeeman del\(k^{\rm th}\) núcleo viene dada por\(\hbar\omega = B_0(1-\sigma_k)\gamma_k\).
En la mayoría de los experimentos de RMN, se emplea una frecuencia de RF fija y se escanea el campo magnético externo hasta que se cumple la condición de resonancia anterior. Determinar a qué\(B_0\) valor un núcleo determinado absorbe la radiación RF permite determinar el blindaje local\((1-\sigma_k)\) para ese núcleo. Esto, a su vez, proporciona información sobre el entorno electrónico local a ese núcleo como se ilustra en la figura anterior. Estos datos le dicen mucho al químico sobre la estructura de la molécula porque sugieren qué tipos de grupos funcionales ocurren dentro de la molécula.
Para extraer aún más información geométrica de los experimentos de RMN, se hace uso de otra característica de los estados de espín nuclear. En particular, se sabe que los niveles de energía de un núcleo dado (por ejemplo, el\(k^{\rm th}\) uno) se ven alterados por la presencia de otros espines nucleares cercanos. Estas interacciones de acoplamiento espín-espín dan lugar a divisiones en los niveles de energía del\(k^{\rm th}\) núcleo que alteran la expresión de energía anterior de la siguiente manera:
\[E_M = B_0(1-\sigma_k)\gamma_k M+J_{M \, M’}\tag{5.2.1}\]
Donde\(M\) está el\(z\) -componente del momento angular de espín\(k^{\rm th}\) nuclear,\(M’\) es el componente correspondiente de un núcleo cercano que causa la división, y\(J\) se llama la constante de acoplamiento espín-espín entre los dos núcleos.
Ejemplos de cómo los espines en los centros vecinos dividen las líneas de absorción de RMN de un núcleo dado se muestran en las figuras 5.20-5.22 para tres casos comunes. El primero involucra un núcleo (etiquetado A) que está lo suficientemente cerca de otro núcleo magnéticamente activo (marcado X); el segundo involucra un núcleo (A) que está cerca de dos núcleos equivalentes (2X); y el tercero describe un núcleo (A) cercano a tres núcleos equivalentes (X3).
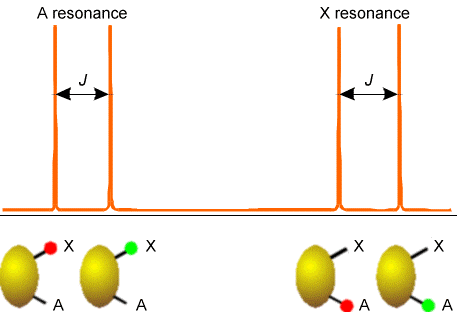
En la Figura 5.20 se ilustra la división en la absorción del núcleo X debido a la presencia de un solo núcleo vecino A (derecha) y la división en la absorción del núcleo A (izquierda) causada por el núcleo X. En ambos ejemplos, los núcleos X y A tienen sólo dos\(M_I\) valores, por lo que deben ser núcleos espin-1/2. Este tipo de patrón de división surgiría, por ejemplo, para un\(^{13}C-H\) grupo en la molécula de benceno donde A =\(^{13}C\) y X =\(^1H\).
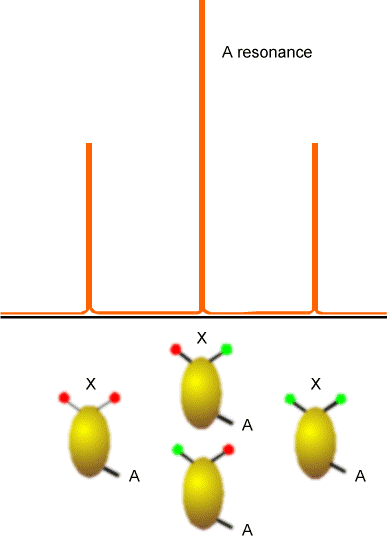
El patrón de división (\(AX_2\)) mostrado si la Figura 5.21 surgiría, por ejemplo, en el\(^{13}C\) espectro de un\(–CH_2^-\) grupo, e ilustra la división de la línea de absorción del núcleo A por los cuatro estados de espín que pueden ocupar los dos espines X equivalentes. Nuevamente, las líneas mostradas serían consistentes con X y A teniendo ambas spin 1/2 porque cada una asume solo dos\(M_I\) valores.
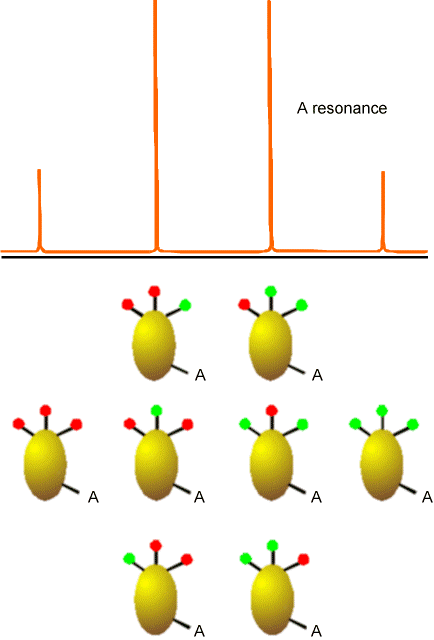
En la Figura 5.22 se encuentra el tipo de patrón de división (\(AX_3\)) que se aplicaría a las absorciones de\(^{13}C\) RMN para un\(–CH_3\) grupo. En este caso, la línea spin-1/2 A se divide por los ocho estados de espín que pueden ocupar los tres núcleos equivalentes de espín-1/2 H.
Las magnitudes de estas constantes de\(J\) acoplamiento dependen de las distancias R entre los dos núcleos a la sexta potencia inversa (es decir, as\(R^{-6}\)). También dependen de los\(g\) valores de los dos núcleos que interactúan. En presencia de división causada por núcleos cercanos (generalmente unidos covalentemente), el espectro de RMN de una molécula consiste en conjuntos de absorciones (cada una perteneciente a un tipo nuclear específico en un ambiente químico particular y por lo tanto tienen un desplazamiento químico específico) que se dividen por sus acoplamientos al otro núcleos. Debido a la fuerte decadencia del acoplamiento espín-espín con la distancia internuclear, la magnitud y el patrón de la división inducida en un núcleo por sus vecinos proporciona una clara firma de lo que son los núcleos vecinos (es decir, a través del número de\(M’\) valores asociados con el patrón de picos) y cómo lejos están estos núcleos (a través de la magnitud de la\(J\) constante, sabiendo que es proporcional a\(R^{-6}\)). Estos datos de vecinos cercanos, combinados con los datos del grupo funcional de desplazamiento químico, ofrecen información poderosa sobre la estructura molecular.
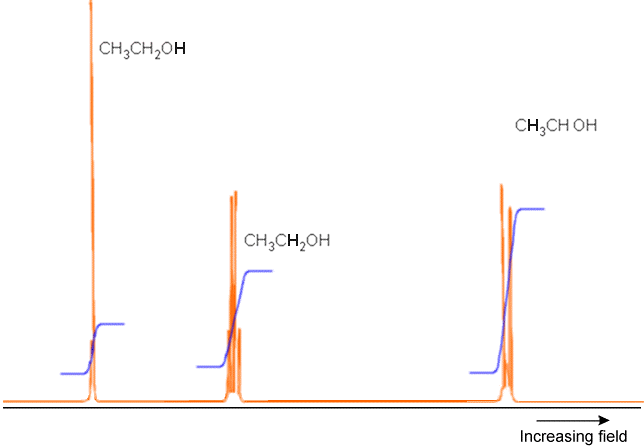
Un ejemplo de un espectro completo de RMN se da en la Figura 5.23 donde el\(^1H\) espectro (es decir, solo se muestran las absorciones de protones) de\(H_3C-H_2C-OH\) aparece junto con gráficas de las intensidades integradas bajo cada conjunto de picos. Estos últimos datos sugieren el número total de núcleos correspondientes a ese grupo de picos. Observe cómo la absorción del\(OH\) protón, la absorción de los dos protones equivalentes en el\(–CH_2^-\) grupo y la de los tres protones equivalentes en el\(–CH_3\) grupo ocurren a diferentes intensidades de campo (es decir, tienen diferentes cambios químicos). También tenga en cuenta cómo el\(OH\) pico se divide sólo ligeramente porque este protón está distante de cualquier otro, pero el pico de\(CH_3\) protones es dividido por los protones del\(–CH_2^-\) grupo vecino en un\(AX_2\) patrón. Finalmente, el pico\(–CH_2^-\) de los protones se divide por los tres protones del\(–CH_3\) grupo vecino (en un\(AX_3\) patrón).
En resumen, la espectroscopia de RMN es una herramienta muy poderosa que:
- nos permite extraer distancias internucleares (o al menos decir cuántos núcleos vecinos cercanos hay) y así información geométrica midiendo las constantes de acoplamiento\(J\) y posteriormente utilizando las expresiones teóricas que relacionan\(J\) valores con\(R^{-6}\) valores.
- nos permite sondear el entorno electrónico local de los núcleos dentro de las moléculas midiendo los desplazamientos químicos o blindaje\(\sigma_I\) y luego usando las ecuaciones teóricas que relacionan las dos cantidades. El conocimiento sobre el entorno electrónico le dice a uno, por ejemplo, el grado de polaridad en los enlaces conectados a ese centro nuclear.
- nos dice, a través de los patrones de división asociados a diversos núcleos, el número y la naturaleza de los núcleos vecinos, proporcionando de nuevo una gran cantidad de información sobre la estructura molecular.
Simulación Teórica de Estructuras
Hemos visto cómo la espectroscopia de microondas, infrarrojos y RMN, así como los datos de difracción de rayos X, cuando se someten a una interpretación adecuada utilizando las ecuaciones teóricas apropiadas, pueden ser utilizados para obtener una gran cantidad de información estructural sobre una molécula. Como se discute en la Parte 1 de este texto, la teoría también se utiliza para sondear la estructura molecular de otra manera. Es decir, no sólo la teoría ofrece las ecuaciones que conectan los datos experimentales con las propiedades moleculares, sino que también permite simular una molécula. Esta simulación se realiza resolviendo la ecuación de Schrödinger para que los movimientos de los electrones generen una superficie de energía potencial\(E(R)\), después de lo cual se puede buscar en este paisaje energético puntos donde los gradientes a lo largo de todas las direcciones desaparezcan. Un ejemplo de tal PES se muestra en la Figura 5.24 para un caso simple en el que la energía depende solo de dos parámetros geométricos. Incluso en tal caso, se pueden encontrar varios mínimos locales y estructuras de estado de transición que los conectan.
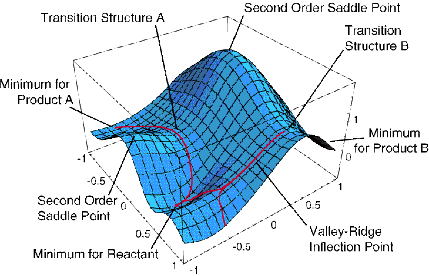
Como se discutió en el Capítulo 3, entre los puntos estacionarios en la superficie de energía potencial (PES), aquellos en los que todos los valores propios de la matriz de la segunda derivada (Hesse) son positivos representan isómeros geométricamente estables de la molécula. Aquellos puntos estacionarios en el PES en los que todos los valores propios de Hesse menos uno son positivos y uno negativo representan estructuras de estado de transición que conectan pares de isómeros estables.
Una vez que se han identificado los isómeros estables de una molécula que se encuentran dentro de algún intervalo de energía por encima del isómero más bajo, los movimientos vibracionales de la molécula dentro de la vecindad de cada uno de tales isómeros pueden describirse resolviendo la ecuación de Schrödinger para las funciones de onda vibratoria\(\chi_v(Q)\) perteneciente a cada modo normal o resolviendo las ecuaciones clásicas de Newton de movimiento usando el gradiente\(\dfrac{∂E}{∂Q}\) del PES para calcular las fuerzas a lo largo de cada dirección de distorsión molecular\(Q\):
\[F_Q = -\dfrac{\partial E}{\partial Q} \tag{5.2.1}\]
La decisión sobre si usar las ecuaciones de Schrödinger o Newtonian para tratar el movimiento vibracional depende de si se desea (necesita) incluir adecuadamente los efectos cuánticos (por ejemplo, movimiento de punto cero y patrones nodales de función de onda) en la simulación.
Una vez que se han descrito los movimientos vibracionales para un isómero particular, y dado el conocimiento de la geometría de ese isómero, se pueden evaluar los momentos de inercia, se puede promediar vibracionalmente adecuadamente todas las\(R^{-2}\) cantidades que entran en estos momentos, y, por lo tanto, se puede simular el microondas espectro de la molécula. Además, dada la matriz hessiana para este isómero, se puede formar su variante ponderada en masa cuyos valores propios distintos de cero dan las frecuencias armónicas de vibración de modo normal de ese isómero y cuyos vectores propios describen los movimientos atómicos que corresponden a estas vibraciones. Además, la solución de la ecuación electrónica de Schrödinger permite calcular los\(\sigma_I\) valores de blindaje de RMN en cada núcleo así como las constantes de acoplamiento espín-espín\(J\) entre pares de núcleos (el tratamiento de estos sujetos está más allá del nivel de este texto; lo puedes encontrar en Molecular Teoría de la Estructura Electrónica por Helgaker, et. al.). Nuevamente, usando el conocimiento del movimiento vibracional, uno puede promediar\(J\) los valores\(\sigma\) y sobre este movimiento para ganar promediado vibracionalmente\(\sigma_I\) y\(J_{I,I’}\) valores que simulen mejor los parámetros experimentales.
Se lleva a cabo tal simulación teórica de una molécula por diversas razones.
Especialmente en los primeros días del desarrollo de herramientas teóricas para resolver la ecuación electrónica de Schrödinger o el problema del movimiento vibracional, uno lo haría para moléculas cuyas estructuras y espectros IR y RMN eran bien conocidos. El propósito en tales casos fue calibrar la precisión de los métodos teóricos frente a los datos experimentales establecidos. Ahora que las herramientas teóricas han sido razonablemente bien probadas y se pueden confiar (dentro de límites conocidos de precisión), a menudo se utilizan propiedades estructurales y espectroscópicas teóricamente simuladas para identificar características espectrales cuyo origen molecular no se conoce. Es decir, se comparan los espectros teóricos de una variedad de moléculas de prueba con las características espectrales observadas para intentar identificar la molécula que produjo los espectros.
También es común el uso de simulaciones para examinar especies que son especialmente difíciles de generar en cantidades razonables en el laboratorio y especies que no persisten por largos tiempos. Los radicales reactivos, cationes y aniones suelen ser difíciles de generar en el laboratorio y pueden ser imposibles de retener en concentraciones suficientes y durante una duración suficiente para permitir la caracterización experimental. En tales casos, la simulación teórica de las propiedades de estas moléculas puede ser la forma más confiable de acceder a dichos datos. Además, se podrían utilizar simulaciones para examinar el comportamiento de las moléculas en condiciones extremas como alta presión, confinamiento a espacios nanoscópicos, altas temperaturas o temperaturas muy bajas para las cuales los experimentos podrían ser muy difíciles o costosos de llevar a cabo.
Déjame contarte sobre un ejemplo de cómo tal simulación teórica ha demostrado ser útil, probablemente incluso esencial, para interpretar datos experimentales (los datos se reportan en N. I. Hammer, J-W. Shin, J. M. Headrick, E. G. Diken, J. R. Roscioli, G. H. Weddle, y M. A. Johnson, Science 306, 675 (2004)). En el grupo del Prof. Mark Johnson en Yale, se realiza espectroscopía infrarroja sobre iones en fase gaseosa. En este experimento en particular, se formaron aniones de racimo de agua\(Ar_k(H_2O)_n^-\) con uno o más átomos de Ar unidos a ellos y, utilizando un espectrómetro de masas, se seleccionaron los iones de una masa específica para su posterior estudio. En el ejemplo aquí ilustrado, se estudió el cúmulo\(Ar_k(H_2O)_4^-\) que contenía cuatro moléculas de agua.
Cuando la radiación infrarroja (IR) incide sobre los\(Ar_k(H_2O)_4^-\) iones, puede ser absorbida si su frecuencia coincide con la frecuencia de uno de los modos vibracionales de este cúmulo. Si, por ejemplo, se absorbe radiación IR en el rango de frecuencias de 1500-1700 cm -1 (este rango corresponde a frecuencias de vibraciones de flexión H-O-H), este exceso de energía interna puede provocar que uno o más de los átomos de Ar débilmente unidos sean expulsados del\(Ar_k(H_2O)_4^-\) grupo, disminuyendo así el número de\(Ar_k(H_2O)_4^-\) iones intactos en el espectrómetro de masas. La disminución en el número de iones intactos es una medida directa entonces de la absorción de la luz IR. Al monitorear el número de\(Ar_k(H_2O)_4^-\) (es decir, la intensidad de la señal del espectrómetro de masas en esta relación masa/carga particular) a medida que la radiación IR se sintoniza a través del rango de frecuencias de 1500-1700 cm -1, los experimentalistas obtienen firmas espectrales (es decir, la pérdida de intensidad de iones) del IR. absorción por los iones del\(Ar_k(H_2O)_4^-\) racimo.
Al realizar este tipo de experimentos utilizando\(Ar_5(H_2O)_4^-\) y escaneando la radiación IR en el rango de frecuencias 1500-1700 cm -1, obtuvieron el espectro etiquetado A en la Figura 5. 24 a. cuando realizaron el mismo tipo de experimento\(Ar_{10}(D_2O)_4^-\) y escanearon en el 2400-2800 cm -1 rango de frecuencias (que es donde se sabe que ocurren las vibraciones de estiramiento O-D), obtuvieron el espectro etiquetado B en la Figura 5. 24 a.
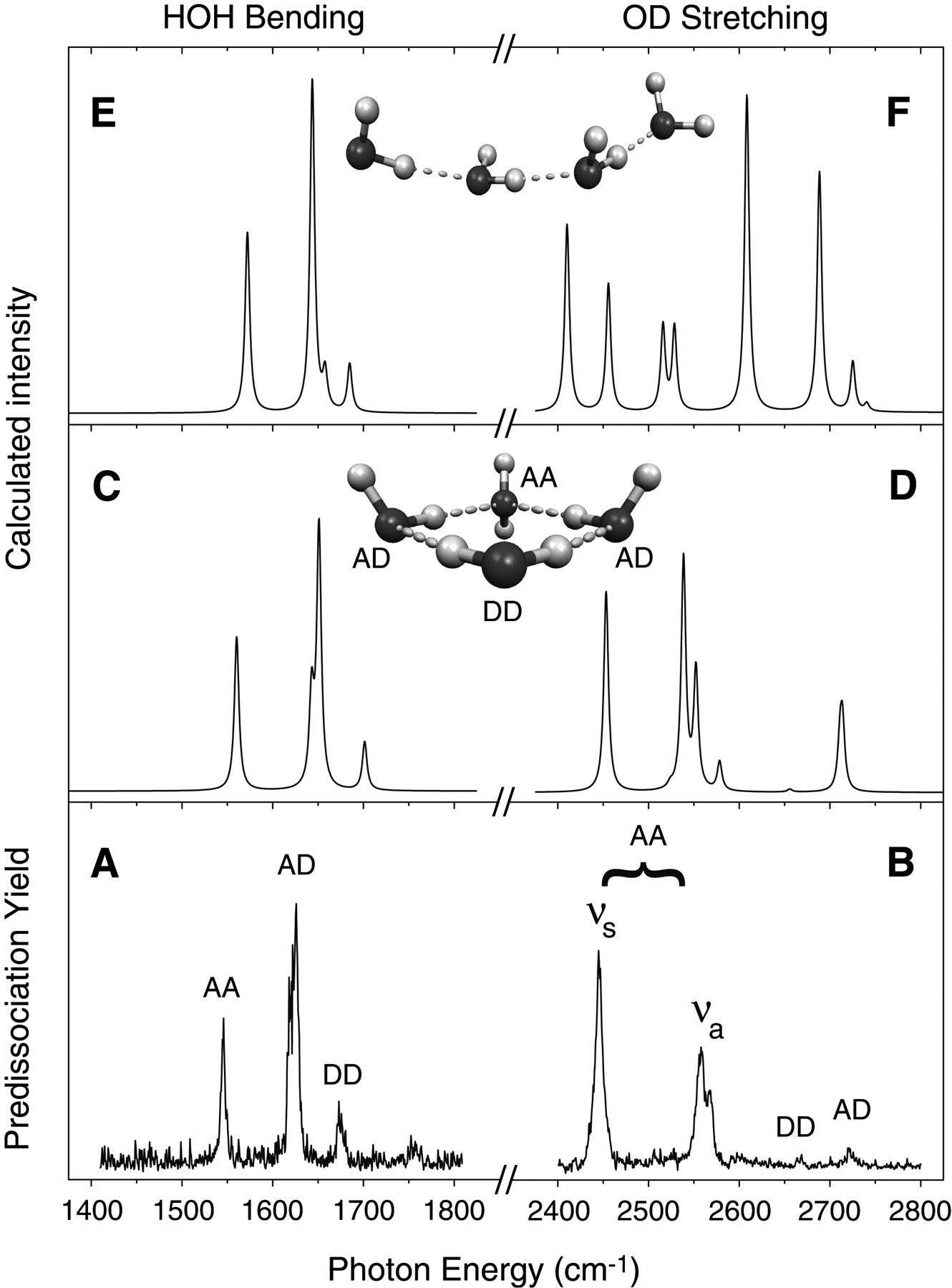
Lo que los experimentalistas no sabían, sin embargo, es cuál era la estructura geométrica del\((H_2O)_4^-\) ion subyacente. Tampoco sabían exactamente qué vibraciones de flexión H-O-H u O-H (u O-D) de estiramiento estaban causando los diversos picos mostrados en la Figura 5.24 a A y B.
Al realizar cálculos de estructura electrónica en un gran número de geometrías para\((H_2O)_4^-\) y buscar mínimos locales en el estado electrónico de este ion (hay un número muy grande de dichos mínimos locales) y luego usar la matriz de Hessian ponderada en masa en cada mínimo local para calcular el las energías vibracionales de structure, los experimentalistas fueron capaces de averiguar para qué estructura\((H_2O)_4^-\) era más consistente con su espectro IR observado. Por ejemplo, para la estructura bastante extendida de\((H_2O)_4\), computaron el espectro IR mostrado en el panel E (y para\((D_2O)_4^-\) en el panel F) de la Figura 5. 24 a. Alternativamente, para la estructura cíclica de\((H_2O)_4\) -, computaron el espectro IR mostrado en el panel C (y para\((D_2O)_4^-\) en el panel D) de la Figura 5. 24 a. Claramente, el espectro de los paneles C y D concuerda mucho mejor con su espectro experimental en los paneles A y B que el espectro de los paneles E y F. Con base en estas comparaciones, estos científicos concluyeron que los\((H_2O)_4^-\) iones en su\(Ar_5(H_2O)_4^-\) y\(Ar_{10}(D_2O)_4^-\) tienen la geometría cíclica, no la geometría cuasilineal extendida. Además, al observar qué modos vibratorios particulares del cíclico\((H_2O)_4^-\) produjeron qué picos en los paneles C y D, pudieron asignar cada uno de los picos IR vistos en sus datos de los paneles A y B. Este es un buen ejemplo de cómo la simulación teórica puede ayudar a interpretar datos experimentales; sin el teoría, estos científicos no conocerían la geometría de\((H_2O)_4^-\).
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


