6.1: Tratamiento Teórico de la Estructura Electrónica

En el capítulo 5, te presenté las estrategias que la teoría utiliza para interpretar datos experimentales relacionados con tales materias, y cómo y por qué la teoría también puede ser utilizada para simular el comportamiento de las moléculas. En la realización de simulaciones, la energía\(E(R)\) electrónica Born-Oppenheimer en función de las\(3N\) coordenadas de los\(N\) átomos en la molécula juega un papel central. Es en este paisaje donde se buscan isómeros estables y estados de transición, y es la segunda matriz derivada (hessiana) de esta función la que proporciona las frecuencias vibracionales armónicas de dichos isómeros. En el presente Capítulo, quiero brindarles una introducción a las herramientas que utilizamos para resolver la ecuación electrónica de Schrödinger a generar\(E(R)\) y la función de onda electrónica\(\psi(r|R)\). En esencia, este tratamiento se centrará en orbitales de átomos y moléculas y cómo los obtenemos e interpretamos.

Para un átomo, se pueden aproximar los orbitales utilizando las soluciones de la ecuación hidrogénica de Schrödinger discutida en la Parte 1 de este texto. Aunque tales funciones no son soluciones adecuadas a la ecuación real de Schrödinger de\(N\) electrones (lo creas o no, nadie ha resuelto nunca exactamente ninguna ecuación de este tipo para\(N > 1\)) de ningún átomo, pueden usarse como perturbación o aproximaciones variacionales del punto de partida cuando uno puede estar satisfecho con respuestas cualitativamente precisas. En particular, las soluciones de este problema hidrogénico de un electrón forman la base cualitativa de gran parte de la teoría orbital atómica y molecular. Como se discute en detalle en la Parte 1, estos orbitales están etiquetados por\(n\)\(l\), y números\(m\) cuánticos para los estados unidos y por\(l\) y números\(m\) cuánticos y la energía\(E\) para los estados continuos.

Por mucho que los orbitales de partículas en una caja se utilizan para describir cualitativamente\(\pi\) electrones en polienos conjugados o bandas electrónicas en sólidos, estos llamados orbitales similares a hidrógeno proporcionan descripciones cualitativas de orbitales de átomos con más de un solo electrón. Al introducir el concepto de cribado como una forma de representar las interacciones repulsivas entre los electrones de un átomo, se\(Z_{\rm eff}\) puede utilizar una carga nuclear efectiva en lugar de\(Z\) en las\(E_{n,l}\) fórmulas hidrogénicas\(\psi_{n,l,m}\) y para generar orbitales atómicos aproximados para ser llenados por electrones en un átomo de muchos electrones. Por ejemplo, en la aproximación más cruda de un átomo de carbono, los dos\(1s\) electrones experimentan la atracción nuclear completa así\(Z_{\rm eff} =6\) para ellos, mientras que los\(2p\) electrones\(2s\) y son proyectados por los dos\(1s\) electrones, así\(Z_{\rm eff}= 4\) para ellos. Dentro de esta aproximación, uno ocupa entonces dos\(1s\) orbitales con\(Z=6\), dos\(2s\) orbitales con\(Z=4\) y dos\(2p\) orbitales con\(Z=4\) en la formación de la función de onda de producto de seis electrones completa del estado de carbono de menor energía

\[\psi(1, 2, …, 6) = \psi_{1s} \alpha(1) \psi_{1s} \alpha(2) \psi_{2s} \alpha(3) … \psi_{1p}(0) \beta(6). \]

Sin embargo, dichos orbitales aproximados no son suficientemente precisos para ser útiles en simulaciones cuantitativas de estructura atómica y molecular. En particular, sus energías no siguen adecuadamente las tendencias en las energías orbitales atómicas (AO) que se enseñan en las clases introductorias de química y que se muestran pictóricamente en la Figura 6.1.

Figura 6.1.1: Energías de Orbitales Atómicos como Funciones de Carga Nuclear para Átomos Neutros.

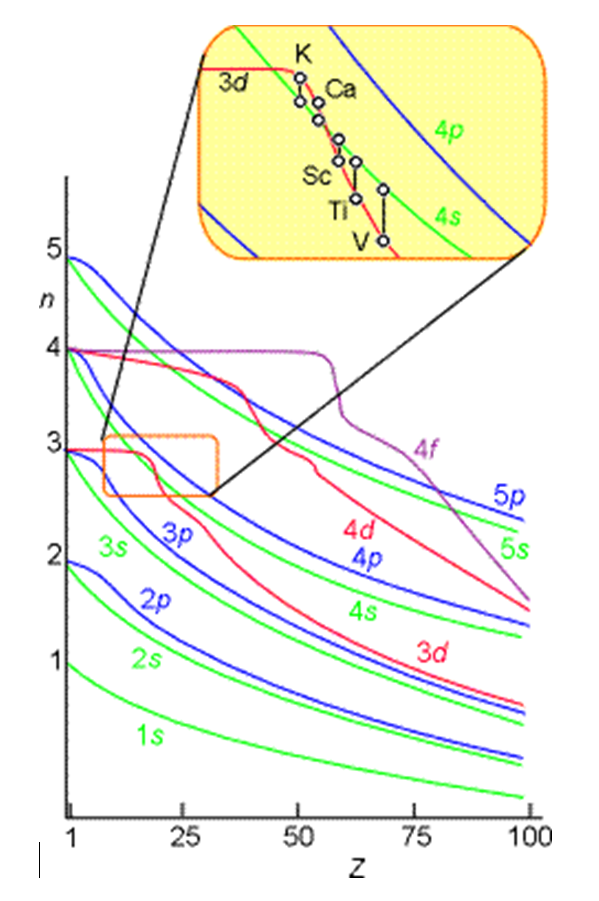
Por ejemplo, las energías relativas de los\(4s\) orbitales\(3d\) y no se describen adecuadamente en un modelo que trata los efectos de repulsión de electrones en términos de un simple factor de cribado. Entonces, ahora es el momento de examinar cómo podemos ir más allá del modelo de cribado y tomar en cuenta de una manera más confiable los efectos de repulsión de electrones, que provocan que los acoplamientos interelectrónicos que hacen insoluble la ecuación de Schrödinger.

Unidades atómicas

El hamiltoniano electrónico que aparece a lo largo de este texto se expresa comúnmente en la literatura y en otros textos en las llamadas unidades atómicas (aus). En esa forma, se escribe de la siguiente manera:

\[H_e = \sum_j \left[ -\frac{1}{2} \nabla_j^2 - \sum_a \frac{Z_a}{r_{j,a}} \right] + \sum_{j< k} \frac{1}{r_{j,k}} .\]

Se introducen unidades atómicas para eliminar todos los factores h, e y yo de la ecuación de Schrödinger.

Para efectuar la transformación unitaria que da como resultado que el hamiltoniano aparezca como arriba, se observa que el operador de energía cinética escala como\(r_j^{-2}\) mientras que los potenciales de Coulomb escalan como\(r_j^{-1}\) y como\(r_{j,k}^{-1}\). Entonces, si cada una de las coordenadas cartesianas de los electrones y núcleos se expresara como una unidad de longitud\(a_0\) multiplicada por un factor de longitud adimensional, el operador de energía cinética implicaría términos de la forma

\(( - \hbar^2/2(a_0)^2m_e ) \nabla_j^2\), y los potenciales de Coulomb aparecerían como\(Z_ae^2/(a_0)r_{j,a}\) y\(e^2/(a_0)r_{j,k}\), con los\(r_{j,k}\) factores\(r_{j,a}\) y ahora refiriéndose a las coordenadas adimensionales. Un factor de\(e^2/a_0\) (que tiene unidades de energía ya que a_0 tiene unidades de longitud) puede entonces eliminarse de las energías Coulomb y cinética, después de lo cual los términos de energía cinética aparecen como\(( - \hbar^2/2(e^2a_0)m_e ) \nabla_j^2\) y las energías potenciales aparecen como\(Z_a/r_{j,a}\) y\(1/r_{j,k}\). Entonces, elegir\(a_0 = \hbar^2/e^2m_e\) cambia los términos de energía cinética en\(-1/2 \nabla_j^2\); como resultado, todo el Hamiltoniano electrónico toma la forma dada anteriormente en la que no\(e^2\), yo, o\(\hbar^2\) factores aparecen. El valor del llamado radio de Bohr\(a_0 = \hbar^2/e^2m_e\) resulta ser 0.529 Å, y la llamada unidad de energía Hartree\(e^2/a_0\), que factoriza fuera de He, es 27.21 eV o 627.51 kcal/mol.

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

• Integrated by Tomoyuki Hayashi (UC Davis)