6.2: Orbitales

Hartree Descripción

Se supone que las energías y funciones de onda dentro de las teorías más utilizadas de la estructura atómica surgen como soluciones de una ecuación de Schrödinger cuyo hamiltoniano\(h_e(r)\) posee tres tipos de energías:

1. Energía cinética, cuyo valor promedio se calcula tomando el valor esperado del operador de energía cinética\(-\dfrac{\hbar^2}{2m} \nabla^2\) con respecto a cualquier solución particular\(\phi_j(r)\) a la ecuación de Schrödinger:\[KE = \langle\phi_j| -\dfrac{\hbar^2}{2m} \nabla^2 |\phi_j\rangle \]
2. Energía de atracción coulómbica con el núcleo de carga\(Z\):\[\langle\phi_j| -\dfrac{Z_e^2}{r} |\phi_j\rangle\]
3. Energías de repulsión de Coulomb con todos los\(N-1\) demás electrones, que se supone que ocupan otros orbitales atómicos (AO) denotados\(\phi_K\), con esta energía calculada como

\[\sum_K \langle\phi_j(r) \phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle.\label{6.1.2}\]

La notación Dirac\(\langle\phi_j(r) \phi_K(r’) |\dfrac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle\) se utiliza para representar la integral de Coulomb de seis dimensiones

\[J_{J,K} = \int |\phi_j(r)|^2 |\phi_K(r’)|^2 \dfrac{e^2}{r-r'} dr dr’ \label{6.1.3}\]

que describe la repulsión de Coulomb entre la densidad de carga\(|\phi_j(r)|^2\) para el electrón adentro\(\phi_j\) y la densidad de carga\(|\phi_K(r’)|^2\) para el electrón adentro\(\phi_K\). Por supuesto, la suma sobre\(K\) debe limitarse\(K=J\) a excluir para evitar contar una “autointeracción” del electrón en orbital\(\phi_j\) consigo mismo.

La energía total\(\epsilon_J\) de la órbita\(\phi_j\), es la suma de las tres contribuciones anteriores:

\[\epsilon_J = \langle\phi_j| - \frac{\hbar^2}{2m} \nabla^2 |\phi_j\rangle + \langle\phi_j| -\frac{Z_e^2}{r} |\phi_j\rangle + \sum_K \langle\phi_j(r) \phi_K(r’) |\frac{e^2}{|r-r’|} | \phi_j(r) \phi_K(r’)\rangle.\label{6.1.4}\]

Este tratamiento de los electrones y sus orbitales se conoce como el nivel Hartree de la teoría. Como se indicó anteriormente, cuando se utilizan AO hidrogénicos cribados para aproximar los\(\phi_K\) orbitales\(\phi_j\) y, los\(\epsilon_J\) valores resultantes no producen predicciones precisas. Por ejemplo, el negativo de\(\epsilon_J\) debe aproximarse a la energía de ionización para la eliminación de un electrón del AO\(\phi_j\). Dichos potenciales de ionización (IP) se pueden medir, y los valores medidos no concuerdan bien con los valores teóricos cuando se realiza una aproximación de cribado crudo para los AO s.

LCAO-Expansión

Para mejorar el uso de AO hidrogénicos seleccionados, es más común aproximar cada uno de los AO de Hartree {\(\phi_K\)} como una combinación lineal de los llamados AO base {\(\chi_\mu\)}:

\[\phi_J = \sum_\mu C_{J,\mu} \chi_\mu.\label{6.1.5}\]

usando lo que se denomina expansión de combinación lineal de orbitales atómicos (LCAO). En esta ecuación, los coeficientes de expansión {\(C_{J,\mu}\)} son las variables que se van a determinar resolviendo la ecuación de Schrödinger

\[h_e \phi_J = \epsilon_J \phi_J. \label{6.1.6}\]

Después de sustituir la expansión LCAO por\(\phi_J\) en esta ecuación de Schrödinger, multiplicando a la izquierda por uno de los AO base\(\chi_\nu\), y luego integrándose sobre las coordenadas del electrón en\(\phi_J\), se obtiene

\[\sum_\mu \langle\chi_\nu| h_e| \chi_\mu\rangle C_{J,\mu} = \epsilon_J \sum_\mu \langle\chi_\nu| \chi_\mu\rangle C_{J,\mu} . \label{6.1.7}\]

Esta es una ecuación de valores propios de matriz en la que los\(\epsilon_J\) y {\(C_{J,\mu}\)} aparecen como valores propios y vectores propios. Las matrices\(\langle\chi_\nu| h_e| \chi_\mu\rangle\) y\(\langle\chi_\nu| \chi_\mu\rangle\) se denominan matrices hamiltonianas y superpuestas, respectivamente. Una expresión explícita para el primero se obtiene introduciendo la definición anterior de él:

\[\langle\chi_\nu| h_e| \chi_\mu\rangle = \langle\chi_\nu| - \frac{\hbar^2}{2m} \nabla^2 |\chi_\mu\rangle + \langle\chi_\nu| -\frac{Ze^2}{r} |\chi_\mu\rangle \label{6.1.8}\]

\[+ \sum_{\eta,\gamma} \sum_K C_{K,\eta} C_{K,\gamma} \langle\chi_\nu(r) \chi_\eta(r’) |\frac{e^2}{|r-r’|} | \chi_\mu(r) \chi_\gamma(r’)\rangle. \label{6.1.9}\]

Una cosa importante a tener en cuenta sobre la forma de las ecuaciones matriciales de Hartree es que para calcular la matriz hamiltoniana, hay que conocer los coeficientes LCAO {\(C_{K,\gamma}\)} de los orbitales que ocupan los electrones. Por otro lado, se supone que estos coeficientes LCAO se encuentran resolviendo las ecuaciones de valores propios de la matriz de Hartree. Esta paradoja lleva a la necesidad de resolver estas ecuaciones iterativamente en una técnica llamada de campo autoconsistente (SCF). En el proceso SCF, se introduce una aproximación inicial a los {\(C_{K,\gamma}\)} coeficientes. Esto permite entonces formar la matriz hamiltoniana definida anteriormente. Las ecuaciones de la matriz de Hartree

\[\sum_\mu \langle\chi_\nu| h_e| \chi_\mu\rangle C_{J,m} = \epsilon_J \sum_\mu \langle\chi_\nu| \chi_\mu\rangle C_{J,\mu} \label{6.1.10}\]

luego se resuelven para nuevos {\(C_{K,\gamma}\)} coeficientes y para las energías orbitales {\(\epsilon_K\)}. Los nuevos coeficientes LCAO de aquellos orbitales que están ocupados se utilizan entonces para formar una nueva matriz hamiltoniana, después de lo cual las ecuaciones de Hartree se resuelven nuevamente para otra generación de coeficientes LCAO y energías orbitales. Este proceso se continúa hasta que las energías orbitales y los coeficientes LCAO obtenidos en iteraciones sucesivas no difieran apreciablemente. Tras tal convergencia, se dice que se ha realizado un campo autoconsistente porque los {\(C_{K,\gamma}\)} coeficientes se utilizan para formar un potencial de campo de Coulomb que detalla las interacciones electrón-electrón.

Conjuntos de Bases

Orbitales tipo Slater y orbitales de tipo gaussiano

Como se señaló anteriormente, es posible utilizar los orbitales hidrogénicos tamizados como los {\(\chi_\mu\)}. Sin embargo, se ha dedicado mucho esfuerzo a desarrollar conjuntos alternativos de funciones para usar como orbitales de base. El resultado de este esfuerzo ha sido producir dos tipos de funciones que actualmente son ampliamente utilizadas. Los orbitales de base comúnmente utilizados en el proceso LCAO se agrupan en dos clases primarias:

1. Los orbitales tipo Slater (\[c_{n,l,m} (r,\theta,\phi) = N_{n,l,m,z} Y_{l,m} (\theta,\phi) r_{n-1} e^{-zr}\]STO) se caracterizan por números cuánticos\(n\)\(l\),\(m\) y y exponentes (que caracterizan el tamaño radial de la órbita)\(z\). El símbolo\(N_{n,l,m,z}\) denota la constante de normalización.
2. Los orbitales cartesianos de tipo gaussiano (GTO)\[c_{a,b,c} (r,\theta,\phi) = N'_{a,b,c,a} x_a y_b z_c e^{-ar^2}\] se caracterizan por números cuánticos\(a\)\(b\), y\(c\), que detallan la forma angular y la dirección de la órbita, y exponentes\(a\) que gobiernan el tamaño radial.

Para ambos tipos de AO, las coordenadas\(r\),\(\theta\), y\(\phi\) se refieren a la posición del electrón con respecto a un conjunto de ejes unidos al núcleo sobre el cual se ubica la base orbital. Tenga en cuenta que los orbitales tipo Slater (STO) son similares a los orbitales hidrogénicos en la región cercana al núcleo. Específicamente, tienen una pendiente distinta de cero cerca del núcleo

\[\dfrac{d}{dr}(e^{-zr})_{r=0} = -z.\]

En contraste, los GTO, tienen pendiente cero cerca\(r=0\) porque

\[\dfrac{d}{dr}(e^{-ar^2})_{r=0} = 0.\]

Decimos que los STO muestran una cúspide en la\(r=0\) que es característica de las soluciones hidrogénicas, mientras que los OGT no. Aunque las STO tienen el comportamiento adecuado de cúspide cerca de los núcleos, se utilizan principalmente para cálculos atómicos y de moléculas lineales porque las integrales multicéntricas

\[\langle\chi_\mu(1) \chi_\kappa(2)|\dfrac{e^2}{|r_1-r_2|}| \chi_\nu(1) \chi_\gamma(2)\rangle\label{6.1.11}\]

que surgen en los cálculos de moléculas poliatómicas (discutiremos estas integrales más adelante en este Capítulo) no pueden evaluarse eficientemente cuando se emplean STO. Por el contrario, tales integrales pueden calcularse rutinariamente cuando se usan GTO. Esta ventaja fundamental de los GTO ha llevado al dominio de estas funciones en la química cuántica molecular.

Para superar la debilidad primaria de las funciones GTO (es decir, sus derivadas radiales desaparecen en el núcleo), es común combinar dos, tres o más GTO, con coeficientes de combinación que son fijos y no tratados como parámetros LCAO, en nuevas funciones llamadas GTO contratados (CGTO). Típicamente, una serie de GTO radialmente apretados, medios y sueltos se multiplican por coeficientes de contracción y se suman para producir un CGTO que se aproxime a la cúspide apropiada en el centro nuclear (aunque ninguna combinación de GTO tal puede producir exactamente tal cúspide porque cada GTO tiene pendiente cero en\(r = 0\).

Aunque la mayoría de los cálculos sobre las moléculas se realizan ahora usando orbitales gaussianos, cabe señalar que se pueden usar otros conjuntos de bases siempre que abarquen lo suficiente de las regiones del espacio (radial y angular) donde reside una densidad de electrones significativa. De hecho, es posible utilizar orbitales de onda plana de la forma

\[\chi(r,\theta,\phi) = N\exp[i(k_x r \sin{\theta} \cos{\phi} + k_y r \sin_{\theta} \sin{\phi} + k_z r \cos{\theta})],\label{6.1.12}\]

donde\(N\) es una constante de normalización y\(k_x\),\(k_y\), y\(k_z\) son números cuánticos que detallan el momento o longitud de onda de la órbita a lo largo de las direcciones\(x\)\(y\),, y\(z\) cartesianas. La ventaja de usar orbitales tan simples es que las integrales que uno debe realizar son mucho más fáciles de manejar con tales funciones. La desventaja es que se deben usar muchas de esas funciones para describir con precisión distribuciones de carga con picos agudos de, por ejemplo, orbitales de núcleo de concha interna, conservando al mismo tiempo suficiente flexibilidad para describir también la densidad de electrones mucho más suave en las regiones de valencia. Se ha dedicado mucho esfuerzo a desarrollar y tabular en ubicaciones ampliamente disponibles conjuntos de orbitales de base STO o GTO para elementos del grupo principal y metales de transición. Este esfuerzo continuo está dirigido a proporcionar bibliotecas de conjunto de bases estándar que:

1. Rendimiento de precisión química predecible en las energías resultantes.
2. Son rentables de usar en cálculos prácticos.
3. Son relativamente transferibles para que la base de un átomo dado sea lo suficientemente flexible como para ser utilizada para ese átomo en diversos entornos de unión (por ejemplo, hibridación y grado de ionización).

Base Fundamental y Base de Valencia

Al construir una base orbital atómica, se puede elegir entre varias clases de funciones. Primero, se debe especificar el tamaño y la naturaleza del núcleo primario y la base de valencia. Dentro de esta categoría, son comunes las siguientes opciones:

1. Una base mínima en la que el número de orbitales CGTO es igual al número de orbitales atómicos de núcleo y valencia en el átomo.
2. Una base de doble zeta (DZ) en la que se utilizan el doble de CGTO que los orbitales atómicos de núcleo y valencia. El uso de más funciones básicas está motivado por el deseo de proporcionar flexibilidad variacional adicional para que el proceso LCAO pueda generar orbitales moleculares de difusión variable a medida que varía la electronegatividad local del átomo. Una base de doble zeta de valencia (VDZ) tiene solo un CGTO para representar los orbitales de capa interna, pero usa dos conjuntos de CGTO para describir los orbitales de valencia.
3. Una base triple zeta (TZ) en la que se utilizan tres veces más CGTO que el número de orbitales atómicos de núcleo y valencia (por supuesto, también hay bases cuádruple zeta y zeta superior). Además, existen bases VTZ que tratan los orbitales de concha interna con un CGTO y los orbitales de valencia con tres CGTO.

La optimización de los exponentes orbitales (z's o a's) y los coeficientes de contracción Gto-CGTO para el tipo de bases descritas anteriormente ha experimentado un crecimiento considerable en los últimos años. El grupo teórico de Pacific Northwest National Labs (PNNL) ofrece un sitio web mundial desde el cual se puede encontrar (e incluso descargar en una forma preparada para ingresar a cualquiera de varios códigos de estructura electrónica de uso común) una amplia variedad de conjuntos de bases atómicas gaussianas. Se puede acceder a este sitio aquí. El profesor Kirk Peterson de la Universidad Estatal de Washington está involucrado en el proyecto de desarrollo de conjuntos de bases PNNL, pero también alberga su propio sitio de base.

Funciones de polarización

Uno suele mejorar cualquier conjunto de bases de núcleo y valencia con un conjunto de las llamadas funciones de polarización. Son funciones de un momento angular superior al que aparece en el espacio orbital de valencia del átomo (por ejemplo,\(d\) -funciones para C, N y O y\(p\) -funciones para H), y tienen exponentes (\(z\)o\(a\)) que hacen que sus tamaños radiales sean similares a los tamaños de los orbitales de valencia ( es decir, los\(p\) orbitales de polarización del átomo de H son similares en tamaño al\(1s\) orbital más que al orbital de\(2s\) valencia del hidrógeno). Por lo tanto, no son orbitales que describan la valencia orbital del átomo con un valor l mayor; tales orbitales de valencia de mayor l serían radialmente más difusos.

Un propósito principal de las funciones de polarización es dar flexibilidad angular adicional al proceso LCAO en la formación de orbitales de unión entre pares de orbitales atómicos de valencia. Esto se ilustra en la Figura 6.1.2 donde se observa que los orbitales dp de polarización en C y O contribuyen a la formación del\(p\) orbital de enlace de un grupo carbonilo al permitir la polarización del\(p_\pi\) orbital del átomo de carbono hacia la derecha y del\(p_\pi\) orbital del átomo de oxígeno hacia la izquierda.

Figura 6.1.2 El oxígeno y el carbono forman un\(\pi\) enlace que utiliza las funciones de polarización en cada átomo

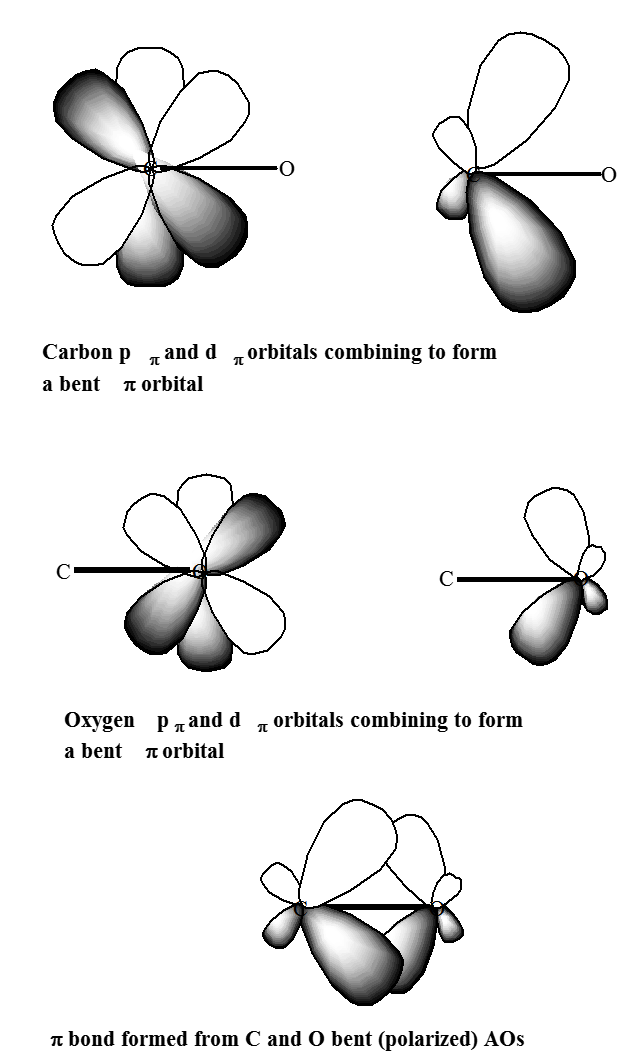
Las funciones de polarización son esenciales en compuestos de anillos tensos como el ciclopropano porque proporcionan la flexibilidad angular necesaria para dirigir la densidad de electrones hacia regiones entre átomos unidos, pero también son importantes en compuestos no deformados cuando se requiere alta precisión.

Funciones difusas

Al tratar con aniones o estados de Rydberg, uno debe aumentar aún más el conjunto de bases AO agregando los llamados orbitales de base difusa. Las funciones de valencia y polarización descritas anteriormente no proporcionan suficiente flexibilidad radial para describir adecuadamente ninguno de estos casos. La base de datos del sitio web PNNL citada anteriormente ofrece una buena fuente para obtener funciones difusas apropiadas para una variedad de átomos como lo hace el sitio del Prof. Kirk Peterson.

Una vez que se ha especificado una base orbital atómica para cada átomo de la molécula, se puede utilizar el procedimiento LCAO-MO para determinar los\(\chi_{\mu,i}\) coeficientes que describen los orbitales ocupados y virtuales (es decir, desocupados). Es importante tener en cuenta que los orbitales base no son en sí mismos los orbitales SCF de los átomos aislados; incluso los orbitales atómicos propiamente dichos son combinaciones (con valores atómicos para los\(\chi_{\mu,i}\) coeficientes) de las funciones base. El propio proceso LCAO-MO-SCF determina las magnitudes y signos de la\(\chi_{\nu,i}\). En particular, es que las alternancias en los signos de estos coeficientes permiten que se formen nodos radiales.