7.1: Colecciones de moléculas en o cerca del equilibrio

Como se introdujo en el Capítulo 5, el enfoque que se adopta al estudiar un sistema compuesto por un gran número de moléculas en o cerca del equilibrio térmico puede ser bastante diferente de cómo se estudian sistemas que contienen algunas moléculas aisladas. En principio, es posible concebir el cálculo de los niveles de energía cuántica y las funciones de onda de una colección de muchas moléculas (por ejemplo, diez\(Na^+\)\(Cl^-\) iones, diez iones y 550\(H_2O\) moléculas en un volumen elegido para simular una concentración de 1 molar\(NaCl_{(aq)}\)), pero hacerlo se convierte poco práctico una vez que el número de átomos en el sistema alcanza unos pocos miles o si las moléculas tienen interacciones intermoleculares significativas como lo hacen en los sistemas de fase condensada. Además, como se señala en el Capítulo 5, seguir la evolución temporal de un número tan grande de moléculas puede resultar confuso si uno se enfoca en el comportamiento a corto plazo de una sola molécula (por ejemplo, se ven cambios bruscos en su energía, impulso e impulso angular). Al examinar, en cambio, el comportamiento promedio a largo plazo de cada molécula o, alternativamente, las propiedades promedio de un número significativamente grande de moléculas, a menudo uno es más capaz de entender, interpretar y simular tales sistemas de medios condensados. Además, la mayoría de los experimentos no sondean tales propiedades dinámicas de corto tiempo de moléculas individuales; en su lugar, sus señales informan sobre el comportamiento de muchas moléculas que se encuentran dentro del rango de su dispositivo de detección (por ejemplo, haz láser, punta STM o electrodo). Es cuando se quiere describir el comportamiento de colecciones de moléculas bajo tales condiciones que entra en juego el poder de la mecánica estadística.

Distribución de Energía entre Niveles

Uno de los conceptos más importantes de la mecánica estadística consiste en cómo una determinada cantidad total de energía\(E\) puede ser compartida entre una colección de moléculas y dentro de los grados de libertad interna (rotacional, vibracional, electrónica) e intermolecular (traslacional) de estas moléculas cuando las moléculas tienen un medio para compartir o redistribuir esta energía (por ejemplo, por colisiones). El resultado primario de preguntar cuál es la distribución más probable de energía entre un gran número\(N\) de moléculas dentro de un contenedor de volumen\(V\) que se mantiene en equilibrio por tal distribución de energía a una temperatura especificada\(T\) es la ecuación más importante en estadística mecánica, la fórmula poblacional de Boltzmann:

\[P_j = \dfrac{\Omega_j \exp(- E_j /kT)}{Q}.\]

Esta ecuación expresa la probabilidad\(P_j\) de encontrar el sistema (que, en el caso introducido anteriormente, es toda la colección de moléculas que\(N\) interactúan) en su estado\(j^{th}\) cuántico, donde\(E_j\) está la energía de este estado cuántico,\(T\) es la temperatura en K,\(\Omega_j\) es la degeneración del\(j^{th}\) estado, y el denominador\(Q\) es la llamada función de partición:

\[Q = \sum_j \Omega_j \exp\bigg(- \dfrac{E_j}{kT}\bigg).\]

El equivalente mecánico clásico de la fórmula cuántica de población de Boltzmann anterior para un sistema con un total de\(M\) coordenadas (denotadas\(q\) colectivamente, serían las coordenadas internas e intermoleculares de las\(N\) moléculas en el sistema) y\(M\) momenta (denotadas \(p\)) es:

\[P(q,p) = \dfrac{ h^{-M}\exp \bigg(- \dfrac{H(q, p)}{kT}\bigg)}{Q},\]

donde\(H\) está el hamiltoniano clásico,\(h\) es la constante de Planck, y la función de partición clásica\(Q\) es

\[Q = h^{-M} \int \exp \bigg(- \dfrac{H(q, p)}{kT}\bigg) dq \;dp .\]

Esta expresión de densidad de probabilidad, que debe integrarse a la unidad, contiene el factor de\(h^{-M}\) porque, como vimos en el Capítulo 1 cuando aprendimos sobre la acción clásica, la integral de un producto de impulso coordinado tiene unidades de la constante de Planck.

Observe que la fórmula de Boltzmann no dice que solo se puedan poblar aquellos estados de una energía en particular; da probabilidades distintas de cero para poblar todos los estados desde el más bajo hasta el más alto. No obstante, sí dice que los estados de mayor energía\(E_j\) son desfavorecidos por el\(\exp (- E_j /kT)\) factor, pero, si los estados de mayor energía tienen mayores degeneraciones\(\Omega_j\) (lo que suelen hacer), la población general de dichos estados puede no ser baja. Es decir, existe una competencia entre la degeneración estatal\(\Omega_j\), que tiende a crecer a medida que crece la energía del estado, y\(\exp (-E_j /kT)\) que disminuye con el aumento de la energía. Si el número de partículas\(N\) es enorme, la degeneración\(-\Omega\) crece como un alto poder (denotemos este poder como\(K\)) de\(E\) porque la degeneración está relacionada con el número de formas en que la energía puede distribuirse entre las\(N\) moléculas. De hecho,\(K\) crece al menos tan rápido como\(N\). Como resultado del\(-\Omega\) crecimiento como\(E^K\), la función del producto\(P(E) = E^K \exp(-E/kT)\) tiene la forma mostrada en la Fig. 7.1 (para\(K=10\), con fines ilustrativos)

Figura 7.1 Factor de ponderación\(P(E)\) de probabilidad en función de\(E\) for\(K\) = 10.

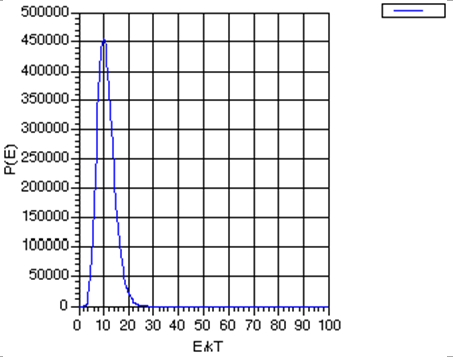
Al tomar la derivada de esta función\(P(E)\) con respecto a E, y encontrar la energía a la que esta derivada desaparece, se puede demostrar que esta función de probabilidad tiene un pico en\(E^* = K kT\), y que a este valor energético,

\[P(E^*) = (KkT)^K \exp(-K),\]

Para entonces preguntar a qué energía\(P(E)\) cae\(E'\) la función\(\exp(-1)\) de este valor máximo\(P(E^*)\):

\[P(E') = \exp(-1) P(E^*),\]

uno encuentra

\[E' = K kT \bigg(1+ \sqrt{\dfrac{2}{K}} \bigg).\]

Por lo que el ancho de la\(P(E)\) gráfica, medido como el cambio en la energía necesaria\(P(E)\) para hacer caer a\(\exp(-1)\) de su valor máximo dividido por el valor de la energía a la que\(P(E)\) asume este valor máximo, es

\[\dfrac{E'-E^*}{E^*} = \sqrt{\dfrac{2}{K}}.\]

Este ancho se hace cada vez más pequeño a medida que\(K\) aumenta.

La conclusión primaria es que a medida que crece el número\(N\) de moléculas en la muestra, lo que, como se discutió anteriormente, hace\(K\) que crezca, la función de probabilidad de energía se vuelve cada vez más pronunciada sobre la energía más probable\(E^*\). Esto, a su vez, sugiere que podemos modelar, aparte de fluctuaciones poco frecuentes que también podemos encontrar una manera de tener en cuenta, el comportamiento de sistemas con muchas moléculas enfocándonos en la situación más probable (es decir, aquellos que tienen la energía\(E^*\)) e ignorando o haciendo pequeñas correcciones para desviaciones de este caso.

Es por las razones que se acaban de mostrar que para los sistemas macroscópicos cercanos al equilibrio, en los que\(N\) (y por lo tanto\(K\)) es extremadamente grande (por ejemplo,\(N\) ~\(10^{10}\) a\(10^{24}\)), solo se necesita considerar la distribución más probable de la energía total entre\(N\) las moléculas. Esta es la situación en la que las ecuaciones de la mecánica estadística son tan útiles. Ciertamente, hay fluctuaciones (como lo demuestra el ancho finito de la gráfica anterior) en el contenido energético del sistema\(N\) -molécula sobre su valor más probable. Sin embargo, estas fluctuaciones se vuelven cada vez menos importantes a medida que el tamaño del sistema (es decir,\(N\)) se hace cada vez más grande.

Bases de la fórmula poblacional de Boltzmann

Para entender cómo surge esta estrecha distribución de energías de Boltzmann cuando el número de moléculas\(N\) en la muestra es grande, consideramos un sistema compuesto por recipientes\(M\) idénticos, cada uno con volumen V, y cada uno hecho de un material que permite una transferencia de calor eficiente a su entorno (ej., a través de colisiones de las moléculas dentro del volumen con las paredes del contenedor) pero material que no permite que ninguna de las\(N\) moléculas en cada contenedor escape. Estos recipientes están dispuestos en una celosía regular como se muestra en la Figura 7.2 de una manera que permite que sus paredes térmicamente conductoras entren en contacto. Por último, toda la colección de\(M\) dichos contenedores está rodeada por un material perfectamente aislante que asegura que la energía total (de todas las\(N \times M\) moléculas) no puede cambiar. Entonces, esta colección de contenedores\(M\) idénticos cada uno conteniendo\(N\) moléculas constituye un sistema cerrado (es decir, sin moléculas entrando o saliendo) y aislado (es decir, por lo que la energía total es constante).

Figura 7.2 Colección de celdas\(M\) idénticas que tienen paredes conductoras de energía que no permiten que las moléculas pasen entre células.

Suposición de probabilidad igual a priori

Uno de los supuestos fundamentales de la mecánica estadística es que, para un sistema aislado cerrado en equilibrio, todos los estados cuánticos del sistema que tengan energía igual a la energía\(E\) con la que se prepara el sistema tienen igual probabilidad de ser ocupados. Esto se llama la suposición de igual probabilidad a priori para tales estados cuánticos permitidos por energía. Los estados cuánticos relevantes para este caso no son los estados de moléculas individuales, ni son los estados\(N\) de las moléculas en uno de los contenedores de volumen\(V\). Son los estados cuánticos de todo el sistema compuesto por\(N\times M\) moléculas. Debido a que nuestro sistema consiste en contenedores\(M\) idénticos, cada uno con\(N\) moléculas en él, podemos describir los estados cuánticos de todo el sistema en términos de los estados cuánticos de cada uno de esos contenedores. Puede parecer una tontería estar discutiendo estados cuánticos del gran sistema que contiene\(N\times M\) moléculas, dado lo que dije antes sobre la futilidad al tratar de encontrar tales estados. No obstante, lo que estoy haciendo en esta etapa es llevar a cabo una derivación que se base en tales estados cuánticos pero cuya forma final y ecuaciones finales de trabajo no requerirán realmente que uno conozca o incluso pueda tener estos estados en la mano.

Pretendamos que conocemos los estados cuánticos que pertenecen a\(N\) las moléculas en un contenedor de volumen\(V\) como se muestra en la Figura 7.2, y etiquetemos estos estados mediante un índice\(J\). Es decir,\(J=1\) etiqueta el estado de menor energía de\(N\) las moléculas en el contenedor de volumen\(V\),\(J=2\) etiqueta el segundo estado de ese tipo, y así sucesivamente. Como dije anteriormente, entiendo que puede parecer desalentador pensar en cómo se encuentran realmente estos autoestados de\(N\) moléculas. No obstante, solo estamos derivando un marco general que da las probabilidades de estar en cada uno de esos estados. Al hacerlo, se nos permite fingir que conocemos estos estados. En cualquier aplicación real, tendremos, por supuesto, que usar expresiones aproximadas para tales energías.

Suponiendo que las paredes que dividen los\(M\) contenedores no juegan ningún papel excepto para permitir la transferencia de energía colisional (es decir, térmica) entre los contenedores, se puede realizar un etiquetado energético para los estados de toda la colección de\(M\) contenedores dando el número de contenedores que existen en cada de un solo contenedor J-State. Esto es posible porque, bajo el supuesto sobre el papel de los muros que acabamos de enunciar, la energía de cada estado\(M\) -contenedor es una suma de las energías de los estados de\(M\) un solo contenedor que comprenden ese estado\(M\) -contenedor. Por ejemplo, si\(M= 9\), la etiqueta 1, 1, 2, 2, 1, 3, 4, 1, 2 especifica la energía de este estado de 9 contenedores en términos de las energías {\(\varepsilon_j\)} de los estados de los 9 contenedores:\(E = 4\varepsilon_1 + 3\varepsilon_2 + \varepsilon_3 + \varepsilon_4\). Observe que este estado de 9 contenedores tiene la misma energía que varios otros estados de 9 contenedores; por ejemplo, 1, 2, 2, 1, 3, 4, 1, 2 y 4, 1, 3, 1, 2, 2, 1, 1, 2, 1, 2 tienen la misma energía aunque son diferentes estados individuales. Lo que difiere entre estos estados distintos es qué caja ocupa qué estado cuántico de caja única.

El ejemplo anterior ilustra que un nivel de energía del sistema\(M\) -container puede tener un alto grado de degeneración debido a que su energía total se puede lograr haciendo que los diversos estados de un solo contenedor aparezcan en diversos órdenes. Es decir, qué contenedor se encuentra en qué estado se puede permutar sin alterar la energía total\(E\). La fórmula de cuántas formas los estados del\(M\) contenedor pueden permutarse de tal manera que:

1. hay\(n_J\) contenedores que aparecen en estado de contenedor único\(J\), con
2. un total de\(M\) contenedores, es

\[\Omega(n) = \dfrac{M!}{\prod_Jn_J!}.\]

Aquí\(n = \{n_1, n_2, n_3, \cdots n_J, \cdots \}\) denotan el número de contenedores existentes en estados de contenedor único 1, 2, 3,...\(J\),... Esta fórmula combinatoria refleja la degeneración permutacional que surge de colocar\(n_1\) los contenedores en el estado 1,\(n_2\) los contenedores en el estado 2, etc.

Si imaginamos un número extremadamente grande de contenedores y vemos así\(M\) como los {\(n_J\)} como números grandes (n.b., pronto veremos que este es el caso al menos para la distribución más probable en la que eventualmente nos centraremos), podemos preguntar- qué opciones de las variables\(\{n_1, n_2, n_3, \cdots n_J, \cdots \}\) ¿esta función de degeneración\(\Omega(n)\) es máxima? Además, podemos examinar\(\Omega(n)\) en su máximo y comparar su valor en valores de los {\(n\)} parámetros cambiados solo ligeramente de los valores que maximizaron\(\Omega(n)\). Como veremos,\(-\Omega\) está muy fuertemente pico en su máximo y disminuye extremadamente rápidamente para valores de {\(n\)} que difieren sólo ligeramente de los valores óptimos. Es esta propiedad la que da origen a la distribución muy estrecha de la energía que se discutió anteriormente en este Capítulo. Entonces, echemos un vistazo más de cerca a cómo surge esta fórmula de distribución de energía.

Queremos saber qué valores de las variables\(\{n_1, n_2, n_3, \cdots n_J, \cdots \}\) hacen\(-\Omega = M!/{\Pi_Jn_J!}\) un máximo. Sin embargo, todas las\(\{n_1, n_2, n_3, \cdots n_J, \cdots \}\) variables no son independientes; deben sumar\(M\), el número total de contenedores, por lo que tenemos una restricción

\[\sum_J n_J = M\]

que las variables deben obedecer. Las variables {\(n_j\)} también están restringidas para dar la energía total\(E\) del sistema\(M\) -container cuando se suman como

\[\sum_J n_J\varepsilon_J = E.\]

Tenemos dos problemas: i. cómo maximizar\(-\Omega\) y ii. cómo imponer estas restricciones. Porque\(-\Omega\) toma valores mayores que la unidad para cualquier elección del {\(n_j\)},\(-\Omega\) experimentará su máximo donde\(\ln\Omega\) tenga su máximo, así podremos maximizar\(\ln \Omega\) si hacerlo ayuda. Debido a que se supone que las\(n_J\) variables toman números grandes (cuando\(M\) es grande), podemos usar la aproximación de Sterling para el logaritmo natural del factorial de un número grande:

\[\ln X! \approx X \ln X – X\]

para aproximarse de\(\ln \Omega\) la siguiente manera:

\[\ln \Omega \approx \ln M! - \sum_J (n_J \ln n_J – n_J).\]

Esta expresión resultará útil porque podemos tomar su derivada con respecto a las\(n_J\) variables, que debemos hacer para buscar el máximo de\(\ln \Omega\).

Para imponer las restricciones\(\sum_J n_J = M\) y\(\sum_J n_J \varepsilon_J = E\) utilizamos la técnica de multiplicadores Lagrange. Es decir, buscamos encontrar valores de {\(n_J\)} que maximicen la siguiente función:

\[F = \ln M! - \sum_J (n_J \ln n_J – n_J) - \alpha(\sum_Jn_J – M) - \beta(\sum_J n_J \varepsilon_J –E).\]

Observe que esta función\(F\) es exactamente igual a la\(\ln\Omega\) función que deseamos maximizar siempre que las variables {\(n_J\)} obedezcan a las dos restricciones. Entonces, los máximos de\(F\) y de\(\ln\Omega\) son idénticos si los {\(n_J\)} tienen valores que obedecen a las restricciones. Los dos multiplicadores Lagrange\(\alpha\) y\(\beta\) se introducen para permitir que los valores de {\(n_J\)} que maximizan\(F\) obedezcan en última instancia las dos restricciones. Es decir, primero encontramos valores de las {\(n_J\)} variables que hacen\(F\) máximo; estos valores dependerán\(\alpha\)\(\beta\) y no necesariamente obedecerán las restricciones. No obstante, entonces elegiremos\(\alpha\) y\(\beta\) aseguraremos que se obedezcan las dos limitaciones. Así es como funciona el método multiplicador Lagrange.

Método del multiplicador de Lagrange

Tomando la derivada de\(F\) con respecto a cada\(n_K\) variable independiente y estableciendo esta derivada igual a cero da:

\[- \ln n_K - \alpha - \beta \varepsilon_K = 0.\]

Esta ecuación se puede resolver para dar\(n_K = \exp(- \alpha) \exp(- \beta \varepsilon_K)\). Sustituir este resultado en la primera ecuación de restricción da\(M = \exp(- \alpha) \sum_J \exp(- \beta \varepsilon_J)\), lo que nos permite resolver para

\(\exp(- \alpha)\)en términos de\(M\). Hacerlo, y sustituir el resultado en la expresión para\(n_K\) da:

\[n_K = M\dfrac{\exp(- \beta \varepsilon_K)}{Q}\]

donde

\[Q = \sum_J \exp(- \beta \varepsilon_J).\]

Observe que los\(n_K\) son, como suponíamos antes, números grandes si\(M\) es grande porque\(n_K\) es proporcional a\(M\). Observe también que ahora vemos la aparición de la función de partición\(Q\) y de dependencia exponencial de la energía del estado que da a la población Boltzmann de ese estado.

Es posible relacionar el multiplicador\(\beta\) Lagrange con la energía total\(E\) de los\(M\) contenedores sumando el número de contenedores en el estado cuántico Kth\(n_K\) multiplicado por la energía de ese estado cuántico\(\varepsilon_K\)

\[ \begin{algin*} E &= \sum_K n_K \varepsilon_K \\[4pt] &= M\sum_K \dfrac{\varepsilon_K\exp(- \beta \varepsilon_K)}{Q} \\[4pt] &= - M\left(\frac{∂\ln Q}{∂\beta} \right)_{N,V}. \end{align*}\]

Esto demuestra que la energía promedio de un contenedor, calculada como la energía total\(E\) dividida por el número\(M\) de dichos contenedores, puede calcularse como una derivada del logaritmo de la función de partición\(Q\). Como mostramos en la siguiente Sección de este Capítulo, todas las propiedades termodinámicas de las\(N\) moléculas en el contenedor de volumen se\(V\) pueden obtener como derivadas del logaritmo natural de esta\(Q\) función. Es por ello que la función de partición juega un papel tan central en la mecánica estadística.

Para examinar el rango de energías sobre el cual cada uno de los sistemas de\(M\) un solo contenedor varía con probabilidad apreciable, consideremos no solo la degeneración\(\Omega(n^*)\) de ese conjunto de variables\(\{n^*\} = \{n^*_1, n^*_2, \cdots \}\) que hace\(-\Omega\) máximo, sino también la degeneración\(\Omega(n)\) para los valores de\(\{n_1, n_2, \cdots\}\) difiriendo por pequeñas cantidades {\(\delta n_1, \delta n_2, \cdots\)} de los valores óptimos {\(n^*\)}. Ampliando\(\ln \Omega\) como una serie Taylor en los parámetros\(\{n_1, n_2, \cdots\}\) y evaluando la expansión en el vecindario de los valores {\(n^*\)}, encontramos:

\[\ln \Omega = \ln \Omega({n^*_1, n^*_2, …}) + \sum_J \left(\frac{∂\ln\Omega}{∂n_J}\right) \delta n_J + \frac{1}{2} \sum_{J,K} \left(\frac{∂^2\ln\Omega}{∂n_J∂n_K}\right) \delta n_J \delta n_K + …\]

Sabemos que todos los primeros términos derivados (\(\dfrac{∂\ln\Omega}{∂n_J}\)) desaparecen porque se\(\ln\Omega\) ha hecho máximo en {\(n^*\)}. Para evaluar los términos de la segunda derivada, primero observamos que la primera derivada de\(\ln\Omega\) es

\[\left(\frac{∂\ln\Omega}{∂n_J}\right) = \frac{∂(\ln M! - \sum_J (n_J \ln n_J – n_J))}{∂n_J} = -\ln(n_J).\]

Entonces, las segundas derivadas necesarias para completar la serie Taylor a través de segundo orden son:

\[\left(\frac{∂^2\ln\Omega}{∂n_J∂nK}\right) = - \frac{\delta_{J,K}}{n_j}.\]

Usando este resultado, podemos expandirnos\(\Omega(n)\) en el barrio de {\(n^*\)} en poderes de la\(\delta n_J = n_J-n_J^*\) siguiente manera:

\[\ln \Omega(n) = \ln \Omega(n^*) – \frac{1}{2} \frac{\sum_J (\delta n_J)^2}{n_J^*},\]

o, equivalentemente,

\[\Omega(n) = \Omega(n^*) \frac{\exp[-\frac{1}{2}\sum_J (\delta n_J)^2]}{n_J^*}\]

Este resultado muestra claramente que la degeneración, y por lo tanto, por la hipótesis de probabilidad igual a priori, la probabilidad de que el sistema\(M\) -contenedor ocupe un estado que tiene {\(n_1, n_2, \cdots\)} cae exponencialmente a medida que las variables\(n_J\) se alejan de sus valores más probables {\(n^*\)}.

Límite termodinámico

Como señalamos anteriormente, los\(n_J^*\) son proporcionales a\(M\) (es decir,\(n_J^* = \dfrac{M\exp(-\beta\varepsilon_J)}{Q} = f_J M\)), por lo que al considerar desviaciones\(\delta n_J\) alejadas de lo óptimo\(n_J^*\), debemos considerar desviaciones que también son proporcionales a\(M\):\(\delta n_J = M \delta f_J\). De esta manera, estamos tratando desviaciones del porcentaje especificado o cantidad fraccional que denotamos\(f_J\). Así, la relación\(\dfrac{(\delta n_J)^2}{n_J^*}\) que aparece en el exponencial anterior tiene una dependencia M que\(\Omega(n)\) permite escribirse como:

\[\Omega(n) = \Omega(n^*) \exp\left[-\dfrac{M}{2}\sum_J \dfrac{(\delta f_J)^2}{f_J^*}\right],\]

donde\(f_J^*\) y\(\delta f_J\) son la fracción y desviación fraccional de los contenedores en estado\(J\):\(f_J^* = \dfrac{n_J^*}{M}\) y\(\delta f_J = \dfrac{\delta n_J}{M}\). El propósito de escribir\(\Omega(n)\) de esta manera es mostrar explícitamente que, en el llamado límite termodinámico, cuando se\(M\) acerca al infinito, solo se necesita considerar la distribución más probable de la energía {\(n^*\)} porque solo {\(\delta f_J=0\)} es importante a medida que se\(M\) acerca al infinito.

Fluctuaciones

Consideremos un poco más este tema de distribución muy estrecha examinando las fluctuaciones en la energía de un solo contenedor alrededor de su energía promedio\(E_{\rm ave} = \dfrac{E}{M}\). Ya sabemos que el número de contenedores en un estado dado se\(K\) puede escribir como\(n_K = \dfrac{M\exp(- \beta \varepsilon_K)}{Q}\). Alternativamente, podemos decir que la probabilidad de que un contenedor ocupe el estado\(J\) es:

\[p_J = \dfrac{\exp(- \beta \varepsilon_K)}{Q}.\]

Usando esta probabilidad, podemos calcular la energía promedio\(E_{\rm ave}\) como:

\[E_{\rm ave} = \sum_J p_J \varepsilon_J = \dfrac{\sum_J \varepsilon_J \exp(- \beta \varepsilon_K)}{Q} = - \left(\dfrac{∂\ln Q}{∂\beta} \right)_{N,V}.\]

Para calcular la fluctuación en la energía, primero observamos que la fluctuación se define como el promedio del cuadrado de la desviación en energía del promedio:

\[(E-E_{\rm ave})^2_{\rm ave} = \sum_J (\varepsilon_J –E_{\rm ave})^2 p_J = \sum_J p_J (\varepsilon_J^2 - 2\varepsilon_J E_{\rm ave} +E_{\rm ave}^2) = \sum_J p_J(\varepsilon_J^2 – E_{\rm ave}^2).\]

La siguiente identidad es ahora útil para reexpresar aún más las fluctuaciones:

\[\left(\dfrac{∂^2\ln Q}{∂\beta^2}\right)_{N,V} = \dfrac{ ∂\left( -\sum_J\dfrac{\varepsilon_J \exp(-\beta\varepsilon_J)}{Q} \right) }{∂\beta}\]

\[= \sum_J \dfrac{\varepsilon_J^2\exp(-\beta\varepsilon_J)}{Q} - \left(\sum_J \dfrac{\varepsilon_J\exp(-\beta\varepsilon_J)}{Q}\right) \left(\sum_L \dfrac{\varepsilon_L\exp(-\beta\varepsilon_​L)}{Q}\right)\]

Reconocer el primer factor inmediatamente anterior como\(\sum_J \varepsilon_J^2 p_J\), y el segundo factor como\(- E_{\rm ave}^2\), y señalar que\(\sum_J p_J = 1\), permite que la fórmula de fluctuación se reescriba como:

\[(E-E_{\rm ave})^2_{\rm ave} = \left(\dfrac{∂^2\ln Q}{∂\beta^2}\right )_{N,V} = - \left(\dfrac{∂E_{\rm ave}}{∂\beta}\right)_{N,V}.\]

Debido a que se\(\beta\) puede mostrar que el parámetro está relacionado con la temperatura Kelvin\(T\) como\(\beta =\dfrac{1}{kT}\), la expresión anterior se puede reescribir como:

\[(E-E_{\rm ave})^2_{\rm ave} = - \left(\dfrac{∂ E_{\rm ave}}{∂\beta}\right)_{N,V} = kT^2 \left(\dfrac{∂E_{\rm ave}}{∂T}\right)_{N,V}.\]

Reconocer la fórmula para la capacidad calorífica de volumen constante

\[C_V = \left(\dfrac{∂E_{\rm ave}}{∂T}\right)_{N,V}\]

permite que la fluctuación fraccionaria en la energía alrededor de la energía media\(E_{\rm ave} = \dfrac{E}{M}\) se exprese como:

\[\dfrac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2} = \dfrac{kT^2 C_V}{E_{\rm ave}^2}.\]

¿Qué nos dice esta fórmula de fluctuación fraccional? En su lado izquierdo da una medida de la dispersión fraccionaria de las energías sobre la cual cada uno de los contenedores oscila alrededor de su energía media\(E_{\rm ave}\). En el lado derecho, contiene una relación de dos cantidades que son propiedades extensas, la capacidad calorífica y la energía media. Es decir, ambos\(C_V\) y\(E_{\rm ave}\) serán proporcionales al número\(N\) de moléculas en el contenedor siempre y cuando\(N\) sea razonablemente grande. Sin embargo, debido a que el lado derecho implica\(C_V/E_{\rm ave}^2\), es proporcional\(N-1\) y por lo tanto será muy pequeño para grandes\(N\) siempre y cuando\(C_V\) no se haga grande. Como resultado, excepto cerca de los llamados puntos críticos donde la capacidad calorífica de hecho se vuelve extremadamente grande, la fluctuación fraccionaria en la energía de un contenedor dado de\(N\) moléculas será muy pequeña (es decir, proporcional a\(N-1\)). Este hallazgo está relacionado con la estrecha distribución en energías que discutimos anteriormente en esta sección.

Veamos la expresión

\[\dfrac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2} = \frac{kT^2 C_V}{E_{\rm ave}^2}\]

con un poco más de detalle para un sistema que es pequeño pero que aún contiene bastantes partículas, un cúmulo de átomos de\(N\) Ar a temperatura\(T\). Si asumimos que cada uno de los átomos de Ar en el cúmulo tiene\(\dfrac{3}{2} kT\) de energía cinética y que la energía potencial que mantiene unido al cúmulo es pequeña y constante (por lo que se cancela en\(E-E_{\rm ave}\)),\(E_{\rm ave}\)\(C_V\) será\(\dfrac{3}{2}NkT\) y será\(\dfrac{3}{2} Nk\). Entonces,

\[\frac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2} = \frac{kT^2 C_V}{E_{\rm ave}^2} = kT^2 \dfrac{\dfrac{3}{2}Nk}{\bigg(\dfrac{3}{2} NkT\bigg)^2} = \frac{2}{3 N}.\]

En una nano-gotita de diámetro 100 Å, con cada átomo de Ar ocupando un volumen de ca.\(4/3 \pi (3.8Å)^3 = 232 Å^3\), habrá ca.

\[N = \frac{4}{3} \pi \dfrac{100^3}{\dfrac{4}{3} \pi 3.83} = 1.8 \times10^4\]

Átomos de Ar. Entonces, el diferencial fraccional promedio en la energía

\[\sqrt{\frac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2}} = \sqrt{\frac{2}{3 N}}=0.006.\]

Es decir, incluso para una nanogotita muy pequeña, la fluctuación en la energía del sistema es solo una fracción de un porcentaje (asumiendo que no\(C_V\) es grande tan cerca de un punto crítico). Este ejemplo muestra por qué a menudo es posible utilizar conceptos y ecuaciones termodinámicas incluso para sistemas muy pequeños, aunque dándose cuenta de que las fluctuaciones alejadas del estado más probable son más importantes que en sistemas mucho más grandes.

Funciones de partición y propiedades termodinámicas

Examinemos ahora cómo esta idea de que la distribución de energía más probable es dominante da lugar a ecuaciones que ofrecen expresiones de nivel molecular para otras propiedades termodinámicas. La primera ecuación es la fórmula poblacional fundamental de Boltzmann que ya examinamos:

\[P_j = \dfrac{\exp(- E_j /kT)}{Q},\]

que expresa la probabilidad de encontrar el sistema\(N\) -molécula en su estado\(J^{\rm th}\) cuántico teniendo energía\(E_j\). A veces, esta expresión se escribe como

\[P_j = \dfrac{\Omega_j \exp(- E_j /kT)}{Q}\]

donde ahora el índice\(j\) se utiliza para etiquetar un nivel de energía del sistema que tiene energía\(E_j\) y degeneración. Es importante que el alumno esté acostumbrado a cualquiera de las dos anotaciones; un nivel es solo una colección de aquellos estados que tienen idéntica energía.

Funciones de partición del sistema

Usando este resultado, es posible calcular la energía promedio\(E_{\rm ave}\), a veces escrita como\(\langle E \rangle\), del sistema

\[\langle E \rangle = \sum_j P_j E_j ,\]

y, como vimos anteriormente en este Capítulo, para demostrar que esta cantidad puede ser refundido como

\[\langle E \rangle = kT^2 \left(\frac{∂\ln Q}{∂T}\right)_{N,V} .\]

Para revisar cómo se lleva a cabo esta prueba, sustituimos las expresiones para\(P_j\) y para\(Q\) en la expresión para\(\langle E \rangle\) (usaré la notación etiquetando niveles de energía en lugar de estados energéticos para permitir que el estudiante se acostumbre a esto)

\[\langle E \rangle = \frac{\sum_j E_j \Omega_j \exp(-E_j/kT)}{\sum_I \Omega_I\exp(-E­_l/kT)}.\]

Al señalar que\(\dfrac{∂ (\exp(-E­_j/kT))}{∂T} = \dfrac{1}{kT^2} E_j \exp(-E_j/kT)\), entonces podemos reescribir\(\langle E \rangle\) como

\[\langle E \rangle = kT^2 \frac{\sum_j \Omega_j \dfrac{∂ (\exp(-E­_j/kT))}{∂T} }{\sum_I \Omega_I\exp(-E­_l/kT)}.\]

Y luego recordando eso\(\dfrac{∂X/∂T}{X} = \dfrac{∂\ln X}{∂T}\), finalmente obtenemos

\[\langle E \rangle = kT^2 \left(\frac{∂\ln Q}{∂T}\right)_{N,V}.\]

Todas las demás propiedades de equilibrio también se pueden expresar en términos de la función de partición\(Q\). Por ejemplo, si la presión promedio\(\langle p \rangle\) se define como la presión de cada estado cuántico (definida como cómo cambia la energía de ese estado si cambiamos el volumen del contenedor en una pequeña cantidad)

\[p_j = \bigg(\frac{∂E_j}{∂V}\bigg)_N\]

multiplicado por la probabilidad\(P_j\) de acceder a ese estado cuántico, sumado sobre todos esos estados, se puede mostrar, dándose cuenta de que solo\(E_j\) (no\(T\) o\(W\)) dependen del volumen\(V\), que

\[\langle p \rangle = \sum_j \bigg(\frac{∂E_j}{∂V}\bigg)\dfrac{N \Omega_j \exp(- E_j /kT)}{Q}\]

\[= kT\left(\frac{∂\ln Q}{∂V}\right)_{N,T} .\]

Si te preguntas por qué las energías\(E_J\) deben depender del volumen\(V\), piensa en el caso de las moléculas en\(N\) fase gaseosa que ocupan el contenedor del volumen V. Ya sabes que las energías traslacionales de cada una de estas\(N\) moléculas dependen del volumen a través de la fórmula partícula-en-a-caja

\[E_{n_x,n_y,n_z}=\dfrac{\hbar^2}{8mL^2}(n_x^2+n_y^2+n_z^2).\]

El cambio se\(V\) puede lograr cambiando la longitud de la caja\(L\). Esto deja claro por qué las energías sí dependen del volumen\(V\). Por supuesto, hay fuentes adicionales de la dependencia V de los niveles de energía. Por ejemplo, a medida que uno se encoge\(V\), las moléculas se vuelven más abarrotadas, por lo que sus energías intermoleculares también cambian.

Sin belaboring más el punto, es posible expresar todas las cantidades termodinámicas habituales en términos de la función de partición\(Q\). La energía promedio y la presión promedio se dan arriba, al igual que la capacidad calorífica. La entropía promedio se da como

\[\langle S\rangle = k \ln Q + kT \left(\frac{∂\ln Q}{∂N}\right)_{V,T}\]

la energía libre de Helmholtz A es

\[A = -kT \ln Q\]

y el potencial químico\(\mu\) se expresa de la siguiente manera:

\[\mu = -kT \left(\frac{∂\ln Q}{∂N}\right)_{T,V}.\]

Como vimos anteriormente, también es posible expresar fluctuaciones en las propiedades termodinámicas en términos de derivados de funciones de partición y, así, como derivados de otras propiedades. Por ejemplo, la fluctuación en la energía\(\langle (E-\langle E\rangle )^2\rangle\) se mostró arriba para ser dada por

\[\langle (E-\langle E\rangle )^2\rangle = kT^2 C_V.\]

El texto Mecánica Estadística, D. A. McQuarrie, Harper y Row, Nueva York (1977) tiene un excelente tratamiento de estos temas y muestra cómo se derivan todas estas expresiones.

Entonces, si uno fuera capaz de evaluar la función de partición\(Q\) para\(N\) moléculas en un volumen\(V\) a una temperatura T, ya sea sumando la degeneración de nivel cuántico y\(\exp(-E_j/kT)\) los factores

\[Q = \sum_j \Omega_j \exp(- E_j /kT),\]

o realizando la integral fase-espacio sobre todas\(M\) las coordenadas y momentos del sistema

\[Q = h^{-M} \int \exp \bigg(- \dfrac{H(q, p)}{kT}\bigg) dq \; dp ,\]

entonces se podrían usar las fórmulas anteriores para evaluar cualquier propiedad termodinámica y sus fluctuaciones como derivados de\(\ln Q\).

Los promedios discutidos anteriormente, derivados utilizando las probabilidades\(p_J = \dfrac{\Omega_J \exp(- E_J /kT)}{Q}\) asociadas a la distribución más probable, se denominan promedios conjuntos con el conjunto de estados asociados a los valores especificados de\(N\),\(V\), y\(T\) que constituyen lo que se llama un conjunto canónico. Promedios derivados usando las probabilidades\(\Pi_J\) = constante para todos los estados asociados con valores especificados de\(N\)\(V\), y\(E\) se denominan promedios de conjunto para un conjunto microcanónico. Hay otro tipo de conjunto que se usa a menudo en la mecánica estadística; se llama el gran conjunto canónico y se relaciona con sistemas con volumen\(V\)\(T\), temperatura y potencial químico especificados\(\mu\) (en lugar de número de partículas\(N\)). Para obtener la función de partición (de la que se obtienen todas las propiedades termodinámicas) en este caso, se considera maximizar la misma función

\[\Omega(n) = \dfrac{M!}{\prod_Jn_J!}\]

introducido anteriormente, pero ahora considerando cada cuántico (etiquetado J) como que tiene una energía\(E_J(N,V)\) que depende del volumen y de cómo pueden las partículas ocupar este volumen. Las variables\(n_J(N)\) ahora se utilizan para especificar cuántos de los contenedores introducidos anteriormente contienen\(N\) partículas y están en estado\(J^{\rm th}\) cuántico. Estas variables tienen que obedecer las mismas dos restricciones que para el conjunto canónico

\[\sum_J,N n_J(N) = M\]

\[\sum_J,N n_J(N) \varepsilon_J(N,V) =E,\]

pero también están obligados a obedecer

\[\sum_{J,N} N n_J(N) = N_{\rm total}\]

lo que significa que la suma suma suma el número total de partículas en el contenedor grande del sistema aislado que se dividió en M contenedor más pequeño. En este caso, se supone que las paredes que separan cada recipiente pequeño permiten la transferencia de energía (como en el conjunto canónico) y que las moléculas se muevan de un recipiente a otro (a diferencia del conjunto canónico). El uso de multiplicadores Lagrange como antes para maximizar\(\ln\Omega(n)\) sujeto a las tres restricciones anteriores implica maximizar

\[F = \ln M!-\sum_{J,N} (n_{J,N} \ln n_{J,N} – n_{J,N}) - \alpha(\sum_{J,N} n_{J,N} – M) -\beta(\sum_{J,N} n_{J,N} \varepsilon_J –E) –\gamma(\sum_{J,N} N n_{J,N}(N) - N_{\rm total})\]

y da

\[- \ln n_{K,N} - \alpha - \beta \varepsilon_K -\gamma N = 0\]

o

\[n_{K,N} = \exp[- \alpha - \beta \varepsilon_K -\gamma N].\]

La imposición de la primera restricción da

\[M = \sum_{K,N}\exp[- \alpha - \beta \varepsilon_K -\gamma N],]\]

o

\[\exp(-\alpha)=\frac{M}{\sum_{K,N}\exp(-\beta\varepsilon_K(N)-\gamma N)}=\frac{M}{Q(\gamma,V,T)}\]

donde la función de partición\(Q\) se define por la suma en el denominador. Entonces, ahora la probabilidad de que el sistema tenga\(N\) partículas y esté en el estado\(K^{\rm th}\) cuántico es

\[P_K(N)=\frac{\exp(-\beta\varepsilon_K(N)-\gamma N)}{Q}.\]

Muy como se demostró anteriormente para el conjunto canónico, entonces se pueden expresar propiedades termodinámicas (e.g.,\(E\),\(C_V\), etc.) en términos de derivados de\(\ln Q\). El texto Mecánica Estadística, D. A. McQuarrie, Harper y Row, Nueva York (1977) pasa por estas derivaciones con buen detalle, así que no voy a repetirlas aquí porque mostramos cómo hacerlo al tratar al conjunto canónico. Para resumirlos brevemente, se utiliza nuevamente\(\beta = \dfrac{1}{kT}\), encuentra que g está relacionado con el potencial químico\(\mu\) como

\[\gamma = - \mu \beta\]

y obtiene

\[p=\sum_{N,K} P_K(N)\left(\frac{-\partial \varepsilon_K(N,V)}{\partial V}\right)_N=kT \left(\frac{-\partial Q}{\partial V}\right)_{\mu,T}\]

\[N_{\rm ave}=\sum_{N,K} N P_K(N)=kT \left(\frac{-\partial Q}{\partial \mu}\right)_{V,T}\]

\[S=kT\left(\frac{-\partial Q}{\partial T}\right)_{\mu,V}=k\ln Q\]

\[E=\sum_{N,K} \varepsilon_K(N)P_K(N)=kT^2 \left(\frac{-\partial Q}{\partial T}\right)_{\mu,V}\]

\[Q=\sum_{N,K} \exp(-\beta\varepsilon_K(N)+\mu\beta N).\]

Las fórmulas se parecen mucho a las del conjunto canónico, excepto por el resultado que expresa el número promedio de moléculas en el contenedor Nave en términos de la derivada de la función de partición con respecto al potencial químico\(\mu\).

Además del postulado de probabilidad igual a priori establecido anteriormente (es decir, que, en el límite termodinámico (es decir, grande\(N\)), cada estado cuántico de un sistema aislado en equilibrio que tiene fijo\(N\),\(V\), y\(E\) es igualmente probable), la mecánica estadística hace otro suposición. Se supone que, en el límite termodinámico, el promedio del conjunto (por ejemplo, usando probabilidades iguales\(\Pi_J\) para todos los estados de un sistema aislado que\(N\) haya especificado\(V\),\(E\) y/o usando\(P_j = \dfrac{\exp(- E_j /kT)}{Q}\) para estados de un sistema que haya especificado\(N\)\(V\), y\(T\) o usar\(P_K(N)=\dfrac{\exp(-\beta\varepsilon_K(N,V)+\mu\beta N)}{Q}\) para el gran caso canónico) de cualquier cantidad es igual al promedio a largo plazo de esta cantidad (es decir, el valor que se obtendría al monitorear la evolución dinámica de esta cantidad durante un tiempo muy largo). Este segundo postulado implica que la dinámica de un sistema aislado pasa cantidades iguales de tiempo en cada estado cuántico que tiene lo especificado\(N\),\(V\), y\(E\); esto se conoce como la hipótesis ergódica.

Consideremos un poco más cuál es el significado físico o el contenido de información de las funciones de partición. Las funciones de partición de conjunto canónico representan el número promedio térmico de estados cuánticos que son accesibles para el sistema a valores especificados de\(N\),\(V\), y\(T\). Esto se puede ver mejor al señalar nuevamente que, en la expresión cuántica,

\[Q = \sum_j \Omega_j \exp\bigg(- \dfrac{E_j}{kT}\bigg)\]

la función de partición es igual a una suma del número de estados cuánticos en el jésimo nivel de energía multiplicado por el factor poblacional de Boltzmann\(\exp(-E_j/kT)\) de ese nivel. Entonces,\(Q\) es adimensional y es una medida de cuántos estados puede acceder el sistema a temperatura\(T\). Otra forma de pensar\(Q\) se sugiere reescribiendo la definición de energía libre de Helmholtz dada anteriormente como\(Q = \exp(-A/kT)\). Esta identidad demuestra que\(Q\) puede ser vista como la población Boltzmann, no de una energía dada\(E\), sino de una determinada cantidad de energía libre\(A\).

Para el conjunto microcanónico, la probabilidad de ocupar cada estado que tenga los valores especificados de\(N\),\(V\), y\(E\) es igual

\[P_J = \dfrac{1}{\Omega(N,V, E)}\]

donde\(\Omega(N,V, E)\) está el número total de dichos estados. En el caso del conjunto microcanónico,\(\Omega(N,V, E)\) juega el papel que\(Q\) juega en el caso del conjunto canónico; da el número de estados cuánticos accesibles al sistema.

Funciones de partición de moléculas individuales

Tenga en cuenta que los niveles de energía\(E_j\) y las degeneraciones\(\Omega_j\) y\(\Omega(N,V, E)\) discutidos hasta ahora son los del sistema\(N\) de moléculas completas. En el caso especial para el cual se pueden descuidar las interacciones entre las moléculas (es decir, en el límite ideal-gas diluido) al menos en cuanto a expresar las energías del estado, cada una de las energías\(E_j\) puede escribirse como una suma de las energías de cada molécula individual:\(E_j = \sum_{k=1}^N \varepsilon_j(k)\). En tal caso, la función de partición anterior se\(Q\) reduce a un producto de funciones de partición de molécula individual:

\[Q = \frac{q_N}{N!} \]

donde el N! surge como un factor de degeneración que tiene que ver con la indistinguibilidad permutacional de las\(N\) moléculas (e.g., no se debe contar tanto\(\varepsilon_j(3) + \varepsilon_k(7)\) con la molécula 3 en estado\(j\) como con la molécula 7 en estado\(k\) y\(\varepsilon_j(7) + \varepsilon_k(3)\) con la molécula 7 en estado\(j\) y la molécula 3 en estado\(k\); son el mismo estado), y\(q\) es la función de partición de una molécula individual

\[q = \sum_l \omega_l \exp\bigg(-\dfrac{\varepsilon_l}{kT}\bigg).\]

Aquí,\(\varepsilon_l\) está la energía del nivel lésimo de la molécula y\(\omega_l\) es su degeneración.

Las funciones de partición molecular\(q\), a su vez, pueden escribirse como productos de funciones de partición traslacional, rotacional, vibracional y electrónica si las energías moleculares\(\varepsilon_l\) pueden aproximarse como sumas de tales energías. Por supuesto, estas aproximaciones son las más apropiadas para moléculas en fase gaseosa cuyos estados de vibración y rotación se están describiendo en el nivel más bajo.

Las siguientes ecuaciones dan expresiones explícitas para estas contribuciones individuales\(q\) en el caso más habitual de una molécula poliatómica no lineal:

Traslacional

\[q_t = \left(\frac{2\pi mkT}{\hbar^2}\right)^{\frac{3}{2}} V\]

donde\(\mu\) está la masa de la molécula y\(V\) es el volumen al que se limita su movimiento. Para las moléculas restringidas a una superficie de área\(A\), el resultado correspondiente es\(q_t = (2\pi mkT/\hbar^2)^{2/2} A\), y para las moléculas restringidas para moverse a lo largo de un solo eje sobre una longitud\(L\), el resultado es\(q_t = (2\pi mkT/\hbar^2)^{1/2} L\). Las magnitudes de estas funciones de partición se pueden calcular, utilizando\(\mu\) en amu,\(T\) en Kelvin\(L\), y\(A\), o\(V\) en cm, cm ² o cm ³, como

\[q_t = (3.28 \times10^{13} mT)^{\frac{1}{2},\frac{2}{2},\frac{3}{2}} L, A, V.\]

Claramente, la magnitud de\(q_t\) depende fuertemente del número de dimensiones en las que se mueve la molécula. Esto es el resultado de las vastas diferencias en las densidades de estado traslacional en las dimensiones 1, 2 y 3; recordemos que encontramos estos problemas de densidad de estado en el Capítulo 2.

Rotacional

\[q_{\rm rot} = \frac{\sqrt{\pi}}{\sigma} \sqrt{\frac{8\pi^2I_AkT}{\hbar^2} } \sqrt{\frac{8\pi^2I_BkT}{\hbar^2}} \sqrt{\frac{8\pi^2I_CkT}{\hbar^2}},\]

donde\(I_A\),\(I_B\), y\(I_C\) son los tres momentos principales de inercia de la molécula (es decir, valores propios del momento de inercia tensor). \(\sigma\)es el número de simetría de la molécula definido como el número de formas en que la molécula puede ser rotada en una configuración que es indistinguible de su configuración original. Por ejemplo,\(\sigma\) es 2 para\(H_2\) o\(D_2\), 1 para\(HD\), 3 para\(NH_3\), y 12 para\(CH_4\). Las magnitudes de estas funciones de partición se pueden calcular usando longitudes de enlace en Å y masas en amu y\(T\) en\(K\), usando

\[\sqrt{\frac{8\pi^2I_AkT}{\hbar^2} } = 9.75 \times10^6 \sqrt{I T}\]

Vibracional

\[q_{\rm vib} = \prod_{k=1}^{3N-6} \left\{\dfrac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)}\right\},\]

donde\(n_j\) está la frecuencia de la vibración\(j^{\rm th}\) armónica de la molécula, de la cual hay\(3N-6\). Si se quiere tratar las vibraciones a un nivel superior al armónico, esta expresión se puede modificar reemplazando las energías armónicas\(h\nu_j\) por expresiones de nivel superior.

Electrónica:

\[q_e = \sum_J \omega_J\exp\bigg(-\dfrac{\varepsilon_J}{kT}\bigg),\]

donde\(\varepsilon_J\) y\(\omega_J\) son las energías y degeneraciones del estado\(J^{\rm th}\) electrónico; la suma se lleva a cabo para aquellos estados para los que el producto\(\omega_J\exp\bigg(-\dfrac{\varepsilon_J}{kT}\bigg)\) es numéricamente significativo (es decir, niveles que cualquier población térmica significativa). Es convencional definir la energía de una molécula o ion con respecto a la de sus átomos. Entonces, el primer término en la función de partición electrónica suele escribirse como nosotros\(\exp(-D_e/kT)\), donde estamos la degeneración del estado electrónico básico y\(D_e\) es la energía requerida para disociar la molécula en sus átomos constituyentes, todo en sus estados electrónicos terrestres.

Observe que la magnitud de la función de partición traslacional es mucho mayor que la de la función de partición rotacional, la cual, a su vez, es mayor que la de la función vibracional. Además, tenga en cuenta que la función de partición traslacional tridimensional es mayor que la bidimensional, que es mayor que la unidimensional. Estos ordenamientos son simplemente reflejos del número promedio de estados cuánticos que son accesibles a los respectivos grados de libertad a la temperatura\(T\) que, a su vez, se relaciona con las separaciones energéticas y degeneraciones de estos estados.

La función de partición anterior y las ecuaciones termodinámicas forman la esencia de cómo la mecánica estadística proporciona las herramientas para conectar propiedades a nivel molecular como los niveles de energía y las degeneraciones, que finalmente determinan la\(E_j\) y la\(\Omega_j\), a las propiedades macroscópicas como \(\langle E\rangle \),\(\langle S\rangle \)\(\langle p\rangle \),\(\mu\),, etc.

Si se tiene un sistema para el que no se conocen los niveles de energía cuántica, puede ser posible expresar todas las propiedades termodinámicas en términos de la función de partición clásica, si el sistema pudiera describirse adecuadamente por la dinámica clásica. Esta función de partición se calcula evaluando la siguiente integral fase-espacio clásica (el espacio de fase es la colección de coordenadas\(q\) y momentos conjugados\(p\) como se discutió en el Capítulo 1)

\[Q = \frac{h^{-NM}}{N!} \int \exp \bigg(- \dfrac{H(q, p)}{kT}\bigg) dq dp.\]

En esta integral, se integra sobre las coordenadas internas (por ejemplo, longitudes y ángulos de enlace), orientacionales y traslacionales y momentos de las\(N\) moléculas. Si cada molécula tiene coordenadas\(K\) internas, 3 coordenadas de traducción y 3 coordenadas de orientación, el número total de tales coordenadas por molécula es\(M = K+6\). Entonces se pueden calcular todas las propiedades termodinámicas del sistema usando esto\(Q\) en lugar del cuántico\(Q\) en las ecuaciones dadas anteriormente para\(\langle E\rangle \)\(\langle p\rangle \),, etc.

Las funciones de partición clásicas discutidas anteriormente son especialmente útiles cuando están presentes interacciones intermoleculares sustanciales (y, por lo tanto, donde conocer los niveles de energía cuántica del sistema de\(N\) moléculas es altamente improbable). En tales casos, el hamiltoniano clásico a menudo se escribe en términos de los\(H^0\) cuales contiene todos los factores de energía cinética, así como todas las energías potenciales distintas de los potenciales intermoleculares, y el potencial intermolecular\(U\), que depende solo de un subconjunto de las coordenadas: \(H = H^0 + U\). Por ejemplo, supongamos que eso\(U\) depende únicamente de las distancias relativas entre las moléculas (es decir, de los grados de libertad\(3N\) traslacionales que denotamos\(r\)). Denotando todas las coordenadas restantes como\(y\), la integral de función de partición clásica se puede volver a expresar de la siguiente manera:

\[Q = \frac{h^{-NM}}{N!} \int \exp \bigg(- \dfrac{H^0(y, p)}{kT}\bigg) dy dp \int \exp \bigg(-\dfrac{U(r)}{kT}\bigg) dr.\]

El factor

\[Q_{\rm ideal} = \frac{h^{-NM}}{N!} \int \exp \bigg(- \dfrac{H^0(y, p)}{kT}\bigg) dy dp V^N\]

sería la función de partición si el hamiltoniano no\(H\) contenía interacciones intermoleculares\(U\). El\(V^N\) factor surge de la integración sobre todas las coordenadas traslacionales si\(U(r)\) está ausente. El otro factor

\[Q_{\rm inter} = \frac{1}{V^N} {\int \exp \bigg(-\dfrac{U(r)}{kT}\bigg) dr}\]

contiene todos los efectos de las interacciones intermoleculares y reduce a la unidad si el potencial\(U\) desaparece. Si, como supone el ejemplo aquí considerado,\(U\) solo depende de las posiciones de los centros de masa de las moléculas (es decir, no de orientaciones moleculares o geometrías internas), la función de\(Q_{\rm ideal}\) partición se puede escribir en términos de la traslación molecular, rotacional y vibracional funciones de partición mostradas anteriormente:

\[Q_{\rm ideal} = \frac{1}{N!} \bigg[\left(\frac{2\pi mkT}{\hbar^2}\right)^{\frac{3}{2}} V \frac{\sqrt{\pi}}{\sigma} \sqrt{\frac{8\pi^2I_AkT}{\hbar^2} } \sqrt{\frac{8\pi^2I_BkT}{\hbar^2}} \sqrt{\frac{8\pi^2I_CkT}{\hbar^2}} \]

\[\prod_{k=1}^{3N-6} \left\{\frac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)}\right\} \sum_J \omega_J\exp\left(\frac{-\varepsilon_J}{kT}\right)\bigg]^N .\]

Debido a que todas las ecuaciones que relacionan las propiedades termodinámicas con las funciones de partición contienen\(\ln Q\), todas esas propiedades se descompondrán en una suma de dos partes, una proveniente\(\ln Q_{\rm ideal}\) y otra proveniente de\(\ln Q_{\rm inter}\). Este último contiene todos los efectos de las interacciones intermoleculares. Esto quiere decir que, en este caso de la mecánica clásica, todas las ecuaciones termodinámicas pueden escribirse como un componente ideal más una parte que surge de las fuerzas intermoleculares. Nuevamente, el texto de Mecánica Estadística de McQuarrie es una buena fuente para leer más detalles sobre estos temas.

Constantes de equilibrio en términos de funciones de partición

Una de las aplicaciones más importantes y útiles de la termodinámica estadística surge en la relación que da la constante de equilibrio de una reacción química o para una transformación física (por ejemplo, adsorción de moléculas sobre una superficie metálica o sublimación de moléculas a partir de un cristal) en términos de funciones de partición. Específicamente, para cualquier equilibrio químico o físico (por ejemplo, el primero podría ser el\(HF \rightleftharpoons H^+ + F^-\) equilibrio; el segundo podría ser\(H_2O(l) \rightleftharpoons H_2O(g)\)), se puede relacionar la constante de equilibrio (expresada en términos de números de moléculas por unidad de volumen o por unidad de área, dependiendo de si las especies se someten a traslación movimiento en 3 o 2 dimensiones) en términos de las funciones de partición de estas moléculas. Por ejemplo, en el hipotético equilibrio químico\(A + B \rightleftharpoons C\), se\(K\) puede escribir la constante de equilibrio, si la especie puede tratarse como que tiene potenciales intermoleculares insignificantemente débiles, como:

\[K = \dfrac{(N_C/V)}{(N_A/V) (N_B/V)} = \frac{(q_C/V)}{(q_A/V) (q_B/V)}.\]

Aquí,\(q_J\) es la función de partición para moléculas de tipo\(J\) confinadas a volumen\(V\) a temperatura\(T\). Como otro ejemplo considere la reacción de isomerización que involucra las formas normales (N) y zwitteriónicas (Z) de arginina que fueron discutidas en el Capítulo 5. Aquí, la constante de equilibrio pertinente sería:

\[K = \frac{(N_Z/V)}{(N_N/V)} = \frac{(q_Z/V)}{(q_N/V)}.\]

Entonces, si se pueden evaluar las funciones de partición\(q\) para las moléculas de reactivo y producto en términos de los niveles de energía traslacional, electrónica, vibracional y rotacional de estas especies, se puede expresar la constante de equilibrio en términos de estas propiedades a nivel de molécula.

Observe que las expresiones constantes de equilibrio anteriores equivalen a proporciones de concentraciones de especies (en, números de moléculas por unidad de volumen) a relaciones de funciones de partición correspondientes por unidad de volumen. Debido a que las funciones de partición son un recuento del número de estados cuánticos disponibles para el sistema (es decir, la densidad promedio de los estados cuánticos), esto significa que equiparamos las densidades numéricas de especies con las densidades de estado cuántico cuando usamos las expresiones anteriores para la constante de equilibrio. En otras palabras, la mecánica estadística produce constantes de equilibrio relacionadas con números de moléculas (es decir, densidades numéricas) no concentraciones molales o molales.

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

• Integrated by Tomoyuki Hayashi (UC Davis)