7.2: Monte Carlo Evaluación de Propiedades

Una herramienta que ha demostrado ser extremadamente poderosa en mecánica estadística desde que las computadoras se volvieron lo suficientemente rápidas como para permitir simulaciones de sistemas complejos es el método Monte Carlo (MC). Este método permite evaluar las integraciones que aparecen en la función de partición clásica descrita anteriormente generando una secuencia de configuraciones (es decir, ubicaciones de todas las moléculas en el sistema así como de todas las coordenadas internas de estas moléculas) y asignando un factor de ponderación a estas configuraciones. Al introducir una forma especialmente eficiente de generar configuraciones que tienen una alta ponderación, el método MC nos permite simular sistemas extremadamente complejos que pueden contener millones de moléculas.

Para apreciar por qué es útil tener una herramienta como MC, consideremos cómo se podría escribir un programa de computadora para evaluar la función de partición clásica

\[Q = \frac{h^{-NM}}{N!} \int \exp (- H(q, p)/kT)\,dq \,dp\]

Para un sistema que consiste en átomos de\(N\) Ar en una caja de volumen\(V\) a temperatura T. El hamiltoniano clásico\(H(q,p)\) consiste en una suma de energías potenciales cinéticas e interatómicas

\[H(p,q)=\sum_{i=1}^N\frac{p_i^2}{2m}+V(q)\]

La integración sobre las variables de\(3N\) momentum se puede llevar a cabo analíticamente y\(Q\) permite escribirse como

\[Q=\frac{1}{N!}\left(\frac{2\pi mkT}{\hbar^2}\right)^{3N/2}\int \exp\left[-\frac{V(q_1,q_2,\cdots,q_{3N})}{kT}\right]dq_1dq_2\cdots dq_{3N-1}\]

La contribución a\(Q\) proporcionada por la integral sobre las coordenadas a menudo se denomina función de partición configuracional

\[Q_{\rm config}=\int \exp\left[-\frac{V(q_1,q_2,\cdots,q_{3N})}{kT}\right]dq_1dq_2\cdots dq_{3N-1}\]

Si la densidad de los átomos de\(N\) Ar es alta, como en estado líquido o sólido, el potencial\(V\) dependerá de las\(3N\) coordenadas de los átomos de Ar de una manera que no permita realizar aproximaciones adicionales sustanciales. Por lo tanto, uno se enfrentaría a evaluar una integral sobre coordenadas\(3N\) espaciales de una función que depende de todas estas coordenadas. Si uno fuera a discretizar cada uno de los ejes de\(3N\) coordenadas usando digamos\(K\) puntos a lo largo de cada eje, la evaluación numérica de esta integral como una suma sobre las\(3N\) coordenadas requeriría un escalado de esfuerzo computacional como K3N. Incluso para 10 átomos de Ar teniendo cada eje\(K\) = 10 puntos, esto es del orden de 1030 operaciones informáticas. Claramente, sería una tontería emprender una evaluación tan directa de esta integral clásica.

El procedimiento MC permite evaluar tales integrales de alta dimensión mediante

1. no dividir cada uno de los\(3N\) ejes en puntos\(K\) discretos, sino más bien
2. seleccionar valores\(q_1, q_2, \cdots q_{3N}\) para los cuales el integrando no\(\exp(-V/kT)\) es despreciable, mientras que también
3. evitando valores\(q_1, q_2, \cdots q_{3N}\) para los que el integrando\(\exp(-V/kT)\) es lo suficientemente pequeño como para descuidar.

Para entonces sumando solo valores\(q_1, q_2, \cdots q_{3N}\) que cumplan con estos criterios, el proceso MC puede estimar la integral. Por supuesto, la magia radica en cómo se diseña un algoritmo riguroso y computacionalmente eficiente para seleccionar aquellos\(q_1, q_2, \cdots q_{3N}\) que cumplan con los criterios.

Para ilustrar cómo funciona el proceso MC, consideremos la realización de una simulación MC representativa del agua líquida a cierta densidad r y temperatura T. Se inicia colocando moléculas de\(N\) agua en una caja de volumen\(V\) elegida de tal manera que\(N/V\) reproduce la densidad especificada. Para efectuar el proceso MC, debemos suponer que la energía potencial total (intramolecular e intermolecular)\(V\) de estas moléculas de\(N\) agua puede calcularse para cualquier disposición de las\(N\) moléculas dentro de la caja y para cualquier valor de las longitudes de enlace interno y ángulos del agua moléculas. Observe que, como mostramos anteriormente al considerar el ejemplo de Ar,\(V\) no incluye la energía cinética de las moléculas; es solo la energía potencial. A menudo, esta energía\(V\) se expresa como una suma de contribuciones intramoleculares de estiramiento y flexión del enlace, una para cada molécula, más un potencial intermolecular aditivo por pares:

\[V = \sum_J V_{\rm (internal)}{}_J + \sum_{J,K} V_{\rm (intermolecular)}{}_{J,K},\]

aunque el proceso MC no requiere que se emplee tal descomposición; la energía\(V\) podría calcularse de otras maneras, si procede. Por ejemplo,\(V\) podría evaluarse como la energía Born-Oppenheimer si fuera factible un cálculo de la estructura electrónica ab initio en el sistema de\(N\) moléculas completas. El proceso MC no depende de cómo\(V\) se compute, sino que, más comúnmente, se evalúa como se muestra arriba.

Metrópolis Montecarlo

En cada etapa del proceso MC, esta energía potencial\(V\) se evalúa para las posiciones actuales de las moléculas de\(N\) agua. En su implementación más común y sencilla conocida como el proceso de Metropolis Montecarlo, se elige entonces una sola molécula de agua al azar y una de sus coordenadas internas (longitudes de enlace o ángulo) o externas (posición u orientación) se selecciona al azar. Esta coordenada (q) se altera entonces en una pequeña cantidad (\(q \rightarrow q+\delta q;ta{q}\)) y la energía potencial\(V\) se evalúa en la nueva configuración (\(q+\delta q\)). La cantidad\(\delta{q}\) por la que se varían las coordenadas suele elegirse para hacer la fracción de pasos MC que se aceptan (siguiendo el procedimiento que se detalla a continuación) aproximadamente 50%. Esto se ha demostrado para optimizar el rendimiento del algoritmo MC.

Al implementar el proceso MC, suele ser importante considerar cuidadosamente cómo se definen las coordenadas\(q\) que se utilizarán para generar los pasos MC. Por ejemplo, en el caso de los átomos de\(N\) Ar discutidos anteriormente, podría ser aceptable usar las coordenadas\(3N\) cartesianas de los\(N\) átomos. Sin embargo, para el ejemplo del agua, sería muy ineficiente emplear las coordenadas\(9N\) cartesianas de las moléculas de\(N\) agua. El desplazamiento de, por ejemplo, uno de los\(H\) átomos a lo largo del eje x mientras se mantienen todas las demás coordenadas fijas alteraría la energía del enlace O-H intramolecular y la energía de flexión H-O-H, así como las energías de enlace de hidrógeno intermoleculares a las moléculas de agua vecinas. Los cambios de energía intramoleculares probablemente serían muy superiores\(kT\) a menos que se\(\delta q\) empleara un cambio de coordenadas muy pequeño. Debido a que es importante para la eficiencia del proceso MC realizar desplazamientos\(\delta q\) que produzcan aproximadamente 50% de aceptación, es mejor, para el caso del agua, hacer uso de coordenadas como el centro de masa y las coordenadas de orientación de las moléculas de agua (para lo cual los desplazamientos mayores producen energía cambios dentro de unos pocos\(kT\)) y desplazamientos menores de las coordenadas de estiramiento O-H y flexión H-O-H (para mantener el cambio de energía dentro de unos pocos\(kT\)).

Otro punto a hacer acerca de cómo se suele utilizar el proceso MC es que, cuando la energía intermolecular es aditiva por pares, la evaluación del cambio de energía que\(V(q+\delta q) – V(q) = \delta V\) acompaña al cambio en\(q\) requiere un esfuerzo computacional que es proporcional al número\(N\) de moléculas en el sistema porque sólo es necesario computar aquellos factores\(V_{\rm (intermolecular)}{}_{J,K}\), con\(J\) o\(K\) iguales a la única molécula que se desplaza. Esta es la razón por la que a menudo\(V\) se emplean formas aditivas de pares para.

Volvamos ahora a cómo se implementa el proceso MC. Si el cambio de energía\(\delta V\) es negativo (es decir, si la energía potencial es disminuida por el desplazamiento de coordenadas), se permite que\(\delta q\) se produzca el cambio en las coordenadas y la nueva configuración resultante se cuente entre las configuraciones aceptadas por MC. Por otro lado, si\(\delta V\) es positivo, el paso de\(q\) a no\(q + \delta q\) es simplemente rechazado (hacerlo produciría un algoritmo dirigido a encontrar un mínimo en el paisaje energético, que no es el objetivo). En cambio, la cantidad\(P = \exp(-\delta V/kT)\) se utiliza para calcular la probabilidad de aceptar este movimiento de aumento de energía. En particular, se selecciona un número aleatorio entre, por ejemplo, 0.000 y 1.000. Si el número aleatorio es mayor que\(P\) (expresado en el mismo formato decimal), entonces se rechaza el movimiento. Si el número aleatorio es menor que\(P\), se acepta el movimiento y se incluye la nueva ubicación entre el conjunto de configuraciones aceptadas por MC. Luego, se elige al azar nueva molécula de agua y su coordenada interna o externa y se repite todo el proceso.

De esta manera, se genera una secuencia de movimientos aceptados por MC que representan una serie de configuraciones para el sistema de moléculas de\(N\) agua. En ocasiones esta serie de configuraciones se llama trayectoria de Monte Carlo, pero es importante darse cuenta de que no hay dinámica ni información de tiempo en esta serie. Se ha demostrado que este conjunto de configuraciones es adecuadamente representativo de las geometrías que experimentará el sistema a medida que se mueva en equilibrio a la temperatura especificada\(T\) (n.b.,\(T\) es la única forma en que la información sobre la energía cinética de las moléculas ingresa al proceso MC), pero no hay tiempo ni atributos dinámicos contenidos en él.

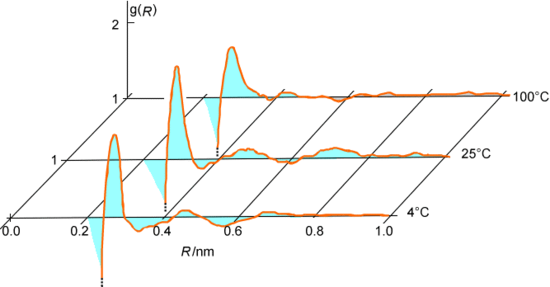
A medida que se genera la serie de pasos aceptados, se puede realizar un seguimiento de varios datos geométricos y energéticos para cada configuración aceptada. Por ejemplo, se pueden monitorear las distancias R entre todos los pares de átomos de oxígeno en el sistema de agua que se está discutiendo y luego promediar estos datos en todos los pasos aceptados para generar una función de distribución radial oxígeno-oxígeno\(g(R)\) como se muestra en la Figura 7.3. Alternativamente, se podrían acumular las energías de interacción intermolecular entre pares de moléculas de agua y promediarlas sobre todas las configuraciones aceptadas para extraer la energía cohesiva del agua líquida.

Figura 7.3. La distribución radial funciona entre pares de átomos de oxígeno en H2O a tres temperaturas diferentes.

El procedimiento MC también nos permite calcular el promedio de equilibrio de cualquier propiedad\(A(q)\) que dependa de las coordenadas de las\(N\) moléculas. Tal promedio se escribiría en términos de la función normalizada de distribución de probabilidad de coordenadas\(P(q)\) como:

\[\langle A \rangle = \int P(q)A(q) dq = \dfrac{\int \exp(-\beta V(q))A(q)dq}{\int \exp(-\beta V(q))dq}\]

El denominador en la definición de\(P(q)\) es, por supuesto, proporcional a la coordenada-contribución a la función de partición\(Q\). En el proceso MC, este promedio se calcula formando la siguiente suma sobre las M configuraciones aceptadas por MC\(q_J\):

\[\langle A \rangle =\frac{1}{M}\sum_{J=1}^M A(q_J)\]

En la mayoría de las simulaciones MC, millones de pasos aceptados contribuyen a los promedios anteriores. A primera vista, puede parecer que una cantidad tan grande de pasos representan una carga computacional extrema. Sin embargo, recordemos que la discretización directa de los\(3N\) ejes produjo un resultado cuyo esfuerzo se escaló como\(K^{3N}\), lo cual es inviable incluso para pequeñas cantidades de moléculas

Entonces, ¿por qué funcionan las simulaciones MC cuando falla la forma sencilla? Es decir, ¿cómo se pueden manejar miles o millones de coordenadas cuando el análisis anterior sugeriría que realizar una integral sobre tantas coordenadas requeriría\(K^{3N}\) cálculos? Lo principal a entender es que la discretización\(K\) -sitio de las\(3N\) coordenadas es una forma estúpida de realizar la integral anterior porque hay muchos (de hecho, la mayoría) valores de coordenadas donde el valor de la cantidad A cuyo promedio se quiere multiplicar por\(\exp(-\beta V)\) es despreciable. Por otro lado, el algoritmo MC está diseñado para seleccionar (como pasos aceptados) aquellas coordenadas para las cuales no\(\exp(-\beta V)\) es despreciable. Entonces, evita configuraciones que son estúpidas y se enfoca en aquellas para las que el factor de probabilidad es mayor. ¡Por eso funciona el método MC!

La variante estándar de Metrópolis del procedimiento MC fue descrita anteriormente donde se\(\delta q\) dieron sus reglas para aceptar o rechazar desplazamientos de coordenadas de ensayo. Existen varias otras formas de definir reglas para aceptar o rechazar los desplazamientos de coordenadas MC de ensayo, algunas de las cuales implican el uso de información sobre las fuerzas que actúan sobre las coordenadas, todas las cuales pueden mostrarse para generar una serie de configuraciones aceptadas por MC consistentes con un sistema de equilibrio. El libro Computer Simulations of Liquids, M. P. Allen y D. J. Tildesley, Oxford U. Press, Nueva York (1997) proporciona buenas descripciones de estas alternativas al método Metrópolis MC, por lo que aquí no voy a profundizar en estos enfoques.

Muestreo de paraguas

Resulta que el procedimiento MC descrito anteriormente es un método altamente eficiente para computar integrales multidimensionales de la forma

\[\int P(q) A(q) dq\]

donde\(P(q)\) es una distribución de probabilidad normalizada (positiva) y\(A(q)\) es cualquier propiedad que dependa de la variable multidimensional q.

Sin embargo, hay casos en los que este enfoque convencional de MC necesita ser modificado mediante el uso del llamado muestreo paraguas. Para ilustrar cómo se hace esto y por qué se necesita, supongamos que se quería utilizar el proceso MC para calcular un promedio, con\(\exp(-\beta V(q))\) como factor de ponderación, de una función\(A(q)\) que es grande siempre que dos o más moléculas tengan potenciales intermoleculares altos (es decir, repulsivos). Por ejemplo, uno podría haber

\[A(q) = \sum_{I<J} \frac{a}{|\textbf{R}_I- \textbf{R}_J|^n}.\]

Tal función podría, por ejemplo, ser utilizada para monitorear cuando pares de moléculas, con coordenadas de centro de masa RJ y RI, se acercan lo suficientemente cerca como para sufrir una reacción que requiera que superen una barrera intermolecular alta.

El problema con el uso de métodos MC convencionales para calcular

\[\langle A \rangle = \int A(q) P(q) dq\]

en tales casos es que

1. i.\(P(q) = \dfrac{\exp(-\beta V(q))}{\int \exp(-\beta V)dq}\) favorece aquellas coordenadas para las que la energía potencial total\(V\) es baja. Entonces, las coordenadas con alto\(V(q)\) son muy poco aceptadas.
2. ii. Sin embargo,\(A(q)\) está diseñado para identificar eventos en los que pares de moléculas se acercan de cerca y así tienen\(V(q)\) valores altos.

Entonces, hay una competencia entre\(P(q)\) y\(A(q)\) que hace que el procedimiento MC sea ineficaz en tales casos porque el promedio que se quiere computar involucra el producto\(A(q) P(q)\) que es pequeño para la mayoría de los valores de q.

Lo que se hace para superar esta competencia es introducir una llamada función de ponderación paraguas\(U(q)\) que

1. i. alcanza los valores más grandes donde\(A(q)\) es grande, y
2. ii. es positivo y toma valores entre 0 y 1 por lo que se puede usar como se muestra a continuación para definir una función de ponderación de probabilidad adecuada.

Luego, uno reemplaza\(P(q)\) en el algoritmo MC por el producto\(P(q)U(q)\) y lo usa como función de ponderación. Para ver cómo funciona este reemplazo, reescribimos el promedio que debe calcularse de la siguiente manera:

\[\langle A \rangle = \int P(q)A(q) dq = \dfrac{\int \exp(-\beta V(q))A(q)dq}{\int \exp(-\beta V(q))dq}\]

\[=\dfrac{\dfrac{ \int U(q)\exp(-\beta V(q))(A(q)/U(q)) dq }{\int U(q)\exp(-\beta V(q)) dq}}{\dfrac{ \int U(q)\exp(-\beta V(q))(1/U(q)) dq}{ \int U(q)\exp(-\beta V(q)) dq}}=\dfrac{\Big\langle \dfrac{A}{U}\Big\rangle_{Ue^{-\beta UV}}}{\Big\langle \dfrac{1}{U}\Big\rangle_{Ue^{-\beta V}}}\]

La interpretación de la última identidad es que\(\langle A \rangle \) puede ser computada por

1. i. utilizar el proceso MC para evaluar el promedio de (\(A(q)/U(q)\)) pero con un factor de ponderación de probabilidad de\(U(q) \exp(-\beta V(q))\) aceptar o rechazar cambios de coordenadas, y
2. ii. también utilizando el proceso MC para evaluar el promedio de (\(1/U\)(q)) nuevamente con\(U(q) \exp(-\beta V(q))\) como factor de ponderación, y finalmente
3. iii. tomando el promedio de (\(A/U\)) dividido por el promedio de (\(1/U\)) para obtener el resultado final.

El secreto del éxito del muestreo de paraguas es que el producto

\(U(q) \exp(-\beta V(q))\)hace que el proceso MC enfatice en su procedimiento de aceptación y rechazo las coordenadas para las cuales ambos\(\exp(-\beta V)\) y\(U\) (y por lo tanto\(A\)) son significativos. Por supuesto, la compensación es que las cantidades (\(A/U\)y\(1/U\)) cuyos promedios se\(U(q) \exp(-\beta V(q))\) computan usando como la función de ponderación MC son en sí mismas susceptibles de ser muy pequeñas en coordenadas\(q\) donde la función de ponderación es grande. Consideremos algunos ejemplos de cuándo y cómo uno podría querer usar técnicas de muestreo paraguas.

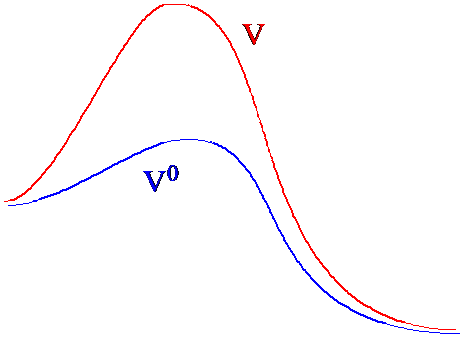
Supongamos que se tiene un sistema para el cual la evaluación de la función de partición (y por lo tanto de todas las propiedades termodinámicas) se puede llevar a cabo con un esfuerzo computacional razonable y otro sistema similar (es decir, uno cuyo potencial no difiera mucho del primero) para lo cual esta tarea es muy difícil. Llamemos a la función potencial del primer sistema\(V^0\) y a la del segundo sistema\(V^0 + \Delta V\). La función de partición de este último sistema se puede escribir de la siguiente manera

\[Q=\sum_J \exp(-\beta (V^0+\Delta V))=Q^0 \sum_J \exp(-\beta(V^0+\Delta V))/Q^0=Q^0\langle \exp(-\beta(V^0+\Delta V))\rangle^0\]

donde\(Q^0\) es la función de partición del primer sistema y es el promedio conjunto de la cantidad tomada con respecto al conjunto apropiado al primer sistema. Este resultado sugiere que se puede formar la relación de las funciones de partición (\(Q/Q^0\)) calculando el promedio de conjunto de usar la función de ponderación del primer sistema en el proceso MC. Así mismo, para calcular, para segundo sistema, el valor promedio de cualquier propiedad\(A(q)\) que dependa únicamente de las coordenadas de las partículas, se puede proceder de la siguiente manera

\[\langle A \rangle=\dfrac{\sum_J A_J\exp(-\beta(V^0+\Delta V)) }{Q}=\frac{Q^0}{Q}\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0\]

donde es el promedio conjunto de la cantidad\(A\) tomada con respecto al conjunto apropiado al primer sistema. Usando el resultado derivado anteriormente para la ratio (\(Q/Q^0\)), esta expresión para se\(\langle A \rangle \) puede reescribir como

\[\langle A \rangle=\frac{Q^0}{Q}\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0=\dfrac{\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0}{\langle \exp(-\beta(V^0+\Delta V)) \rangle^0}.\]

En esta forma, se nos instruye para formar el promedio de\(A\exp(-\beta(V^0+\Delta V))\) para el segundo sistema por

1. a. formar el promedio de conjunto de usar la función de ponderación para el primer sistema,
2. b. formar el promedio de conjunto de usar la función de ponderación para el primer sistema, y
3. c. tomando la proporción de estos dos promedios.

Esto es exactamente lo que el dispositivo de muestreo de paraguas nos dice que hagamos si tuviéramos que elegir como función paraguas

\[U=\exp(\beta \Delta V).\]

En este ejemplo, el paraguas está relacionado con la diferencia en las energías potenciales de los dos sistemas cuya relación deseamos explotar.

¿En qué circunstancias sería útil este tipo de enfoque? Supongamos que uno estuviera interesado en realizar un promedio MC de una propiedad para un sistema cuyo paisaje energético\(V(q)\) tiene muchos mínimos locales separados por grandes barreras energéticas, y supongamos que era importante muestrear configuraciones que caracterizan los muchos mínimos locales en el muestreo. Un cálculo sencillo de MC usando\(\exp(-\beta V)\) como función de ponderación probablemente fallaría porque una secuencia de desplazamientos de coordenadas de cerca de un mínimo local a otro mínimo local tendría muy pocas posibilidades de ser aceptados en el proceso MC porque las barreras son muy altas. Como resultado, el promedio MC probablemente generaría configuraciones representativas de solo la existencia de equilibrio del sistema cerca de un mínimo local en lugar de representativas de su exploración del paisaje energético completo.

Sin embargo, si se pudieran identificar aquellas regiones de espacio de coordenadas en las que se producen barreras altas y construir una función\(\Delta V\) que sea grande y positiva solo en esas regiones, entonces se podría usar

\[U=\exp(\beta \Delta V).\]

como la función paraguas y calcular promedios para el sistema que tiene potencial\(V(q)\) en términos de promedios conjuntos para un sistema modificado cuyo potencial\(V_0\) es

\[V^0=V-\Delta V\]

En la Figura 7. 3a, ilustro cómo los paisajes potenciales originales y modificados difieren en regiones entre dos mínimos locales.

Figura 7.3 a. Representación cualitativa del potencial\(V\) para un sistema que tenga una gran barrera y para el sistema modificado con paraguas con potencial\(V^0 = V-\Delta V\).

Las coordenadas aceptadas por MC generadas usando el potencial modificado\(V^0\) muestrearían los diversos mínimos locales y así todo el paisaje de una manera mucho más eficiente porque no quedarían atrapadas por las grandes barreras energéticas. Mediante el uso de estas coordenadas aceptadas por MC, se puede estimar el valor promedio de una propiedad\(A\) apropiada al potencial\(V\) que tiene las grandes barreras haciendo uso de la identidad.

\[\langle A \rangle=\frac{Q^0}{Q}\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0=\dfrac{\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0}{\langle \exp(-\beta(V^0+\Delta V)) \rangle^0}.\]

La estrategia paraguas anterior podría ser útil para generar un buen muestreo de configuraciones características de los muchos mínimos locales, lo que sería especialmente beneficioso si la cantidad\(A(q)\) enfatizara esas configuraciones. Este sería el caso, por ejemplo, si\(A(q)\) se midieran las distancias interatómicas de oxígeno-hidrógeno intramoleculares y vecinas más cercanas en una simulación MC de agua líquida. Por otro lado, si se quiere utilizar como\(A(q)\) medida de la energía necesaria para que un\(Cl^-\) ion sufra, en una solución acuosa 1 M de NaCl, un cambio en el número de coordinación de 6 a 5 como se ilustra en la Figura 7.3 b, se necesitaría un muestreo que sea preciso tanto cerca de los mínimos locales correspondientes a la coordenada 5 y 6 y a las estructuras de estado de transición.

Figura 7.3 b Representación cualitativa de\(Cl^-\) iones de 5 y 6 coordenadas en agua y del perfil energético que conecta estas dos estructuras.

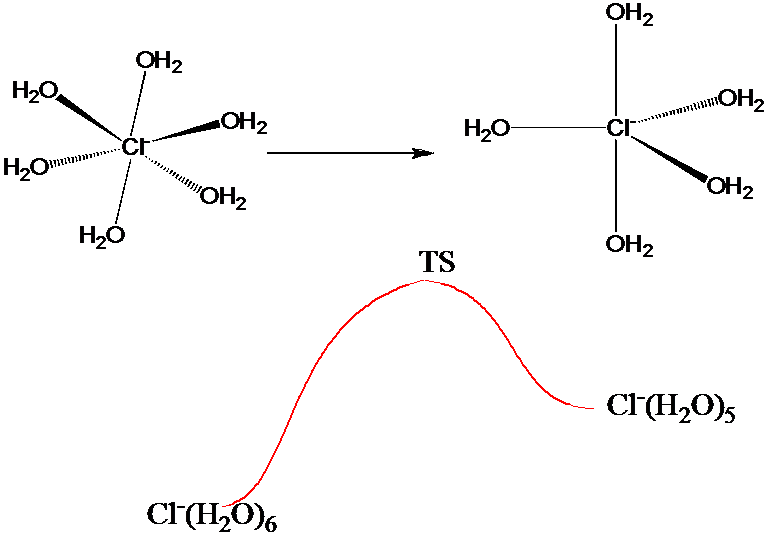
Usar una función paraguas similar a la discutida anteriormente para simplemente bajar la barrera que conecta las dos estructuras de\(Cl^-\) iones puede no ser suficiente. Aunque esto permitiría muestrear ambos mínimos locales, su muestreo de estructuras cercanas al estado de transición sería cuestionable si la cantidad\(\Delta V\) en la que se baja la barrera (para permitir que los pasos MC que se mueven sobre la barrera sean aceptados con una probabilidad no despreciable) es grande. En tales casos, es prudente emplear una serie de paraguas para conectar los mínimos locales con los estados de transición.

Suponiendo que uno tiene conocimiento de las energías y geometrías de solvatación local que caracterizan los dos mínimos locales y el estado de transición, así como una suposición o aproximación razonable de la ruta de reacción intrínseca (refiérase de nuevo a la Sección 3.3 del Capítulo 3) que conecta estas estructuras, se procede de la siguiente manera a generar una serie de las llamadas ventanas dentro de cada una\(A\) de las cuales se evalúa la energía libre del\(Cl^-\) ion solvatado.

1. 1. Usando todo el potencial\(V\) del sistema para constituir la función de ponderación inalterada\(\exp(-\beta V(q))\), se multiplica esto por una función paraguas\[U(q)=\dfrac{0;\{s_1-\delta/2\le s(q)\le s_1+\delta/2\}}{\infty;{\rm otherwise}}\]
   para formar la función de ponderación alterada en el paraguas\(U(q) \exp(-\beta V(q))\). En U (q), s (q) es el valor del valor de la coordenada de reacción intrínseca IRC evaluada para la geometría actual del sistema q,\(s_1\) es el valor del IRC que caracteriza la primera ventana, y d es el ancho de esta ventana. La primera ventana podría, por ejemplo, corresponder a geometrías cercanas al mínimo local de 6 coordenadas de la estructura de\(Cl^-\) iones solvatados. El ancho de cada ventana d debe elegirse de manera que la variación de energía dentro de la ventana no sea superior a 1-2 kT; de esta manera, el proceso MC tendrá una buena fracción de aceptación (es decir, ca. 50%) y las configuraciones generadas permitirán fluctuaciones de energía cuesta arriba hacia el TS de aproximadamente esta cantidad.
2. 2. Como el proceso MC se realiza usando la\(U(q) \exp(-\beta V(q))\) ponderación anterior, se construye un histograma\(P_1(s)\) para la frecuencia con la que el sistema alcanza varios valores s a lo largo del IRC. Por supuesto, la severa ponderación causada por no\(U(q)\) permitirá que el sistema realice ningún valor de s fuera de la ventana.
3. 3. Luego se crea una segunda ventana que se conecta a la primera ventana (es decir, con\(s_1+\delta/2 = s_2 - \delta/2\)) y repite el muestreo MC usando\[U(q)=\dfrac{0;\{s_2-\delta/2\le s(q)\le s_2+\delta/2\}}{\infty;{\rm otherwise}}\]
   para generar un segundo histograma\(P_2(s)\) para la frecuencia con la que el sistema alcanza varios valores de s a lo largo del IRC dentro de la segunda ventana.
4. 4. Este proceso se repite en una serie de ventanas conectadas\(\{s_k-\delta/2\le s(q)\le s_k+\delta/2\}\)

cuyos centros\(s_k\) van desde el\(Cl^-\) ion de 6 coordenadas (\(k = 1\)), pasando por el estado de transición (\(k = TS\)), y hasta el\(Cl^-\) ion de 5 coordenadas (\(k = N\)).

Después de realizar esta serie de muestreos\(N\) alterados con paraguas, se tiene en la mano una serie de\(N\) histogramas {\(P_k(s); k = 1, 2, \cdots TS, \cdots N\)}. Dentro de la\(k^{\rm th}\) ventana,\(P_k(s)\) da la probabilidad relativa de que el sistema esté en un punto s a lo largo del IRC. Para generar la función de probabilidad absoluta normalizada P (s) expresando la probabilidad de estar en un punto s, se puede proceder de la siguiente manera:

1. Debido a que la primera y segunda ventanas están conectadas en el punto\(s_1+\delta/2 = s_2 - \delta/2\), se puede escalar\(P_2(s)\) (es decir, multiplicarla por una constante) para que coincida\(P_1(s)\) en este punto común para producir una nueva\(P'_2(s)\) función

\[P'_2(s)=P_2(s)\dfrac{P_1(s_1+\delta/2)}{P_2(s_2-\delta/2)}\]

Esta nueva función describe exactamente la misma probabilidad relativa dentro de la segunda ventana, pero, a diferencia\(P_2(s)\), se conecta suavemente a\(P_1(s)\).

2. Debido a que la segunda y tercera ventanas están conectadas en el punto\(s_2+\delta/2 = s_3 - \delta/2\), se puede escalar\(P_3(s)\) para que coincida en este punto común para producir una nueva función

\[P'_3(s)=P_3(s)\dfrac{P'_2(s_2+\delta/2)}{P_3(s_3-\delta/2)}\]

3. Este proceso de escalado\(P_k\) para que coincida en\(s_k – \delta/2 = s_{k-1} + \delta/2\) se repite hasta que la ventana final\(k = N-1\) se conecta a\(k = N\). Al completar esta serie de conexiones, se tiene en la mano una función de probabilidad continua\(P(s)\), que puede normalizarse

\[P_{\rm normalized}=\frac{P(s)}{\int_{s=0}^{s_{\rm final}}P(s)ds }\]

De esta manera, se puede calcular la probabilidad de acceder al TS\(P_{\rm normalized}(s=TS)\), y el perfil de energía libre

\[A(s)=-kT\ln P_{\rm normalized}(s)\]

en cualquier punto a lo largo del IRC. Es mediante el uso de una serie de ventanas conectadas, dentro de cada una de las cuales el proceso MC muestrea estructuras cuyas energías pueden fluctuar en 1-2\(kT\), que se genera una conexión suave de geometrías de baja energía a alta energía (por ejemplo, TS).

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

• Integrated by Tomoyuki Hayashi (UC Davis)