7.5: Algunas Aplicaciones Importantes de la Mecánica Estadística

En esta Sección, presento varias aplicaciones de la mecánica estadística que son importantes para que los estudiantes sean conscientes porque surgen frecuentemente cuando los químicos hacen uso de las herramientas de la mecánica estadística. Estos ejemplos incluyen

1. Las ecuaciones básicas conectan las propiedades traslacionales, rotacionales, vibracionales y electrónicas de las moléculas aisladas (es decir, en fase gaseosa) con su termodinámica.
2. Las descripciones más básicas de las vibraciones de iones, átomos o moléculas dentro de los cristales.
3. Los modelos más elementales para describir el comportamiento cooperativo y las transiciones de fase en sistemas gas-superficie y líquido-líquido.
4. Las contribuciones de las fuerzas intermoleculares a la termodinámica de los gases.

Termodinámica de moléculas de gas

Las ecuaciones que relacionan las variables termodinámicas con las funciones de partición molecular se pueden emplear para obtener las siguientes expresiones para la energía\(E\), capacidad calorífica\(C_V\), energía libre de Helmholz\(A\), entropía\(S\) y potencial químico\(\mu\) en el caso de un gas (es decir, en ausencia de interacciones intermoleculares) de moléculas poliatómicas:

\[\dfrac{E}{NkT} = \dfrac{3}{2} + \dfrac{3}{2} + \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \dfrac{h\nu_J/kT} {\exp(h\nu_J/kT)-1} \right] – \dfrac{D_e}{kT},\]

\[\dfrac{C_V}{Nk} = \dfrac{3}{2} + \dfrac{3}{2} + \sum_{J=1}^{3N-6} \left(\dfrac{h\nu_J}{kT}\right)^2 \dfrac{\exp(h\nu_J/kT)}{(\exp(h\nu_J/kT)-1)^2} ,\]

\[-\dfrac{A}{NkT} = \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{V_e}{N}\right) + \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]

\[ - \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] + \dfrac{D_e}{kT} + \ln\omega_e\]

\[\dfrac{S}{Nk} = \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{V_e^{5/2}}{N}\right) + \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]

\[ + \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J/kT} {\exp(h\nu_J/kT)-1} – \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] + \ln\omega_e\]

\[\dfrac{\mu}{kT} = - \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{kT}{p}\right) - \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]

\[ + \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] - \dfrac{D_e}{kT} - \ln\omega_e.\]

Anteriormente en este Capítulo en la Sección 7.1.2, mostramos cómo se derivan estas ecuaciones, por lo que remito al lector de nuevo a ese tratamiento para mayores detalles.

Observe que, a excepción del potencial químico\(\mu\), todas estas cantidades son propiedades extensas que dependen linealmente del número de moléculas en el sistema\(N\). Excepto por el potencial químico\(\mu\) y la presión\(p\), todas las variables que aparecen en estas expresiones se han definido anteriormente cuando mostramos las expresiones explícitas para las funciones de traslación, vibración, rotación y partición electrónica. Estas son las ecuaciones de trabajo que permiten calcular las propiedades termodinámicas de moléculas estables, iones e incluso especies reactivas como los radicales en términos de propiedades moleculares como geometrías, frecuencias vibracionales, energías y degeneraciones de estado electrónico, y la temperatura, presión y volumen.

Modelos de sólidos de Einstein y Debye

Estos dos modelos tratan de las vibraciones de los cristales que implican movimientos entre los átomos vecinos, iones o moléculas que comprenden el cristal. Estas vibraciones entre fragmentos se llaman fonones. En el modelo de Einstein de un cristal, se supone que:

1. Cada átomo, ion o molécula a partir de la cual se constituye el cristal está atrapado en un potencial bien formado por sus interacciones con especies vecinas. Este potencial se denota\(\phi(V/N)\) con la\(\dfrac{V}{N}\) relación volumen-número escrita para tener en cuenta que probablemente depende de la densidad de empaquetamiento (es decir, las distancias entre vecinos) dentro del cristal. Tenga en cuenta que f representa la interacción de cualquier átomo, ion o molécula específica con la\(N-1\) otra especie de este tipo. Entonces,\(\dfrac{N \phi}{2}\), no\(N \phi\) es la energía total de interacción entre todas las especies; el factor de\(\dfrac{1}{2}\) es necesario para evitar el doble conteo.
2. Se supone que cada especie sufre movimientos vibratorios armónicos locales alrededor de su posición de equilibrio (\(q_J^0\)) dentro del pozo local que la atrapa. Si el cristal es isotrópico, las constantes de fuerza\(k_J\) que caracterizan el potencial armónico\(\dfrac{1}{2} k_J(q_J-q­_J^0)^2\) a lo largo de las\(z\) direcciones\(x\)\(y\), y son iguales; si no, estos\(k_J\) parámetros pueden ser desiguales. Son estas constantes de fuerza, junto con las masas\(m\) de los átomos, iones o moléculas, las que determinan las frecuencias armónicas\(\nu_J = \dfrac{1}{2}\pi \sqrt{\dfrac{k_J}{m}}\) del cristal.
3. Entonces se supone que la función de partición vibracional de fonones entre especies del cristal es un producto de funciones de\(N\) partición, una para cada átomo, ion o molécula en el cristal, con cada función de partición tomada como de la forma vibracional armónica:

\[Q = \exp\bigg(-\dfrac{N \phi}{2kT}\bigg) \left\{\prod_{J=1}^3 \dfrac{\exp(-h\nu_J/2kT)}{1-\exp(-h\nu_J/kT)}\right\}^N.\]

No hay factor de\(N!\) en el denominador porque, a diferencia de un gas de\(N\) especies, cada una de estas\(N\) especies (átomos, iones o moléculas) están obligadas a permanecer puestas (es decir, no libres para vagar independientemente) en la trampa inducida por sus vecinos. En este sentido, las\(N\) especies son distinguibles más que indistinguibles como lo son en el caso del gas. El\(\dfrac{N\phi}{2kT}\) factor surge cuando uno pregunta cuál es la energía total del cristal, aparte de su energía vibratoria, relativa a especies\(N\) separadas; en otras palabras, cuál es la energía cohesiva total del cristal. Esta energía es\(N\) veces la energía de cualquier especie individual\(\phi\), pero, como se señaló anteriormente, dividida por 2 para evitar el doble recuento de las energías de interacción entre especies.

Esta función de partición puede ser sometida a las ecuaciones termodinámicas discutidas anteriormente para calcular diversas propiedades termodinámicas. Una de las más útiles para discutir para los cristales es la capacidad calorífica\(C_V\), la cual viene dada por (ver la contribución vibracional a\(C_V\) expresada en la Sección 7.5.1):

\[C_V = Nk \sum_{J=1,3} \left(\dfrac{h\nu_J}{kT}\right)^2 \dfrac{\exp(h\nu_J/kT) }{(\exp(h\nu_J/kT) –1)^2}.\]

A temperaturas muy altas, se puede demostrar que esta función se aproxima\(3Nk\), lo que concuerda con la observación experimental conocida como la ley de Dulong y Petit. Sin embargo, a temperaturas muy bajas, esta expresión se acerca a:

\[C_V \rightarrow \sum_{J=1,3} Nk \left(\dfrac{h\nu_J}{kT}\right)^2 \exp\Big(-\dfrac{h\nu_J}{kT}\Big),\]

que va a cero a medida que\(T\) se acerca a cero, pero no de una manera que sea consistente con la observación experimental. Es decir, datos experimentales cuidadosos muestran que todas las capacidades de calor de los cristales se acercan\(T^3\) a cero proporcionalmente a baja temperatura; el modelo de Einstein\(C_V\) se acerca a cero pero no en la\(T^3\) forma encontrada en los experimentos.

Entonces, aunque el modelo de Einstein ofrece un modelo muy útil de cómo se relaciona la estabilidad de un cristal\(N\phi\) y cómo\(C_V\) depende de las frecuencias vibracionales de los modos de fonón, no funciona bien a bajas temperaturas. Sin embargo, sigue siendo un modelo ampliamente utilizado en el que entender las contribuciones de los fonones a las propiedades termodinámicas siempre y cuando no se intente extrapolar sus predicciones a bajas\(T\).

En el modelo Debye de fonones en cristales, se abandona la visión en la que cada átomo, ión o molécula vibra independientemente sobre su propia posición de equilibrio y la reemplaza con una visión en la que las especies constituyentes vibran colectivamente en movimientos ondulados. Cada una de esas ondas tiene una longitud de onda\(\lambda\) y una frecuencia\(\nu\) que están relacionadas con la velocidad\(c\) de propagación de tales ondas en el cristal por

\[c = \lambda \nu.\]

La velocidad\(c\) es una característica de las fuerzas entre especies del cristal; es grande para los cristales rígidos y pequeña para los cristales blandos.

De una manera muy parecida a la que usamos para determinar la densidad de estados cuánticos\(\Omega(E)\) dentro de una caja tridimensional, se puede determinar cuántas ondas pueden caber dentro de una caja cristalina cúbica que tiene frecuencias entre\(\nu\) y\(\nu + d\nu\). El enfoque de este problema es expresar las longitudes y frecuencias de onda permitidas como:

\[\lambda_n = \dfrac{2L}{n},\]

\[\nu_n = \dfrac{n c}{2L},\]

donde\(L\) es la longitud de la caja en cada uno de sus lados y\(\nu\) es un entero\(1, 2, 3, \cdots\). Esta prescripción obliga a todas las longitudes de onda a coincidir con la condición de límite para desaparecer en los límites de la caja.

Luego llevar a cabo un recuento de cuántas (\(\Omega(\nu)\)) ondas tienen frecuencias entre\(\nu\) y\(\nu + d\nu\) para una caja cuyos lados son todos iguales da la siguiente expresión:

\[\Omega(\nu) = \dfrac{12\pi V \nu^2}{c^3}.\]

La observación primaria a realizar es que la densidad de las ondas es proporcional a\(\nu^2\):

\[\Omega(\nu) = a \nu^2.\]

Es convencional definir el parámetro a en términos de la frecuencia máxima\(\nu_m\) que se obtiene al requerir que la integral de\(\Omega(\nu)\) sobre todo permitido\(\nu\) sume hasta\(3N\), el número total de vibraciones entre especies que pueden ocurrir:

\[3N = \int \Omega(\nu) d\nu = \dfrac{a \nu_m^3}{3}.\]

Esto da entonces la constante a en términos de\(\nu_m\)\(N\) y y\(\Omega(\nu)\) permite escribirse como

\[\Omega(\nu) = \dfrac{9N}{\nu_m^3}.\]

El modelo de Debye utiliza esta imagen de onda y calcula la energía total\(E\) del cristal tanto como se hace en el modelo de Einstein, pero con la suma sobre los modos\(3N\) vibracionales reemplazada por una integral continua sobre las frecuencias\(\nu\) ponderadas por la densidad de tales estados\(\Omega(\nu)\) (ver contribución vibracional a\(E\) expresada en la Sección 7.5.1):

\[E = \dfrac{N\phi}{2} + \dfrac{9NkT}{\nu_m^3} \int \left[\dfrac{h\nu}{2kT} + \dfrac{h\nu /kT}{\exp(h\nu /kT) –1} \right]\nu^2 d\nu,\]

donde la integral sobre\(\nu\) varía de 0 a nm. Resulta que la capacidad\(C_V\) calorífica obtenida al tomar el derivado de temperatura de esta expresión para se\(E\) puede escribir de la siguiente manera:

\[C_V = 3Nk \left[ 4 D\dfrac{h\nu_m}{kT} – \dfrac{3(h\nu_m/kT)}{\exp(h\nu_m/kT) –1} \right]\]

donde la llamada función Debye\(D(u)\) está definida por

\[D(u) = 3 u^{-3} \int \dfrac{x^3}{\exp(x) – 1} dx,\]

y la integral se toma de\(x = 0\) a\(x = u\).

Lo importante a destacar del modelo Debye es que la capacidad calorífica, como se definió anteriormente, se extrapola a a altas\(3Nk\) temperaturas, coincidiendo así con la ley de Dulong y Petit, y varía a baja temperatura como

\[C_V \rightarrow \dfrac{12}{5} Nk\pi^4 \left(\dfrac{kT}{h\nu_m}\right)^3.\]

Entonces, la capacidad calorífica de Debye sí varía tan\(T^3\) baja\(T\) como indican experimentos cuidadosos. Por esta razón, es apropiado utilizar el modelo Debye siempre que uno esté interesado en tratar adecuadamente la energía, la capacidad calorífica y otras propiedades termodinámicas de los cristales a temperaturas para las cuales\(\dfrac{kT}{h\nu_m}\) es pequeña. A temperaturas más altas, es apropiado usar los modelos Debye o Einstein. La mayor diferencia entre los dos radica en cómo tratan el espectro de frecuencias vibracionales que ocurren en un cristal. El modelo de Einstein dice que solo se produce una frecuencia (o como máximo tres, si se utilizan tres\(k_J\) valores diferentes)\(\nu_J = \dfrac{1}{2}\pi \sqrt{\dfrac{k_J}{m}}\); se supone que cada especie en el cristal vibra a esta frecuencia. En contraste, el modelo de Debye dice que las especies vibran colectivamente y con frecuencias que van desde\(n = 0\) hasta\(\nu = \nu_m\), la llamada frecuencia de Debye, que es proporcional a la velocidad\(c\) a la que los fonones se propagan en el cristal. A su vez, esta velocidad depende de la rigidez (es decir, los potenciales entre especies) dentro del cristal.

Teorías de celosía de superficies y líquidos

Este tipo de teoría se puede aplicar a una amplia variedad de problemas químicos y físicos, por lo que es un modelo muy útil a tener en cuenta. El punto de partida del modelo es considerar una celosía que contiene\(M\) sitios, cada uno de los cuales tiene sitios vecinos\(c\) más cercanos (n.b., claramente,\(c\) dependerá de la estructura de la celosía) e imaginar que cada uno de estos sitios puede existir en cualquiera de los dos estados que etiquetamos A y B. Antes de derivar las ecuaciones básicas de este modelo, permítanme explicar cómo se utilizan los conceptos de sitios y estados A y B para aplicar el modelo a diversos problemas.

1. Los sitios pueden representar sitios de unión en la superficie de un sólido y los dos estados A y B pueden representar situaciones en las que el sitio está ocupado (A) o desocupado (B) por una molécula que se quimiorbe o fisisorbe al sitio. Este punto de vista se toma cuando se aplican modelos de celosía a la adsorción de gases o líquidos a superficies sólidas.
2. Los sitios pueden representar espín individual = 1/2 moléculas o iones dentro de una red, y los estados A y B pueden denotar los estados de espín a y b de estas especies. Este punto de vista permite que los modelos de celosía se apliquen a materiales magnéticos.
3. Los sitios pueden representar posiciones que cualquiera de dos tipos de moléculas A y B podrían ocupar en un líquido o sólido, en cuyo caso A y B se usan para marcar si cada sitio contiene una molécula A o una B. Es así como aplicamos las teorías de celosía a mezclas líquidas.
4. Los sitios pueden representar conformaciones cis y trans en enlaces dentro de un polímero, y A y B pueden usarse para marcar cada enlace como cis o trans. Es así como utilizamos estos modelos para estudiar conformaciones de polímeros.

En la Figura 7.4, muestro una celosía bidimensional que tiene 25 sitios de los cuales 16 están ocupados por especies oscuras (A) y 9 están ocupadas por especies más ligeras (B).

Figura 7.4 Celosía bidimensional que tiene 25 sitios con 16 especies A y 9 B

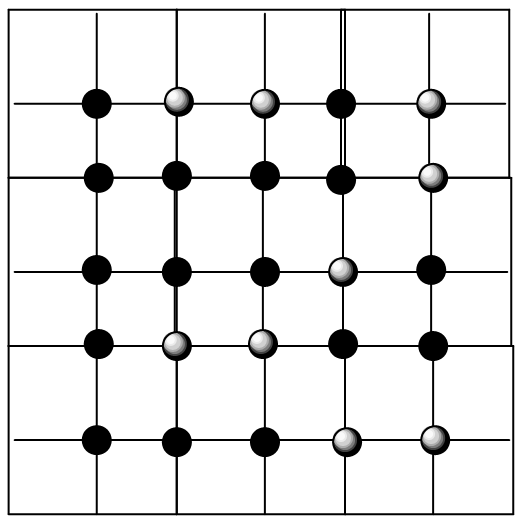
La función de partición para tal celosía se escribe en términos de una degeneración\(\Omega\) y una energía\(E\), como de costumbre. La degeneración se calcula considerando el número de formas en que se puede disponer un total de\(N_A + N_B\) especies en la celosía:

\[\Omega = \dfrac{(N_A+N_B)!}{N_A! N_B!}.\]

Se supone que la energía de interacción entre las especies A y B para cualquier disposición de la A y B en la red se expresa en términos de energías de interacción por pares. En particular, si solo se consideran las energías de interacción del vecino más cercano, se puede escribir la energía\(E­_{\rm ­int}\) de interacción total de cualquier arreglo como

\[E_{\rm int} = N_{AA} E_{AA} + N_{BB} E_{BB} + N_{AB} E_{AB}\]

donde\(N_{IJ}\) es el número de pares vecinos más cercanos de tipo I-J y\(E_{IJ}\) es la energía de interacción de un par I-J. El ejemplo mostrado en la Figura 7.4 tiene\(N_{AA} = 16\),\(N_{BB} = 4\) y\(N_{AB} = 19\).

Los tres parámetros\(N_{IJ}\) que caracterizan tal disposición pueden ser reexpresados en términos de los números\(N_A\) y\(N_B\) de las especies A y B y el número de vecinos más cercanos por sitio de la\(c\) siguiente manera:

\[2N_{AA} + N_{AB} = cN_A\]

\[2N_{BB} + N_{AB} = cN_B.\]

Obsérvese que la suma de estas dos ecuaciones establece el hecho obvio de que el doble de la suma de los pares AA, BB y AB debe ser igual al número de especies A y B multiplicado por el número de vecinos por especie,\(c\).

Usando las relaciones anteriores entre\(N_{AA}\)\(N_{BB}\), y\(N_{AB}\), podemos reescribir la energía de interacción como

\[E_{\rm int} = E_{AA} \dfrac{c N_A – N_{AB}}{2} + E_{BB} \dfrac{c N_B – N_{AB}}{2} + E_{AB} N_{AB}\]

\[=\dfrac{(N_A E_{AA} + N_B E_{BB}) c}{2} + \dfrac{(2 E_{AB} – E_{AA} – E_{BB} ) N_{AB}}{2}\]

La razón por la que es útil escribir\(E_{\rm int}\) de esta manera es que nos permite expresar cosas en términos de dos variables sobre las cuales una tiene control experimental directo\(N_B\),\(N_A\) y, y una variable\(N_{AB}\) que caracteriza el grado de desorden entre las especies A y B. Es decir, si\(N_{AB}\) es pequeña, las especies A y B se disponen en la celosía de manera separada por fases; mientras que, si\(N_{AB}\) es grande, la A y la B están bien mezcladas.

La función de partición total de las especies A y B dispuestas en la celosía se escribe de la siguiente manera:

\[Q = q_A^{N_A} q_B^{N_B} \sum_{N_{AB}} \Omega(N_A, N_B, N_{AB}) \exp(-E_{\rm int}/kT).\]

Aquí,\(q_A\) y\(q_B\) están las funciones de partición (electrónica, vibracional, etc.) de las especies A y B ya que se sientan unidas a un sitio de celosía y\(\Omega(N_A, N_B, N_{AB})\) es el número de formas en que las\(N_A\) especies de tipo A y\(N_B\) de tipo B pueden disponerse en la celosía de tal manera que existen\(N_{AB}\) Vecinos más cercanos tipo A-B. Por supuesto,\(E_{\rm int}\) es la energía de interacción discutida anteriormente. La suma se produce porque una función de partición es una suma sobre todos los estados posibles del sistema. No hay (\(1/N_J!\)) factores porque, como en los modelos de cristal de Einstein y Debye, las especies A y B no son libres de deambular sino que están atadas a sitios de celosía y por lo tanto son distinguibles.

Esta expresión for se\(Q\) puede reescribir de una manera que sea más útil empleando las relaciones anteriores para\(N_{AA}\) y\(N_{BB}\):

\[Q = \Bigl(q_A \exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)^{N_A} \Bigl(q_B\exp\Bigl(-\dfrac{cE_{BB}}{2kT}\Bigr)\Bigr)^{N_B} \sum_{N_{AB}} \Omega(N_A, N_B, N_{AB}) \exp\Bigl(\dfrac{N_{AB}X}{2kT}\Bigr),\]

donde

\[X = (-2 E_{AB} + E_{AA} + E_{BB} ).\]

La cantidad\(X\) juega un papel central en todas las teorías reticulares porque proporciona una medida de cuán diferente es la energía de interacción A-B del promedio de las energías de interacción A-A y B-B. Como veremos pronto, si\(X\) es grande y negativo (es decir, si las interacciones A-A y B-B son altamente atractivas), se puede producir separación de fases; si\(X\) es positiva, no ocurrirá separación de fases.

El problema con la expresión anterior para la función de partición es que nadie ha determinado todavía una expresión analítica para el\(\Omega(N_A, N_B, N_{AB})\) factor de degeneración. Por lo tanto, en la teoría de celosía más elemental, conocida como la aproximación de Bragg-Williams, se aproxima la suma\(N_{AB}\) tomando el siguiente valor promedio de\({AB}\):

\[N_{AB}^* = \dfrac{N_A(cN_B)}{N_A+N_B}\]

en la expresión para\(\Omega\). Este promedio se forma tomando el número de sitios A y multiplicando por el número de sitios vecinos (c) y por la fracción de estos sitios vecinos que serían ocupados por una especie B si la mezcla fuera aleatoria. Esta aproximación produce

\[Q = \Bigl(q_A \exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)^{N_A} \Bigl(q_B\exp\Bigl(-\dfrac{cE_{BB}}{2kT}\Bigr)\Bigr)^{N_B} \exp\Bigl(\dfrac{N_{AB}^*X}{2kT}\Bigr) \sum_{N_{AB}} \Omega(N_A, N_B, N_{AB}).\]

Finalmente, nos damos cuenta de que la suma\(\sum_{N_{AB}} \Omega(N_A, N_B, N_{AB})\) es igual al número de formas de organizar especies\(N_A\) A y especies\(N_B\) B en la celosía independientemente de cuántos pares de vecinos A-B haya. Este número es, por supuesto,\(\dfrac{(N_A+N_B)!}{N_A!N_B!}\).

Entonces, la función de partición del modelo de celosía de Bragg-Williams reduce a:

\[Q = \Bigl(q_A \exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)^{N_A} \Bigl(q_B\exp\Bigl(-\dfrac{cE_{BB}}{2kT}\Bigr)\Bigr)^{N_B} \dfrac{(N_A+N_B)!}{N_A!N_B!} \exp\Bigl(\dfrac{N_{AB}^*X}{2kT}\Bigr).\]

La conexión más común que se hace con las mediciones experimentales que utilizan esta función de partición surge calculando los potenciales químicos de las especies A y B en la red y equiparándolos a los potenciales químicos de la A y B tal como existen en la fase gaseosa. De esta manera, se utilizan las condiciones de equilibrio (potenciales químicos iguales en dos fases) para relacionar las presiones de vapor de A y B, que surgen a través de los potenciales químicos en fase gaseosa, con la energía de interacción\(X\).

Déjame ahora mostrarte cómo se hace esto. Primero, utilizamos

\[\mu_J = -kT \left(\dfrac{∂\ln Q}{∂N_J}\right)_{T,V}\]

para calcular los potenciales químicos A y B en la red. Esto da

\[\mu_A = -kT\left\{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr) – \ln\Bigl(\dfrac{N_A}{N_A+N_B}\Bigr) + \Bigl(1-\dfrac{N_A}{N_A+N_B}\Bigr)^2 \dfrac{cX}{2kT} \right\}\]

y una expresión análoga para\(\mu_B\) con la\(N_B\) sustitución\(N_A\). La expresión para los potenciales químicos en fase gaseosa\(\mu_A^g\) y\(\mu_B^g\) dada anteriormente en este Capítulo tiene la forma:

\[\mu = - kT \ln \left(\left[\dfrac{2\pi mkT}{\hbar^2}\right]^{3/2} \dfrac{kT}{p}\right) – kT \ln\left(\dfrac{\sqrt{\pi}}{\sigma} \sqrt{\dfrac{8\pi 2I_AkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_BkT}{\hbar^2}} \sqrt{\dfrac{8\pi 2I_CkT}{\hbar^2}}\right)\]

\[+kT \sum_{J=1}^{3N-6} \left[\dfrac{h\nu_J}{2kT} + \ln\Big(1-\exp\Big(-\dfrac{h\nu_J}{kT}\Big)\Big)\right] - D_e – kT \ln\omega_e,\]

dentro del cual aparece la presión de vapor. La dependencia de la presión de esta expresión en fase gaseosa se puede factorizar para escribir cada una\(\mu\) como:

\[\mu_A^g = \mu_A^0 + kT \ln(p_A),\]

donde\(p_A\) está la presión de vapor de A (en unidades de atmósfera) y\(\mu_A^0\) denota todos los demás factores en\(\mu_A^g\). Así mismo, los potenciales químicos en fase reticular pueden escribirse como un término que contiene el\(N_A\) y\(N_B\) dependencia y un término que no:

\[\mu_A = -kT\left\{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr) – \ln X_A + (1-X_A)^2 \dfrac{cX}{2kT} \right\},\]

donde\(X_A\) está la fracción molar de A (\(\dfrac{N_A}{N_A+N_B}\)). Por supuesto, una expresión análoga se sostiene para\(\mu_B\).

Ahora realizamos dos pasos:

1. Equiparamos los potenciales químicos en fase gaseosa y en fase reticular de la especie A en un caso en el que la fracción molar de A es la unidad. Esto da\[\mu_A^0 + kT \ln(p_A^0) = -kT{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr)}\] dónde\(p_A^0\) está la presión de vapor de A que existe sobre la celosía en la que solo están presentes las especies A.
2. Equiparamos los potenciales químicos en fase gaseosa y reticular de A para un potencial químico arbitrario\(X_A\) y obtenemos:\[\mu_A^0 + kT \ln(p_A) = -kT\left\{ \ln\Bigl(q_A\exp\Bigl(-\dfrac{cE_{AA}}{2kT}\Bigr)\Bigr) – \ln X_A + (1-X_A)^2 \dfrac{cX}{2kT} \right\},\] que contiene la presión\(p_A\) de vapor de A sobre la red cubierta por A y B con\(X_A\) ser la fracción molar de A.

Restando estas dos ecuaciones y reordenando, obtenemos una expresión de cómo depende la presión de vapor de A de\(X_A\):

\[p_A = p_A^0 X_A \exp\Bigl(-\dfrac{cX(1-X_A)^2}{2kT}\Bigr).\]

Recordemos que la cantidad\(X\) está relacionada con las energías de interacción entre diversas especies como

\[X = (-2 E_{AB} + E_{AA} + E_{BB} ).\]

Examinemos ese significado físico del resultado anterior para la presión de vapor. Primero, si uno ignorara totalmente las energías de interacción (es decir, tomando\(X = 0\)), se obtendría la conocida expresión de la Ley de Raoult para la presión de vapor de una mezcla:

\[p_A = p_A^0 X_A\]

\[p_B = p_B^0 X_B.\]

En la Figura 7.5, se representan las presiones de vapor A y B vs\(X_A\). Las dos líneas rectas son, por supuesto, solo los hallazgos de la Ley de Raoult. También grafico la presión de\(p_A\) vapor para tres valores del parámetro de energía de\(X\) interacción. Cuando\(X\) es positivo, lo que significa que las interacciones A-B son más favorables energéticamente que el promedio de las interacciones A-A y B-B, se encuentra que la presión de vapor de A se desvía negativamente de la predicción de la Ley de Raoult. Esto significa que la presión de vapor observada es inferior a la esperada basada únicamente en la Ley de Raoult. Por otro lado, cuando\(X\) es negativa, la presión de vapor se desvía positivamente de la Ley de Raoult.

Figura 7.5. Gráficas de presiones de vapor en una mezcla A, B como se predijo en el modelo reticular con la aproximación de Bragg-Williams.

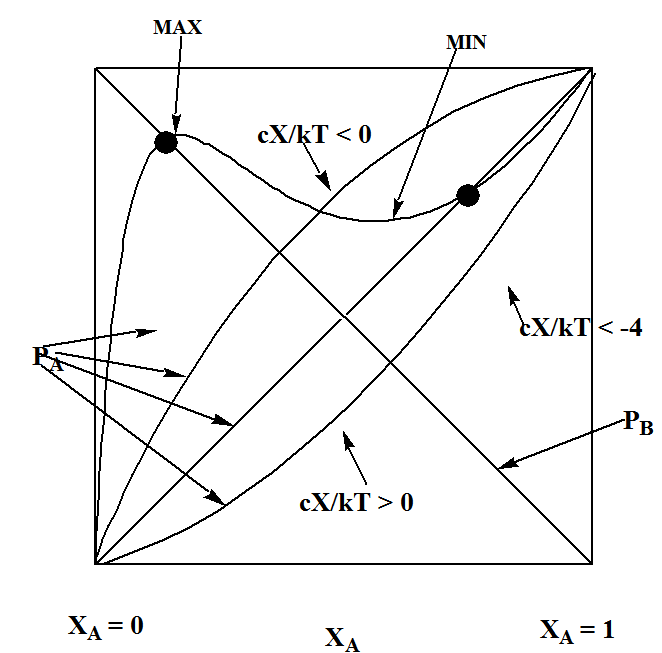
Un caso especialmente importante e interesante surge cuando el\(X\) parámetro es negativo y tiene un valor que hace que\(\dfrac{cX}{2kT}\) sea más negativo que —4. Resulta que en tales casos, la función\(p_A\) sugerida en este modelo de Bragg-Williams muestra un comportamiento que sugiere que puede ocurrir una transición de fase. Los indicios de este comportamiento son claros en la Figura 7.5 donde una de las gráficas muestra tanto un máximo como un mínimo, pero las parcelas para\(X > 0\) y para no\(\dfrac{cX}{2kT} > -4\) lo hacen. Permítanme explicar esto más a fondo examinando la derivada de\(p_A\) con respecto a\(X_A\):

\[\dfrac{dp_A}{dX_A} = p_A^0 \left\{1 + X_A(1-X_A) \dfrac{2cX}{2kT}\right\} \exp\Bigl(-\dfrac{cX(1-X_A)^2}{2kT}\Bigr).\]

Estableciendo esta derivada a cero (en busca de un máximo o mínimo), y resolviendo los valores de\(X_A\) que lo hacen posible, se obtiene:

\[X_A= \dfrac{1 ± \sqrt{1+4kT/cX} }{2}.\]

Debido a que\(X_A\) es una fracción molar, debe ser menor que la unidad y mayor que cero. El resultado anterior da la fracción molar en la que no\(\dfrac{dp_A}{dX_A} = 0\) producirá un valor realista de\(X_A\) a menos que

\[\dfrac{cX}{kT} < - 4.\]

Si\(\dfrac{cX}{kT} = -4\), solo hay un valor de\(X_A\) (es decir,\(X_A\) = 1/2) que produce una pendiente cero; para\(\dfrac{cX}{kT} < -4\), habrá dos de esos valores dados por\(X_A = \dfrac{1 ± \sqrt{1+4kT/cX} }{2}\), que es lo que vemos en la Figura 7.5 donde la gráfica muestra tanto un máximo como un mínimo.

¿Qué significa\(\dfrac{cX}{kT}\) para ser menor que\(-4\) y por qué es esto importante? \(X\)Para ser negativo, significa que el promedio de las interacciones A-A y B-B son más favorables energéticamente que las interacciones A-B. Es por esta razón que se puede favorecer una separación de fases en tales casos (es decir, las especies A prefieren estar cerca de otras especies A más que estar cerca de las especies B, y de manera similar para las especies B). Sin embargo, el movimiento térmico puede superar una ligera preferencia por dicha separación. Es decir, si no\(X\) es lo suficientemente grande,\(kT\) puede superar esta ligera preferencia. Es por ello que\(cX\) debe ser menor que\(-4kT\), no sólo menor que cero.

Entonces, la conclusión es que si las interacciones A-A y B-B son más atractivas, en promedio, que las interacciones A-B, se puede experimentar una separación de fases en la que las especies A y B no permanecen mezcladas en la red sino que se reúnen en dos tipos distintos de dominios. Un dominio será rico en la especie A, teniendo un\(X_A\) valor igual al que se muestra en el punto derecho en la Figura 7.5. Los otros dominios serán ricos en B y tendrán un\(X_A\) valor del que muestra el punto izquierdo.

Como señalé en la introducción a esta Sección, los modelos de celosía se pueden aplicar a una variedad de problemas. Acabamos de analizar cómo se aplica, dentro de la aproximación de Bragg-Williams, a mezclas de dos especies. De esta manera, obtenemos expresiones de cómo las presiones de vapor de las dos especies en la mezcla líquida o sólida muestran un comportamiento que refleja sus energías de interacción. Permítanme ahora mostrarles brevemente cómo se aplica el modelo de celosía en algunas otras áreas.

Al estudiar la adsorción de gases a sitios sobre una superficie sólida, se imagina una superficie que contiene M sitios por unidad de área A con\(N_{ad}\) moléculas (que han sido adsorbidas de la fase gaseosa) unidas a estos sitios. En este caso, la energía de interacción\(E_{\rm int}\) introducida anteriormente implica solo interacciones entre moléculas adsorbidas vecinas; no hay interacciones laterales entre sitios de superficie vacía o entre sitios de superficie vacía y moléculas adsorbidas. Entonces, podemos hacer los siguientes reemplazos en nuestras ecuaciones anteriores:

\[N_A \rightarrow N_{ad}\]

\[N_B \rightarrow M – N_{ad}\]

\[E_{\rm int} = E_{­ad,ad} N_{ad,ad},\]

donde\(N_{ad,ad}\) es el número de pares vecinos más cercanos de especies adsorbidas y\(E_{ad,ad}\) es la energía de interacción por pares entre dicho par. El resultado primario obtenido al equiparar los potenciales químicos de las moléculas en fase gaseosa y adsorbidas es:

\[p = kT \dfrac{q_{gas}}{V} \dfrac{1}{q_{ad}} \dfrac{\theta}{1-\theta} \exp\Big(\dfrac{E_{ad}c\theta}{kT}\Big).\]

Aquí\(q_{gas}/V\) está la función de partición de las moléculas en fase gaseosa por unidad de volumen,\(q_{ad}\) es la función de partición de las moléculas adsorbidas (que contiene la energía de adsorción como\(\exp(-\phi /kT))\) y\(\theta\) se llama la cobertura (es decir, la fracción de sitios superficiales a los que se han adsorbido las moléculas). Claramente,\(\theta\) juega el papel que la fracción molar\(X_A\) jugó antes. Esta denominada ecuación de isoterma de adsorción permite conectar la presión del gas por encima de la superficie sólida a la cobertura.

Como en nuestro ejemplo anterior, algo inusual ocurre cuando la cantidad\(E_{ad}c\theta/kT\) es negativa y más allá de un valor crítico. En particular, diferenciando la expresión para\(p\) con respecto a\(\theta\) y encontrando para qué\(\theta\) valor (s)\(dp/d\theta\) desaparece, se encuentra:

\[q = \dfrac{ 1 ± \sqrt{1 +4kT/cE_{ad}} }{2}.\]

Dado que\(\theta\) es una fracción positiva, esta ecuación solo puede producir valores útiles si

\[\dfrac{cE_{ad}}{kT} < -4.\]

En este caso, esto significa que si las atracciones entre las moléculas adsorbidas vecinas son lo suficientemente fuertes, puede superar factores térmicos para provocar que se produzca la separación de fases. El tipo de separación de fases en los observadores es la formación de islas de moléculas adsorbidas separadas por regiones donde la superficie tiene pocas o ninguna molécula adsorbida.

Hay otra área donde este tipo de modelo de celosía es ampliamente utilizado. Cuando se estudian materiales magnéticos, a menudo se usa el modelo reticular para describir las interacciones entre pares de espines vecinos (por ejemplo, electrones desapareados en moléculas vecinas o espines nucleares en moléculas vecinas). En esta aplicación, se asume que los estados de espín hacia arriba o hacia abajo se distribuyen entre los sitios de celosía, los cuales representan dónde se encuentran las moléculas. \(N_\alpha\)y\(N_\beta\) son el número total de tales giros, por lo que (\(N_\alpha - N_\beta\)) es una medida de lo que se llama la magnetización neta de la muestra. El resultado de aplicar la aproximación de Bragg-Williams en este caso es que se observa nuevamente una condición crítica bajo la cual ocurren fuertes emparejamientos de espín. En particular, debido a que las interacciones entre los giros a y a, denotados\(–J\), y entre\(\alpha\) y los\(\beta\) giros, denotados\(+ J\), son iguales y opuestos, la característica\(X\) variable de todos los modelos de celosía se reduce a:

\[X = -2E_{\alpha,\beta} + E_{\alpha,\alpha} + E_{\beta,\beta} = -4 J.\]

La condición crítica bajo la cual se espera que los giros similares se emparejen y, por lo tanto, formen islas de centros ricos en A y otras islas de centros ricos en b es

\[-\dfrac{4 cJ}{kT} < - 4\]

o

\[\dfrac{cJ}{kT} > 1.\]

Correcciones viriales al comportamiento ideal-gas

Recordemos de nuestro tratamiento anterior de la función de partición clásica que se puede descomponer la función de partición total en un producto de dos factores:

\[Q = \dfrac{h^{-NM}}{N!}\int \exp \Big(- \dfrac{H^0(y, p)}{kT}\Big) dy dp \int \exp \Big(-\dfrac{U(r)}{kT}\Big) dr\]

uno de los cuales

\[Q_{\rm ideal} = \dfrac{h^{-NM}}{N!} \int \exp \Big(- \dfrac{H^0(y, p)}{kT}\Big) dy dp V^N\]

es el resultado si no hay potenciales intermoleculares operativos. El segundo factor

\[Q_{\rm inter} = \dfrac{1}{V^N} {\int \exp \Big(-\dfrac{U(r)}{kT}\Big) dr}\]

por lo tanto, contiene todos los efectos de las interacciones intermoleculares. Recordemos también que todas las ecuaciones que relacionan las funciones de partición con las propiedades termodinámicas implican tomar\(\ln Q\) y derivar de\(\ln Q\). Entonces, todas esas ecuaciones pueden ser echadas en sumas de dos partes; la que surge de\(\ln Q_{\rm ideal}\) y la que surge de\( \ln Q_{\rm inter}\). En esta Sección, estaremos discutiendo las contribuciones de\(Q_{\rm inter}\) a tales ecuaciones.

Lo primero que se hace para desarrollar la llamada expansión de conglomerados de\(Q_{\rm inter}\) es asumir que la energía potencial intermolecular total se puede expresar como una suma de términos aditivos por pares:

\[U = \sum_{I<J} U(r_{IJ})\]

donde\(r_{IJ}\) marca la distancia entre molécula\(I\) y molécula\(J\). Esto permite que el exponencial que aparece en\(Q_{\rm inter}\) sea escrito como un producto de términos, uno por cada par de moléculas:

\[\exp\Big(-\dfrac{U}{kT}\Big) = \exp\Big(- \sum_{I<J} \dfrac{U(r_{IJ})}{kT}\Big) = \prod_{I<J} \exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big).\]

Cada uno de los exponenciales\(\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big)\) se expresa de la siguiente manera:

\[\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big) = 1 + \Big(\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big) –1\Big) = 1 + f_{IJ},\]

siendo la última igualdad lo que define\(f_{IJ}\). Estas\(f_{IJ}\) funciones se introducen porque, cada vez que las moléculas\(I\) y\(J\) están distantes unas de otras y por lo tanto no interactúan, se\(U(r_{IJ})\) desvanece, así\(\exp\Big(- \dfrac{U(r_{IJ})}{kT}\Big)\) se acerca a la unidad, y así se\(f_{IJ}\) desvanece. En contraste, siempre que las moléculas\(I\) y\(J\) estén lo suficientemente cerca como para experimentar fuertes interacciones repulsivas,\(U(r_{IJ})\) es grande y positivo, por lo que\(f_{IJ}\) se acerca\(-1\). Estas propiedades hacen\(f_{IJ}\) una medida útil de cómo interactúan las moléculas; si no lo son\(f = 0\), si están repeliendo fuertemente,\(f = -1\), y si están atrayendo fuertemente,\(f\) es grande y positiva.

Insertando las\(f_{IJ}\) funciones en la expansión del producto del exponencial, se obtiene:

\[\exp\Big(-\dfrac{U}{kT}\Big) = \prod_{I<J} (1 + f_{IJ}) = 1 + \sum_{I<J} f_{IJ} + \sum_{I<J} \sum_{K<L} f_{IJ} f_{KL} + \cdots\]

que se llama la expansión del clúster en términos de las funciones de\(f_{IJ}\) par. Cuando esta expansión se sustituye en la expresión for\(Q_{\rm inter}\), encontramos:

\[Q_{\rm inter} = \dfrac{1}{V^N} \int (1 + \sum_{I<J} f_{IJ} + \sum_{I<J} \sum_{K<L} f_{IJ} f_{KL} + \cdots) dr\]

donde la integral está sobre todas las coordenadas\(3N\) del centro de masa de la\(N\) molécula.

Las integrales que implican una sola\(f_{IJ}\) función son todas iguales (es decir, para cualquier par\(I\)\(J\), las moléculas son idénticas en sus potenciales de interacción) y se reducen a:

\[\dfrac{N(N-1)}{2V^2} \int f(r_1,2) dr_1 dr_2.\]

Las integrales sobre\(dr_3 \cdots dr_N\) producen\(V^{N-2}\), que se combina con\(\dfrac{1}{V^N}\) para producir\(V^{-2}\) lo visto. Finalmente, debido a que\(f(r_{1,2})\) depende únicamente de las posiciones relativas de las moléculas 1 y 2, la integral de seis dimensiones\(dr_1 dr_2\) puede ser reemplazada por integrales sobre la ubicación relativa de las dos moléculas r, y la posición de su centro de masa\(R\). La integral sobre\(R\) da un factor más de\(V\), y la integral de clúster anterior reduce a

\[4\pi \dfrac{N(N-1)}{2V} \int f(r) r^2 dr.\]

con la\(4\pi\) venida de la integral angular sobre la coordenada relativa\(r\). Debido a que el número total de moléculas\(N\) es muy grande, es común escribir el\(\dfrac{N(N-1)}{2}\) factor como\(\dfrac{N^2}{2}\).

También se pueden reducir las integrales del clúster que contienen dos\(f_{IJ} f_{KL}\) factores. Sin embargo, es importante realizar un seguimiento de diferentes tipos de tales factores (dependiendo de si los índices\(I\),\(J\),\(K\),\(L\) son todos diferentes o no). Por ejemplo, términos de la forma

\[\dfrac{1}{V^N} \int f_{IJ} f_{KL} dr_1 dr_2 \cdots dr_N\]

con\(I\),\(J\),\(K\), y\(L\) todo único.

reducir (nuevamente usando la equivalencia de las moléculas y el hecho de que\(f_{IJ}\) depende únicamente de las posiciones relativas de\(I\) y J) a:

\[\dfrac{N^4}{4} (4\pi)^2 V^{-2} \int f_{12} r_{12}^2 dr_{12} \int f_{34} r_{34}^2 dr_{34},\]

donde, de nuevo utilicé el hecho de que\(N\) es muy grande para reemplazarlo\(\dfrac{N(N-1)}{2} \dfrac{(N-2)(N-3)}{2}\) por\(\dfrac{N^4}{4}\).

Por otro lado, las integrales de clúster con, por ejemplo,\( I=K\) pero\(J\) y\(L\) diferentes reducen de la siguiente manera:

\[\dfrac{1}{V^N} \int f_{12} f_{13} dr_1 dr_2 \cdots dr_N = \dfrac{1}{2} V^{-3} N^3 \int f_{12} f_{13} dr_1 dr_2 dr_3.\]

Debido a que\(f_{12}\) depende solo de las posiciones relativas de las moléculas 1 y 2 y\(f_{13}\) depende de las posiciones relativas de 1 y 3, la integral de nueve dimensiones\(dr_1 dr_2 dr_3\) puede cambiarse a una integral de seis dimensiones sobre\(dr_{12} dr_{13}\) y una integral sobre la ubicación de la molécula 1; esta última integral produce un factor de\(V\) cuando se lleva a cabo. Así, la integral del clúster anterior reduce a:

\[(4\pi)^2 \dfrac{1}{2} V^{-2} N^3 \int f_{12} f_{13} r_{12}^2 r_{13}^2 dr_{12} dr_{13} .\]

Existe una diferencia fundamental entre las integrales de clúster del tipo\(f­_{12} f_{34}\) y las que involucran\(f_{12} f_{13}\). Los primeros se denominan clusters no enlazados porque implican la interacción de las moléculas 1 y 2 y una interacción separada de las moléculas 3 y 4. Estos últimos se denominan ligados porque implican la molécula 1 interactuando simultáneamente con las moléculas 2 y 3 (aunque 2 y 3 no necesitan estar lo suficientemente cerca como\(f_{23}\) para provocar que no sean cero). Las principales diferencias entre las contribuciones de cluster no vinculadas y vinculadas son:

1. El número total de términos no vinculados es proporcional a\(N^4\), mientras que el número de términos vinculados es proporcional a\(N^3\). Esto hace que los primeros sean más importantes que los segundos porque son más numerosos.
2. Los términos vinculados solo adquieren importancia en densidades donde existe una probabilidad significativa de que tres moléculas ocupen regiones cercanas del espacio. Los términos no enlazados, por otro lado, no requieren que las moléculas 1 y 2 estén cerca de las moléculas 3 y 4. Esto también hace que los términos no vinculados dominen especialmente a densidades bajas y moderadas.

Debo señalar que una observación similar se hizo en el Capítulo 6 cuando discutimos la interacción de configuración y la expansión de racimo acoplado de las funciones de onda electrónica. Es decir, notamos que las configuraciones doblemente excitadas (análogas a\(f_{IJ}\)) son las contribuciones más importantes más allá del determinante único, y que las excitaciones cuádruples en forma de productos desvinculados de excitaciones dobles fueron las siguientes más importantes, no las excitaciones triples. La naturaleza no ligada en este caso se relacionó con las amplitudes de las excitaciones cuádruples siendo productos de las amplitudes de dos excitaciones dobles. Entonces, tanto en las estructuras electrónicas como en la estructura líquida, se encuentra que las correlaciones de pares seguidas de correlaciones de pares no enlazadas son las más importantes a considerar.

Claramente, el enfoque de expansión de clústeres\(Q_{\rm inter}\) puede llevarse a clústeres de nivel superior y superior (por ejemplo, involucrando\(f_{12} f_{34} f_{56}\) o\(f_{12} f_{13} f_{34}\), etc.). Generalmente, se encuentra que los términos no vinculados (por ejemplo,\(f_{12} f_{34} f_{56}\) en este ejemplo) son los más importantes (porque son proporcionales a potencias superiores de\(N\) y porque no requieren más que colisiones binarias). Es más común, sin embargo, emplear una expansión severamente truncada y retener solo los términos vinculados. Hacerlo para\(Q_{\rm inter}\) produce en los niveles inferiores:

\[Q_{\rm inter} = 1 + \dfrac{1}{2} \Big(\dfrac{N}{V}\Big)^2 4\pi V \int f r^2 dr + \dfrac{1}{4} \Big(\dfrac{N}{V}\Big)^4 [4\pi V \int f r^2 dr ]^2\]

\[+ \dfrac{1}{2} \Big(\dfrac{N}{V}\Big)^3 V (4\pi)^2 \int f_{12} f_{13} r_{12}^2 r_{13}^2 dr_{12} dr_{13}.\]

Una de las propiedades más comunes para calcular usando una función de partición que incluye interacciones moleculares en forma de conglomerado es la presión, que se calcula como:

\[p = kT \left(\dfrac{∂\ln Q}{∂V}\right)_{N,T}.\]

El uso\(Q = Q_{\rm ideal} Q_{\rm inter}\) e inserción de la expresión anterior para\(Q_{\rm inter}\) produce el siguiente resultado para la presión:

\[\dfrac{pV}{NkT} = 1 + B_2 \Big(\dfrac{N}{V}\Big) + B_3 \Big(\dfrac{N}{V}\Big)^2 + \cdots\]

donde los denominados coeficientes viriales\(B_2\) y\(B_3\) se definen como los factores proporcionales a\(\Big(\dfrac{N}{V}\Big)\) y\(\Big(\dfrac{N}{V}\Big)^2\), respectivamente. La expresión del segundo coeficiente virial en términos de las integrales del clúster es:

\[B_2 = - 2\pi \int f r^2 dr = - 2\pi \int \Big[\exp\Big(-\dfrac{U(r)}{kT}\Big) –1\Big] r^2 dr.\]

El tercer coeficiente virial involucra integrales de conglomerado de orden superior.

La importancia de dicho análisis de conglomerados es que permiten que diversas propiedades termodinámicas (por ejemplo, la presión anterior) se expresen como una contribución que ocurriría si el sistema consistiera en moléculas no interactuantes y una segunda contribución que surge de las fuerzas intermoleculares. Por lo tanto, permite mediciones experimentales de la desviación del comportamiento ideal (es decir, no interactuando) para proporcionar una manera directa de determinar potenciales intermoleculares. Por ejemplo, al medir presiones a diversos\(N/V\) valores y diversas temperaturas, se puede determinar\(B_2\) y así obtener información valiosa sobre el potencial intermolecular\(U\).

Colaboradores y Atribuciones

Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry

Integrated by Tomoyuki Hayashi (UC Davis)