7.2: Elasticidad entrópica
- Page ID
- 71902
Modelo de Cadena Ideal
La mayoría de las cadenas poliméricas tienen enlaces giratorios así como ángulos de unión a lo largo de la cadena principal polimérica que difieren de 180\(^\circ\) Esto conduce a la flexibilidad de la cadena. Incluso si las rotaciones no son libres, sino que dan lugar solo a estados\(n_\mathrm{rot}\) rotaméricos por enlace giratorio, el número de posibles conformaciones de cadena se vuelve vasto. Para enlaces\(N_{rot}\) giratorios, el número de conformaciones distintas es\(n_\mathrm{rot}^{N_\mathrm{rot}}\). El modelo útil más simple para una cadena tan flexible es el modelo de cadena articulada libremente. Aquí asumimos vectores de enlace que todos tienen la misma longitud\(l = |\vec{r}_i|\), donde\(\vec{r}_i\) está el vector de\(i^\mathrm{th}\) enlace del enlace. Si además asumimos un ángulo\(\theta_{ij}\) entre vectores de enlace consecutivos, podemos escribir el producto escalar de vectores de enlace consecutivos como
\[\vec{r}_i \cdot \vec{r}_j = l^2 \cos \theta_{ij} \ . \label{eq:fjc_cons}\]
Este producto escalar es de interés, ya que podemos usarlo para calcular la distancia media-cuadrada de extremo a extremo\(\langle R^2 \rangle\) de un conjunto de cadenas, que es el parámetro más simple que caracteriza la dimensión espacial de la cadena. Con el vector de distancia de extremo a extremo de una cadena con\(n\) enlaces,
\[\vec{R}_n = \sum_{i=1}^n \vec{r}_i \ ,\]
tenemos
\[\begin{align} \langle R^2 \rangle & = \langle \vec{R}_n^2 \rangle \\ & = \langle \vec{R}_n \cdot \vec{R}_n \rangle \\ & = \left\langle \left( \sum_{i=1}^n \vec{r}_i \right) \cdot \left( \sum_{j=1}^n \vec{r}_j \right) \right\rangle \\ & = \sum_{i=1}^n \sum_{j=1}^n \langle \vec{r}_i \cdot \vec{r}_j \rangle \ .\end{align}\]
Al usar la ecuación\ ref {eq:fjc_cons}) encontramos
\[\langle R^2 \rangle = l^2 \sum_{i=1}^n \sum_{j=1}^n \langle \cos \theta_{ij} \rangle \ . \label{eq:fjc_double_sum}\]
En el modelo de cadena libremente articulada asumimos además que no hay correlaciones entre las direcciones de diferentes vectores de enlace,\(\langle \cos \theta_{ij} \rangle = 0\) para\(i \neq j\). Entonces, la suma doble en la Ecuación\ ref {eq:fjc_double_sum}) solo tiene términos\(n\) distintos de cero para\(i=j\) con\(\cos \theta_{ij} = 1\). Por lo tanto,
\[\langle R^2 \rangle = n l^2 \ . \label{eq:eer_fjc}\]
Esto nuevamente parece ser un modelo crudo, pero ahora lo rescataremos redefiniendo\(l\). En una cadena de polímero ideal podemos al menos suponer que no hay interacción entre monómeros que están separados por muchos otros monómeros,
\[\lim\limits_{|i-j| \rightarrow \infty} \langle \cos \theta_{ij} \rangle = 0 \ .\]
Además, para un vector de enlace dado\(\vec{r}_i\) la suma de todas las correlaciones con otros vectores de enlace converge a algún número finito que depende de\(i\),
\[\sum_{j=1}^n \langle \cos \theta_{ij} \rangle = C'(i) \ .\]
Por lo tanto, al incluir las correlaciones, la ecuación\ ref {eq:fjc_double_sum}) aún puede simplificarse a
\[\langle R^2 \rangle = l^2 \sum_{i=1}^n C'(i) = C_n n l^2 \ ,\]
donde la relación característica de Flory\(C_n\) es el valor promedio de\(C'(i)\) sobre todos los enlaces de la columna vertebral de la cadena.
En general,\(C_n\) depende de\(n\), pero para cadenas muy largas converge a un valor\(C_\infty\). Para cadenas suficientemente largas, podemos aproximarnos
\[\langle R^2 \rangle \approx n C_\infty l^2 \ ,\]
que tiene la misma dependencia de\(n\) y\(l\) que el modelo crudo de la cadena libremente articulada, Ecuación\ ref {eq:eer_fjc}). Por lo tanto, podemos definir una cadena equivalente libremente articulada con segmentos\(N\) Kuhn de longitud\(b\). Desde
\[\langle R^2 \rangle = N b^2 \approx n C_\infty l^2 \label{eq:Kuhn_R2}\]
y la longitud de la cadena equivalente estirada al máximo, la longitud del contorno\(R_\mathrm{max}\),
\[R_\mathrm{max} = N b \ ,\]
obtenemos
\[N = \frac{R_\mathrm{max}^2}{C_\infty n l^2}\]
y la longitud de Kuhn
\[b = \frac{\langle R^2 \rangle}{R_\mathrm{max}} = \frac{C_\infty n l^2}{R_\mathrm{max}} \ .\]
Los valores típicos de\(C_\infty\) para polímeros sintéticos varían de 4.6 para 1,4-poli (isopreno) a 9.5 para poli (estireno) atáctico con longitudes de Kuhn correspondientes de 8.2 Å a 18 Å, respectivamente.
En este punto hemos encontrado la distancia media cuadrada de extremo a extremo como parámetro de un macroestado de equilibrio. Si estiramos la cadena a una distancia de extremo a extremo más larga, ya no está en equilibrio y debe tener mayor energía libre. Parte de este aumento en la energía libre debe provenir de una disminución en la entropía que el estiramiento induce al reducir el número de conformaciones de cadena accesibles. Resulta que esta contribución entrópica es la mayor parte del incremento de la energía libre, típicamente 90%. La tendencia de las cadenas poliméricas a contraerse después de haber sido estiradas es, por lo tanto, principalmente un efecto entrópico. Para cuantificarlo, necesitamos una distribución de probabilidad para los vectores de extremo a extremo y para ello, introducimos un concepto que es ampliamente utilizado en ciencias naturales.
Caminata Aleatoria
El modelo de cadena articulada libremente asume explícitamente que la dirección del siguiente segmento de Kuhn no está correlacionada con las direcciones de todos los segmentos anteriores de Kuhn. Donde se ubicará el extremo de la cadena después del siguiente paso que prolonga la cadena en un segmento depende únicamente de la ubicación del extremo de la cadena actual. Por lo tanto, la cadena libremente articulada tiene aspectos de una cadena de Markov. Cada paso de prolongación es un evento aleatorio y la trayectoria de la cadena en el espacio una caminata aleatoria.
Muchos procesos pueden ser discretizados en pasos individuales. Lo que ocurra en el siguiente paso puede depender únicamente del estado actual o también de lo que ocurrió en pasos anteriores. Si solo depende del estado actual, el proceso no tiene memoria y se ajusta a la definición de una cadena de Markov. Una cadena de Markov donde los eventos son pasos análogos en algún espacio de parámetros se puede modelar como una caminata aleatoria. Una caminata aleatoria es una sucesión matemáticamente formalizada de pasos aleatorios. Un paseo aleatorio sobre una celosía, donde cada paso solo puede conducir de un punto de celosía a un punto de celosía directamente vecino es un modelo particularmente simple. [concepto:random_walk]
Podemos utilizar el concepto de caminata aleatoria en combinación con los conceptos de termodinámica estadística para resolver el problema del estiramiento y contracción de la cadena polimérica. El problema se resuelve si conocemos la dependencia de la energía libre de Helmholtz en la longitud del vector de extremo a extremo. Esto, a su vez, requiere que conozcamos la entropía y así la distribución de probabilidad de la longitud del vector de extremo a extremo. Esta distribución de probabilidad viene dada por el número de posibles caminatas aleatorias (trayectorias) que conducen a una distancia particular de extremo a extremo\(\sqrt{\vec{R}^2}\).
Por simplicidad partimos de un ejemplo más sencillo en una dimensión que posteriormente podremos extender a tres dimensiones. Consideramos el ejemplo estándar en este campo, un borracho que acaba de salir de un pub. Suponemos que, a partir de la puerta del pub, da pasos aleatorios adelante y atrás por el camino. ¿Cuál es la probabilidad de\(P(N,x)\) que después de\(N\) escalones esté a una distancia de\(x\) escalones por la carretera desde la puerta del pub? El problema es equivalente a encontrar el número\(W(N,x)\) de trayectorias de longitud\(N\) que terminan\(x\) escalones desde la puerta del pub y dividirla por el número total de trayectorias.
Cualquier trayectoria de este tipo consiste en\(N_+\) escalones por el camino y\(N_-\) escalones por el camino, siendo la posición final\(x = N_+ - N_-\). El número de tales trayectorias viene, nuevamente, dado por una distribución binomial (ver Sección [distribución_binomial_])
\[W(N,x) = \frac{\left( N_+ + N_-\right)!}{N_+! N_-!} = \frac{N!}{\left[ \left(N+x\right)/2\right] ! \left[ \left(N-x\right)/2\right] !} \ ,\]
mientras que el número total de trayectorias es\(2^N\), ya que el borracho tiene dos posibilidades en cada paso. Por lo tanto,
\[P(N,x) = \frac{1}{2^N} \cdot \frac{N!}{\left[ \left(N+x\right)/2\right] ! \left[ \left(N-x\right)/2\right] !} \ ,\]
lo que lleva a
\[\ln P(N,x) = -N \ln 2 + \ln(N!) - \ln \left(\frac{N+x}{2}\right)! - \ln \left(\frac{N-x}{2}\right)! \ .\]
Los dos últimos términos del lado derecho se pueden reescribir como
\[\begin{align} \ln \left(\frac{N + x}{2}\right)! = \ln \left(\frac{N}{2}\right)! + \sum_{s=1}^{x/2} \ln \left( \frac{N}{2} + s \right) \ \textrm{and} \\ \ln \left(\frac{N - x}{2}\right)! = \ln \left(\frac{N}{2}\right)! - \sum_{s=1}^{x/2} \ln \left( \frac{N}{2} + 1 - s \right) \ ,\end{align}\]
lo que lleva a
\[\ln P(N,x) = -N \ln 2 + \ln(N!) - 2\ln \left(\frac{N}{2}\right)! - \sum_{s=1}^{x/2} \ln \left( \frac{N/2 + s}{N/2 + 1 - s} \right) \ . \label{eq:P_N_X_0}\]
Ahora asumimos una larga trayectoria. En el rango donde\(x \ll N\), que se realiza en una fracción abrumadora de todas las trayectorias, los logaritmos del numerador y denominador en el último término en el lado derecho de la Ecuación\ ref {EQ:P_N_x_0}) pueden aproximarse por expansión en serie,\(\ln(1+y) \approx y\) para\(|y| \ll 1\), lo que da
\[\begin{align} \ln \left( \frac{N/2 + s}{N/2 + 1 -s} \right) & = \ln \left( \frac{1 + 2s/N}{1 -2s/N + 2/N} \right) \\ & = \ln \left( 1 + \frac{2s}{N} \right) - \ln\left( 1 - \frac{2s}{N} + 2/N \right) \\ & \approx \frac{4s}{N} - \frac{2}{N} \ . \label{eq:Gauss_approx_0}\end{align}\]
Por lo tanto,
\[\begin{align} \sum_{s=1}^{x/2} \ln \left( \frac{N/2 + s}{N/2 + 1 - s} \right) & = \sum_{s=1}^{x/2} \left( \frac{4s}{N} - \frac{2}{N} \right) \\ & = \frac{4}{N} \sum_{s=1}^{x/2} s - \frac{2}{N} \sum_{s=1}^{x/2} 1 \\ & = \frac{4}{N} \cdot \frac{(x/2)(x/2+1)}{2} - \frac{x}{N} \\ & = \frac{x^2}{2N} \ . \label{eq:Gauss_approx}\end{align}\]
Insertar la ecuación\ ref {EQ:Gauss_approx} en la ecuación\ ref {EQ:P_N_x_0}) proporciona,
\[P(N,x) \approx \frac{1}{2^N} \cdot \frac{N!}{(N/2)!(N/2)!} \cdot \exp\left( - \frac{x^2}{2N} \right) \ ,\]
donde reconocemos, en el último factor del lado derecho, la aproximación de la distribución binomial por una distribución gaussiana que discutimos en la Sección [binomial_distribution]. Usando la fórmula mejorada de Stirling, Ecuación\ ref {EQ:Stirling_Better}), para expresar los factoriales, tenemos
\[\frac{1}{2^N} \cdot \frac{N!}{(N/2)!(N/2)!} = \frac{1}{2^N} \frac{\sqrt{2 \pi N} N^N \exp(-N)}{\left(\sqrt{\pi N} (N/2)^{N/2} \exp(-N/2)\right)^2} = \sqrt{\frac{2}{\pi N}} \ ,\]
lo que lleva al resultado extremadamente simple:
\[P(N,x) = \sqrt{\frac{2}{\pi N}} \exp\left( - \frac{x^2}{2N} \right) \ .\]
El borracho, si se le da suficiente tiempo y no se duerme, simula perfectamente una distribución gaussiana.
Incluso podemos simplificar aún más este resultado preguntando por el desplazamiento cuadrático medio\(\langle x^2 \rangle\), que viene dado por
\[\langle x^2 \rangle = \int_{-\infty}^{\infty} x^2 P(N,x) \mathrm{d}x = \sqrt{\frac{2}{\pi N}} \int_{-\infty}^{\infty} x^2 \exp\left( - \frac{x^2}{2N} \right) \mathrm{d}x = N \ .\]
Antes de continuar, necesitamos solucionar un problema que ocurre cuando interpretamos las probabilidades discretas calculadas en este punto como una distribución continua de densidad de probabilidad de\(x\). En el caso discreto,\(W(N,x)\) puede ser distinto de cero solo para par o impar\(x\), dependiendo de si\(N\) es par o impar. Así, para llegar a la distribución de probabilidad adecuada necesitamos dividirnos por 2. Por lo tanto, podemos expresar la distribución de densidad de probabilidad para una caminata aleatoria unidimensional como
\[\rho_\mathrm{1d}(x) = \frac{1}{\sqrt{2\pi \langle x^2 \rangle}} \exp\left( - \frac{x^2}{2\langle x^2 \rangle} \right) \ .\]
Este resultado ya no depende del tamaño del paso, ni siquiera implícitamente, porque hemos eliminado la dependencia del número de paso\(N\). Por lo tanto, se puede generalizar a tres dimensiones. Dado que los paseos aleatorios a lo largo de las tres direcciones ortogonales por pares en el espacio cartesiano son independientes entre sí, tenemos
\[\rho_\mathrm{3d}(x,y,z) \mathrm{d}x \mathrm{d} y \mathrm{dz} = \rho_\mathrm{1d}(x) \mathrm{d}x \cdot \rho_\mathrm{1d}(y) \mathrm{d}y \cdot \rho_\mathrm{1d}(z) \mathrm{d}z \ .\]
En este punto relacionamos el resultado con el conjunto conformacional de una cadena polimérica ideal, utilizando el modelo de Kuhn discutido en la Sección [subsección:ideal_chain]. Se plantea la cuestión de la distribución de las distancias medio-cuadradas de extremo a extremo\(\left\langle \vec{R}^2 \right\rangle\) con los componentes cartesianos del vector de extremo a extremo\(\vec{R}\) siendo\(x = R_x\),\(y = R_y\), y\(z = R_z\). De acuerdo con la Ecuación\ ref {EQ:KUHN_R2}), tenemos
\[\begin{align} \left\langle \vec{R}^2 \right\rangle & = \left\langle R_x^2 \right\rangle + \left\langle R_y^2 \right\rangle + \left\langle R_z^2 \right\rangle \label{eq:R2_xyz} \\ & = N b^2 \ .\end{align}\]
Por razones de simetría tenemos,
\[\left\langle R_x^2 \right\rangle = \left\langle R_y^2 \right\rangle = \left\langle R_z^2 \right\rangle = \frac{N b^2}{3} \ ,\]
lo que lleva a
\[\rho_\mathrm{1d}(N,x) = \sqrt{\frac{3}{2 \pi N b^2}} \exp \left( -\frac{3R_x^2}{2N b^2} \right)\]
y expresiones análogas para\(\rho_\mathrm{1d}(y)\) y\(\rho_\mathrm{1d}(z)\). Hemos reintroducido el parámetro\(N\), que ahora es el número de segmentos de Kuhn. Sin embargo, al discutir una distribución continua de densidad de probabilidad, hemos eliminado la dependencia de un modelo de celosía. Esto es necesario ya que los pasos a lo largo de las dimensiones\(x\)\(y\),, y\(z\) difieren para cada segmento de Kuhn. Al usar la ecuación\ ref {EQ:R2_XYZ}), encontramos
\[\rho_\mathrm{3d}(N,\vec{R}) = \left( \frac{3}{2 \pi N b^2} \right)^{3/2} \exp \left(-\frac{3 \vec{R}^2}{2 N b^2} \right) \ . \label{eq:rho3d_chain}\]
La densidad de probabilidad alcanza un máximo a cero vector de extremo a extremo.
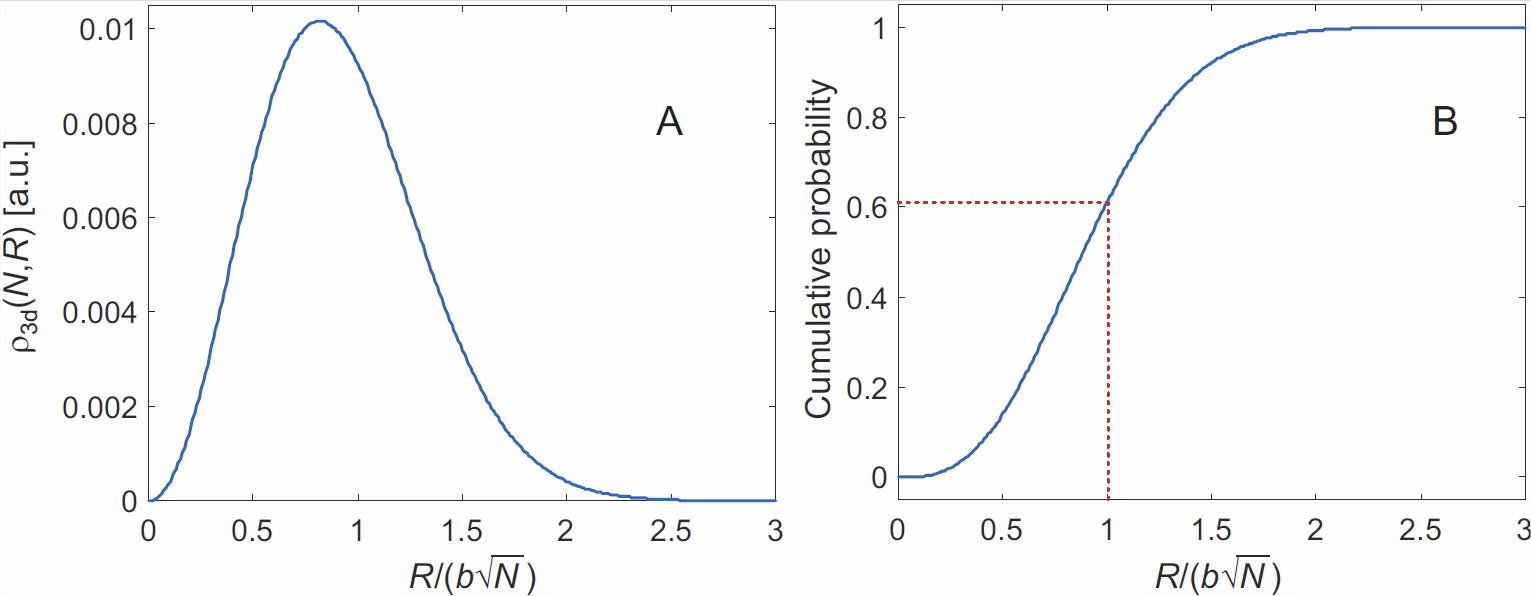
Por último, podemos plantear la siguiente pregunta: Si dejamos que todas las cadenas del conjunto comiencen en el mismo punto, ¿cómo se distribuyen los extremos de la cadena en el espacio? Esto se representa mejor en un sistema de coordenadas esféricas. La simetría dicta que la distribución es uniforme con respecto a los ángulos polares\(\theta\) y\(\phi\). La coordenada polar\(R\) es equivalente a la distancia de extremo a extremo de la cadena. Para encontrar la distribución de probabilidad para esta distancia de extremo a extremo necesitamos incluir el área\(4\pi R^2\) de las conchas esféricas. Por lo tanto,
\[\rho_\mathrm{3d}(N,R) \cdot 4 \pi R^2 \mathrm{d} R = 4 \pi \left( \frac{3}{2 \pi N b^2} \right)^{3/2} \exp \left(-\frac{3 R^2}{2 N b^2} \right) R^2 \mathrm{d} R \ .\]
Debido a esta escala con el volumen de una concha esférica infinitesimalmente delgada, la distribución de densidad de probabilidad (Figura\(\PageIndex{1A}\)) para la distancia de extremo a extremo no alcanza un pico a distancia cero. Como se ve en la Figura\(\PageIndex{1B}\) es muy poco probable que se encuentre con una cadena\(R > 2b\sqrt{N}\). Dado que la longitud del contorno es\(R_\mathrm{max} = Nb\), podemos concluir que en equilibrio casi todas las cadenas tienen distancias de extremo a extremo más cortas que\(2 R_\mathrm{max} / \sqrt{N}\).
Necesitamos discutir la validez del resultado, ya que al aproximar la distribución binomial discreta por una distribución de probabilidad gaussiana continua habíamos hecho la suposición\(x \ll N\). Dentro del modelo de cadena ideal, esta suposición corresponde a una distancia de extremo a extremo que es mucho más corta que la longitud del contorno\(N b\). Si\(R\) se aproxima\(Nb\), la distribución gaussiana sobreestima la densidad de probabilidad verdadera. De hecho, la distribución gaussiana predice una probabilidad pequeña, pero finita, de que la cadena sea más larga que su longitud de contorno, que no es física. El modelo se puede refinar para incluir casos de estiramiento tan fuerte de la cadena. Para nuestra discusión cualitativa de la elasticidad entrópica no muy lejos del equilibrio, podemos contentarnos con la Ecuación\ ref {eq:rho3d_chain}).
Entropía conformacional y energía libre
Ahora podemos plantearnos la cuestión de la dependencia de la energía libre de la extensión de la cadena\(\vec{R}\). Con la definición de entropía de Boltzmann, Ecuación\ ref {eq:Boltzmann_entropía}), y la identificación habitual\(k = k_\mathrm{B}\) tenemos
\[S(N,\vec{R}) = k_\mathrm{B} \ln \Omega(N,\vec{R}) \ .\]
La distribución de densidad de probabilidad en la Ecuación\ ref {eq:rho3d_chain}) está relacionada con el peso estadístico\(\Omega\) por
\[\rho_\mathrm{3d}(N,\vec{R}) = \frac{\Omega(N,\vec{R})}{\int \Omega(N,\vec{R}) \mathrm{d} \vec{R}} \ ,\]
porque\(\rho_\mathrm{3d}\) es la fracción de todas las conformaciones que tienen un vector de extremo a extremo en el intervalo infinitesimalmente pequeño entre\(\vec{R}\) y\(\vec{R} + \mathrm{d}\vec{R}\). De ahí que 22
\[\begin{align} S(N,\vec{R}) & = k_\mathrm{B} \ln \rho_\mathrm{3d}(N,\vec{R}) + k_\mathrm{B} \ln \left[ \int \Omega(N,\vec{R}) \mathrm{d} \vec{R} \right] \\ & = -\frac{3}{2} k_\mathrm{B} \frac{\vec{R}^2}{N b^2} + \frac{3}{2} k_\mathrm{B} \ln \left( \frac{3}{2 \pi N b^2} \right) + k_\mathrm{B} \ln \left[ \int \Omega(N,\vec{R}) \mathrm{d} \vec{R} \right] \ . \label{eq:s_N_R_ideal_chain}\end{align}\]
Los dos últimos términos no dependen\(\vec{R}\) y por lo tanto constituyen una contribución de entropía\(S(N,0)\) que es la misma para todas las distancias de extremo a extremo, sino que depende del número de monómeros\(N\),
\[S(N,\vec{R}) = -\frac{3}{2} k_\mathrm{B} \frac{\vec{R}^2}{N b^2} + S(N,0) \ .\]
Dado que por definición los segmentos Kuhn de una cadena ideal no interactúan entre sí, la energía interna es independiente de\(\vec{R}\). La energía libre de Helmholtz\(F(N,\vec{R}) = U(N,\vec{R}) - T S(N,\vec{R})\) puede escribirse así como
\[F(N,\vec{R}) = \frac{3}{2} k_\mathrm{B} T \frac{\vec{R}^2}{N b^2} + F(N,0) \ .\]
De ello se deduce que la energía libre de una cadena individual alcanza un mínimo a cero vector de extremo a extremo, de acuerdo con nuestra conclusión en la Sección [subsección:random_walk] de que la densidad de probabilidad es máxima para un vector cero de extremo a extremo. En vectores de extremo a extremo más largos, la entropía de cadena disminuye cuadráticamente con la longitud del vector De ahí que la cadena pueda considerarse como un resorte entrópico. El alargamiento del resorte corresponde a separar los extremos de la cadena por una distancia\(R \ll N b\). La fuerza requerida para este alargamiento es la derivada de la energía libre de Helmholtz con respecto a la distancia. Para una dimensión, obtenemos
\[f_x = -\frac{\partial F\left( N, \vec{R} \right)}{\partial R_x} = -\frac{3 k_\mathrm{B} T}{N b^2} \cdot R_x \ .\]
Para el caso tridimensional, la fuerza es un vector que es lineal en\(\vec{R}\),
\[\vec{f} = -\frac{3 k_\mathrm{B} T}{N b^2} \cdot \vec{R} \ ,\]
es decir, el resorte entrópico satisface la ley de Hooke. La constante de resorte entrópica es\(3 k_\mathrm{B} T/(Nb^2)\).
Por lo tanto, los polímeros son más fáciles de estirar cuanto mayor es su grado de polimerización (proporcional a\(N\)), más largo es el segmento de Kuhn\(b\) y menor es la temperatura\(T\). En particular, la dependencia de la temperatura es contraintuitiva. Una cadena de polímero bajo tensión se contraerá si se eleva la temperatura, ya que la contribución entrópica a la energía libre de Helmholtz, que contrarresta la tensión, luego aumenta.