24.2: Termodinámica de Mezcla

Cuando se combinan sólidos, líquidos o gases, las cantidades termodinámicas del sistema experimentan un cambio como resultado de la mezcla. Este módulo discutirá el efecto que la mezcla tiene en la energía Gibbs, entalpía y entropía de una solución, con un enfoque específico en la mezcla de dos gases.

Introducción

Se crea una solución cuando dos o más componentes se mezclan homogéneamente para formar una sola fase. Estudiar soluciones es importante porque la mayoría de los procesos de vida química y biológica ocurren en sistemas con múltiples componentes. Comprender el comportamiento termodinámico de las mezclas es parte integral del estudio de cualquier sistema que involucre soluciones ideales o no ideales, ya que proporciona información valiosa sobre las propiedades moleculares del sistema.

La mayoría de los gases reales se comportan como gases ideales a temperatura y presión estándar. Esto nos permite combinar nuestro conocimiento de los sistemas y soluciones ideales con la termodinámica de estado estándar para derivar un conjunto de ecuaciones que describen cuantitativamente el efecto que la mezcla tiene sobre las cantidades termodinámicas de una solución en fase gaseosa dada.

Gibbs Energía Libre de Mezcla

A diferencia de las extensas propiedades de un sistema de un componente, que dependen únicamente de la cantidad del sistema presente, las propiedades extensas de una solución dependen de su temperatura, presión y composición. Esto significa que una mezcla debe describirse en términos de las cantidades molares parciales de sus componentes. La energía libre total de Gibbs de una solución de dos componentes viene dada por la expresión

\[ G=n_A\overline{G}_A+n_B\overline{G} _B \label{1}\]

donde

• \(G\)es la energía Gibbs total del sistema,
• \(n_i\)es el número de moles de componente\(i\), y
• \(\overline{G}_i\)es la energía molar parcial de Gibbs del componente\(i\).

La energía molar de Gibbs de un gas ideal se puede encontrar usando la ecuación

\[\overline{G}=\overline{G}^\circ+RT\ln \frac{P}{1\text{ bar}} \label{2}\]

donde\( \overline{G}^\circ\) es la energía molar estándar de Gibbs del gas a 1 bar, y P es la presión del sistema. En una mezcla de gases ideales, encontramos que la energía molar parcial de Gibbs del sistema es equivalente a su potencial químico, o que

\[ \overline{G}_i=\mu_i \label{3} \]

Esto significa que para una solución de gases ideales, la ecuación\(\ref{2}\) puede llegar a ser

\[\overline{G}_i=\mu_i=\mu^\circ_i+RT \ln \frac{P_i}{1\text{ bar}} \label{4}\]

donde

• \(\mu_i\)es el potencial químico del componente\(i\) th,
• \(\mu_i^\circ\)es el potencial químico estándar del componente\(i\) a 1 bar, y
• \(P_i\)es la presión parcial del componente\(i\).

Ahora pretendemos que tenemos dos gases a la misma temperatura y presión, gas A y gas B. La energía Gibbs del sistema antes de que se mezclen los gases viene dada por la Ecuación\(\ref{1}\), que se puede combinar con la Ecuación\(\ref{4}\) para dar la expresión

\[G_{initial}=n_A(\mu^\circ_A+RT \ln P)+n_B(\mu^\circ_B+RT \ln P) \label{5}\]

Si el gas A y el gas B se mezclan entonces entre sí, cada uno ejercerá una presión parcial sobre el sistema total,\(P_A\) y\(P_B\), de manera que\(P_A+ P_B= P\). Esto significa que la energía final de Gibbs de la solución final se puede encontrar usando la ecuación

\[G_{final}=n_A(\mu^\circ_A+RT \ln P_A)+n_B(\mu^\circ_B+RT \ln P_B) \label{6}\]

La energía Gibbs de mezclar\(Δ_{mix}G\),, se puede encontrar luego restando\(G_{initial}\) de\(G_{final}\).

\[ \begin{align} Δ_{mix}G &= G_{final} - G_{initial}\\[4pt] &=n_ART \ln \frac{P_A}{P}+n_BRT \ln \frac{P_B}{P} \\[4pt] &=n_A RT \ln X_A+n_B RT \ln X_B \label{7} \end{align} \]

donde

\[P_i = X_iP\]

y\(X_i\) es la fracción molar de gas\(i\). Esta ecuación puede simplificarse aún más sabiendo que la fracción molar de un componente es igual al número de moles de ese componente sobre los moles totales del sistema, o

\[X_i = \dfrac{n_i}{n}.\]

La ecuación\ ref {7} luego se convierte en

\[\Delta_{mix} G=nRT(X_A \ln X_A + X_B \ln X_B) \label{8}\]

Esta expresión nos da el efecto que la mezcla tiene sobre la energía libre de Gibbs de una solución. Dado que\(X_A\) y\(X_B\) son fracciones molares que van de 0 a 1, podemos concluir que\(Δ_{mix}G \) será un número negativo. Esto es consistente con la idea de que los gases se mezclan espontáneamente a presión y temperatura constantes.

Entropía de mezcla

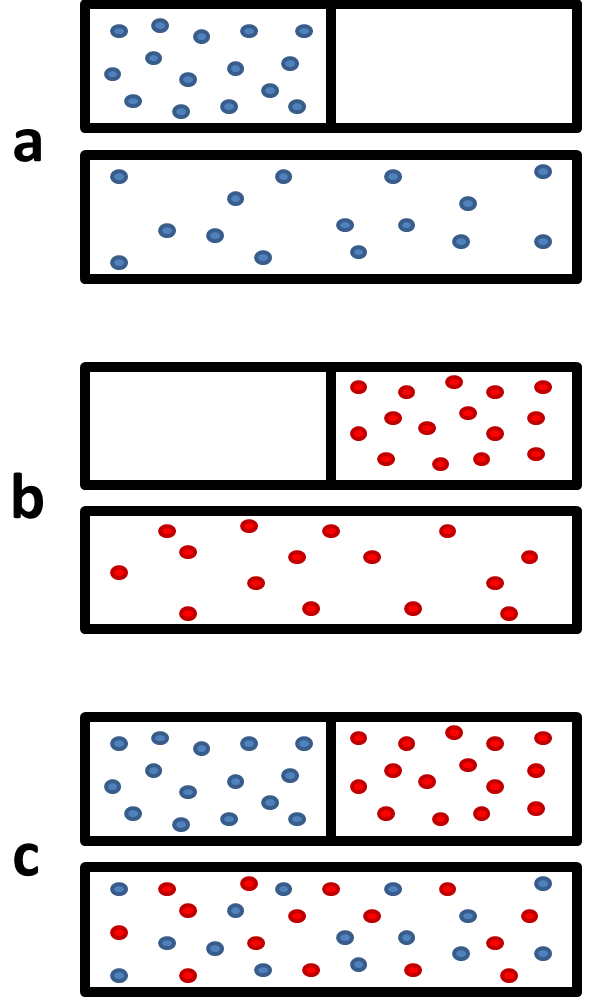
La figura\(\PageIndex{1}\) muestra que cuando dos gases se mezclan, realmente se puede ver como dos gases que se expanden al doble de su volumen original. Esto aumenta en gran medida el número de microestados disponibles, por lo que esperaríamos que también aumentara la entropía del sistema.

Figura\(\PageIndex{1}\): La mezcla de dos gases puede verse como dos expansiones. a) Expansión del gas A solo cuando se retira la barrera. Las moléculas tienen el doble de microestados en la caja abierta. b) Expansión del gas B a lo largo. c) la expansión simultánea de los gases A y B es equivalente a la mezcla

Los estudios termodinámicos de la dependencia de un gas ideal de la energía de temperatura libre de Gibbs han demostrado que

\[ \left( \dfrac {d G} {d T} \right )_P=-S \label{9}\]

Esto significa que diferenciar la Ecuación\(\ref{8}\) a presión constante con respecto a la temperatura dará una expresión del efecto que la mezcla tiene sobre la entropía de una solución. Vemos que

\[ \begin{align} \left( \dfrac {d G_{mix}} {d T} \right)_P &=nR(X_A \ln X_A+X_B \ln X_B) \\[4pt] &=-\Delta_{mix} S \end{align}\]

\[\Delta_{mix} S=-nR(X_A \ln X_A+X_2 \ln X_2) \label{10}\]

Dado que las fracciones molares vuelven a conducir a valores negativos para\(\ln X_A\) y\(\ln X_B\), el signo negativo frente a la ecuación hace\(\Delta_{mix} S\) positivo, como se esperaba. Esto concuerda con la idea de que la mezcla es un proceso espontáneo.

Entalpía de mezcla

Sabemos que en un sistema ideal\(\Delta G= \Delta H-T \Delta S\), pero esta ecuación también puede aplicarse a la termodinámica de la mezcla y resolverse para la entalpía de mezclar para que se lea

\[\Delta_{mix} H=\Delta_{mix} G+T\Delta_{mix} S \label{11}\]

Conectando nuestras expresiones para\(Δ_{mix}G\) (Ecuación\(\ref{8}\)) y\(Δ_{mix}S\) (Ecuación\(\ref{10}\)), obtenemos

\[\Delta_{mix} H=nRT(X_A \ln X_A+X_B \ln X_B)+T \left[-nR(X_A \ln X_A+X_B \ln X_B) \right] = 0\]

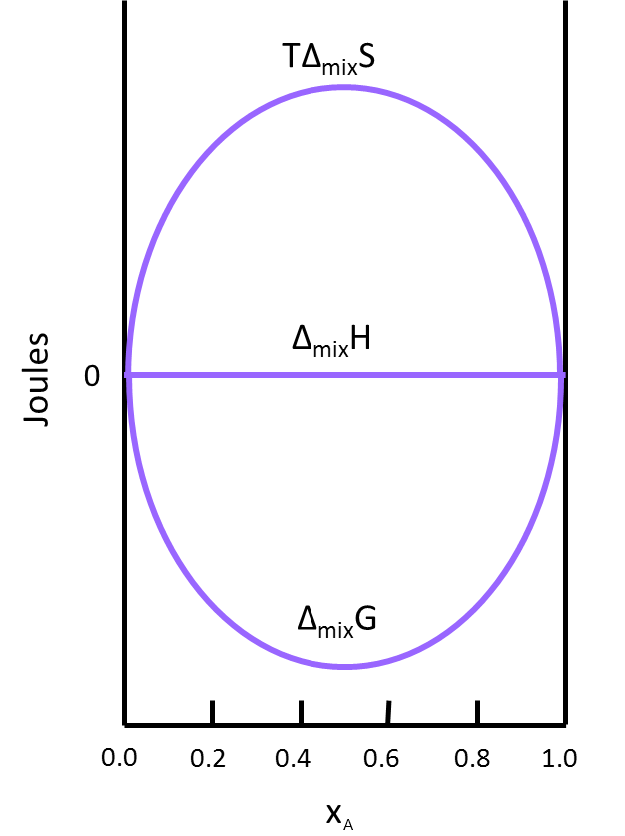
Este resultado tiene sentido a la hora de considerar el sistema. Las moléculas de gas ideal se extienden lo suficiente como para que no interactúen entre sí cuando se mezclan, lo que implica que no se absorbe ni se produce calor y resulta en un\(Δ_{mix}H\) de cero. La figura\(\PageIndex{2}\) ilustra cómo\(TΔ_{mix}S\) y\(Δ_{mix}G\) cambiar en función de la fracción molar para que\(Δ_{mix}H\) de una solución siempre sea igual a cero (esto es para la mezcla de dos gases ideales).

Figura\(\PageIndex{2}\): Una gráfica de\(T\Delta_{mix}S\),\(T\Delta_{mix}H\), y\(T\Delta_{mix}G\) en función de\(X_A\) para la mezcla de dos gases ideales.

Referencias

1. Chang, R. Química Física para las Biociencias, 1st Herdon, VA: Libros de Ciencias Universitarias, 132-133. Imprimir.
2. Meyer, E.F. (1987). Teromodinámica de “Mezcla” de Gases Ideales. J. Chem. Educ. 64, 676-677.

Enlaces externos

• Satter, S. (2000). Termodinámica de Mezclar Gases Reales. J. Chem. Educ. 77, 1361-1365.
• Brandani, V., Evangelista, F. (1987). Correlación y predicción de entalpías de mezcla para sistemas que contienen alcoholes con la teoría de soluciones asociadas UNIQUAC. Ind. Ing. Chem. Res. 26 (12), 2423—2430.

Problemas

1. Utilice la Figura 2 para encontrar el x ₁ que tiene el mayor impacto en las cantidades termodinámicas de la solución final. Explique por qué esto es cierto.
2. Calcular el efecto que tiene la mezcla de 2 moles de nitrógeno y 3 moles de oxígeno sobre la entropía de la solución final.
3. Otra forma de encontrar la entropía de un sistema es utilizando la ecuación ΔS = n Rln (V ₂ /V ₁). Utilice esta ecuación y el hecho de que el volumen es directamente proporcional al número de moles de gas a temperatura y presión constantes para derivar la expresión final para\(T\Delta_{mix}S\). (Pista: Utilice la derivación de\(T\Delta_{mix}G\) como guía).

RESPUESTAS

1. x ₁ = 0.5
2. Aumenta la entropía del sistema en 27.98 J/MOLK

Colaboradores

• Elizabeth Billquist (Colegio de la Esperanza)