2.6: Caracterización- Las matemáticas detrás de la cinética enzimática
- Page ID
- 78762
Parcelas de Michaelis-Menten
Una reacción catalizada por enzimas se puede dividir aproximadamente en tres etapas: unión enzima-sustrato, “catálisis” y liberación del producto. “Catálisis” se refiere a todos los pasos que suceden para convertir el sustrato en producto. A veces, estos pasos son demasiado rápidos para distinguirse unos de otros. Para simplificar, a veces nos referimos a toda esta secuencia de eventos como si fueran solo un paso.

A menudo, pero no siempre, esa parte de catálisis es el paso determinante de la velocidad. El lanzamiento del producto es una especie de ocurrencia tardía.
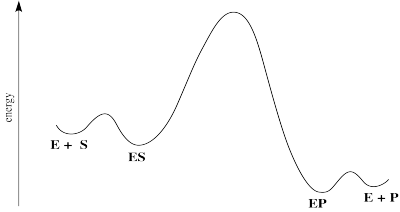
En ese caso, podríamos simplificar y solo considerar esos escalones a través de la catálisis.

Si hacemos eso, encontramos que las reacciones enzimáticas pueden resumirse mediante una relación llamada la ecuación de Michaelis-Menten, que lleva el nombre del bioquímico de principios del siglo XX Leonor Michaels y su colaborador, el inmensamente talentoso artista, médico y bioquímico, Maud Menten.

El numerador en esta ecuación debería tener sentido — por supuesto la tasa debería aumentar cuando agregamos más sustrato o más enzima y la relación dependerá de la velocidad de ese paso de formación del producto.
El denominador es un poco más complicado y contiene la constante compuesta K m, la constante de Michaelis-Menten.
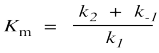
Esta relación se puede entender más fácilmente examinando sus límites. Por ejemplo, supongamos que la concentración de sustrato sigue siendo muy baja. Quizás sea mucho más pequeño que K m. ¿Cómo afecta eso a la velocidad de la reacción?
Es útil tener en cuenta que un gran número sumado a un número pequeño es solo un número grande. Un millón más uno es alrededor de un millón. Un millón más tres también es alrededor de un millón. Un millón más cinco está bastante cerca de un millón. A menudo podemos ignorar la pequeña cantidad en adiciones. En ese sentido, si [S] es pequeño, podemos ignorarlo en el denominador, y pensar en el denominador en cambio como “aproximadamente K m”.
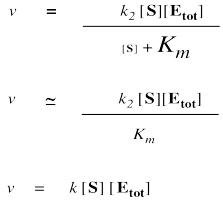
No podemos ignorar [S] en el numerador, claro, aunque sea muy pequeño. Eso es porque un número multiplicado por un número muy pequeño también se convierte en un número muy pequeño; el número pequeño realmente cuenta cuando se multiplica por algo.
Por otro lado, cuando [S] se vuelve muy grande, podemos ignorar el Km. Eso significa que Km desaparece del denominador, dejando sólo [S]. En ese punto, la [S] en el denominador y numerador cancela.

Recuerde, cuando [S] llega a ser muy grande, la reacción ha alcanzado su velocidad máxima posible, debido a que la enzima está saturada. Agregar más sustrato no acelera las cosas, porque el sustrato extra solo tiene que esperar hasta que una enzima esté disponible. A esa tasa máxima le llamamos V máx.
- Los límites de la ecuación de Michaelis Menten explican la forma de la curva describiendo la dependencia de la tasa en el sustrato.
Hay otra pieza de información útil que podemos obtener de esta ecuación. Viene en un punto intermedio entre los dos casos que hemos considerado hasta ahora. ¿Y si los valores numéricos de K m y [S] son exactamente iguales? En ese caso, el valor del denominador, K m + [S], es el mismo que [S] + [S]. El denominador se convierte en 2 [S]. Así como en el caso limitante que nos dio el valor de V max, el [S] cancela, pero esta vez todavía hay un 2 en el denominador, así obtenemos V max /2.
Dando la vuelta a esa conclusión, si encontramos el punto en una parcela de Michaelis Menten donde la tasa es la mitad de la tasa máxima, podemos bajar una línea hasta el eje x. El valor de [S] en la intercepción será numéricamente el mismo que el valor de Km.
- V max es el punto en el eje y donde la tasa se ha nivelado completamente.
- K m es el punto en el eje x correspondiente a y = V max /2.
Determinar V max y K m en cada uno de los siguientes casos. Supongamos que las unidades de [S] son milimoles por litro y las unidades de V son moles por litro por segundo.
a)
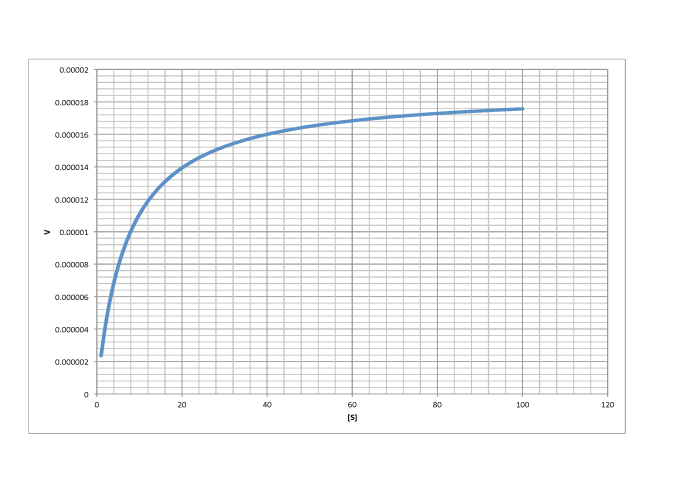
b)
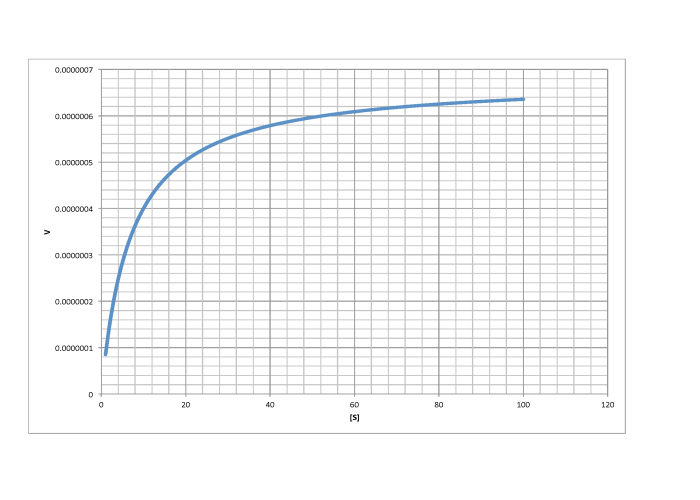
c)
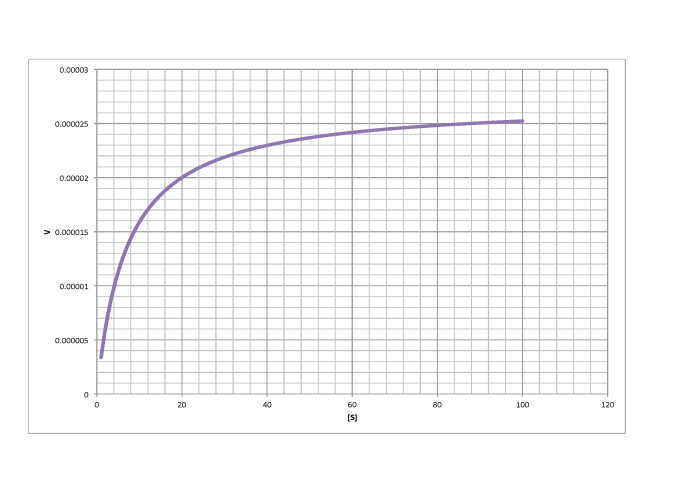
d)
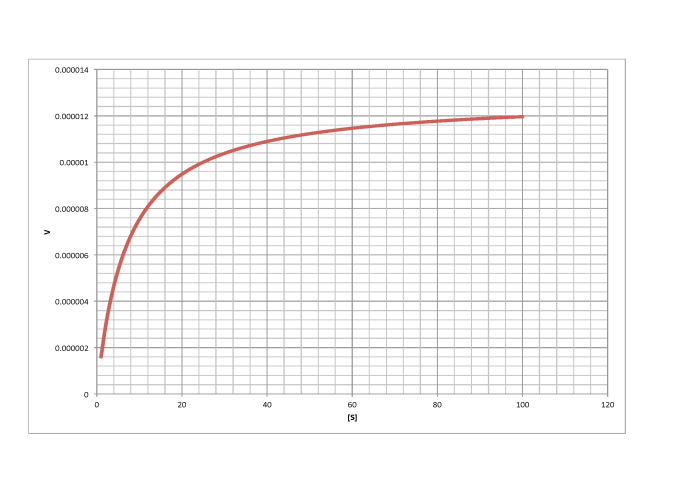
e)
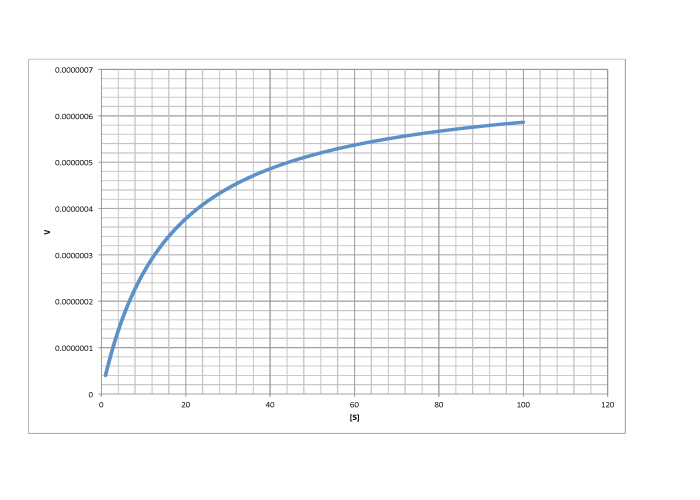
Contestar a-
\[V_{max} = 1.8 \times 10^{-5} \frac{mol}{L s} \nonumber\]
\[\frac{V_{max}}{2} = 9 \times 10^{-6} \frac{mol}{L s}\) so \(K_{m} = 6 \frac{mol}{L} \nonumber\]
- Respuesta b
-
\[V_{max} = 6.5 \times 10^{-7} \frac{mol}{L s} \nonumber\]
\[\frac{V_{max}}{2} = 3.25 \times 10^{-7} \frac{mol}{L s}\) so \(K_{m} = 7 \frac{mol}{L} \nonumber\]
- Respuesta c
-
\[V_{max} = 2.6 \times 10^{-5} \frac{mol}{L s} \nonumber\]
\[\frac{V_{max}}{2} = 1.3 \times 10^{-5} \frac {mol}{L s}\) so \(K_{m} = 6 \frac{mol}{L} \nonumber\]
- Respuesta d
-
\[V_{max} = 1.2 \times 10^{-5} \frac{mol}{L s} \nonumber\]
\[\frac{V_{max}}{2} = 6 \times 10^{-6} \frac{mol}{L s}\) so \(K_{m} = 6 \frac{mol}{L} \nonumber\]
- Respuesta e
-
\[V_{max} = 6.0 \times 10^{-7} \frac{mol}{L s} \nonumber\]
\[\frac{V_{max}}{2} = 3 \times 10^{-7} \frac {mol}{L s}\) so \(K_{m} = 13 \frac {mol}{L} \nonumber\]
Frecuencia de rotación y eficiencia
Si estamos realizando un experimento, sabemos cuál es la concentración total de enzima, porque somos nosotros los que la metemos ahí. Eso significa que también podemos averiguar exactamente cuál es esa constante de velocidad para la catálisis.
\[k_{cat} = k_{2} = \frac{V_{max}}{\mathbf{[E_{tot}]}} \nonumber\]
Esa cantidad, k cat, a veces es referida por los bioquímicos como el “número de facturación”. El número de recambio significa esencialmente el número de moléculas de producto elaboradas por una enzima en el periodo de tiempo especificado (generalmente las unidades de k cat se expresan como s -1, pero también podrían escribirse en min -1, etc.).
En la catálisis industrial, k cat en cambio se conoce como la “frecuencia de rotación”, pero por supuesto todavía significa lo mismo. Hay una razón importante para esta diferencia de términos. El “número de facturación” en la industria se refiere al número de moléculas de producto elaboradas antes de que el catalizador deje de funcionar. La muerte del catalizador puede ocurrir por varias razones, pero podrías imaginar que algo va mal a través de una reacción secundaria que hace que el catalizador no reaccione hacia el sustrato. Esta es una consideración muy importante en la industria. El ingeniero a cargo de la planta de producción quisiera reemplazar el catalizador por un nuevo lote antes de que deje de funcionar, para evitar una parada no programada en el proceso que podría resultar muy costosa. Necesitan tener una idea sobre cuándo es probable que eso suceda, por lo que deben estar al tanto del número de facturación en este sentido.
Otra consideración que a veces es útil es la eficiencia enzimática. Recuerde, la reacción no depende sólo del paso de catálisis. El paso vinculante también importa. Cuanto más rápido sea el paso de catálisis, más rápida será la producción de producto. Además, cuanto mayor sea la proporción de sustrato unido, más rápida será la producción del producto.
Combinando esas dos ideas:
\[Efficiency = \frac{k_{cat}}{K_{m}} \nonumber\]
En esta relación, Km es un sustituto de la constante de equilibrio para la disociación enzima-sustrato. No es exactamente lo mismo, pero es lo más cercano que tenemos. Por extensión, 1/ K m representa la constante de unión enzima-sustrato. Cuanto mayor sea la constante de unión y más rápida sea la catálisis, más eficiente será la enzima.
Obsérvese que las unidades de K m son unidades de concentración (mol L -1, por ejemplo). Por lo tanto, las unidades de eficiencia serán algo así como L mol -1 s -1.
Parcelas Lineweaver-Burk
La ecuación de Michaelis-Menten también es útil de otras maneras. Si tomamos su inversa, obtenemos una nueva relación.
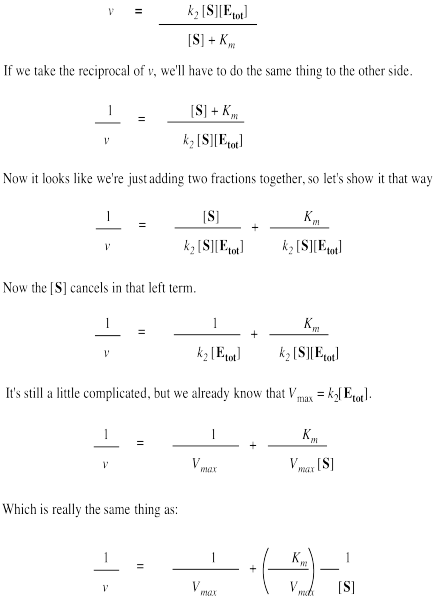
Eso es útil porque es realmente una expresión para una línea recta. Si trazamos 1/v contra 1/ [S], obtenemos una línea recta. La pendiente es K m/V max y la intercepción y es 1/ V max.
- La gráfica Lineweaver-Burk da una línea recta para los datos de velocidad.
- y intercepción = 1/ V máx
- pendiente = K m /V máx
- la intercepción x = -1/ K m, también
Determinar los valores de Vmax y Km en cada uno de los siguientes casos. Supongamos que las unidades de [S] son milimoles por litro y las unidades de V son moles por litro por segundo.
a)
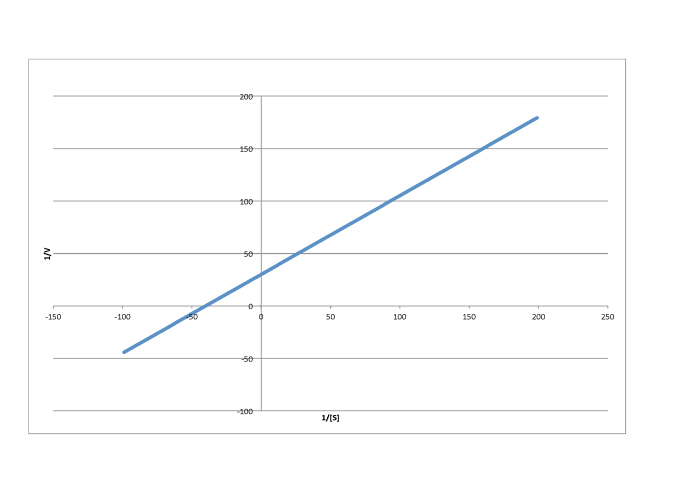
b)
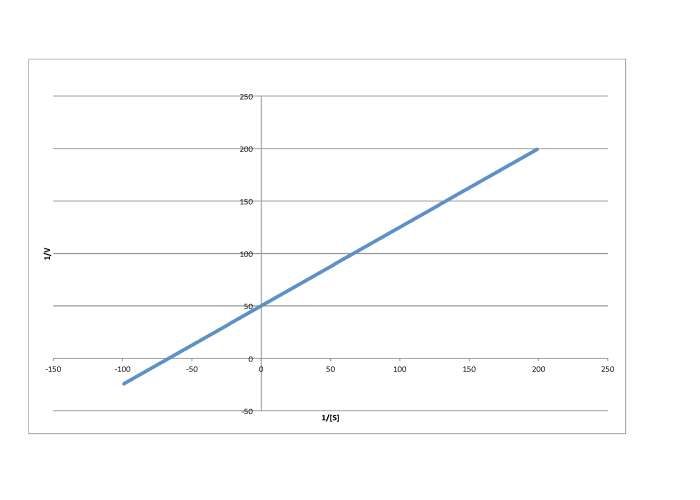
c)
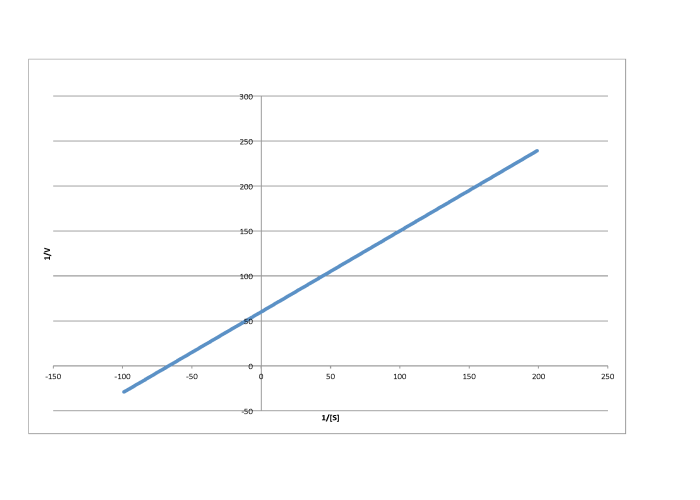
d)
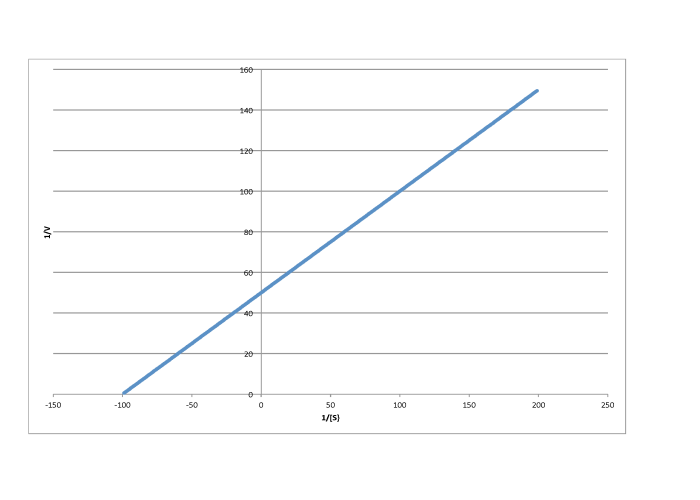
e)
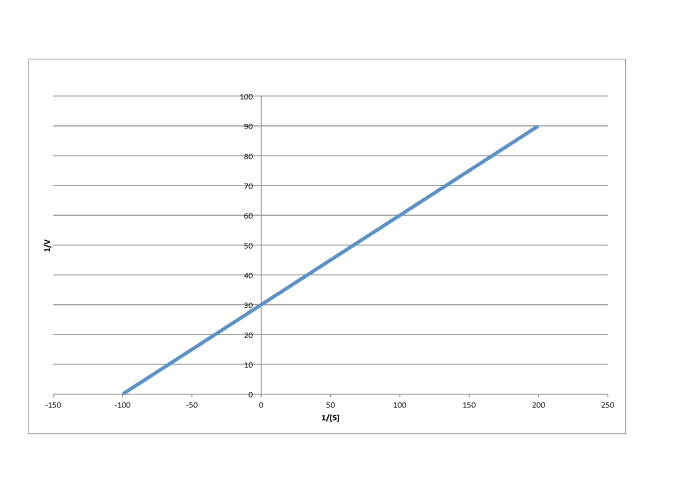
f)
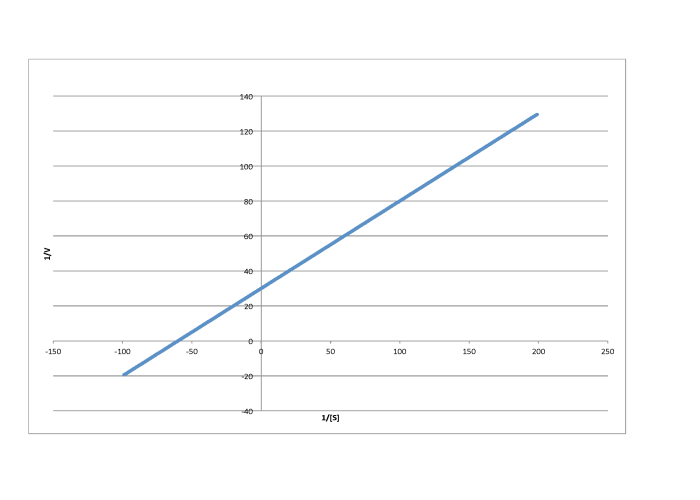
Contestar a-
\[\frac{1}{V_{max}} = 30 \frac{ L s}{mol}\) so \(V_{max} = 3.3 \times 10^{-2} \frac {mol}{L s} \nonumber\]
\[\frac{-1}{K_{m} = -40 \frac{L}{mmol}\) so \(K_{m} = 2.5 \times 10^{-2} \frac{M}{L} \nonumber\]
- Respuesta b
-
\[\frac{1}{V_{max}} = 50 \frac{L s}{mol}\) so \(V_{max} = 2.- \times 10^{-2} \frac{mol}{L s} \nonumber\]
\(\frac{-1}{K_{m} = -70 \frac{L}{mmol}\)por lo\(K_{m} = 1.4 \times 10^{-2} \frac{M}{L}\)
- Respuesta c
-
\[\frac{1}{V_{max} = 60 \frac{L s}{mol}\) so \(V_{max} = 1.7 \times 10^{-2} \frac{mol}{L s} \nonumber\]
\(\frac{-1}{K_{m}} = -70 \frac{L}{mmol}\)por lo\( K_{m} = 1.4 \times 10^{-2} \frac{M}{L}\)
- Respuesta d
-
\[\frac{1}{V_{max}} = 50 \frac{L s}{mol}\) so \(V_{max} = 2.0 \times 10^{-2} \frac{mol}{L s} \nonumber\]
\(\frac{-1}{K_{m}} = -100 \frac {L}{mmol}\)por lo\(K_{m} = 1.0 \times 10^{-2} \frac{M}{L}\)
- Respuesta e
-
\[\frac{1}{V_{max}} = 30 \frac{L s}{mol}\) so \(V_{max} = 3.3 \times 10^{-2} \frac {mol}{L s} \nonumber\]
\(\frac{-1}{K_{m}} = -100 \frac{L}{mmol}\)por lo\(K_{m} = 1.0 \times 10^{-2} \frac{M}{L}\)
- Respuesta f
-
\[\frac{1}{V_{max}} = 30 \frac{L s}{mol}\) so \(V_{max} = 3.3 \times 10^{-2} \frac{mol}{L s} \nonumber\]
\(\frac{-1}{K_{m}} = -60 \frac{L}{mmol}\)por lo\(K_{m} = 1.7 \times 10^{-2} \frac{M}{L}\)
Parcelas de Inhibición y Lineweaver-Burk
Las gráficas Lineweaver-Burk permiten una visión adicional del mecanismo de inhibición. La siguiente gráfica, por ejemplo, muestra inhibición competitiva.
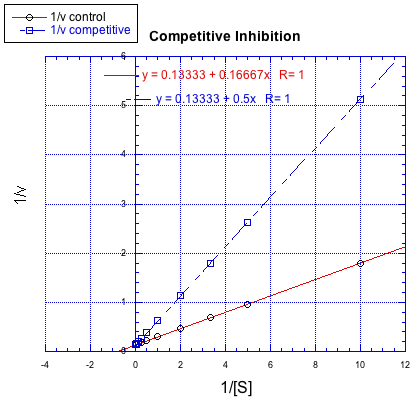
Debido a que la gráfica usa 1/v en el eje y, la reacción más lenta es en realidad la línea superior. La conclusión es la reacción regular sin un inhibidor. Recuerde, la intercepción y es igual a 1/ V máx. En la inhibición competitiva, la reacción inhibida finalmente alcanza (o al menos se acerca) al mismo V max que la reacción desinhibida. La gráfica Lineweaver-Burk muestra que ambas líneas se encuentran con el eje y en el mismo lugar.
En contraste, la siguiente gráfica muestra inhibición no competitiva. Una vez más, la línea regular es la inferior, mientras que la línea superior es la inhibida. Las dos líneas no comparten la misma e intercepción, sin embargo. No obstante, sí comparten la misma intercepción x. Eso se debe a que la inhibición no competitiva no afecta directamente la unión del sustrato (que se refleja en Km), sino que interfiere con la etapa de catálisis (ligada a V max).
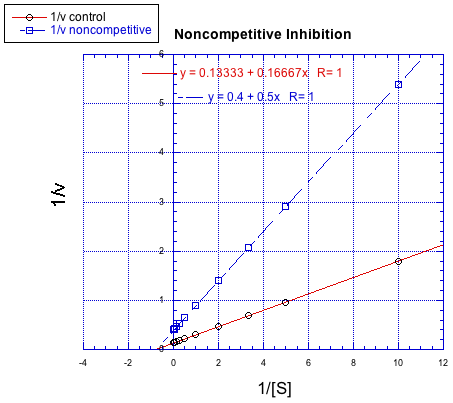
La diferencia entre inhibición no competitiva y no competitiva, muy sutil en una trama de Michaelis-Menten, es bastante clara en Lineweaver-Burk. El caso que se ilustra a continuación es considerado como inhibición no competitiva “pura”. Una vez más, la reacción inhibida se muestra por la línea superior. En este caso, las reacciones inhibidas y desinhibidas producen líneas paralelas en la gráfica Lineweaver-Burk; esa característica es en realidad la definición de inhibición no competitiva.
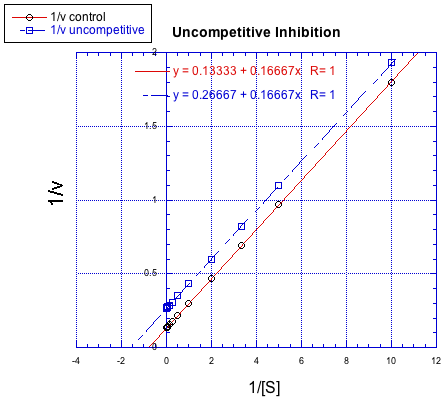
Si lo piensas, la inhibición pura no competitiva solo ocurre bajo circunstancias muy específicas. El K m difiere claramente cuando se agrega un inhibidor; podemos verlo en la diferente x intercepción. No obstante, la pendiente es la misma. La inclinación es K m/V max. Eso significa que, debido a que K m es diferente, V max debe diferir exactamente de la misma manera, manteniendo la pendiente igual. Por ejemplo, si K m se corta a la mitad en la reacción inhibida, entonces V max también se debe cortar por la mitad. Eso mantendría igual la pendiente.
Por otro lado, una situación en la que la reacción inhibida no da una línea paralela a la reacción regular se denomina “inhibición mixta”. Al igual que la inhibición no competitiva, la inhibición mixta da como resultado cambios tanto en K m como en V máx. Sin embargo, los cambios en este caso no escalan exactamente de la misma manera que en la inhibición no competitiva.
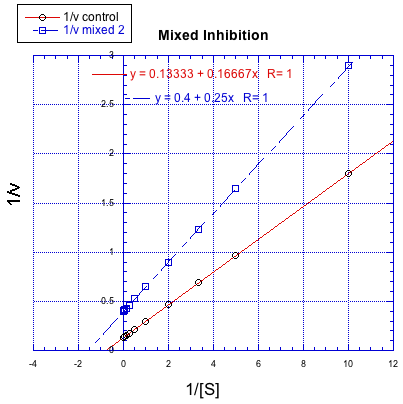
Caracterizar cada una de las siguientes gráficas como una inhibición competitiva, no competitiva, no competitiva o mixta.
a)
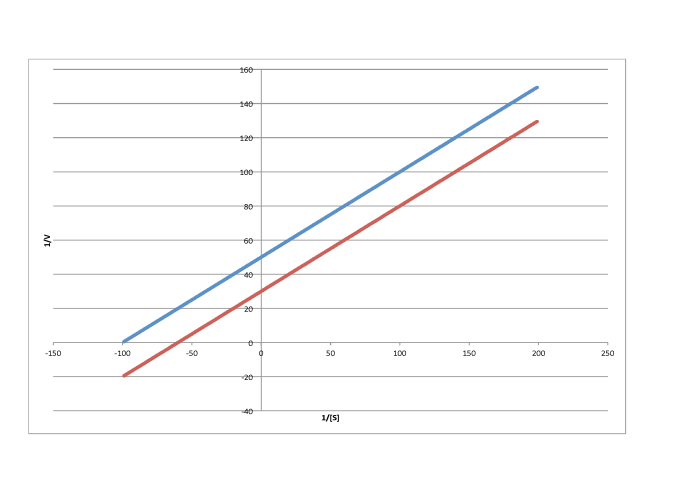
b)
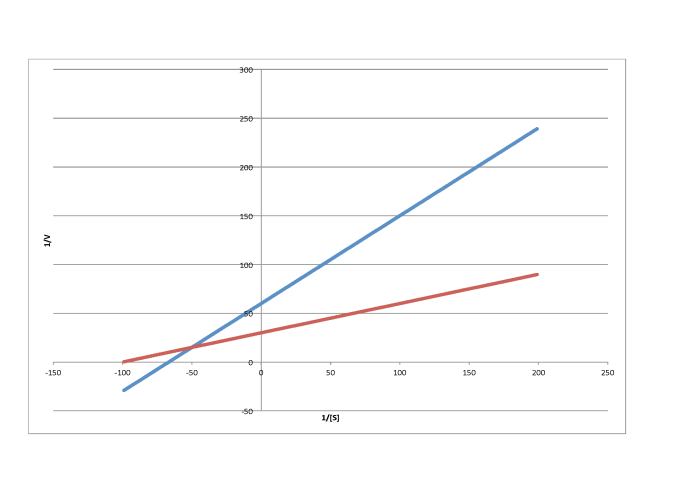
c)
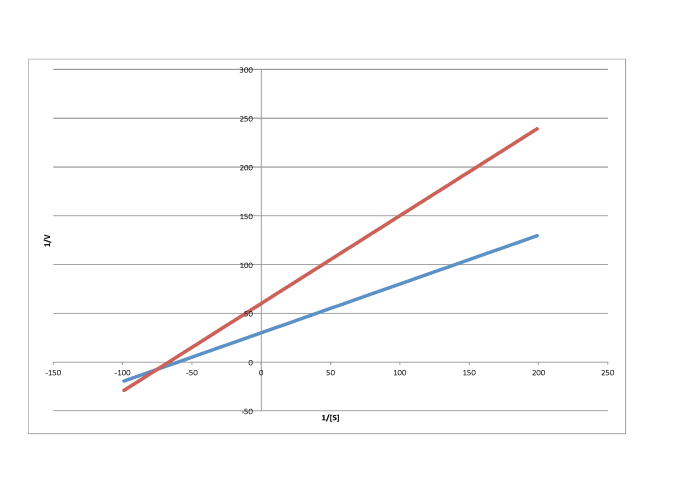
d)
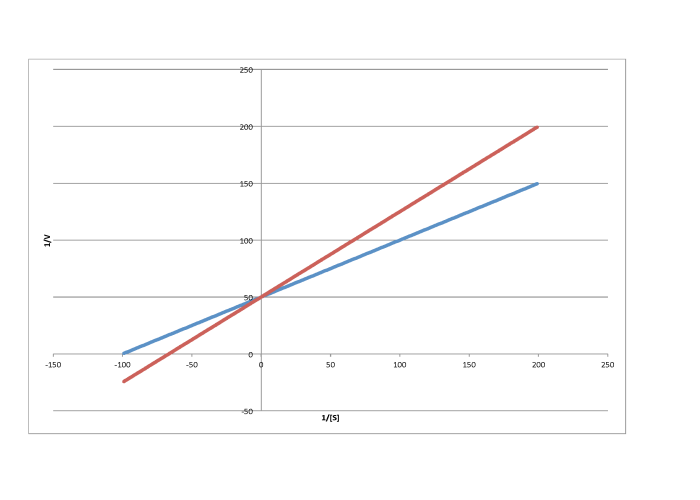
e)
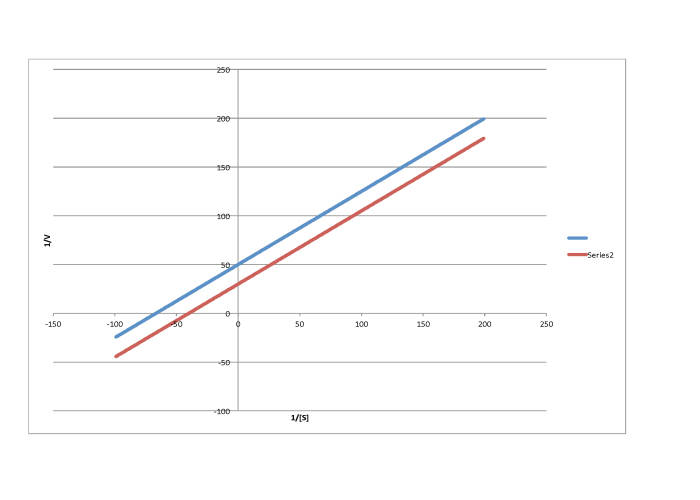
f)
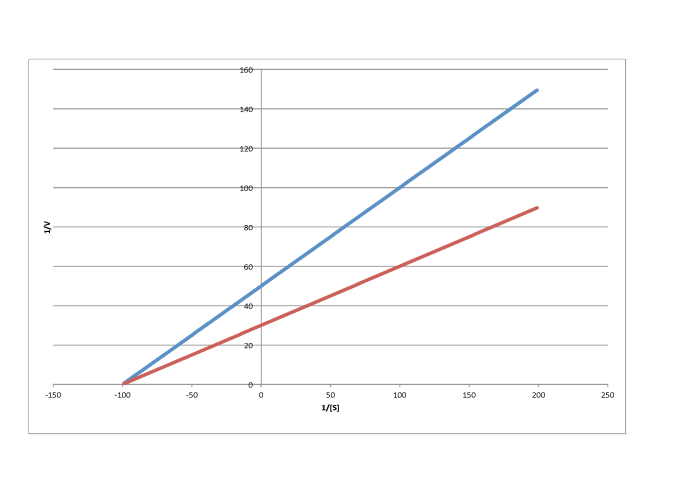
g)
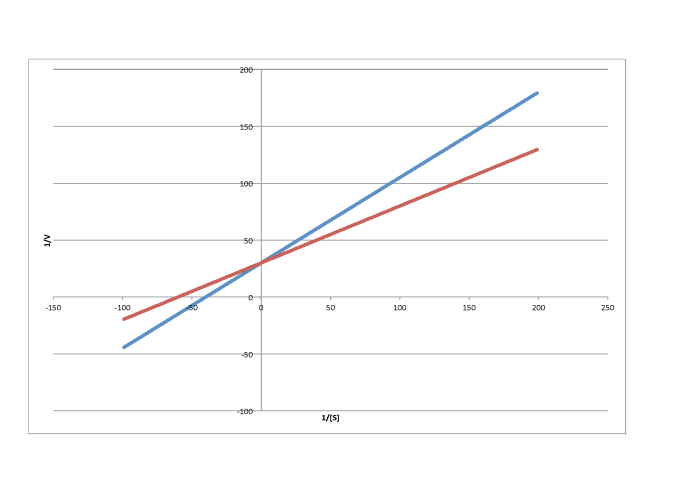
Contestar a-
no competitivo
- Respuesta b
-
mixto
- Respuesta c
-
no competitivo
- Respuesta d
-
competitivo
- Respuesta e
-
no competitivo
- Respuesta f
-
no competitivo
- Respuesta g
-
competitivo
El origen de la ecuación de Michaelis-Menten
Pero, ¿de dónde viene la relación Michaelis-Menten? Eso requiere un poco de trabajo pesado con cinética. Si sientes la necesidad de saber, entonces comenzaremos con la aproximación de que la reacción esencialmente se reduce a dos pasos: la unión al sustrato y las cosas posteriores a eso. El paso de unión se describe como k 1 /k -1. El material después de eso se resume en k 2.
La tasa de formación del producto realmente depende de la tasa del paso elemental k 2. Esa velocidad depende de la cantidad de complejo de sustrato enzimático y su velocidad de paso a través de la etapa posterior.
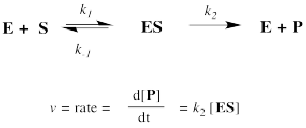
El problema es que el complejo enzimático sustrato es un intermedio. No sabemos exactamente cuánto tenemos. Podríamos suponer que, como intermedio reactivo, el complejo no tiene mucha vida. Se agota más o menos en cuanto se forma.
Esa suposición nos ayuda a expresar la concentración del complejo enzimático sustrato en términos de otras cosas que podríamos conocer más: la enzima y el sustrato. Por supuesto, la enzima y el sustrato reaccionan juntos para hacer complejo el sustrato enzimático. Reaccionan junto con constante de velocidad k 1.
Dos posibles destinos esperan el complejo enzimático sustrato. O se libera de nuevo a enzima y sustrato libre, con constante de velocidad k -1, o bien pasa a hacer producto, con constante de velocidad k 2. En una aproximación en estado estacionario, el complejo enzimático sustrato se consume tan pronto como se forma.
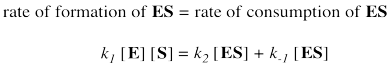
Nuevamente, no sabemos cuánta enzima libre hay. No sabemos cuánto complejo enzima-sustrato tenemos. Sabemos cuánta enzima se agrega al inicio del experimento cinético. Llamaremos a esa concentración [E tot], es decir, la cantidad total de enzima. Parte de esa enzima permanece libre, y parte de ella se une como complejo enzima-sustrato.
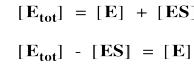
Es útil expresar la concentración de enzima libre como la enzima total menos esa porción unida al sustrato. De esa manera, podremos eliminar el término para enzima libre de la ecuación de velocidad. Unos pocos pasos de álgebra permiten expresar la concentración del complejo enzima-sustrato únicamente en términos de la concentración total de enzima, la concentración de sustrato y algunas constantes de velocidad.
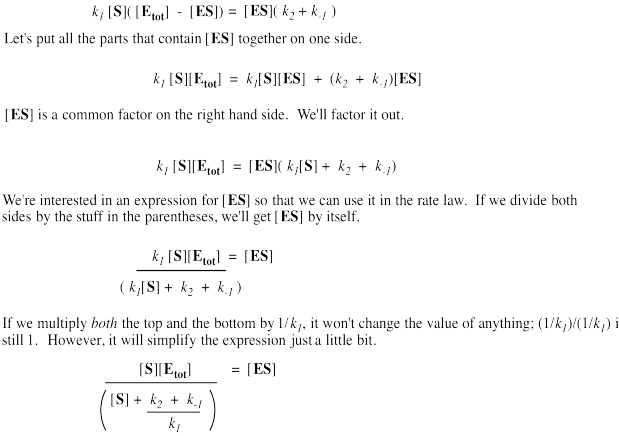
Recuerde, la velocidad de formación del producto solo depende de la cantidad de complejo enzima-sustrato y la constante de velocidad para la etapa de catálisis.

Esa colección de constantes en el denominador no es más que un grupo de números. Es una constante. La llamaremos la constante Michaelis-Menten.
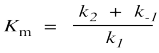
Eso nos devuelve a la ecuación de Michaelis-Menten.


