5.5: Mecánica de Ondas

A mediados de los años veinte algunos científicos comenzaron a darse cuenta de que los electrones deben moverse alrededor del núcleo de una manera muy diferente a aquella en la que los planetas se mueven alrededor del sol. Abandonaron la idea de que un electrón traza una órbita o trayectoria definida. En cambio adoptaron el punto de vista de que era imposible describir la trayectoria exacta de una partícula cuya masa era tan pequeña como la de un electrón. En lugar de pensar en el movimiento en términos planetarios, sugirieron que era mucho más útil pensar en este movimiento en términos de una onda que podría doblarse alrededor del núcleo solo en ciertos patrones tridimensionales específicos. Esta nueva forma de abordar el comportamiento de los electrones (y también de otras partículas) se conoció como mecánica de ondas o mecánica cuántica. Para familiarizarte con algunos de los conceptos y terminología de la mecánica de olas, consideraremos el ejemplo simple, aunque algo artificial, ilustrado en la Figura 1. Esto generalmente se conoce como una partícula en una caja unidimensional. Consideramos que la partícula (que podría ser un electrón) tiene una masa m y está restringida en su movimiento por un tubo estrecho pero absolutamente recto de longitud d en el que simplemente puede encajar. Este contenedor, o caja, está cerrado en ambos extremos y asegura que la partícula pueda moverse en una sola dimensión dentro de su longitud.

Figura\(\PageIndex{1}\) Una partícula microscópica en una caja unidimensional de longitud d. (a) Analogía con una bola de billar macroscópica: (b), (c) y (d), analogía con las ondas en una cuerda de guitarra vibrante; (e) un ejemplo de una onda que no encajaría en la caja. El extremo derecho se movería hacia arriba y hacia abajo en lugar de permanecer fijo como en las partes (b), (c) y (d).

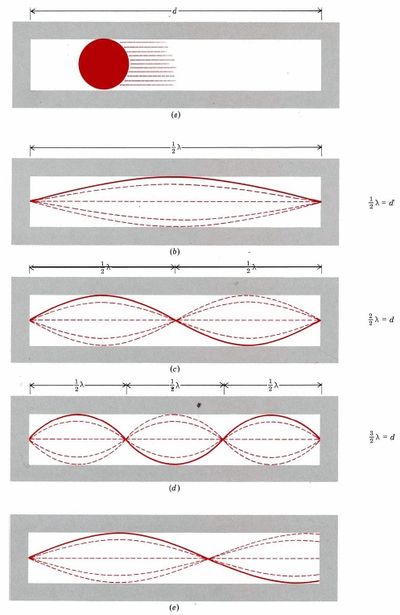
Un objeto cotidiano como una canica o una bola de billar podría moverse de un lado a otro en este contenedor, rebotando en cualquiera de los extremos. Si no hubiera fricción para ralentizarlo, la partícula oscilaría indefinidamente, manteniendo una velocidad constante v y una energía cinética constante E _k de valor ½ m v ². La magnitud real de v (y por lo tanto E _k) dependería de cuán grande o de pequeño tamaño se le diera inicialmente un “empuje” a la partícula, para comenzar a moverse.

Para observar esta partícula desde un punto de vista onda-mecánico, aplicamos una idea originalmente sugerida en 1924 por Louis de Broglie (1892 a 1987). Propuso que una onda de longitud de onda λ se asocia con cada partícula. Cuanto mayor es la masa de la partícula y más rápido se mueve, más pequeña se vuelve esta longitud de onda. La relación exacta viene dada por la fórmula

\[\lambda =\dfrac{h}{\mu} \label{1} \]

donde μ es el momento del electrón, el producto de su masa y velocidad (μ = m * v) y la constante de proporcionalidad h se conoce como constante de Planck (h = 6.626 × 10 ^—34 J s). La vista onda-mecánica ya no representa la partícula como la bola de billar oscilante de la Figura\(\PageIndex{1}\) a. En cambio debemos comenzar a pensar que tiene un comportamiento similar al de la cuerda de guitarra ilustrada en la Figura\(\PageIndex{1}\) b, c o d. En otra parte se puede ver una serie de videos que demuestran y describen los aspectos de la mecánica de olas. Muestran las diferentes longitudes de onda que pueden estar formadas por una cuerda anclada en ambos extremos. Si la cuerda está unida a ambos extremos de la caja, solo son posibles aquellas ondas o vibraciones en las que los extremos de la cuerda no se mueven. La longitud d de la caja puede corresponder así a una sola media longitud de onda (Figura\(\PageIndex{1}\) b), a dos medias longitudes de onda (Figura\(\PageIndex{1}\) c), a tres medias longitudes de onda (Figura\(\PageIndex{1}\) d, etc., pero no a la situación intermedia mostrada en la Figura \(\PageIndex{1}\)e. En otras palabras, la longitud del tubo debe corresponder a un número entero de medias longitudes de onda, o

\[d=n\dfrac{\lambda}{\text{2}} \label{2} \]

donde n = 1, 2, 3, 4, o algún número entero mayor. Si n = 1, d = λ/2; si n = 2, d = λ; y así sucesivamente. Reordenando la ecuación\(\ref{2}\), luego obtenemos

\[\lambda =\dfrac{\text{2}d}{n} \label{3} \]

Dado que los lados de la derecha de las Ecuaciones\(\ref{1}\) y\(\ref{3}\) son ambos iguales a λ, se pueden establecer iguales entre sí, dando

\[\dfrac{\text{2}}{n} d = \dfrac{h}{\mu} = \dfrac{h}{mv} \nonumber \]

que reorganiza para dar

\[v=\dfrac{nh}{\text{2}md} \text{ } n = \text{1, 2, 3, 4,} \ldots \nonumber \]

Ahora podemos calcular la energía cinética de nuestra ondapartícula. Está dado por la fórmula

\[E_{k}=\tfrac{\text{1}}{\text{2}}mv^{\text{2}}=\tfrac{\text{1}}{\text{2}}m\left( \dfrac{nh}{\text{2}md} \right)^{\text{2}} \nonumber \]

o

\[E_{k}=n^{\text{2}}\left( \dfrac{h^{\text{2}}}{\text{8}md^{\text{2}}} \right) \label{4} \]

Dado que el valor de n se restringe a números enteros positivos, llegamos al interesante resultado de que la energía cinética del electrón solo puede tener ciertos valores y no otros. Así, si nuestra partícula es un electrón (m = 9.1 × 10 ^—31 kg) y la caja unidimensional es aproximadamente del tamaño de un átomo (d = 1 × 10 ^—10 m), los valores permitidos de la energía están dados por

\[E_{k}=n^{\text{2}}\left( \dfrac{h^{\text{2}}}{\text{8}md^{\text{2}}} \right)=n^{\text{2}}\text{ }\times \text{ }\dfrac{\text{(6}\text{.624 }\times \text{ 10}^{-\text{34}}\text{ J s)}^{\text{2}}}{\text{8 }\times \text{ 9}\text{.1 }\times \text{ 10}^{-\text{31}}\text{ kg }\times \text{ 1 }\times \text{ 10}^{-\text{20}}\text{ m}^{\text{2}}} \nonumber \]

\[=n^{\text{2}}\text{ }\times \text{ 6}\text{.0 }\times \text{ 10}^{-\text{18}}\text{ }\dfrac{\text{J}^{\text{2}}\text{ s}^{\text{2}}}{\text{kg m}^{\text{2}}}=n^{\text{2}}\text{ }\times \text{ 6}\text{.0 }\times \text{ 10}^{-\text{18}}\text{ J} \nonumber \]

\[\text{ (recall: 1 J}=\text{1 kg m}^{\text{2}}\text{ s}^{-\text{2}}\text{)} \nonumber \]

Así, si n = 1, E _k = 1 ² × 6.0 × 10 ^—18 J = 6.0 aJ

Si n = 2, E _k = 2 ² × 6.0 × 10 ^—18 J = 24.0 aJ

Si n = 3, E _k = 3 ² × 6.0 × 10 ^—18 J = 54.0 aJ

y así sucesivamente.

Este resultado significa que al tratar al electrón como una onda, su energía se restringe automáticamente a ciertos valores específicos y no a los intermedios. Aunque el electrón puede tener una energía de 6.0 o 24.0 attojulios (aJ), no puede tener una energía intermedia como 7.3 o 11.6 aJ. Describimos esta situación diciendo que se cuantifica la energía del electrón. Ahora podemos comenzar a vislumbrar algunas de las ventajas de mirar el electrón en términos ondas-mecánicos. Si un electrón es en cierto sentido una onda, entonces solo son posibles ciertos tipos de movimiento, es decir, solo ciertos tipos de patrones de onda, gobernados por números enteros. Como veremos en breve, cuando se permite que un electrón se mueva en tres dimensiones alrededor de un núcleo, este tipo de comportamiento se traduce fácilmente en una estructura de concha. Un electrón puede estar en el caparazón 1 o el caparazón 2 pero no en un caparazón intermedio como 1.386. Una propiedad más del electrón surge de la analogía de onda. Si el electrón en una caja se comporta como una cuerda de guitarra, ya no podemos afirmar que el electrón se encuentra en una posición específica dentro de la caja o se mueve en una dirección u otra. ¡De hecho el electrón parece estar por toda la caja a la vez! Todo lo que podemos decir es que la onda (o la vibración de la cuerda) tiene cierta intensidad en cualquier punto a lo largo de la caja. Esta intensidad es mayor en algunos lugares que en otros y siempre es cero en ambos extremos de la caja.