3.2: El modelo Bohr

Última actualización
Guardar como PDF

Page ID: 77618

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Describir el modelo Bohr del átomo de hidrógeno
Utilice la ecuación de Rydberg para calcular las energías de luz emitidas o absorbidas por los átomos de hidrógeno

Siguiendo la obra de Ernest Rutherford y sus colegas a principios del siglo XX, estaba bien establecida la imagen de átomos consistentes en diminutos núcleos densos rodeados de electrones más ligeros y aún más pequeños que se movían continuamente alrededor del núcleo. A esta imagen se le llamó el modelo planetario, ya que imaginaba al átomo como un “sistema solar” en miniatura con los electrones orbitando el núcleo como planetas orbitando el sol. El átomo más simple es el hidrógeno, que consiste en un solo protón como núcleo alrededor del cual se mueve un solo electrón. La fuerza electrostática que atrae el electrón al protón depende únicamente de la distancia entre las dos partículas.

\[ F_{gravity} = G \dfrac{ m_1 m_2}{r^2} \nonumber \]

con

\(G\)es una constante gravitacional
\(m_1\)y\(m_2\) son las masas de partícula 1 y 2, respectivamente
\(r\)es la distancia entre las dos partículas

La fuerza electrostática tiene la misma forma que la fuerza gravitacional entre dos partículas másicas excepto que la fuerza electrostática depende de las magnitudes de las cargas sobre las partículas (+1 para el protón y -1 para el electrón) en lugar de las magnitudes de las masas de partículas que gobiernan la gravitacional fuerza.

\[ F_{electrostatic} = k \dfrac{ m_1 m_2}{r^2} \nonumber \]

con

\(k\)es una constante
\(m_1\)y\(m_2\) son las masas de partícula 1 y 2, respectivamente
\(r\)es la distancia entre las dos partículas

Dado que las fuerzas pueden derivarse de potenciales, es conveniente trabajar con potenciales en su lugar, ya que son formas de energía. El potencial electrostático también se llama potencial de Coulomb. Debido a que el potencial electrostático tiene la misma forma que el potencial gravitacional, según la mecánica clásica, las ecuaciones de movimiento deben ser similares, con el electrón moviéndose alrededor del núcleo en órbitas circulares o elípticas (de ahí la etiqueta modelo “planetario” del átomo). Los potenciales de la forma V (r) que dependen únicamente de la distancia radial\(r\) se conocen como potenciales centrales. Los potenciales centrales tienen simetría esférica, por lo que en lugar de especificar la posición del electrón en las coordenadas cartesianas habituales (x, y, z), es más conveniente usar coordenadas esféricas polares centradas en el núcleo, consistentes en una coordenada lineal r y dos coordenadas angulares, generalmente especificadas por las letras griegas theta (θ) y phi (Φ). Estas coordenadas son similares a las utilizadas en los dispositivos GPS y la mayoría de los teléfonos inteligentes que rastrean posiciones en nuestra tierra (casi) esférica, con las dos coordenadas angulares especificadas por la latitud y longitud, y la coordenada lineal especificada por la elevación del nivel del mar. Debido a la simetría esférica de los potenciales centrales, la energía y el momento angular del átomo de hidrógeno clásico son constantes, y las órbitas están obligadas a quedar en un plano como los planetas que orbitan el sol. Esta descripción mecánica clásica del átomo es incompleta, sin embargo, ya que un electrón que se mueve en una órbita elíptica estaría acelerando (cambiando de dirección) y, según el electromagnetismo clásico, debería emitir continuamente radiación electromagnética. Esta pérdida de energía orbital debería dar como resultado que la órbita del electrón se haga cada vez más pequeña hasta que se enrolla en espiral hacia el núcleo, lo que implica que los átomos son inherentemente inestables.

En 1913, Niels Bohr intentó resolver la paradoja atómica ignorando la predicción del electromagnetismo clásico de que el electrón en órbita en hidrógeno emitiría luz continuamente. En cambio, incorporó a la mecánica clásica la descripción de las ideas de cuantificación del átomo de Planck y el hallazgo de Einstein de que la luz consiste en fotones cuya energía es proporcional a su frecuencia. Bohr asumió que el electrón que orbita el núcleo normalmente no emitiría ninguna radiación (la hipótesis del estado estacionario), sino que emitiría o absorbería un fotón si se movía a una órbita diferente. La energía absorbida o emitida reflejaría diferencias en las energías orbitales según esta ecuación:

\[ |ΔE|=|E_f−E_i|=h u=\dfrac{hc}{\lambda} \label{6.3.1} \]

En esta ecuación, h es la constante de Planck y E _i y E _f son las energías orbitales inicial y final, respectivamente. Se utiliza el valor absoluto de la diferencia de energía, ya que las frecuencias y longitudes de onda son siempre positivas. En lugar de permitir valores continuos para el momento angular, la energía y el radio de órbita, Bohr asumió que solo podrían ocurrir valores discretos para estos (en realidad, cuantificar cualquiera de estos implicaría que los otros dos también están cuantificados). La expresión de Bohr para las energías cuantificadas es:

\[E_n=−\dfrac{k}{n^2} \label{6.3.2} \]

con\(n=1,2,3, ...\)

En esta expresión,\(k\) es una constante que comprende constantes fundamentales como la masa y carga de electrones y la constante de Planck. Insertar la expresión de las energías orbitales en la ecuación para\(ΔE\) da

\[ \color{red} ΔE=k \left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right)=\dfrac{hc}{\lambda} \label{6.3.3} \]

\[ \dfrac{1}{\lambda}=\dfrac{k}{hc} \left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right) \label{6.3.4} \]

Los pocos niveles de energía más bajos se muestran en la Figura\(\PageIndex{1}\). Una de las leyes fundamentales de la física es que la materia es más estable con la menor energía posible. Así, el electrón en un átomo de hidrógeno generalmente se mueve en la\(n = 1\) órbita, la órbita en la que tiene la energía más baja. Cuando el electrón se encuentra en esta órbita de menor energía, se dice que el átomo está en su estado electrónico de tierra (o simplemente estado fundamental). Si el átomo recibe energía de una fuente externa, es posible que el electrón se mueva a una órbita con un\(n\) valor mayor y el átomo se encuentra ahora en un estado electrónico excitado (o simplemente un estado excitado) con una energía superior. Cuando un electrón pasa de un estado excitado (órbita de mayor energía) a un estado menos excitado, o estado fundamental, la diferencia de energía se emite como un fotón. De igual manera, si un fotón es absorbido por un átomo, la energía del fotón mueve un electrón desde una órbita de menor energía hasta una más excitada.

alt — Figura\(\PageIndex{1}\): Números cuánticos y niveles de energía en un átomo de hidrógeno. Cuanto más negativo sea el valor calculado, menor será la energía.

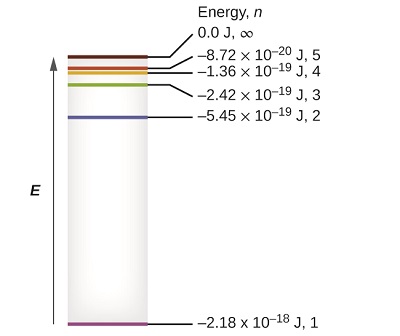
Podemos relacionar la energía de los electrones en los átomos con lo que aprendimos anteriormente sobre la energía. La ley de conservación de la energía dice que no podemos ni crear ni destruir energía. Así, si se requiere cierta cantidad de energía externa para excitar un electrón de un nivel de energía a otro, esa misma cantidad de energía se liberará cuando el electrón regrese a su estado inicial (Figura\(\PageIndex{2}\)). En efecto, un átomo puede “almacenar” energía utilizándola para promover un electrón a un estado con una mayor energía y liberarla cuando el electrón regresa a un estado inferior. La energía se puede liberar como un cuántico de energía, ya que el electrón regresa a su estado fundamental (digamos, de\(n = 5\) a\(n = 1\)), o puede liberarse como dos o más cuantos más pequeños a medida que el electrón cae a un estado intermedio, luego al estado fundamental (digamos, de\(n = 5\) a\(n = 4\), emitiendo uno quantum, luego a\(n = 1\), emitiendo un segundo quantum).

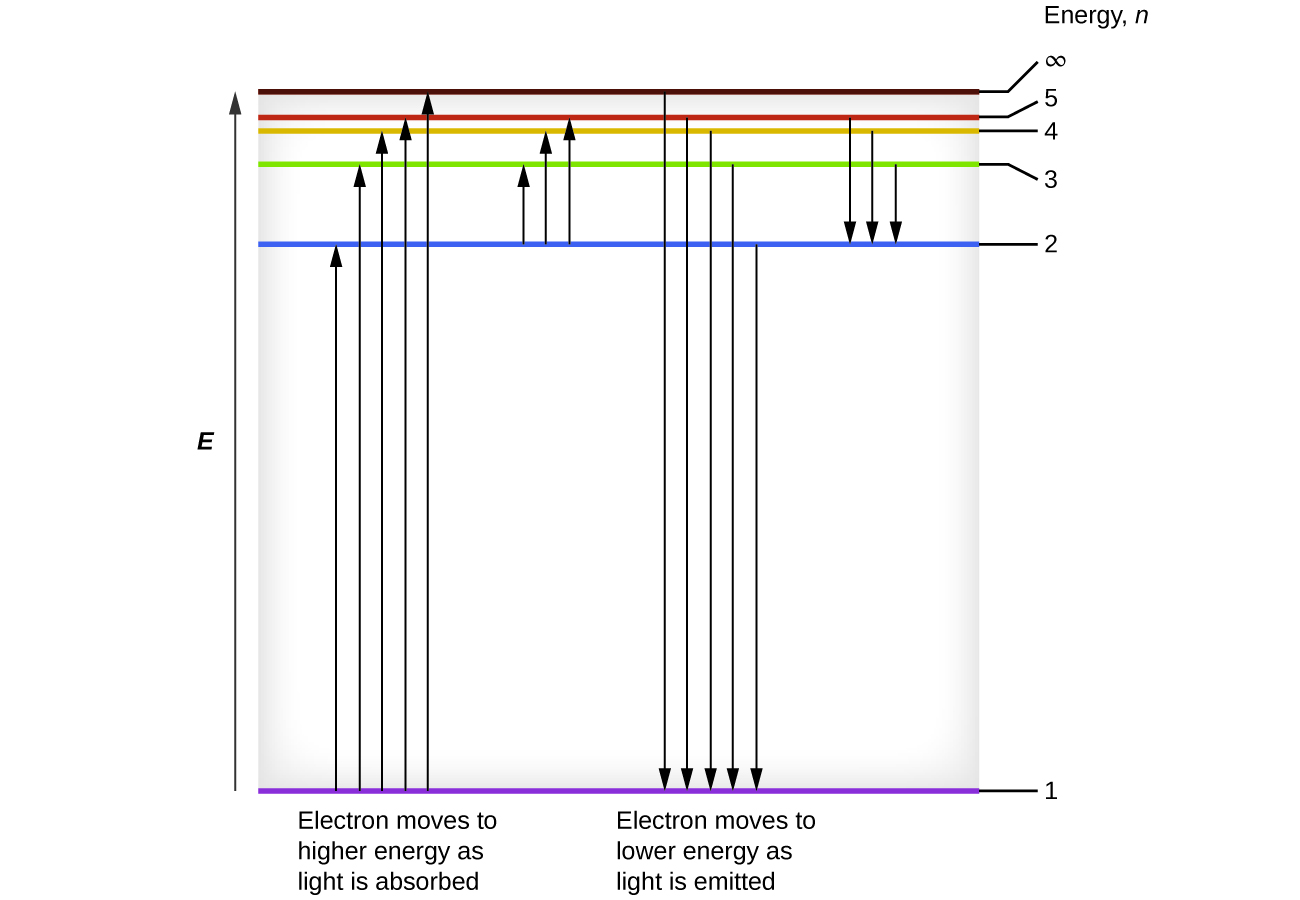
Figura\(\PageIndex{2}\): Las líneas horizontales muestran la energía relativa de las órbitas en el modelo Bohr del átomo de hidrógeno, y las flechas verticales representan la energía de los fotones absorbidos (izquierda) o emitidos (derecha) a medida que los electrones se mueven entre estas órbitas.

Dado que el modelo de Bohr implicaba solo un solo electrón, también podría aplicarse a los iones de electrones individuales He ⁺, Li ² ⁺, Be ³ ⁺, etc., que difieren del hidrógeno solo en sus cargas nucleares, y así los átomos e iones de un electrón son denominados colectivamente átomos hidrogénicos o similares a hidrógeno. La expresión de energía para átomos similares a hidrógeno es una generalización de la energía del átomo de hidrógeno, en la que\(Z\) se encuentra la carga nuclear (+1 para hidrógeno, +2 para He, +3 para Li, y así sucesivamente) y\(k\) tiene un valor de\(2.179 \times 10^{–18}\; J\).

\[ \color{red} E_n=−\dfrac{kZ^2}{n^2} \label{6.3.5} \]

Los tamaños de las órbitas circulares para los átomos similares a hidrógeno se dan en términos de sus radios mediante la siguiente expresión, en la que\(a_o\) se encuentra una constante llamada radio de Bohr, con un valor de\(5.292 \times 10^{−11}\; m\):

\[ \color{red} r=\dfrac{n^2}{Z} a_0 \label{6.3.6} \]

La ecuación también nos muestra que a medida que aumenta la energía del electrón (a medida que\(n\) aumenta), el electrón se encuentra a mayores distancias del núcleo. Esto está implícito en la dependencia inversa\(r\) en el potencial de Coulomb, ya que, a medida que el electrón se aleja del núcleo, la atracción electrostática entre éste y el núcleo disminuye, y se mantiene menos apretada en el átomo. Obsérvese que a medida que\(n\) se hace más grande y las órbitas se hacen más grandes, sus energías se acercan a cero,\(n⟶∞\) y así los límites e\(r⟶∞\) implican que\(E = 0\) corresponde al límite de ionización donde el electrón se elimina completamente del núcleo. Así, para el hidrógeno en estado fundamental\(n = 1\), la energía de ionización sería:

\[ ΔE=E_{n⟶∞} −E_1=0+k=k \label{6.3.7} \]

Con tres paradojas extremadamente desconcertantes ahora resueltas (la radiación de cuerpo negro, el efecto fotoeléctrico y el átomo de hidrógeno), y todas involucrando de manera fundamental la constante de Planck, quedó claro para la mayoría de los físicos en ese momento que las teorías clásicas que funcionaban tan bien en el mundo macroscópico eran fundamentalmente defectuoso y no podría extenderse hacia abajo en el dominio microscópico de átomos y moléculas. Desafortunadamente, a pesar del notable logro de Bohr al derivar una expresión teórica para la constante de Rydberg, no pudo extender su teoría al siguiente átomo más simple, He, que sólo tiene dos electrones. El modelo de Bohr fue severamente defectuoso, ya que aún se basaba en la noción mecánica clásica de órbitas precisas, concepto que posteriormente se encontró insostenible en el dominio microscópico, cuando se desarrolló un modelo adecuado de mecánica cuántica para reemplazarlo a la mecánica clásica.

Ejemplo\(\PageIndex{1}\): Calculating the Energy of an Electron in a Bohr Orbit

Los primeros investigadores estaban muy emocionados cuando pudieron predecir la energía de un electrón a una distancia particular del núcleo en un átomo de hidrógeno. Si una chispa promueve el electrón en un átomo de hidrógeno a una órbita con\(n = 3\), ¿cuál es la energía calculada, en julios, del electrón?

Solución

La energía del electrón viene dada por la ecuación\(\ref{6.3.5}\):

\[ E=\dfrac{−kZ^2}{n^2} \nonumber \]

El número atómico\(Z\),, de hidrógeno es 1;\(k = 2.179 \times 10^{–18}\; J\); y el electrón se caracteriza por un valor n de\(3\). Así,

\[E=\dfrac{−(2.179 \times 10^{−18}\;J)×(1)^2}{(3)^2}=−2.421 \times 10^{−19}\;J \nonumber \]

Ejercicio\(\PageIndex{1}\)

El electrón en Ejemplo\(\PageIndex{1}\) en el\(n=3\) estado se promueve aún más a una órbita con\(n = 6\). ¿Cuál es su nueva energía?

Responder: TBD

Ejemplo\(\PageIndex{2}\): Calculating Electron Transitions in a One–electron System

¿Cuál es la energía (en julios) y la longitud de onda (en metros) de la línea en el espectro de hidrógeno que representa el movimiento de un electrón desde la órbita de Bohr con n = 4 a la órbita con n = 6? ¿En qué parte del espectro electromagnético encontramos esta radiación?

Solución

En este caso, el electrón comienza con\(n = 4\), entonces\(n_1 = 4\). Viene a descansar en la\(n = 6\) órbita, entonces\(n_2 = 6\). La diferencia de energía entre los dos estados viene dada por esta expresión:

\[ΔE=E_1−E_2=2.179 \times 10^{−18}\left(\dfrac{1}{n^2_1}−\dfrac{1}{n_2^2}\right) \nonumber \]

\[ΔE=2.179 \times 10^{−18} \left(\dfrac{1}{4^2}−\dfrac{1}{6^2}\right)\; J \nonumber \]

\[ΔE=2.179 \times 10^{−18} \left(\dfrac{1}{16}−\dfrac{1}{36}\right)\;J \nonumber \]

\[ΔE=7.566 \times 10^{−20}\;J \nonumber \]

Esta diferencia de energía es positiva, lo que indica que un fotón ingresa al sistema (es absorbido) para excitar el electrón desde la órbita n = 4 hasta la\(n = 6\) órbita. La longitud de onda de un fotón con esta energía se encuentra por la expresión\(E=hc \lambda\). El reordenamiento da:

\[ \lambda=\dfrac{hc}{E} \nonumber \]

De la figura de la radiación electromagnética, podemos ver que esta longitud de onda se encuentra en la porción infrarroja del espectro electromagnético.

Ejercicio\(\PageIndex{2}\)

¿Cuál es la energía en julios y la longitud de onda en metros del fotón producida cuando un electrón cae del\(n = 5\) al\(n = 3\) nivel en un\(He^+\) ion (\(Z = 2\)para\(He^+\))?

Responder: \(6.198 \times 10^{–19}\; J\)y\(3.205 \times 10^{−7}\; m\)

El modelo de Bohr del átomo de hidrógeno proporciona información sobre el comportamiento de la materia a nivel microscópico, pero no tiene en cuenta las interacciones electrón-electrón en átomos con más de un electrón. Introduce varias características importantes de todos los modelos utilizados para describir la distribución de electrones en un átomo. Estas características incluyen las siguientes:

Se cuantifican las energías de los electrones (niveles de energía) en un átomo, descritas por números cuánticos: números enteros que tienen solo un valor específico permitido y se utilizan para caracterizar la disposición de los electrones en un átomo.
La energía de un electrón aumenta al aumentar la distancia desde el núcleo.
Las energías discretas (líneas) en los espectros de los elementos resultan de energías electrónicas cuantificadas.

De estas características, la más importante es el postulado de los niveles de energía cuantificados para un electrón en un átomo. Como consecuencia, el modelo sentó las bases para el modelo mecánico cuántico del átomo. Bohr ganó un Premio Nobel de Física por sus contribuciones a nuestra comprensión de la estructura de los átomos y cómo se relaciona con las emisiones de espectros de línea.

Resumen

Bohr incorporó las ideas de cuantificación de Planck y Einstein en un modelo del átomo de hidrógeno que resolvió la paradoja de la estabilidad atómica y los espectros discretos. El modelo Bohr del átomo de hidrógeno explica la conexión entre la cuantificación de fotones y la emisión cuantificada de átomos. Bohr describió el átomo de hidrógeno en términos de un electrón que se mueve en una órbita circular alrededor de un núcleo. Postuló que el electrón estaba restringido a ciertas órbitas caracterizadas por energías discretas. Las transiciones entre estas órbitas permitidas resultan en la absorción o emisión de fotones. Cuando un electrón se mueve de una órbita de mayor energía a una más estable, la energía se emite en forma de fotón. Para mover un electrón de una órbita estable a una más excitada, se debe absorber un fotón de energía. Usando el modelo Bohr, podemos calcular la energía de un electrón y el radio de su órbita en cualquier sistema de un electrón.

Glosario

Modelo de Bohr del átomo de hidrógeno: modelo estructural en el que un electrón se mueve alrededor del núcleo sólo en órbitas circulares, cada una con un radio permitido específico; el electrón orbitante normalmente no emite radiación electromagnética, sino que lo hace al cambiar de una órbita a otra.

estado excitado: estado que tiene una energía mayor que la energía del estado del suelo

estado de tierra: estado en el que los electrones en un átomo, ion o molécula tienen la energía más baja posible

número cuántico: número entero que tiene solo valores permitidos específicos y se utiliza para caracterizar la disposición de los electrones en un átomo