12.2: La disposición de los átomos en sólidos cristalinos
- Page ID
- 78039
- Reconocer la célula unitaria de un sólido cristalino.
- Calcular la densidad de un sólido dada su celda unitaria.
Debido a que un sólido cristalino consiste en repetir patrones de sus componentes en tres dimensiones (una celosía cristalina), podemos representar todo el cristal dibujando la estructura de las unidades idénticas más pequeñas que, cuando se apilan juntas, forman el cristal. Esta unidad repetitiva básica se llama celda unitaria. Por ejemplo, la celda unitaria de una hoja de sellos postales idénticos es un sello único, y la celda unitaria de una pila de ladrillos es un solo ladrillo. En esta sección, describimos las disposiciones de los átomos en varias celdas unitarias.
Las celdas unitarias son más fáciles de visualizar en dos dimensiones. En muchos casos, se puede usar más de una celda unitaria para representar una estructura dada, como se muestra para el dibujo de Escher en el abridor de capítulos y para una red cristalina bidimensional en la Figura 12.2. Por lo general, se elige la celda unitaria más pequeña que describe completamente el orden. El único requisito para una celda unitaria válida es que repetirla en el espacio debe producir la celosía regular. Así, la celda unitaria en la parte (d) de la Figura 12.2 no es una opción válida porque repetirla en el espacio no produce la celosía deseada (hay agujeros triangulares). El concepto de celdas unitarias se extiende a una celosía tridimensional en el dibujo esquemático de la Figura 12.3.
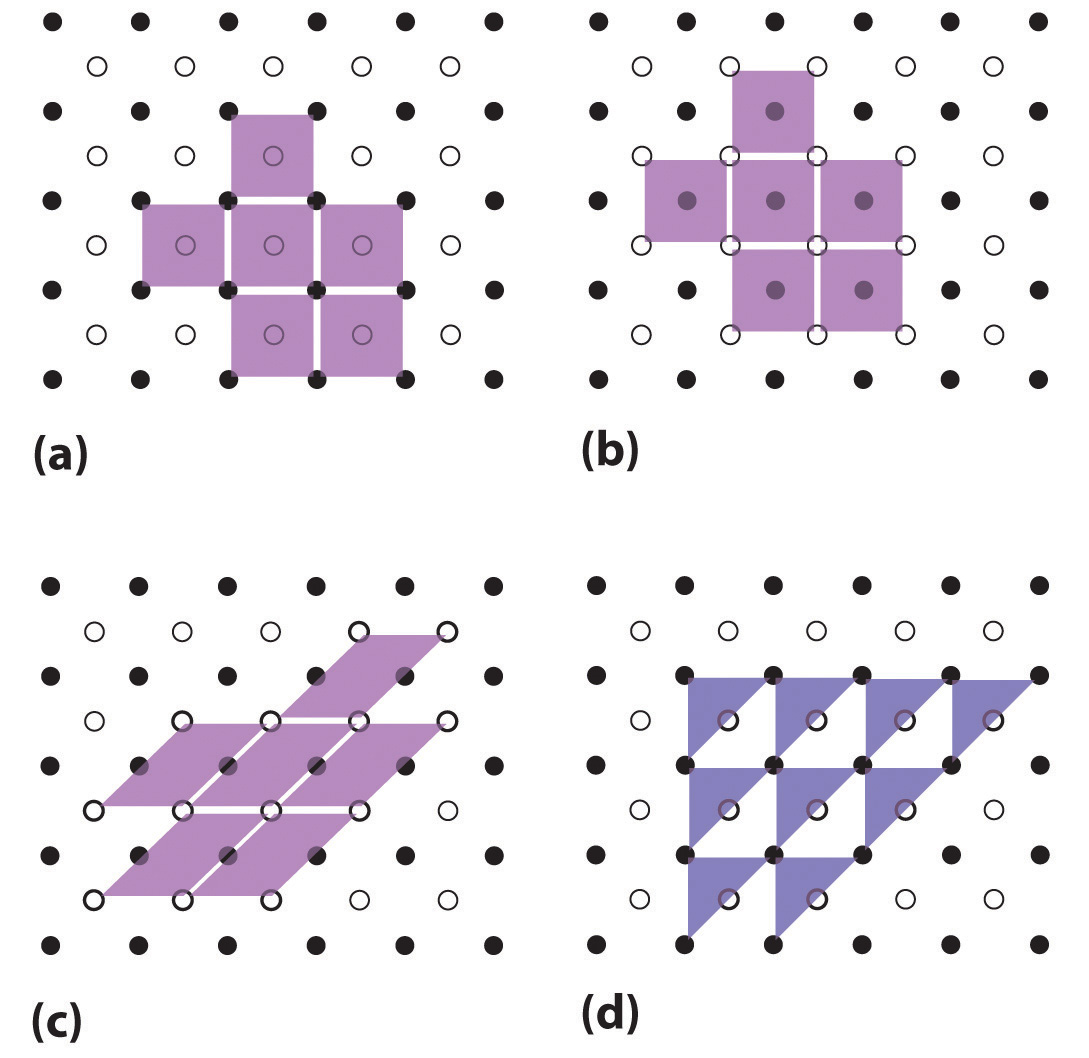
Figura 12.2 Celdas unitarias en dos dimensiones. (a—c) Tres celosías bidimensionales ilustran las posibles elecciones de la celda unitaria. Las celdas unitarias difieren en sus ubicaciones u orientaciones relativas dentro de la celosía, pero todas son opciones válidas porque repetirlas en cualquier dirección llena el patrón general de puntos. (d) El triángulo no es una celda unitaria válida porque repetirlo en el espacio llena solo la mitad del espacio en el patrón. (CC BY-NC-SA; anónimo por solicitud)

Figura 12.3 Celdas unitarias en Tres Dimensiones. Estas imágenes muestran (a) una celda unitaria tridimensional y (b) la retícula tridimensional regular resultante. (CC BY-NC-SA; anónimo por solicitud)
La celda de la unidad
Existen siete tipos fundamentalmente diferentes de celdas unitarias, que difieren en las longitudes relativas de los bordes y los ángulos entre ellos (Figura 12.4). Cada celda unitaria tiene seis lados, y cada lado es un paralelogramo. Nos enfocamos principalmente en las celdas unitarias cúbicas, en las que todos los lados tienen la misma longitud y todos los ángulos son de 90°, pero los conceptos que introducimos también se aplican a sustancias cuyas celdas unitarias no son cúbicas.

Figura 12.4 Las características generales de las siete celdas unitarias básicas. Las longitudes de los bordes de las celdas unitarias se indican con a, b y c, y los ángulos se definen de la siguiente manera: α, el ángulo entre b y c; β, el ángulo entre a y c; y γ, el ángulo entre a y b. (CC BY-NC-SA; anónimo por solicitud)
Si la celda unitaria cúbica consta de ocho átomos componentes, moléculas o iones ubicados en las esquinas del cubo, entonces se llama cúbico simple (parte (a) en la Figura 12.5). Si la celda unitaria también contiene un componente idéntico en el centro del cubo, entonces es cúbico centrado en el cuerpo (bcc) (parte (b) en la Figura 12.5). Si hay componentes en el centro de cada cara además de aquellos en las esquinas del cubo, entonces la celda unitaria es cúbica centrada en la cara (fcc) (parte (c) en la Figura 12.5).
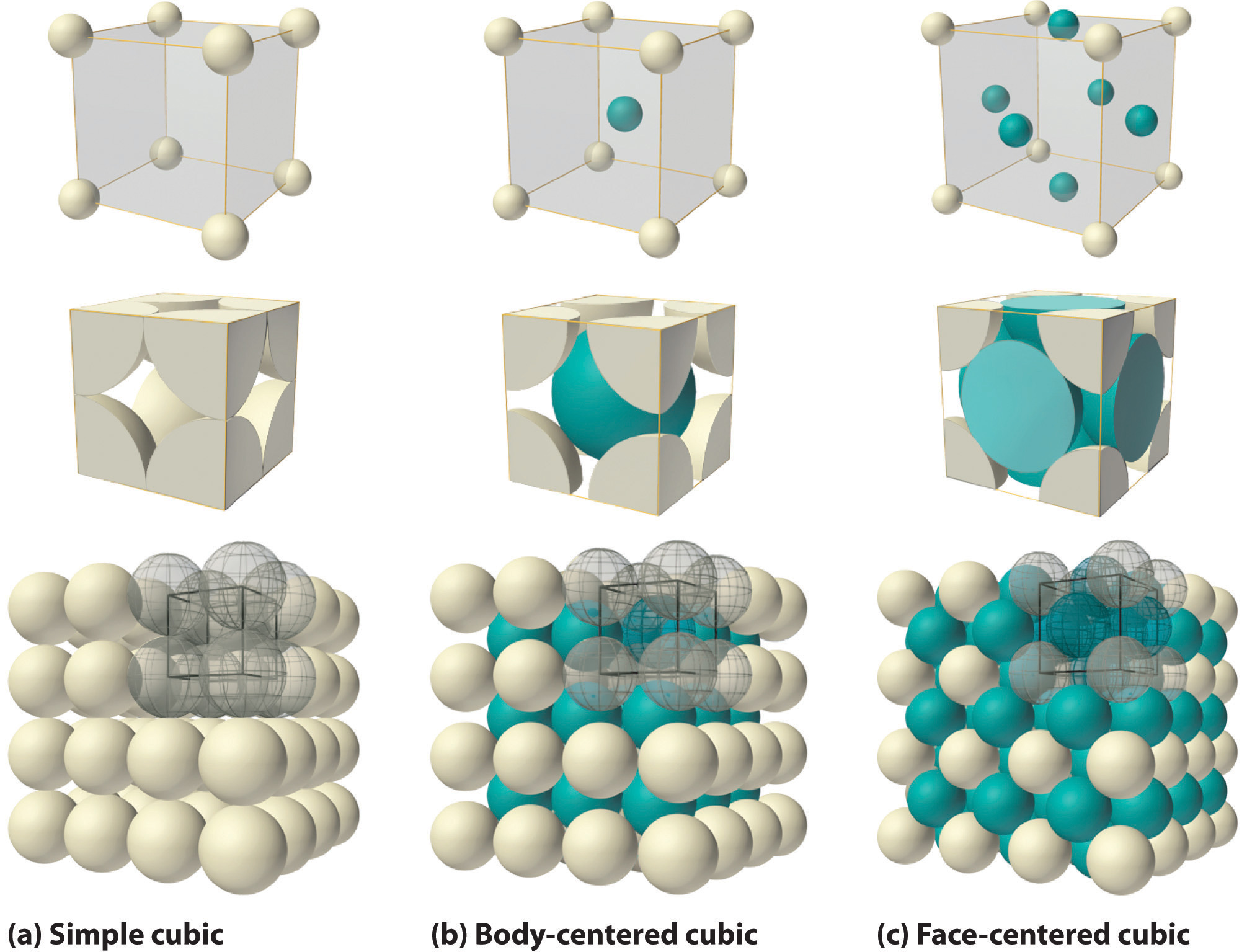
Figura 12.5 Los Tres Tipos de Celda Unitaria Cúbica. Para los tres tipos de celdas unitarias cúbicas, cúbicas simples (a), cúbicas centradas en el cuerpo (b) y cúbicas centradas en la cara (c), hay tres representaciones para cada una: un modelo de bola y palo, un modelo de corte de relleno de espacio que muestra la porción de cada átomo que se encuentra dentro de la celda unitaria, y un agregado de varios celdas unitarias. (CC BY-NC-SA; anónimo por solicitud)
Como se indica en la Figura 12.5, un sólido consiste en un gran número de celdas unitarias dispuestas en tres dimensiones. Por lo tanto, cualquier propiedad intensiva del material a granel, como su densidad, también debe estar relacionada con su celda unitaria. Debido a que la densidad es la masa de sustancia por unidad de volumen, podemos calcular la densidad del material a granel a partir de la densidad de una sola celda unitaria. Para ello, necesitamos conocer el tamaño de la celda unitaria (para obtener su volumen), la masa molar de sus componentes y el número de componentes por celda unitaria. Sin embargo, cuando contamos átomos o iones en una celda unitaria, los que se encuentran en una cara, un borde o una esquina contribuyen a más de una celda unitaria, como se muestra en la Figura 12.5. Por ejemplo, un átomo que se encuentra en una cara de una celda unitaria es compartido por dos celdas unitarias adyacentes y por lo tanto se cuenta como 12 átomos por celda unitaria. De igual manera, un átomo que se encuentra en el borde de una celda unitaria es compartido por cuatro celdas unitarias adyacentes, por lo que aporta 14 átomos a cada una. Un átomo en una esquina de una celda unitaria es compartido por las ocho celdas unitarias adyacentes y por lo tanto aporta 18 átomos a cada una. La afirmación de que los átomos que se encuentran en un borde o una esquina de una celda unitaria cuentan como 14 o 18 átomos por celda unitaria, respectivamente, es cierta para todas las celdas unitarias excepto la hexagonal, en la que tres unidades las celdas comparten cada borde vertical y seis comparten cada esquina (Figura 12.4), lo que lleva a valores de 13 y 16 átomos por celda unitaria, respectivamente, para los átomos en estas posiciones. Por el contrario, los átomos que se encuentran completamente dentro de una celda unitaria, como el átomo en el centro de una celda unitaria cúbica centrada en el cuerpo, pertenecen solo a esa celda unitaria.
| Nota |
|---|
| Para todas las celdas unitarias excepto las hexagonales, los átomos en las caras aportan\({1\over 2}\) átomo a cada celda unitaria, los átomos en los bordes aportan\({1 \over 4}\) átomo a cada celda unitaria y los átomos en las esquinas aportan\({1 \over 8}\) átomo a cada celda unitaria. |
| Ejemplo 1 |
|---|
|
El oro metálico tiene una celda unitaria cúbica centrada en la cara (parte (c) en la Figura 12.5). ¿Cuántos átomos de Au hay en cada celda unitaria? Dado: celda unitaria Preguntado por: número de átomos por celda unitaria Estrategia: Usando la Figura 12.5, identifique las posiciones de los átomos de Au en una celda unitaria cúbica centrada en la cara y luego determine cuánto contribuye cada átomo de Au a la celda unitaria. Sumar las contribuciones de todos los átomos de Au para obtener el número total de átomos de Au en una celda unitaria. Solución: Como se muestra en la Figura 12.5, una celda unitaria cúbica centrada en la cara tiene ocho átomos en las esquinas del cubo y seis átomos en las caras. Debido a que los átomos en una cara son compartidos por dos celdas unitarias, cada una cuenta como\({1 \over 2}\) átomo por celda unitaria, dando 6×\({1 \over 2}\) =3 átomos de Au por celda unitaria. Los átomos en una esquina son compartidos por ocho celdas unitarias y por lo tanto contribuyen solo\({1 \over 8}\) átomo por celda unitaria, dando 8×\({1 \over 8}\) =1 átomo de Au por celda unitaria. El número total de átomos de Au en cada celda unitaria es así de 3 + 1 = 4. |
| Ejercicio 1 |
|---|
|
El hierro metálico tiene una celda unitaria cúbica centrada en el cuerpo (parte (b) en la Figura 12.5). ¿Cuántos átomos de Fe hay en cada celda unitaria? Respuesta: two |
Ahora que sabemos contar átomos en celdas unitarias, podemos usar celdas unitarias para calcular las densidades de compuestos simples. Tenga en cuenta, sin embargo, que estamos asumiendo que un sólido consiste en una matriz regular perfecta de celdas unitarias, mientras que las sustancias reales contienen impurezas y defectos que afectan muchas de sus propiedades a granel, incluida la densidad. En consecuencia, los resultados de nuestros cálculos serán cercanos pero no necesariamente idénticos a los valores obtenidos experimentalmente.
| Ejemplo 2 |
|---|
|
Calcular la densidad del hierro metálico, que tiene una celda unitaria cúbica centrada en el cuerpo (parte (b) en la Figura 12.5) con una longitud de borde de 286.6 pm. Dado: celda unitaria y longitud de borde Preguntado por: densidad Estrategia:
Solución: A Sabemos por el Ejemplo 1 que cada celda unitaria de hierro metálico contiene dos átomos de Fe. B La masa molar de hierro es 55.85 g/mol. Debido a que la densidad es masa por unidad de volumen, necesitamos calcular la masa de los átomos de hierro en la celda unitaria a partir de la masa molar y el número de Avogadro y luego dividir la masa por el volumen de la celda (asegurándonos de usar unidades adecuadas para obtener densidad en g/cm 3): \[ mass \; of \; Fe=\left ( 2 \; \cancel{atoms} \; Fe \right )\left ( \dfrac{ 1 \; \cancel{mol}}{6.022\times 10^{23} \; \cancel{atoms}} \right )\left ( \dfrac{55.85 \; g}{\cancel{mol}} \right ) =1.855\times 10^{-22} \; g \] \[ volume=\left [ \left ( 286.6 \; pm \right )\left ( \dfrac{10^{-12 }\; \cancel{m}}{\cancel{pm}} \right )\left ( \dfrac{10^{2} \; cm}{\cancel{m}} \right ) \right ] =2.345\times 10^{-23} \; cm^{3} \] \[ density = \dfrac{1.855\times 10^{-22} \; g}{2.345\times 10^{-23} \; cm^{3}} = 7.880 g/cm^{3} \] Este resultado se compara bien con el valor experimental tabulado de 7.874 g/cm 3. |
| Ejercicio |
|---|
|
Calcular la densidad del oro, que tiene una celda unitaria cúbica centrada en la cara (parte (c) en la Figura 12.5) con una longitud de borde de 407.8 pm. Respuesta: 19.29 g/cm 3 |
Empaque de Esferas
Nuestra discusión sobre las estructuras tridimensionales de los sólidos ha considerado únicamente sustancias en las que todos los componentes son idénticos. Como veremos, tales sustancias pueden verse como consistentes en esferas idénticas empaquetadas juntas en el espacio; la forma en que los componentes se empaquetan produce las diferentes celdas unitarias. La mayoría de las sustancias con estructuras de este tipo son metales.
Estructura cúbica simple
La disposición de los átomos en un sólido que tiene una celda unitaria cúbica simple se mostró en la parte (a) en la Figura 12.5. Cada átomo en la celosía tiene sólo seis vecinos más cercanos en una disposición octaédrica. En consecuencia, la simple celosía cúbica es una forma ineficiente de empaquetar átomos juntos en el espacio: solo 52% del espacio total es llenado por los átomos. El único elemento que cristaliza en una celda unitaria cúbica simple es el polonio. Las celdas unitarias cúbicas simples son, sin embargo, comunes entre los compuestos iónicos binarios, donde cada catión está rodeado por seis aniones y viceversa.
La disposición de los átomos en una celda unitaria cúbica simple. Cada átomo en la red tiene seis vecinos más cercanos en una disposición octaédrica.
Estructura cúbica centrada en el cuerpo
La celda unitaria cúbica centrada en el cuerpo es una forma más eficiente de empaquetar esferas y es mucho más común entre los elementos puros. Cada átomo tiene ocho vecinos más cercanos en la celda unitaria, y 68% del volumen está ocupado por los átomos. Como se muestra en la parte (b) de la Figura 12.5, la estructura cúbica centrada en el cuerpo consiste en una sola capa de esferas en contacto entre sí y alineadas de manera que sus centros están en las esquinas de un cuadrado; una segunda capa de esferas ocupa los “agujeros” de forma cuadrada por encima de las esferas en la primera capa. La tercera capa de esferas ocupa los agujeros cuadrados formados por la segunda capa, de manera que cada una se encuentra directamente sobre una esfera en la primera capa, y así sucesivamente. Todos los metales alcalinos, bario, radio y varios de los metales de transición tienen estructuras cúbicas centradas en el cuerpo.
Estructuras hexagonales empaquetadas y cúbicas compactas
La forma más eficiente de empacar esferas es el arreglo compacto, que tiene dos variantes. Una sola capa de esferas compactas se muestra en la parte (a) en la Figura 12.6. Cada esfera está rodeada por otras seis en el mismo plano para producir una disposición hexagonal. Por encima de cualquier conjunto de siete esferas hay seis depresiones dispuestas en un hexágono. En principio, los seis sitios son iguales, y cualquiera de ellos podría estar ocupado por un átomo en la siguiente capa. En realidad, sin embargo, estos seis sitios pueden dividirse en dos conjuntos, etiquetados B y C en la parte (a) en la Figura 12.6. Los sitios B y C difieren porque tan pronto como colocamos una esfera en una posición B, ya no podemos colocar una esfera en ninguna de las tres posiciones C adyacentes a A y viceversa.

Figura 12.6: Capas de Esferas Empaquetadas Cerradas. (a) En esta sola capa de esferas muy compactas, cada esfera está rodeada por otras seis en una disposición hexagonal. (b) Colocar un átomo en una posición B prohíbe colocar un átomo en cualquiera de las posiciones C adyacentes y da como resultado que todos los átomos de la segunda capa ocupen las posiciones B. (c) Colocar los átomos en la tercera capa sobre los átomos en las posiciones A en la primera capa da la estructura hexagonal compacta. Colocar los átomos de la tercera capa sobre las posiciones C da la estructura cúbica muy compacta. (CC BY-NC-SA; anónimo por solicitud)
Si colocamos la segunda capa de esferas en las posiciones B en la parte (a) de la Figura 12.6, obtenemos la estructura de dos capas que se muestra en la parte (b) en la Figura 12.6. Ahora existen dos alternativas para colocar el primer átomo de la tercera capa: podemos colocarlo directamente sobre uno de los átomos en la primera capa (una posición A) o en una de las posiciones C, correspondientes a las posiciones que no usamos para los átomos en la primera o segunda capa (parte (c) en la Figura 12.6). Si elegimos la primera disposición y repetimos el patrón en capas sucesivas, las posiciones de los átomos se alternan de capa a capa en el patrón ABABAB..., dando como resultado una estructura hexagonal empaquetada (hcp) (parte (a) en la Figura 12.7). Si elegimos la segunda disposición y repetimos el patrón indefinidamente, las posiciones de los átomos se alternan como ABCABC..., dando una estructura cúbica empaquetada (ccp) (parte (b) en la Figura 12.7). Debido a que la estructura ccp contiene capas empaquetadas hexagonalmente, no se ve particularmente cúbica. Como se muestra en la parte (b) de la Figura 12.7, sin embargo, el simple giro de la estructura revela su naturaleza cúbica, la cual es idéntica a una estructura fcc. Las estructuras hcp y ccp difieren solo en la forma en que se apilan sus capas. Ambas estructuras tienen una eficiencia global de empaque de 74%, y en ambas cada átomo tiene 12 vecinos más cercanos (6 en el mismo plano más 3 en cada uno de los planos inmediatamente arriba y abajo).

Figura 12.7 Estructuras Close-Packed: hcp y ccp. Las ilustraciones de (a) muestran una vista despiezada, una vista lateral y una vista superior de la estructura hcp. La celda unitaria hexagonal simple se describe en las vistas lateral y superior. Obsérvese la similitud con la celda unitaria hexagonal mostrada en la Figura 12.4. La estructura ccp en (b) se muestra en una vista despiezada, una vista lateral y una vista girada. La vista girada enfatiza la naturaleza fcc de la celda unitaria (delineada). La línea que conecta los átomos en la primera y cuarta capas de la estructura ccp es la diagonal del cuerpo del cubo. (CC BY-NC-SA; anónimo por solicitud)
En el Cuadro 12.1 se compara la eficiencia de empaque y el número de vecinos más cercanos para las diferentes estructuras cúbicas y compactas; el número de vecinos más cercanos se denomina número de coordinación. La mayoría de los metales tienen estructuras hcp, ccp o bcc, aunque varios metales presentan estructuras tanto hcp como ccp, dependiendo de la temperatura y la presión.
Cuadro 12.1: Propiedades de las Estructuras Comunes de los Metales
| Estructura | Porcentaje del Espacio Ocupado por Átomos | Número de Coordinación |
|---|---|---|
| cúbico simple | 52 | 6 |
| cúbico centrado en el cuerpo | 68 | 8 |
| hexagonal, cierre, embalado | 74 | 12 |
| cúbico empaquetado cerrado (idéntico al cúbico centrado en la cara) | 74 | 12 |
Resumen
La unidad repetitiva más pequeña de una red cristalina es la celda unitaria. La celda unitaria cúbica simple contiene solo ocho átomos, moléculas o iones en las esquinas de un cubo. Una celda unitaria cúbica centrada en el cuerpo (bcc) contiene un componente adicional en el centro del cubo. Una celda unitaria cúbica centrada en la cara (fcc) contiene un componente en el centro de cada cara además de aquellos en las esquinas del cubo. Los arreglos simples cúbicos y bcc llenan solo 52% y 68% del espacio disponible con átomos, respectivamente. La estructura hexagonal cerrada (hcp) tiene un ABABAB... disposición repetitiva, y la estructura cúbica cerrada (ccp) tiene un patrón repetitivo ABCABC...; este último es idéntico a una celosía fcc. Los arreglos hcp y ccp llenan 74% del espacio disponible y tienen un número de coordinación de 12 por cada átomo en la celosía, el número de vecinos más cercanos. Las celosías cúbicas simples y bcc tienen números de coordinación de 6 y 8, respectivamente.
Llave para llevar
Un sólido cristalino puede ser representado por su celda unitaria, que es la unidad idéntica más pequeña que cuando se apilan juntas produce la estructura tridimensional característica.
Problemas conceptuales
1. ¿Por qué es válido representar la estructura de un sólido cristalino por la estructura de su celda unitaria? ¿Cuáles son las restricciones más importantes en la selección de una celda unitaria?
2. Todas las estructuras de celdas unitarias tienen seis lados. ¿Pueden los cristales de un sólido tener más de seis lados? Explica tu respuesta.
3. Explicar cómo se reflejan las propiedades intensivas de un material en la celda unitaria. ¿Todas las propiedades de un material a granel son las mismas que las de su celda unitaria? Explica tu respuesta.
4. La densidad medida experimentalmente de un material a granel es ligeramente superior a lo esperado en base a la estructura del material puro. Proponer dos explicaciones para esta observación.
5. La densidad determinada experimentalmente de un material es menor de lo esperado en función de la disposición de los átomos en la celda unitaria, la masa de la fórmula y el tamaño de los átomos. ¿Qué conclusión (es) puedes sacar sobre el material?
6. Solo un elemento (polonio) cristaliza con una simple celda unitaria cúbica. ¿Por qué el polonio es el único ejemplo de un elemento con esta estructura?
7. ¿Qué se entiende por el término número de coordinación en la estructura de un sólido? ¿Cómo depende el número de coordinación de la estructura del metal?
8. Organice los tres tipos de celdas unitarias cúbicas para aumentar la eficiencia de empaque. ¿Cuál es la diferencia en la eficiencia de empaque entre la estructura hcp y la estructura ccp?
9. Las estructuras de muchos metales dependen de la presión y la temperatura. ¿Qué estructura, bcc o hcp, sería más probable en un metal dado a presiones muy altas? Explica tu razonamiento.
10. Un metal tiene dos fases cristalinas. La temperatura de transición, la temperatura a la que una fase se convierte a la otra, es de 95°C a 1 atm y 135°C a 1000 atm. Esboce un diagrama de fases para esta sustancia. Se sabe que el metal tiene una estructura ccp o una estructura cúbica simple. Etiquete adecuadamente las regiones en su diagrama y justifique su selección para la estructura de cada fase.
Problemas numéricos
1. El rodio metálico tiene una celda unitaria fcc. ¿Cuántos átomos de rodio contiene cada celda unitaria?
2. El cromo tiene una estructura con dos átomos por celda unitaria. ¿La estructura de este metal es simple cúbica, bcc, fcc o hcp?
3. La densidad del níquel es de 8.908 g/cm 3. Si el radio metálico del níquel es de 125pm, ¿cuál es la estructura del níquel metálico?
4. La densidad del tungsteno es de 19.3 g/cm 3. Si el radio metálico del tungsteno es de 139pm, ¿cuál es la estructura del tungsteno metálico?
5. Un elemento tiene una densidad de 10.25 g/cm 3 y un radio metálico de 136.3 pm. El metal cristaliza en una celosía bcc. Identificar el elemento.
6. Una muestra de 21.64 g de un metal no reactivo se coloca en un matraz que contiene 12.00 mL de agua; el volumen final es 13.81 mL. Si la longitud del borde de la celda unitaria es 387pm y el radio metálico es 137pm, determine la disposición de empaque e identifique el elemento.
7. Se encontró que una muestra de un metal alcalino que tiene una celda unitaria bcc tiene una masa de 1.000 g y un volumen de 1.0298 cm 3. Cuando el metal reacciona con exceso de agua, la reacción produce 539.29 mL de gas hidrógeno a 0.980 atm y 23°C. Identificar el metal, determinar las dimensiones de la celda unitaria y dar el tamaño aproximado del átomo en picometros.
8. Se encontró que una muestra de un metal alcalinotérreo que tiene una celda unitaria bcc tiene una masa de 5.000 g y un volumen de 1.392 cm 3. La reacción completa con gas cloro requiere 848.3 mL de gas cloro a 1.050 atm y 25°C. Identificar el metal, determinar las dimensiones de la celda unitaria y dar el tamaño aproximado del átomo en picometros.
9. El litio cristaliza en una estructura bcc con una longitud de borde de 3.509 Å. Calcular su densidad. ¿Cuál es el radio metálico aproximado del litio en picometros?
10. El vanadio se utiliza en la fabricación de acero al vanadio resistente a la corrosión. Forma cristales bcc con una densidad de 6.11 g/cm 3 a 18.7°C ¿Cuál es la longitud del borde de la celda unitaria? ¿Cuál es el radio metálico aproximado del vanadio en picometros?
11. Una celda cúbica simple contiene un átomo de metal con un radio metálico de 100pm.
a. Determinar el volumen del átomo o átomos contenidos en una celda unitaria [el volumen de una esfera = (\({4 \over 3} \)) πr 3].
b. ¿Cuál es la longitud de un borde de la celda unitaria? (Pista: no hay espacio vacío entre los átomos.)
c. Calcular el volumen de la celda unitaria.
d. Determinar la eficiencia de empaque para esta estructura.
e. Utilice los pasos del Problema 11 para calcular la eficiencia de empaque para una celda unitaria bcc con un radio metálico de 1.00 Å.
Respuestas numéricas
1. cuatro
3. fcc
5. molibdeno
7. sodio, borde de celda unitaria = 428pm, r = 185pm
9. d = 0.5335 g/cm 3, r =151.9 pm



