11.4: Propiedades coligativas
- Page ID
- 75325
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Concentraciones expresas de componentes de la solución usando fracción molar y molalidad
- Describir el efecto de la concentración de soluto sobre diversas propiedades de la solución (presión de vapor, punto de ebullición, punto de congelación y presión osmótica)
- Realizar cálculos utilizando las ecuaciones matemáticas que describen estos diversos efectos colligativos
- Describir el proceso de destilación y sus aplicaciones prácticas
- Explicar el proceso de ósmosis y describir cómo se aplica industrialmente y en la naturaleza
Las propiedades de una solución son diferentes de las del soluto (s) puro (s) o disolvente (s). Muchas propiedades de la solución dependen de la identidad química del soluto. En comparación con el agua pura, una solución de cloruro de hidrógeno es más ácida, una solución de amoníaco es más básica, una solución de cloruro de sodio es más densa y una solución de sacarosa es más viscosa. Existen algunas propiedades de solución, sin embargo, que dependen únicamente de la concentración total de especies de solutos, independientemente de sus identidades. Estas propiedades coligativas incluyen la disminución de la presión de vapor, la elevación del punto de ebullición, la depresión del punto de congelación y la presión osmótica. Este pequeño conjunto de propiedades es de importancia central para muchos fenómenos naturales y aplicaciones tecnológicas, como se describirá en este módulo.
Fracción molar y Molalidad
Varias unidades de uso común para expresar las concentraciones de componentes de la solución se introdujeron en un capítulo anterior de este texto, cada una de las cuales proporciona ciertos beneficios para su uso en diferentes aplicaciones. Por ejemplo, la molaridad (M) es una unidad conveniente para su uso en cálculos estequiométricos, ya que se define en términos de las cantidades molares de especies de solutos:
\[M=\dfrac{\text{mol solute}}{\text{L solution}} \label{11.5.1} \]
Debido a que los volúmenes de solución varían con la temperatura, las concentraciones molares también variarán Cuando se expresa como molaridad, la concentración de una solución con números idénticos de especies de soluto y disolvente será diferente a diferentes temperaturas, debido a la contracción/expansión de la solución. Más apropiadas para los cálculos que involucran muchas propiedades coligativas son las unidades de concentración basadas en moles cuyos valores no dependen de la temperatura. Dos de estas unidades son la fracción molar (introducida en el capítulo anterior sobre gases) y la molalidad.
La fracción molar,\(\chi\), de un componente es la relación de su cantidad molar al número total de moles de todos los componentes de la solución:
\[\chi_\ce{A}=\dfrac{\text{mol A}}{\text{total mol of all components}} \label{11.5.2} \]
La molalidad es una unidad de concentración definida como la relación de los números de moles de soluto a la masa del disolvente en kilogramos:
\[m=\dfrac{\text{mol solute}}{\text{kg solvent}} \label{11.5.3} \]
Dado que estas unidades se calculan utilizando únicamente masas y cantidades molares, no varían con la temperatura y, por lo tanto, son más adecuadas para aplicaciones que requieren concentraciones independientes de la temperatura, incluyendo varias propiedades coligativas, como se describirá en este módulo de capítulo.
El anticongelante en la mayoría de los radiadores de automóviles es una mezcla de volúmenes iguales de etilenglicol y agua, con cantidades menores de otros aditivos que evitan la corrosión. ¿Cuáles son las (a) fracción molar y (b) molalidad del etilenglicol, C 2 H 4 (OH) 2, en una solución preparada a partir\(\mathrm{2.22 \times 10^3 \;g}\) de etilenglicol y\(\mathrm{2.00 \times 10^3\; g}\) de agua (aproximadamente 2 L de glicol y 2 L de agua)?
Solución
(a) La fracción molar de etilenglicol puede calcularse derivando primero cantidades molares de ambos componentes de la solución y luego sustituyendo estas cantidades en la definición de unidad.
\(\mathrm{mol\:H_2O=2000\:g×\dfrac{1\:mol\:H_2O}{18.02\:g\:H_2O}=111\:mol\:H_2O}\)
\(\chi_\mathrm{ethylene\:glycol}=\mathrm{\dfrac{35.8\:mol\:C_2H_4(OH)_2}{(35.8+111)\:mol\: total}=0.245}\)
Observe que la fracción molar es una propiedad adimensional, siendo la relación de propiedades con unidades idénticas (moles).
(b) Para encontrar molalidad, necesitamos conocer los moles del soluto y la masa del disolvente (en kg).
Primero, use la masa dada de etilenglicol y su masa molar para encontrar los moles de soluto:
\[\mathrm{2220\:g\:C_2H_4(OH)_2\left(\dfrac{mol\:C_2H_2(OH)_2}{62.07\:g}\right)=35.8\:mol\:C_2H_4(OH)_2} \nonumber \]
Después, convertir la masa del agua de gramos a kilogramos:
\[\mathrm{2000\: g\:H_2O\left(\dfrac{1\:kg}{1000\:g}\right)=2\: kg\:H_2O} \nonumber \]
Finalmente, calcula la molaridad según su definición:
\ [\ begin {alinear*}
\ ce {molalidad} &=\ mathrm {\ dfrac {mol\: soluto} {kg\: solvente}}\\
\ ce {molalidad} &=\ mathrm {\ dfrac {35.8\ :mol\ :C_2H_4 (OH) _2} {2\ :kg\ :H_2O}}\\
\ ce {molalidad} &=17.9\ :m
\ end {align*}\ nonumber\]
¿Cuáles son la fracción molar y molalidad de una solución que contiene 0.850 g de amoníaco, NH 3, disueltos en 125 g de agua?
- Contestar
-
7.14 × 10 −3; 0.399 m
Calcular la fracción molar de soluto y disolvente en una solución de 3.0 m de cloruro de sodio.
Sol ución
La conversión de una unidad de concentración a otra se logra comparando primero las dos definiciones de unidades. En este caso, ambas unidades tienen el mismo numerador (moles de soluto) pero diferentes denominadores. La concentración molal proporcionada puede escribirse como:
\[\mathrm{\dfrac{3.0\;mol\; NaCl}{1.0\; kg\; H_2O}} \nonumber \]
El numerador para la fracción molar de esta solución es, por lo tanto, 3.0 mol de NaCl. El denominador puede calcularse derivando la cantidad molar de agua correspondiente a 1.0 kg
\[\mathrm{1.0\:kg\:H_2O\left(\dfrac{1000\:g}{1\:kg}\right)\left(\dfrac{mol\:H_2O}{18.02\:g}\right)=55\:mol\:H_2O} \nonumber \]
y luego sustituir estas cantidades molares en la definición de fracción molar.
\ [\ begin {alinear*}
X_\ mathrm {H_2O} &=\ mathrm {\ dfrac {mol\ :H_2O} {mol\: NaCl + mol\ :H_2O}}\\
X_\ mathrm {H_2O} &=\ mathrm {\ dfrac {55\ :mol\ :H_2O} {3.0\ :mol\: NaCl+55\ :mol\ :H_2O}}\\
X_\ mathrm {H_2O} &=0.95\\
X_\ mathrm {NaCl} &=\ mathrm {\ dfrac {mol\: NaCl} { mol\: NaCl+mol\ :H_2O}}\\
X_\ mathrm {NaCl} &=\ mathrm {\ dfrac {3.0\ :mol\ :NaCl} {3.0\ :mol\: NaCl+55\ :mol\ :H_2O}}\\
X_\ mathrm {NaCl} &=0.052
\ final {alinear*}\ nonumber\]
La fracción molar de yodo\(\ce{I_2}\), disuelta en diclorometano\(\ce{CH_2Cl_2}\), es de 0.115. ¿Cuál es la concentración molal, m, de yodo en esta solución?
- Contestar
-
1.50 m
Bajar la presión de vapor
Como se describe en el capítulo sobre líquidos y sólidos, la presión de vapor de equilibrio de un líquido es la presión ejercida por su fase gaseosa cuando se producen vaporización y condensación a tasas iguales:
\[ \text{liquid} \rightleftharpoons \text{gas} \label{11.5.4} \]
Disolver una sustancia no volátil en un líquido volátil resulta en una disminución de la presión de vapor del líquido. Este fenómeno se puede racionalizar considerando el efecto de las moléculas de soluto añadidas en los procesos de vaporización y condensación del líquido. Para vaporizar, las moléculas de disolvente deben estar presentes en la superficie de la solución. La presencia de soluto disminuye la superficie disponible para las moléculas de disolvente y, por lo tanto, reduce la velocidad de vaporización del disolvente. Dado que la velocidad de condensación no se ve afectada por la presencia de soluto, el resultado neto es que el equilibrio de vaporización-condensación se logra con menos moléculas de disolvente en la fase de vapor (es decir, a una presión de vapor más baja) (Figura\(\PageIndex{1}\)). Si bien esta interpretación cinética es útil, no tiene en cuenta varios aspectos importantes de la naturaleza coligativa de la disminución de la presión de vapor. Una explicación más rigurosa involucra la propiedad de la entropía, tema de discusión en un capítulo posterior de texto sobre termodinámica. Para los fines de entender la disminución de la presión de vapor de un líquido, es adecuado señalar que la mayor entropía de una solución en comparación con su disolvente y soluto separados sirve para estabilizar eficazmente las moléculas de disolvente y obstaculizar su vaporización. Se obtiene una presión de vapor más baja y un punto de ebullición correspondientemente mayor como se describe en la siguiente sección de este módulo.
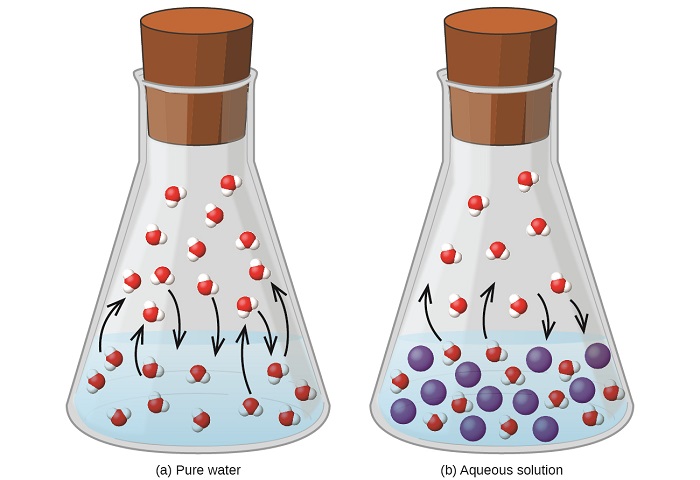
La relación entre las presiones de vapor de los componentes de la solución y las concentraciones de esos componentes se describe por la ley de Raoult: La presión parcial ejercida por cualquier componente de una solución ideal es igual a la presión de vapor del componente puro multiplicada por su mol fracción en la solución.
\[P_\ce{A}=X_\ce{A}P^\circ_\ce{A} \label{11.5.5} \]
donde P A es la presión parcial ejercida por el componente A en la solución,\(P^\circ_\ce{A}\) es la presión de vapor de A pura, y X A es la fracción molar de A en la solución. (La fracción molar es una unidad de concentración introducida en el capítulo sobre gases.)
Recordando que la presión total de una mezcla gaseosa es igual a la suma de presiones parciales para todos sus componentes (ley de Dalton de presiones parciales), la presión de vapor total ejercida por una solución que contiene i componentes es
\[P_\ce{solution}=\sum_{i}P_i=\sum_{i}X_iP^\circ_i \label{11.5.6} \]
Una sustancia no volátil es aquella cuya presión de vapor es despreciable (P° ≈ 0), por lo que la presión de vapor por encima de una solución que contiene solo solutos no volátiles se debe únicamente al disolvente:
\[P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent} \label{11.5.7} \]
Calcular la presión de vapor de una solución ideal que contiene 92.1 g de glicerina, C 3 H 5 (OH) 3, y 184.4 g de etanol, C 2 H 5 OH, a 40 °C. La presión de vapor del etanol puro es de 0.178 atm a 40 °C. La glicerina es esencialmente no volátil en este temperatura.
Solución
Dado que el disolvente es el único componente volátil de esta solución, su presión de vapor puede calcularse según la ley de Raoult como:
\(P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent}\)
Primero, calcule las cantidades molares de cada componente de la solución utilizando los datos de masa proporcionados.
\(\mathrm{92.1\cancel{g\:C_3H_5(OH)_3}×\dfrac{1\:mol\:C_3H_5(OH)_3}{92.094\cancel{g\:C_3H_5(OH)_3}}=1.00\:mol\:C_3H_5(OH)_3}\)
A continuación, calcule la fracción molar del disolvente (etanol) y use la ley de Raoult para calcular la presión de vapor de la solución.
\(X_\mathrm{C_2H_5OH}=\mathrm{\dfrac{4.000\:mol}{(1.00\:mol+4.000\:mol)}=0.800}\)
\(P_\ce{solv}=X_\ce{solv}P^\circ_\ce{solv}=\mathrm{0.800×0.178\:atm=0.142\:atm}\)
Una solución contiene 5.00 g de urea, CO (NH 2) 2 (un soluto no volátil) y 0.100 kg de agua. Si la presión de vapor del agua pura a 25 °C es de 23.7 torr, ¿cuál es la presión de vapor de la solución?
- Contestar
-
23,4 torr
Elevación del Punto de Ebullición de un Solvente
Como se describe en el capítulo sobre líquidos y sólidos, el punto de ebullición de un líquido es la temperatura a la que su presión de vapor es igual a la presión atmosférica ambiente. Dado que la presión de vapor de una solución disminuye debido a la presencia de solutos no volátiles, es lógico pensar que posteriormente se incrementará el punto de ebullición de la solución. En comparación con el solvente puro, una solución, por lo tanto, requerirá una temperatura más alta para lograr cualquier presión de vapor dada, incluyendo una equivalente a la de la atmósfera circundante. El incremento en el punto de ebullición observado cuando el soluto no volátil se disuelve en un disolvente\(ΔT_b\), se denomina elevación del punto de ebullición y es directamente proporcional a la concentración molal de las especies de solutos:
\[ΔT_b=K_bm \label{11.5.8} \]
donde
- \(K_\ce{b}\)es la constante de elevación del punto de ebullición, o la constante ebuloscópica y
- \(m\)es la concentración molal (molalidad) de todas las especies de solutos.
Las constantes de elevación del punto de ebullición son propiedades características que dependen de la identidad del disolvente. Los valores de K b para varios solventes se listan en la Tabla\(\PageIndex{1}\).
| Solvente | Punto de ebullición (°C a 1 atm) | K b (Cm −1) | Punto de congelación (°C a 1 atm) | K f (Cm −1) |
|---|---|---|---|---|
| agua | 100.0 | 0.512 | 0.0 | 1.86 |
| acetato de hidrógeno | 118.1 | 3.07 | 16.6 | 3.9 |
| benceno | 80.1 | 2.53 | 5.5 | 5.12 |
| cloroformo | 61.26 | 3.63 | −63.5 | 4.68 |
| nitrobenceno | 210.9 | 5.24 | 5.67 | 8.1 |
El grado en que se disminuye la presión de vapor de un disolvente y se eleva el punto de ebullición depende del número total de partículas de soluto presentes en una cantidad dada de disolvente, no de la masa o tamaño o identidades químicas de las partículas. Una solución acuosa de sacarosa de 1 m (342 g/mol) y una solución acuosa de etilenglicol de 1 m (62 g/mol) exhibirán el mismo punto de ebullición porque cada solución tiene un mol de partículas de soluto (moléculas) por kilogramo de disolvente.
¿Cuál es el punto de ebullición de una solución de 0.33 m de un soluto no volátil en benceno?
Solución
Utilice la ecuación que relaciona la elevación del punto de ebullición con la molalidad del soluto para resolver este problema en dos pasos.

- Calcular el cambio en el punto de ebullición.
\(ΔT_\ce{b}=K_\ce{b}m=2.53\:°\ce C\:m^{−1}×0.33\:m=0.83\:°\ce C\)
- Añadir la elevación del punto de ebullición al punto de ebullición del disolvente puro.
\(\mathrm{Boiling\: temperature=80.1\:°C+0.83\:°C=80.9\:°C}\)
¿Cuál es el punto de ebullición del anticongelante descrito en Ejemplo\(\PageIndex{4}\)?
- Contestar
-
109.2 °C
Encontrar el punto de ebullición de una solución de 92.1 g de yodo,\(\ce{I2}\), en 800.0 g de cloroformo,\(\ce{CHCl3}\), asumiendo que el yodo es no volátil y que la solución es ideal.
Solución
Podemos resolver este problema usando cuatro pasos.

- Convertir de gramos a moles de\(\ce{I2}\) usando la masa molar de\(\ce{I2}\) en el factor de conversión unitario.
Resultado: 0.363 mol
Determinar la molalidad de la solución a partir del número de moles de soluto y la masa de disolvente, en kilogramos.
Resultado: 0.454 m
Utilice la proporcionalidad directa entre el cambio en el punto de ebullición y la concentración de molal para determinar cuánto cambia el punto de ebullición.
Resultado: 1.65 °C
Determinar el nuevo punto de ebullición a partir del punto de ebullición del disolvente puro y el cambio.
Resultado: 62.91 °C
Verificar cada resultado como una autoevaluación.
¿Cuál es el punto de ebullición de una solución de 1.0 g de glicerina\(\ce{C3H5(OH)3}\),, en 47.8 g de agua? Asumir una solución ideal.
- Contestar
-
100.12 °C
Destilación de Soluciones
La destilación es una técnica para separar los componentes de mezclas que se aplica ampliamente tanto en el laboratorio como en entornos industriales. Se utiliza para refinar petróleo, aislar productos de fermentación y purificar el agua. Esta técnica de separación implica el calentamiento controlado de una mezcla de muestra para vaporizar, condensar y recolectar selectivamente uno o más componentes de interés. Un aparato típico para destilaciones a escala de laboratorio se muestra en la Figura\(\PageIndex{2}\).
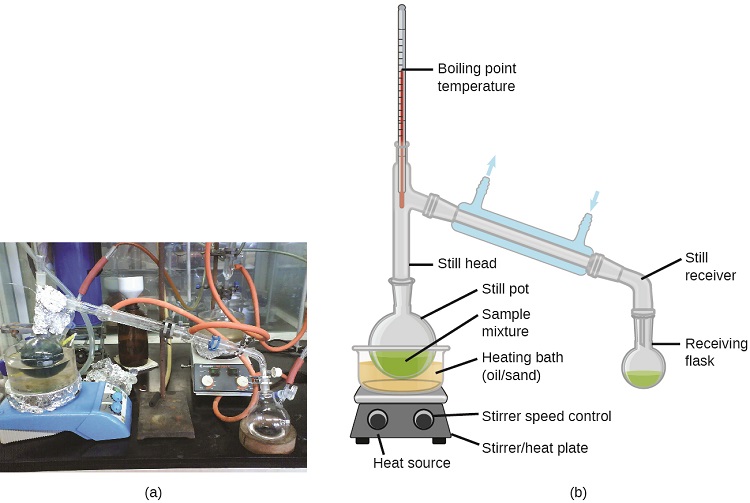
Las refinerías de petróleo utilizan destilación fraccionada a gran escala para separar los componentes del petróleo crudo. El petróleo crudo se calienta a altas temperaturas en la base de una columna de fraccionamiento alto, vaporizando muchos de los componentes que se elevan dentro de la columna. A medida que los componentes vaporizados alcanzan zonas adecuadamente frías durante su ascenso, se condensan y se recolectan. Los líquidos recolectados son mezclas más simples de hidrocarburos y otros compuestos del petróleo que son de composición apropiada para diversas aplicaciones (por ejemplo, combustible diesel, queroseno, gasolina), como se representa en la Figura\(\PageIndex{3}\).
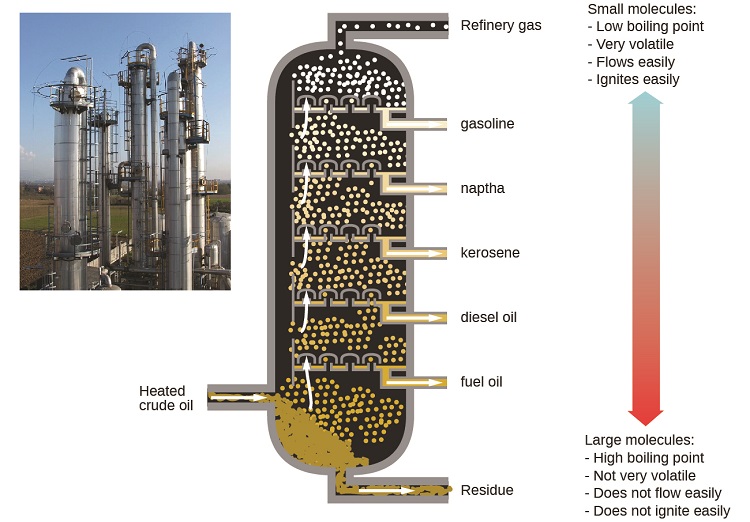
Depresión del Punto de Congelación de un Solvente
Las soluciones se congelan a temperaturas más bajas que los líquidos puros. Este fenómeno se explota en esquemas de “deshielo” que utilizan sal (Figura\(\PageIndex{4}\)), cloruro de calcio o urea para derretir hielo en carreteras y aceras, y en el uso del etilenglicol como “anticongelante” en radiadores de automóviles. El agua de mar se congela a una temperatura más baja que el agua dulce, por lo que los océanos Ártico y Antártico permanecen descongelados incluso a temperaturas inferiores a 0 °C (al igual que los fluidos corporales de peces y otros animales marinos de sangre fría que viven en estos océanos).

La disminución en el punto de congelación de una solución diluida en comparación con la del disolvente puro, Δ T f, se denomina depresión del punto de congelación y es directamente proporcional a la concentración molal del soluto
\[ΔT_\ce{f}=K_\ce{f}m \label{11.5.9} \]
donde
- \(m\)es la concentración molal del soluto en el disolvente y
- \(K_f\)se llama constante de depresión del punto de congelación (o constante crioscópica).
Al igual que para las constantes de elevación del punto de ebullición, estas son propiedades características cuyos valores dependen de la identidad química del disolvente. Los valores de K f para varios solventes se listan en la Tabla\(\PageIndex{1}\).
¿Cuál es el punto de congelación de la solución de 0.33 m de un soluto no electrolítico no volátil en benceno descrito en el Ejemplo\(\PageIndex{4}\)?
Solución
Utilice la ecuación que relaciona la depresión del punto de congelación con la molalidad del soluto para resolver este problema en dos pasos.

- Calcular el cambio en el punto de congelación. \[ΔT_\ce{f}=K_\ce{f}m=5.12\:°\ce C\:m^{−1}×0.33\:m=1.7\:°\ce C \nonumber \]
- Restar el cambio en el punto de congelación observado del punto de congelación del disolvente puro. \[\mathrm{Freezing\: Temperature=5.5\:°C−1.7\:°C=3.8\:°C} \nonumber \]
¿Cuál es el punto de congelación de una solución de 1.85 m de un soluto no electrolítico no volátil en nitrobenceno?
- Contestar
-
−9.3 °C
El cloruro de sodio y sus análogos del grupo 2, el cloruro de calcio y magnesio suelen utilizarse para descongelar calzadas y aceras, debido a que una solución de cualquiera de estas sales tendrá un punto de congelación inferior a 0 °C, el punto de congelación del agua pura. Las sales metálicas del grupo 2 se mezclan frecuentemente con el cloruro de sodio (“sal de roca”) más barato y fácilmente disponible para su uso en carreteras, ya que tienden a ser algo menos corrosivas que el NaCl, y proporcionan una mayor depresión del punto de congelación, ya que se disocian para producir tres partículas por unidad de fórmula, en lugar de dos partículas como el cloruro de sodio.
Debido a que estos compuestos iónicos tienden a acelerar la corrosión del metal, no serían una buena opción para usar en anticongelantes para el radiador de su automóvil o para descongelar un avión antes del despegue. Para estas aplicaciones, a menudo se utilizan compuestos covalentes, como el etileno o el propilenglicol. Los glicoles utilizados en el fluido del radiador no solo bajan el punto de congelación del líquido, sino que elevan el punto de ebullición, haciendo que el fluido sea útil tanto en invierno como en verano. Los glicoles calentados a menudo se rocían sobre la superficie de los aviones antes del despegue en las inclemencias del tiempo en el invierno para eliminar el hielo que ya se ha formado y evitar la formación de más hielo, lo que sería particularmente peligroso si se formara en las superficies de control de la aeronave (Video\(\PageIndex{1}\)).
Video\(\PageIndex{1}\): Se explota la depresión del punto de congelación para eliminar el hielo de las superficies de control de las aeronaves.
Diagrama de fases para una solución acuosa de un no electrolito
Los efectos colligativos sobre la presión de vapor, el punto de ebullición y el punto de congelación descritos en la sección anterior se resumen convenientemente comparando los diagramas de fase para un líquido puro y una solución derivada de ese líquido. Los diagramas de fases para el agua y una solución acuosa se muestran en la Figura\(\PageIndex{5}\).
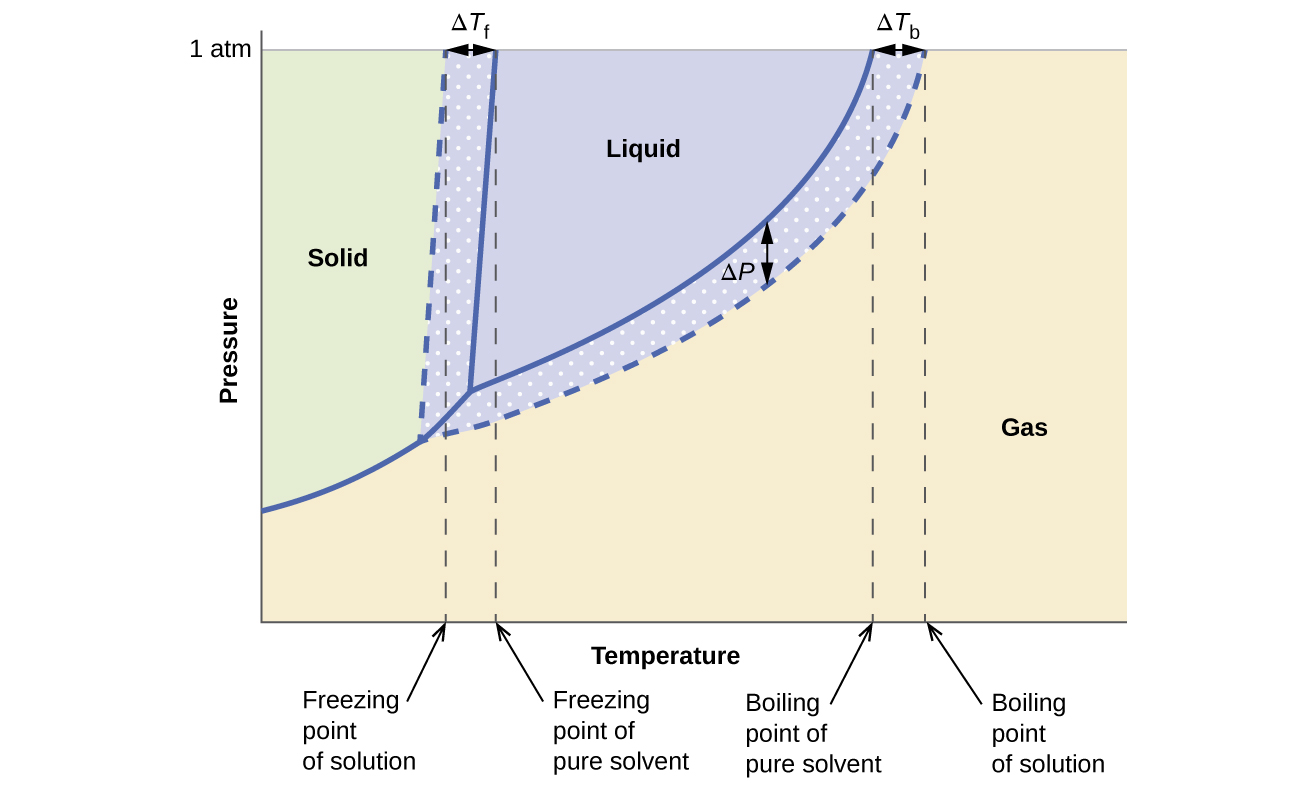
La curva líquido-vapor para la solución se ubica debajo de la curva correspondiente para el disolvente, representando la disminución de la presión de vapor, Δ P, que resulta de la disolución del soluto no volátil. En consecuencia, a cualquier presión dada, el punto de ebullición de la solución se observa a una temperatura mayor que la del disolvente puro, reflejando la elevación del punto de ebullición, Δ T b, asociada a la presencia de soluto no volátil. La curva sólido-líquido para la solución se desplaza a la izquierda de la del disolvente puro, representando la depresión del punto de congelación, Δ Tf, que acompaña a la formación de la solución. Finalmente, observe que las curvas sólido-gas para el disolvente y su solución son idénticas. Este es el caso de muchas soluciones que comprenden disolventes líquidos y solutos no volátiles. Al igual que para la vaporización, cuando una solución de este tipo se congela, en realidad son solo las moléculas de disolvente las que experimentan la transición de líquido a sólido, formando un disolvente sólido puro que excluye las especies de solutos. Las fases sólida y gaseosa, por lo tanto, están compuestas solo por disolvente, por lo que las transiciones entre estas fases no están sujetas a efectos coligativos.
Ósmosis y presión osmótica de soluciones
Varios materiales naturales y sintéticos exhiben permeación selectiva, lo que significa que solo moléculas o iones de cierto tamaño, forma, polaridad, carga, etc., son capaces de atravesar (permear) el material. Las membranas celulares biológicas proporcionan ejemplos elegantes de permeación selectiva en la naturaleza, mientras que los tubos de diálisis utilizados para eliminar los desechos metabólicos de la sangre son un ejemplo tecnológico más simplista. Independientemente de cómo se puedan fabricar, estos materiales generalmente se denominan membranas semipermeables.
Consideremos el aparato ilustrado en la Figura\(\PageIndex{6}\), en el que las muestras de disolvente puro y una solución están separadas por una membrana que solo las moléculas de disolvente pueden permear. Las moléculas de disolvente se difundirán a través de la membrana en ambas direcciones. Dado que la concentración de disolvente es mayor en el disolvente puro que en la solución, estas moléculas se difundirán desde el lado del disolvente de la membrana al lado de la solución a una velocidad más rápida que en la dirección inversa. El resultado es una transferencia neta de moléculas de disolvente del disolvente puro a la solución. La transferencia impulsada por difusión de moléculas de disolvente a través de una membrana semipermeable es un proceso conocido como ósmosis.
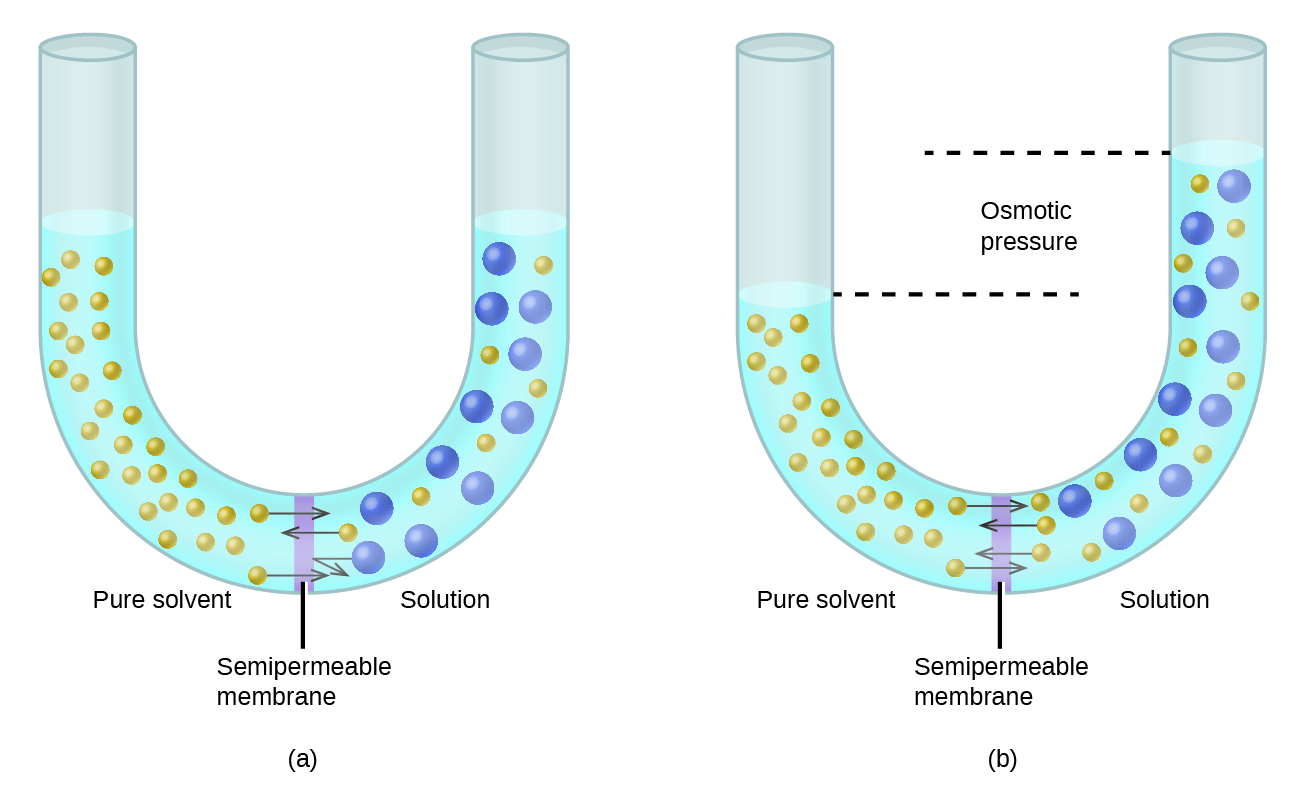
Cuando se realiza ósmosis en un aparato como el que se muestra en la Figura\(\PageIndex{6}\), el volumen de la solución aumenta a medida que se diluye por acumulación de disolvente. Esto hace que el nivel de la solución aumente, aumentando su presión hidrostática (debido al peso de la columna de solución en el tubo) y dando como resultado una transferencia más rápida de las moléculas de disolvente de nuevo al lado del disolvente puro. Cuando la presión alcanza un valor que produce una tasa de transferencia inversa de disolvente igual a la tasa de ósmosis, cesa la transferencia masiva de disolvente. Esta presión se denomina pressur osmótica e (\(\Pi\)) de la solución. La presión osmótica de una solución diluida se relaciona con su molaridad de soluto, M, y temperatura absoluta, T, según la ecuación
\[Π=MRT \label{11.5.10} \]
donde\(R\) esta la constante universal del gas.
¿Cuál es la presión osmótica (atm) de una solución 0.30 M de glucosa en agua que se utiliza para perfusión intravenosa a temperatura corporal, 37 °C?
Solución
Podemos encontrar la presión osmótica\(Π\), usando la Ecuación\ ref {11.5.10}, donde T está en la escala Kelvin (310 K) y el valor de R se expresa en unidades apropiadas (0.08206 L atm/mol K).
\ [\ begin {align*}
π&=MRT\\
&=\ mathrm {0.03\ :mol/l×0.08206\: L\: atm/mol\: K×310\: K}\\
&=\ mathrm {7.6\ :atm}
\ end {align*}\ nonumber\]
¿Cuál es la presión osmótica (atm) una solución con un volumen de 0.750 L que contiene 5.0 g de metanol, CH 3 OH, en agua a 37 °C?
- Contestar
-
5.3 atm
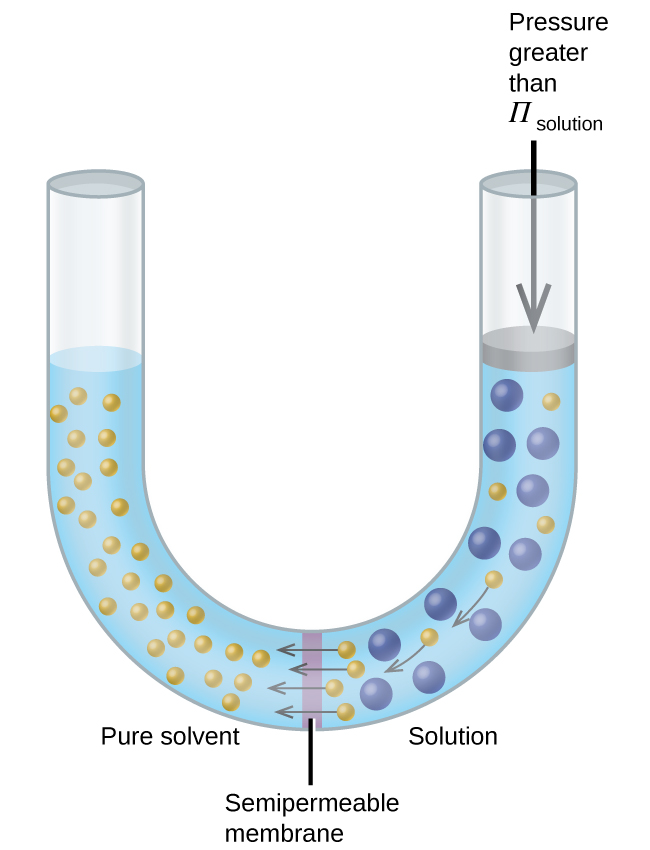
Si se coloca una solución en un aparato como el que se muestra en la Figura\(\PageIndex{7}\), aplicar una presión mayor que la presión osmótica de la solución invierte la ósmosis y empuja las moléculas de disolvente de la solución al disolvente puro. Esta técnica de ósmosis inversa se utiliza para la desalinización a gran escala de agua de mar y en escalas más pequeñas para producir agua del grifo de alta pureza para beber.
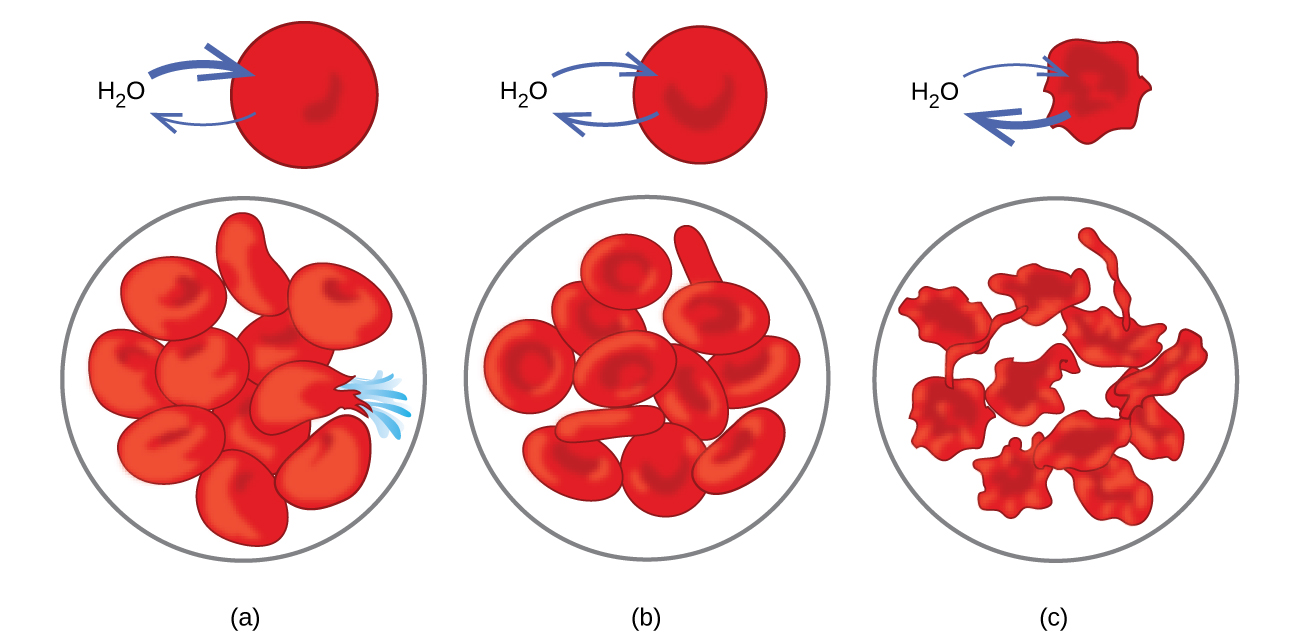
Ejemplos de ósmosis son evidentes en muchos sistemas biológicos debido a que las células están rodeadas por membranas semipermeables. Las zanahorias y el apio que se han vuelto flojos porque han perdido agua se pueden volver a hacer crujientes colocándolos en agua. El agua se mueve hacia las células de zanahoria o apio por ósmosis. Un pepino colocado en una solución salina concentrada pierde agua por ósmosis y absorbe algo de sal para convertirse en un pepinillo. La ósmosis también puede afectar a las células animales. Las concentraciones de soluto son particularmente importantes cuando las soluciones se inyectan en el cuerpo. Los solutos en los fluidos celulares corporales y el suero sanguíneo dan a estas soluciones una presión osmótica de aproximadamente 7.7 atm. Las soluciones inyectadas en el cuerpo deben tener la misma presión osmótica que el suero sanguíneo; es decir, deben ser isotónicas con el suero sanguíneo. Si se inyecta una solución menos concentrada, una solución hipotónica, en cantidad suficiente para diluir el suero sanguíneo, el agua del suero diluido pasa a las células sanguíneas por ósmosis, haciendo que las células se expandan y se rompan. Este proceso se llama hemólisis. Cuando se inyecta una solución más concentrada, una solución hipertónica, las células pierden agua a la solución más concentrada, se marchitan y posiblemente mueren en un proceso llamado crenación (Figura 11.5.8).
Determinación de Masas Molares
La presión osmótica y los cambios en el punto de congelación, punto de ebullición y presión de vapor son directamente proporcionales a la concentración de soluto presente. En consecuencia, podemos usar una medición de una de estas propiedades para determinar la masa molar del soluto a partir de las mediciones.
Se encuentra que una solución de 4.00 g de un no electrolito disuelto en 55.0 g de benceno se congela a 2.32 °C. ¿Cuál es la masa molar de este compuesto?
Solución
Podemos resolver este problema siguiendo los siguientes pasos.
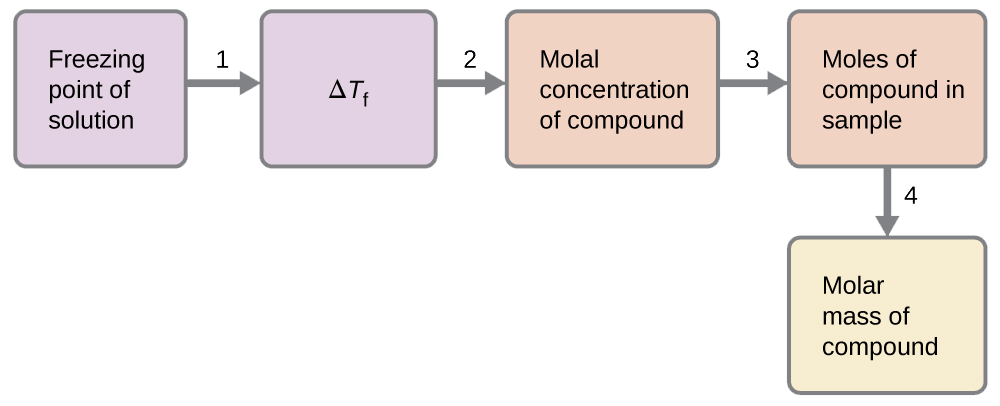
- Determinar el cambio en el punto de congelación desde el punto de congelación observado y el punto de congelación del benceno puro (Cuadro 11.5.1).
- Determinar la concentración molal a partir de K f, la constante de depresión del punto de congelación para benceno (Cuadro 11.5.1) y Δ T f.
\(ΔT_\ce{f}=K_\ce{f}m\)
\(m=\dfrac{ΔT_\ce{f}}{K_\ce{f}}=\dfrac{3.2\:°\ce C}{5.12\:°\ce C m^{−1}}=0.63\:m\)
- Determinar el número de moles de compuesto en la solución a partir de la concentración de molal y la masa de disolvente utilizada para elaborar la solución.
\(\mathrm{Moles\: of\: solute=\dfrac{0.62\:mol\: solute}{1.00\cancel{kg\: solvent}}×0.0550\cancel{kg\: solvent}=0.035\:mol}\)
- Determinar la masa molar a partir de la masa del soluto y el número de moles en esa masa.
\(\mathrm{Molar\: mass=\dfrac{4.00\:g}{0.034\:mol}=1.2×10^2\:g/mol}\)
Una solución de 35.7 g de un no electrolito en 220.0 g de cloroformo tiene un punto de ebullición de 64.5 °C. ¿Cuál es la masa molar de este compuesto?
- Contestar
-
1.8 × 10 2 g/mol
Una muestra de 0.500 L de una solución acuosa que contiene 10.0 g de hemoglobina tiene una presión osmótica de 5.9 torr a 22 °C. ¿Cuál es la masa molar de la hemoglobina?
Solución
Aquí hay un conjunto de pasos que se pueden utilizar para resolver el problema:

- \[\Pi=\mathrm{\dfrac{5.9\:torr×1\:atm}{760\:torr}=7.8×10^{−3}\:atm} \nonumber \]
\[\Pi=MRT \nonumber \]
\(M=\dfrac{Π}{RT}=\mathrm{\dfrac{7.8×10^{−3}\:atm}{(0.08206\:L\: atm/mol\: K)(295\:K)}=3.2×10^{−4}\:M}\)
- \(\mathrm{moles\: of\: hemoglobin=\dfrac{3.2×10^{−4}\:mol}{1\cancel{L\: solution}}×0.500\cancel{L\: solution}=1.6×10^{−4}\:mol}\)
- Determinar la masa molar a partir de la masa de hemoglobina y el número de moles en esa masa.
\(\mathrm{molar\: mass=\dfrac{10.0\:g}{1.6×10^{−4}\:mol}=6.2×10^4\:g/mol}\)
¿Cuál es la masa molar de una proteína si una solución de 0.02 g de la proteína en 25.0 mL de solución tiene una presión osmótica de 0.56 torr a 25 °C?
- Contestar
-
2.7 × 10 4 g/mol
Propiedades coligativas de los electrolitos
Como se señaló anteriormente en este módulo, las propiedades coligativas de una solución dependen únicamente del número, no del tipo, de especies de solutos disueltos. Por ejemplo, 1 mol de cualquier no electrolito disuelto en 1 kilogramo de disolvente produce la misma disminución del punto de congelación que 1 mol de cualquier otro no electrolito. Sin embargo, 1 mol de cloruro de sodio (un electrolito) forma 2 moles de iones cuando se disuelve en solución. Cada ión individual produce el mismo efecto sobre el punto de congelación que una sola molécula.
La concentración de iones en el agua de mar es aproximadamente la misma que la de una solución que contiene 4.2 g de NaCl disueltos en 125 g de agua. Supongamos que cada uno de los iones en la solución de NaCl tiene el mismo efecto sobre el punto de congelación del agua que una molécula no electrolítica, y determinar la temperatura de congelación de la solución (que es aproximadamente igual a la temperatura de congelación del agua de mar).
Solución
Podemos resolver este problema usando la siguiente serie de pasos.
- Convertir de gramos a moles de NaCl usando la masa molar de NaCl en el factor de conversión unitaria. Resultado: 0.072 mol NaCl
- Determinar el número de moles de iones presentes en la solución utilizando el número de moles de iones en 1 mol de NaCl como factor de conversión (2 mol iones/1 mol NaCl). Resultado: 0,14 moles de iones
- Determinar la molalidad de los iones en la solución a partir del número de moles de iones y la masa de disolvente, en kilogramos. Resultado: 1.1 m
- Utilice la proporcionalidad directa entre el cambio en el punto de congelación y la concentración de molal para determinar cuánto cambia el punto de congelación. Resultado: 2.0 °C
- Determinar el nuevo punto de congelación a partir del punto de congelación del solvente puro y el cambio. Resultado: −2.0 °C
Verificar cada resultado como una autoevaluación.
Supongamos que cada uno de los iones en el cloruro de calcio, CaCl 2, tiene el mismo efecto sobre el punto de congelación del agua que una molécula no electrolítica. Calcular el punto de congelación de una solución de 0.724 g de CaCl 2 en 175 g de agua.
- Contestar
-
−0.208 °C
Suponiendo una disociación completa, una solución acuosa de 1,0 m de NaCl contiene 2.0 moles de iones (1.0 mol Na + y 1.0 mol Cl −) por cada kilogramo de agua, y se espera que su depresión del punto de congelación sea
\[ΔT_\ce{f}=\mathrm{2.0\:mol\: ions/kg\: water×1.86\:°C\: kg\: water/mol\: ion=3.7\:°C.} \label{11.5.11} \]
Cuando se prepara realmente esta solución y se mide la depresión de su punto de congelación, sin embargo, se obtiene un valor de 3.4 °C. Se observan discrepancias similares para otros compuestos iónicos, y las diferencias entre los valores medidos y esperados de las propiedades coligativas típicamente se vuelven más significativas a medida que aumentan las concentraciones de soluto. Estas observaciones sugieren que los iones de cloruro de sodio (y otros electrolitos fuertes) no están completamente disociados en solución.
Para dar cuenta de esto y evitar los errores que acompañan al supuesto de disociación total, se utiliza un parámetro medido experimentalmente nombrado en honor al químico alemán ganador del Premio Nobel Jacobus Henricus van 't Hoff. El factor de van't Hoff (i) se define como la relación de partículas de soluto en solución al número de unidades de fórmula disueltas:
\[i=\dfrac{\textrm{moles of particles in solution}}{\textrm{moles of formula units dissolved}} \label{11.5.12} \]
Los valores para los factores de van't Hoff medidos para varios solutos, junto con los valores predichos que suponen disociación completa, se muestran en la Tabla\(\PageIndex{2}\).
| Electrolito | Partículas en Solución | i (Predicho) | i (Medido) |
|---|---|---|---|
| HCl | H +, Cl − | 2 | 1.9 |
| NaCl | Na +, Cl − | 2 | 1.9 |
| MgSO 4 | Mg 2 +,\(\ce{SO4^2-}\) | 2 | 1.3 |
| MgCl 2 | Mg 2 +, 2Cl − | 3 | 2.7 |
| FeCl 3 | Fe 3 +, 3Cl − | 4 | 3.4 |
| glucosa (un no electrolito) | C 12 H 22 O 11 | 1 | 1.0 |
En 1923, los químicos Peter Debye y Erich Hückel propusieron una teoría para explicar la aparente ionización incompleta de electrolitos fuertes. Sugirieron que aunque la atracción interiónica en una solución acuosa se reduce en gran medida por la solvatación de los iones y la acción aislante del disolvente polar, no se anula completamente. Las atracciones residuales impiden que los iones se comporten como partículas totalmente independientes (Figura\(\PageIndex{9}\)). En algunos casos, un ion positivo y negativo puede realmente tocarse, dando una unidad solvatada llamada par de iones. Así, la actividad, o la concentración efectiva, de cualquier tipo particular de ion es menor que la indicada por la concentración real. Los iones se separan cada vez más ampliamente cuanto más diluyen la solución, y las atracciones interiores residuales se vuelven cada vez menos. Así, en soluciones extremadamente diluidas, las concentraciones efectivas de los iones (sus actividades) son esencialmente iguales a las concentraciones reales. Tenga en cuenta que los factores van 't Hoff para los electrolitos en la Tabla\(\PageIndex{2}\) son para soluciones de 0.05 m, a cuya concentración el valor de i para NaCl es 1.9, a diferencia de un valor ideal de 2.
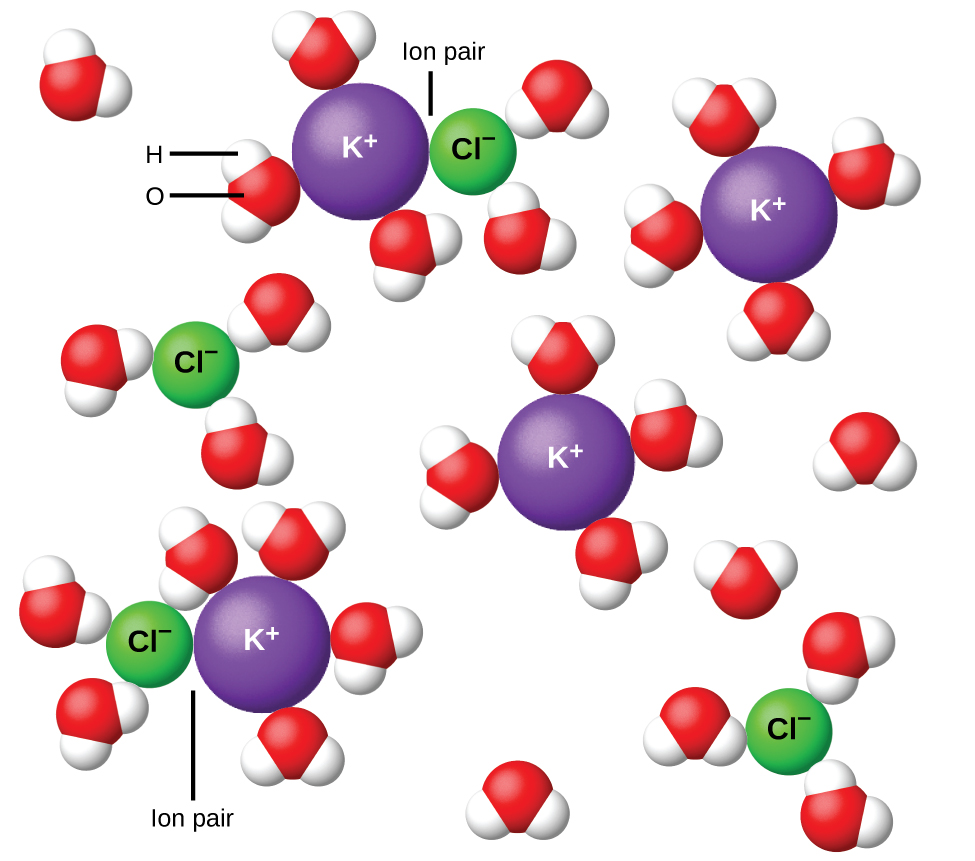
Resumen
Las propiedades de una solución que dependen únicamente de la concentración de partículas de soluto se denominan propiedades coligativas. Incluyen cambios en la presión de vapor, punto de ebullición y punto de congelación del disolvente en la solución. Las magnitudes de estas propiedades dependen únicamente de la concentración total de partículas de soluto en solución, no del tipo de partículas. La concentración total de partículas de soluto en una solución también determina su presión osmótica. Esta es la presión que se debe aplicar a la solución para evitar la difusión de moléculas de disolvente puro a través de una membrana semipermeable hacia la solución. Los compuestos iónicos pueden no disociarse completamente en solución debido a los efectos de la actividad, en cuyo caso los efectos coligativos observados pueden ser menores de lo predicho.
Ecuaciones Clave
- \(\left(P_\ce{A}=X_\ce{A}P^\circ_\ce{A}\right)\)
- \(P_\ce{solution}=\sum_{i}P_i=\sum_{i}X_iP^\circ_i\)
- \(P_\ce{solution}=X_\ce{solvent}P^\circ_\ce{solvent}\)
- Δ T b = K b m
- Δ T f = K f m
- Π = MRT
Notas al pie
- Se muestra un no electrolito para comparación.
Glosario
- elevación del punto de ebullición
- elevación del punto de ebullición de un líquido por adición de un soluto
- constante de elevación del punto de ebullición
- la constante de proporcionalidad en la ecuación que relaciona la elevación del punto de ebullición con la molalidad del soluto; también conocida como la constante ebuloscópica
- propiedad coligativa
- propiedad de una solución que depende únicamente de la concentración de una especie de soluto
- crenation
- proceso mediante el cual las células biológicas se marchitan debido a la pérdida de agua por ósmosis
- depresión del punto de congelación
- disminución del punto de congelación de un líquido mediante la adición de un soluto
- constante de depresión del punto de congelación
- (también, constante crioscópica) constante de proporcionalidad en la ecuación que relaciona la depresión del punto de congelación con la molalidad del soluto
- hemólisis
- ruptura de glóbulos rojos por acumulación de exceso de agua por ósmosis
- hipertónico
- de mayor presión osmótica
- hipotónico
- de menor presión osmótica
- par de iones
- par anión/catión solvatados unidos por atracción electrostática moderada
- isotónico
- de igual presión osmótica
- molalidad (m)
- una unidad de concentración definida como la relación de los números de moles de soluto a la masa del disolvente en kilogramos
- ósmosis
- difusión de moléculas de disolvente a través de una membrana semipermeable
- presión osmótica (π)
- presión opuesta requerida para evitar la transferencia masiva de moléculas de disolvente a través de una membrana semipermeable
- Ley de Raoult
- la presión parcial ejercida por un componente de solución es igual al producto de la fracción molar del componente en la solución y su presión de vapor de equilibrio en estado puro
- membrana semipermeable
- una membrana que permite selectivamente el paso de ciertos iones o moléculas
- factor van 't Hoff (i)
- la relación entre el número de moles de partículas en una solución y el número de moles de unidades de fórmula disueltas en la solución


