21.1: Estructura y estabilidad nuclear

Objetivos de aprendizaje

• Describir la estructura nuclear en términos de protones, neutrones y electrones
• Calcular el defecto de masa y la energía de unión para núcleos
• Explicar las tendencias en la estabilidad relativa de los núcleos

La química nuclear es el estudio de reacciones que implican cambios en la estructura nuclear. El capítulo sobre átomos, moléculas e iones introdujo la idea básica de la estructura nuclear, que el núcleo de un átomo está compuesto por protones y, con la excepción de\(\ce{^1_1H}\), neutrones. Recordemos que el número de protones en el núcleo se llama el número atómico (\(Z\)) del elemento, y la suma del número de protones y el número de neutrones es el número de masa (\(A\)). Los átomos con el mismo número atómico pero diferentes números de masa son isótopos del mismo elemento. Cuando nos referimos a un solo tipo de núcleo, a menudo usamos el término nucleido y lo identificamos por la notación:

\[\ce{^{A}_{Z}X} \label{Eq1} \]

donde

• \(X\)es el símbolo del elemento,
• \(A\)es el número de masa, y
• \(Z\)es el número atómico.

A menudo, un nucleido es referenciado por el nombre del elemento seguido de un guión y el número de masa. Por ejemplo,\(\ce{^{14}_6C}\) se llama “carbono-14".

Los protones y neutrones, llamados colectivamente nucleones, están agrupados firmemente en un núcleo. Con un radio de aproximadamente 10 ⁻¹⁵ metros, un núcleo es bastante pequeño en comparación con el radio de todo el átomo, que es de aproximadamente 10 ⁻¹⁰ metros. Los núcleos son extremadamente densos en comparación con la materia a granel, promediando\(1.8 \times 10^{14}\) gramos por centímetro cúbico. Por ejemplo, el agua tiene una densidad de 1 gramo por centímetro cúbico, y el iridio, uno de los elementos más densos conocidos, tiene una densidad de 22.6 g/cm ³. Si la densidad de la tierra fuera igual a la densidad nuclear promedio, el radio de la tierra sería de solo unos 200 metros (el radio real de la tierra es aproximadamente\(6.4 \times 10^6\) metros, 30,000 veces mayor). \(\PageIndex{1}\)El ejemplo demuestra cuán grandes densidades nucleares pueden ser en el mundo natural.

Ejemplo\(\PageIndex{1}\): Neutron Stars

Densidad de una estrella de neutrones Las estrellas de neutrones se forman cuando el núcleo de una estrella muy masiva sufre un colapso gravitacional, lo que hace que las capas externas de la estrella exploten en una supernova. Compuestas casi en su totalidad por neutrones, son las estrellas más densas conocidas en el universo, con densidades comparables a la densidad promedio de un núcleo atómico. Una estrella de neutrones en una galaxia lejana tiene una masa igual a 2.4 masas solares (1 masa solar\(M_☉\) = = masa del sol =\(\mathrm{1.99 \times 10^{30}\; kg}\)) y un diámetro de 26 km.

1. ¿Cuál es la densidad\(\rho\) de esta estrella de neutrones?
2. ¿Cómo se compara la densidad de esta estrella de neutrones con la densidad de un núcleo de uranio, que tiene un diámetro de aproximadamente 15 fm (1 fm = 10 ^—15 m)?

Solución

Podemos tratar tanto a la estrella de neutrones como al núcleo U-235 como esferas. Entonces la densidad para ambos viene dada por:

\[\rho = \dfrac{m}{V} \nonumber \]

con

\[V = \dfrac{4}{3} \pi r^3 \nonumber \]

(a) El radio de la estrella de neutrones es\(\mathrm{\dfrac{1}{2}\times 26\; km = \dfrac{1}{2} \times 2.6 \times 10^4\; m = 1.3 \times 10^4\; m}\) por lo que la densidad de la estrella de neutrones es:

\[ \begin{align*} \rho &= \dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{2.4(1.99 \times 10^{30}\;kg)}{\frac{4}{3} \pi (1.3 \times 10^4m)^3} \\[4pt] &=5.2 \times 10^{17}\;kg/m^3 \end{align*} \nonumber \]

b) El radio del núcleo U-235 es\(\mathrm{\dfrac{1}{2} \times 15 \times 10^{−15}\;m=7.5 \times 10^{−15}\;m}\), por lo que la densidad del núcleo U-235 es:

\[ \begin{align*} \rho &=\dfrac{m}{V} \\[4pt] &=\dfrac{m}{\frac{4}{3}\pi r^3} \\[4pt] &= \dfrac{235\;amu \left(\frac{1.66 \times 10^{-27}\;kg}{1\;amu}\right)}{ \frac{4}{3} \pi (7.5 \times 10^{-15}m)^3} \\[4pt] &=2.2 \times 10^{17} \; kg/m^3 \end{align*} \nonumber \]

Estos valores son bastante similares (mismo orden de magnitud), pero el núcleo es más del doble de denso que la estrella de neutrones.

Ejercicio\(\PageIndex{1}\)

Encuentra la densidad de una estrella de neutrones con una masa de 1.97 masas solares y un diámetro de 13 km, y compárela con la densidad de un núcleo de hidrógeno, que tiene un diámetro de 1.75 fm (\(\mathrm{1\; fm = 1 \times 10^{–15}\; m}\)).

Contestar

La densidad de la estrella de neutrones es\(\mathrm{3.4 \times 10^{18}\; kg/m^3}\). La densidad de un núcleo de hidrógeno es\(\mathrm{6.0 \times 10^{17}\; kg/m^3}\). La estrella de neutrones es 5.7 veces más densa que el núcleo de hidrógeno.

Para mantener juntos los protones cargados positivamente en el volumen muy pequeño de un núcleo se requieren fuerzas atractivas muy fuertes porque los protones cargados positivamente se repelen fuertemente entre sí a distancias tan cortas. La fuerza de atracción que mantiene unido al núcleo es la fuerza nuclear fuerte. (La fuerza fuerte es una de las cuatro fuerzas fundamentales que se sabe que existen. Las otras son la fuerza electromagnética, la fuerza gravitacional y la fuerza nuclear débil). Esta fuerza actúa entre protones, entre neutrones, y entre protones y neutrones. Es muy diferente de la fuerza electrostática que retiene electrones cargados negativamente alrededor de un núcleo cargado positivamente (la atracción entre cargas opuestas). En distancias inferiores a 10 ⁻¹⁵ metros y dentro del núcleo, la fuerza nuclear fuerte es mucho más fuerte que las repulsiones electrostáticas entre protones; a distancias mayores y fuera del núcleo, es esencialmente inexistente.

Energía Nuclear Vinculante

Como ejemplo sencillo de la energía asociada a la fuerte fuerza nuclear, consideremos el átomo de helio compuesto por dos protones, dos neutrones y dos electrones. La masa total de estas seis partículas subatómicas puede calcularse como:

\[ \underset{\Large\text{protons}}{(2 \times 1.0073\; \text{amu})} + \underset{\Large\text{neutrons}}{(2 \times 1.0087\; \text{amu})} + \underset{\Large\text{electrons}}{(2 \times 0.00055\; \text{amu})}= 4.0331\; \text{amu }\label{Eq2} \]

Sin embargo, las mediciones espectrométricas de masas revelan que la masa de un\(\ce{_2^4 He}\) átomo es de 4.0026 amu, menor que las masas combinadas de sus seis partículas subatómicas constituyentes. Esta diferencia entre las masas calculadas y medidas experimentalmente se conoce como el defecto de masa del átomo. En el caso del helio, el defecto de masa indica una “pérdida” en masa de 4.0331 amu — 4.0026 amu = 0.0305 amu. La pérdida de masa que acompaña a la formación de un átomo a partir de protones, neutrones y electrones se debe a la conversión de esa masa en energía que se desarrolla a medida que se forma el átomo. La energía de unión nuclear es la energía producida cuando los nucleones de los átomos están unidos entre sí; esta es también la energía necesaria para romper un núcleo en sus protones y neutrones constituyentes. En comparación con las energías de enlace químico, las energías de unión nuclear son enormemente mayores, como aprenderemos en esta sección. En consecuencia, los cambios energéticos asociados con las reacciones nucleares son enormemente mayores que los de las reacciones químicas.

La conversión entre masa y energía se representa de manera más identificable por la ecuación de equivalencia masa-energía como lo afirma Albert Einstein:

\[E=mc^2 \label{Eq3} \]

donde E es energía, m es la masa de la materia que se está convirtiendo, y c es la velocidad de la luz en un vacío. Esta ecuación puede ser utilizada para encontrar la cantidad de energía que resulta cuando la materia se convierte en energía. Usando esta ecuación de equivalencia masa-energía, la energía de unión nuclear de un núcleo puede calcularse a partir de su defecto másico, como se demuestra en el Ejemplo\(\PageIndex{2}\). Una variedad de unidades se utilizan comúnmente para las energías de unión nuclear, incluyendo electrón voltios (eV), con 1 eV igualando la cantidad de energía necesaria para el movimiento de la carga de un electrón a través de una diferencia de potencial eléctrico de 1 voltio, haciendo\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\).

Ejemplo\(\PageIndex{2}\): Calculation of Nuclear Binding Energy

Determinar la energía de unión para el nucleido\(\ce{^4_2 He}\) en:

1. julios por mol de núcleos
2. julios por núcleo
3. MeV por núcleo

Solución

El defecto de masa para un\(\ce{^4_2He}\) núcleo es de 0.0305 amu, como se mostró anteriormente. Determinar la energía de unión en julios por nucleido usando la ecuación de equivalencia masa-energía. Para acomodar las unidades de energía solicitadas, el defecto de masa debe expresarse en kilogramos (recuerde que 1 J = 1 kg m ^{2 /s 2} /s ²).

(a) Primero, expresar el defecto de masa en g/mol. Esto se hace fácilmente considerando la equivalencia numérica de la masa atómica (amu) y la masa molar (g/mol) que resulta de las definiciones de las unidades de amu y mol (consulte la discusión previa en el capítulo sobre átomos, moléculas e iones si es necesario). Por lo tanto, el defecto de masa es de 0.0305 g/mol. Para acomodar las unidades de los otros términos en la ecuación masa-energía, la masa debe expresarse en kg, ya que 1 J = 1 kg m ² /s ². Convertir gramos en kilogramos produce un defecto de masa de\(\mathrm{3.05 \times 10^{–5}\; kg/mol}\). Sustituir esta cantidad en la ecuación de equivalencia masa-energía produce:

\[\begin{align*} E &=mc^2 \\[4pt] &= \dfrac{3.05 \times 10^{-5}\;kg}{mol} \times \left(\dfrac{2.998 \times 10^8\;m}{s}\right)^2 \\[4pt] &= 2.74×10^{12}\:kg\:m^2s^{-2}mol^{-1} \\[4pt] &=2.74 \times 10^{12}\;J/mol=2.74\: TJ /mol \end{align*} \nonumber \]

Tenga en cuenta que esta tremenda cantidad de energía se asocia con la conversión de una cantidad muy pequeña de materia (alrededor de 30 mg, aproximadamente la masa de gota típica de agua).

(b) La energía de unión para un solo núcleo se calcula a partir de la energía de unión molar usando el número de Avogadro:

\[\begin{align*} E &= 2.74×10^{12}\:J\:mol^{-1}×\dfrac{1\: mol}{6.022×10^{23}\:nuclei} \\[4pt] &=4.55×10^{-12} \: J =4.55\: pJ \end{align*} \nonumber \]

c) Recordemos eso\(\mathrm{1\; eV = 1.602 \times 10^{-19}\; J}\). Usando la energía de enlace calculada en la parte (b):

\[\begin{align*} E &= 4.55×10^{-12} \: J× \dfrac{1\: eV}{1.602×10^{-19}\:J} \\[4pt] &=2.84×10^7\:eV=28.4\: MeV \end{align*} \nonumber \]

Ejercicio\(\PageIndex{2}\)

¿Cuál es la energía de unión para el nucleido\(\ce{^{19}_9F}\) (masa atómica: 18.9984 amu) en MeV por núcleo?

Contestar

148.4 MeV

Debido a que los cambios de energía para romper y formar enlaces son tan pequeños en comparación con los cambios de energía para romper o formar núcleos, los cambios en la masa durante todas las reacciones químicas ordinarias son prácticamente indetectables. Como se describe en el capítulo sobre termoquímica, las reacciones químicas más energéticas exhiben entalpías del orden de miles de kJ/mol, lo que equivale a diferencias de masa en el rango de nanogramos (10 ^—9 g). Por otro lado, las energías de unión nuclear suelen ser del orden de miles de millones de kJ/mol, correspondientes a diferencias de masa en el rango de miligramos (10 ^—3 g).

Estabilidad Nuclear

Un núcleo es estable si no puede transformarse en otra configuración sin agregar energía desde el exterior. De los miles de nucleidos que existen, alrededor de 250 son estables. Una gráfica del número de neutrones versus el número de protones para núcleos estables revela que los isótopos estables caen en una banda estrecha. Esta región es conocida como la banda de estabilidad (también llamada cinturón, zona o valle de estabilidad). La línea recta en la Figura\(\PageIndex{1}\) representa núcleos que tienen una relación 1:1 de protones a neutrones (relación n:p). Obsérvese que los núcleos estables más ligeros, en general, tienen igual número de protones y neutrones. Por ejemplo, el nitrógeno-14 tiene siete protones y siete neutrones. Sin embargo, los núcleos estables más pesados tienen cada vez más neutrones que protones. Por ejemplo: el hierro-56 tiene 30 neutrones y 26 protones, una relación n:p de 1.15, mientras que el nucleido estable plomo-207 tiene 125 neutrones y 82 protones, una relación n:p igual a 1.52. Esto se debe a que los núcleos más grandes tienen más repulsiones protón-protón, y requieren un mayor número de neutrones para proporcionar fuerzas fuertes compensadoras para superar estas repulsiones electrostáticas y mantener el núcleo unido.

Figura\(\PageIndex{1}\): Esta gráfica muestra los nucleidos que se sabe que existen y los que son estables. Los nucleidos estables se indican en azul, y los nucleidos inestables se indican en verde. Obsérvese que todos los isótopos de elementos con números atómicos mayores a 83 son inestables. La línea continua es la línea donde n = Z.

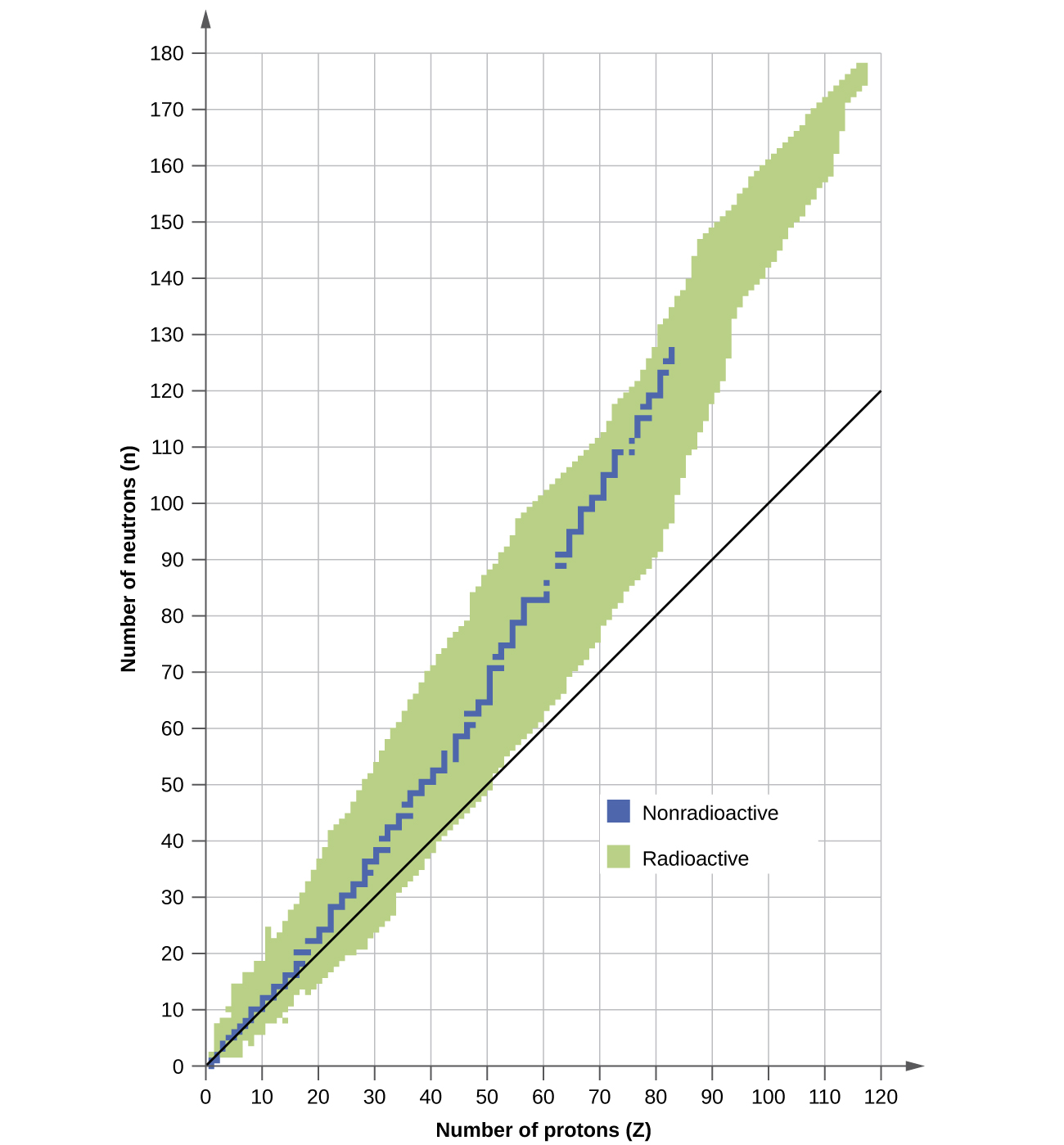
Los núcleos que están a la izquierda o a la derecha de la banda de estabilidad son inestables y exhiben radiactividad. Cambian espontáneamente (desintegración) en otros núcleos que están en, o más cerca de, la banda de estabilidad. Estas reacciones de desintegración nuclear convierten un isótopo inestable (o radioisótopo) en otro, más estable, isótopo. Discutiremos la naturaleza y los productos de esta desintegración radiactiva en secciones posteriores de este capítulo.

Se pueden hacer varias observaciones respecto a la relación entre la estabilidad de un núcleo y su estructura. Los núcleos con números pares de protones, neutrones o ambos tienen más probabilidades de ser estables (Tabla\(\PageIndex{1}\)). Los núcleos con cierto número de nucleones, conocidos como números mágicos, son estables contra la desintegración nuclear. Estos números de protones o neutrones (2, 8, 20, 28, 50, 82 y 126) hacen conchas completas en el núcleo. Estos son similares en concepto a las conchas de electrones estables observadas para los gases nobles. Núcleos que tienen números mágicos tanto de protones como de neutrones\(\ce{^4_2He}\)\(\ce{^{16}_8O}\), como\(\ce{^{40}_{20}Ca}\),,\(\ce{^{208}_{82}Pb}\) y son particularmente estables. Estas tendencias en la estabilidad nuclear pueden racionalizarse considerando un modelo mecánico cuántico de estados de energía nuclear análogo al utilizado para describir estados electrónicos anteriormente en este libro de texto. Los detalles de este modelo están fuera del alcance de este capítulo.

Tabla\(\PageIndex{1}\): Isótopos nucleares estables

Número de isótopos estables	Número de protones	Número de neutrones
157	incluso	incluso
53	incluso	impar
50	impar	incluso
5	impar	impar

La estabilidad relativa de un núcleo se correlaciona con su energía de unión por nucleón, la energía de unión total para el núcleo dividida por el número o nucleones en el núcleo. Por ejemplo, la energía de unión para un\(\ce{^4_2He}\) núcleo es, por lo tanto:

\[\mathrm{\dfrac{28.4\; MeV}{4\; nucleons}=7.10\; MeV/nucleon} \label{Eq3a} \]

La energía de unión por nucleón de un nucleido en la curva mostrada en la Figura\(\PageIndex{2}\)

Figura\(\PageIndex{2}\): La energía de unión por nucleón es mayor para los nucleidos con un número de masa de aproximadamente 56.

Ejemplo\(\PageIndex{3}\): Calculation of Binding Energy per Nucleon

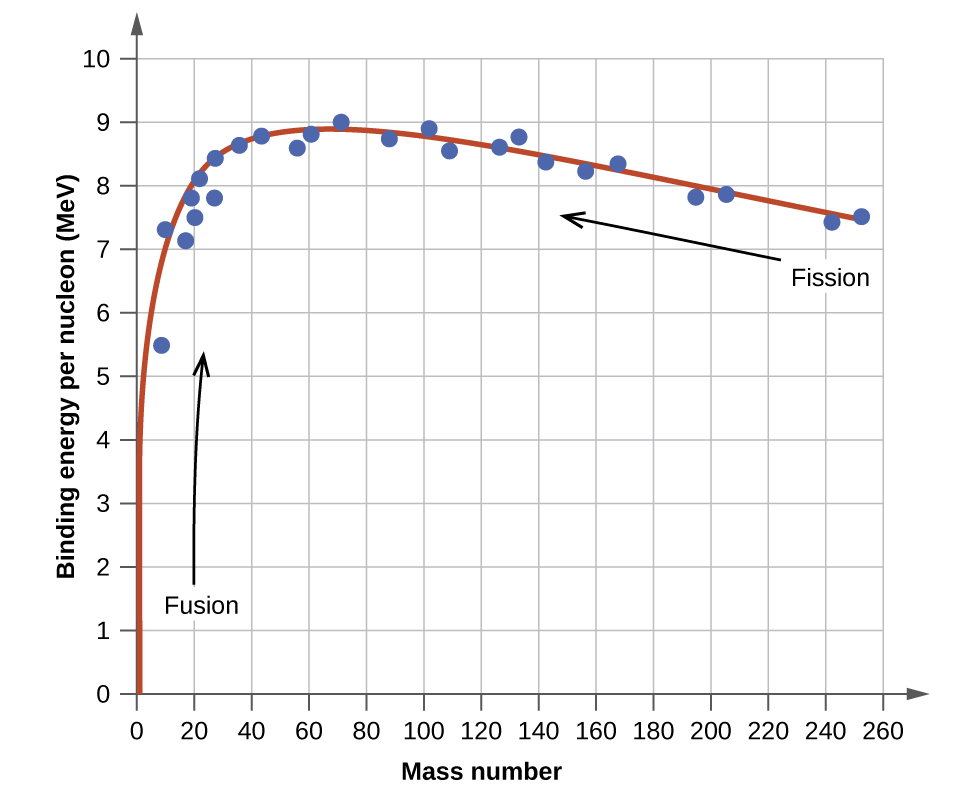
El nucleido de hierro\(\ce{^{56}_{26}Fe}\) se encuentra cerca de la parte superior de la curva de energía de unión (Figura\(\PageIndex{2}\)) y es uno de los nucleidos más estables. ¿Cuál es la energía de unión por nucleón (en MeV) para el nucleido\(\ce{^{56}_{26}Fe}\) (masa atómica de 55.9349 amu)?

Solución

Al igual que en Ejemplo, primero determinamos el defecto de masa del nucleido, que es la diferencia entre la masa de 26 protones, 30 neutrones y 26 electrones, y la masa observada de un\(\ce{^{56}_{26}Fe}\) átomo:

\ [\ begin {align*}
\ mathrm {Mass\: defecto} &=\ mathrm {[(26×1.0073\: amu) + (30×1.0087\: amu) + (26×0.00055\: amu)] −55.9349\: amu}\\
&=\ mathrm {56.4651\: amu−55.9349\: amu}\\
&=\ mathrm {0.5302\: amu}
\ end {align*}\ nonumber\]

A continuación calculamos la energía de unión para un núcleo a partir del defecto de masa usando la ecuación de equivalencia masa-energía:

\ [\ begin {align*}
E&=mc^2=\ mathrm {0.5302\: amu×\ dfrac {1.6605×10^ {-27}\ :kg} {1\: amu} × (2.998×10^8\ :m/s) ^2}\\
&=\ mathrm {7.913×10^ {−11}\:\ textrm {kgm} /s^2}\\
&=\ mathrm {7.913×10^ {−11}\ :J}
\ end {align*}\ nonumber\]

Luego convertimos la energía de unión en julios por núcleo en unidades de MeV por nucleido:

\[\mathrm{7.913×10^{−11}\:J×\dfrac{1\: MeV}{1.602×10^{−13}\:J}=493.9\: MeV} \nonumber \]

Finalmente, determinamos la energía de unión por nucleón dividiendo la energía nuclear total de unión por el número de nucleones en el átomo:

\[\textrm{Binding energy per nucleon}=\mathrm{\dfrac{493.9\: MeV}{56}=8.820\: MeV/nucleon} \nonumber \]

Tenga en cuenta que esto es casi 25% más grande que la energía de unión por nucleón para\(\ce{^4_2He}\). (Obsérvese también que este es el mismo proceso que en el Ejemplo\ (\ PageIndex {2}\, pero con el paso adicional de dividir la energía nuclear total de unión por el número de nucleones.)

Ejercicio\(\PageIndex{3}\)

¿Cuál es la energía de unión por nucleón en\(\ce{^{19}_9F}\) (masa atómica, 18.9984 amu)?

Contestar

7.810 MEV/Nucleón

Resumen

Un núcleo atómico consiste en protones y neutrones, llamados colectivamente nucleones. Aunque los protones se repelen entre sí, el núcleo se mantiene firmemente unido por una fuerza de corto alcance, pero muy fuerte, llamada fuerza nuclear fuerte. Un núcleo tiene menos masa que la masa total de sus nucleones constituyentes. Esta masa “faltante” es el defecto de masa, que se ha convertido en la energía de unión que mantiene unido al núcleo de acuerdo con la ecuación de equivalencia masa-energía de Einstein, E = mc ². De los muchos nucleidos que existen, sólo un pequeño número son estables. Los nucleidos con números pares de protones o neutrones, o aquellos con números mágicos de nucleones, son especialmente propensos a ser estables. Estos nucleidos estables ocupan una estrecha banda de estabilidad en una gráfica de número de protones versus número de neutrones. La energía de unión por nucleón es mayor para los elementos con números de masa cercanos a 56; estos son los núcleos más estables.

Ecuaciones Clave

• E = mc ²

Glosario

banda de estabilidad

(también, cinturón de estabilidad, zona de estabilidad o valle de estabilidad) región del gráfico del número de protones versus número de neutrones que contienen nucleidos estables (no radiactivos)

energía de unión por nucleón

energía total de unión para el núcleo dividida por el número de nucleones en el núcleo

electrón voltio (eV)

unidad de medición de energías de unión nuclear, con 1 eV equivalente a la cantidad de energía debido al movimiento de un electrón a través de una diferencia de potencial eléctrico de 1 voltio

número mágico

núcleos con números específicos de nucleones que están dentro de la banda de estabilidad

defecto de masa

diferencia entre la masa de un átomo y la masa sumada de sus partículas subatómicas constituyentes (o la masa “perdida” cuando los nucleones se juntan para formar un núcleo)

ecuación de equivalencia masa-energía

La relación de Albert Einstein demuestra que la masa y la energía son equivalentes

energía nuclear vinculante

energía perdida cuando los nucleones de un átomo están unidos entre sí (o la energía necesaria para romper un núcleo en sus protones y neutrones constituyentes)

química nuclear

estudio de la estructura de núcleos atómicos y procesos que cambian la estructura nuclear

nucleón

término colectivo para protones y neutrones en un núcleo

nucleido

núcleo de un isótopo particular

radiactividad

fenómeno exhibido por un nucleón inestable que experimenta espontáneamente un cambio en un nucleón que es más estable; se dice que un nucleón inestable es radiactivo

radioisótopo

isótopo que es inestable y se convierte en un isótopo diferente y más estable

fuerza nuclear fuerte

fuerza de atracción entre nucleones que mantiene unido un núcleo

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).