6.13: Celosías Bravais y Empaque de Cristal

Última actualización
Guardar como PDF

Page ID: 79875

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Celosías Bravais

Para describir un cristal se necesitan dos ingredientes: una celosía y una base. Dicho de otra manera, la celosía describe cómo se disponen espacialmente los átomos: en un cristal, es un patrón regular y ordenado que tesela el espacio 3D. La base es la unidad que se copia sobre el patrón: generalmente consiste en uno o más átomos. Los cristalógrafos utilizan un conjunto de patrones llamados celosías de Bravais para describir las formas en que los átomos pueden disponerse para formar sólidos cristalinos. En\(3.091\), nos centraremos en el subconjunto de las celosías Bravais que son cúbicas: la escala en las tres dimensiones es la misma.

Hay tres celosías cúbicas: cúbicas simples (SC), cúbicas centradas en el cuerpo (BCC) y cúbicas centradas en la cara (FCC).

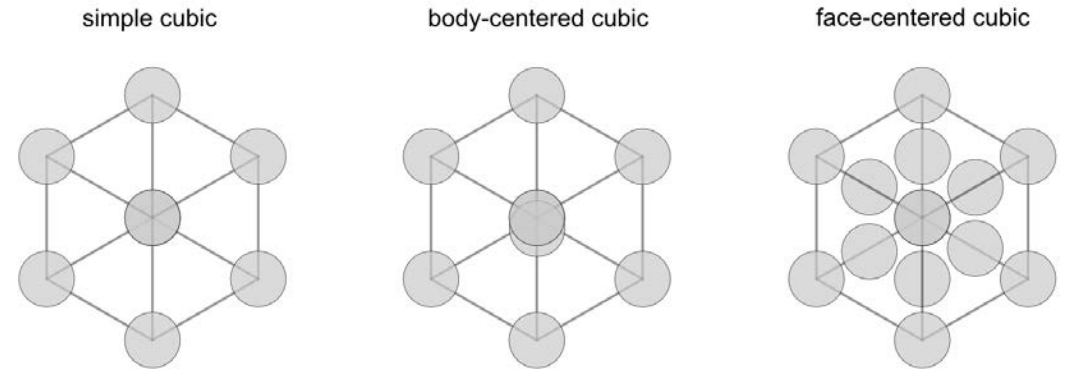
Screen Shot 2022-09-07 en 1.28.18 AM.png

En la figura anterior, la cuadrícula gris muestra el contorno de la celda unitaria, mientras que cada círculo representa un átomo. Para los átomos a lo largo de las esquinas de la celda unitaria, cada átomo se comparte entre ocho celdas vecinas, por lo que cada celda contiene\(1 / 8\) de un átomo. De manera similar, cada uno de los átomos faciales en la celda unitaria FCC se comparten entre dos celdas, por lo que cada\(1 / 2\) una contiene un átomo. Podemos calcular cuántos átomos hay en cada una de las celdas unitarias cúbicas:

\(N_{S C}=8\)\(* \dfrac{1}{8}\)átomos de esquina por\(=1\) átomo de esquina por celda\(\mathrm{SC}\) unitaria

\(N_{B C C}=8\)\(* \dfrac{1}{8}\)átomos de esquina por átomo\(+1\) central de esquina\(=2\) átomos por celda unitaria BCC

\(N_{F C C}=8\)esquinas\(* \dfrac{1}{8}\) átomos por esquina átomos de\(+6\) cara\(* \dfrac{1}{2}\) átomos por\(=4\) átomo facial por celda\(\mathrm{FCC}\) unitaria

Empaque de cristal

Ahora podemos definir algunas métricas relevantes para describir la densidad atómica en diferentes celosías e incluso a lo largo de diferentes direcciones dentro del cristal. Hablaremos de densidad tanto en términos de área como de volumen. Para definir algunos términos:

densidad de empaque: relación entre el espacio ocupado por átomos y el espacio total disponible. Las unidades son\(\left[\frac{\text { atoms }}{n m^2}\right]\) (por área) o\(\left[\frac{\text { atoms }}{n m^3}\right]\) por volumen
factor de empaquetamiento atómico: fracción del espacio ocupado por átomos, en 2D (relación de área) o 3D (relación de volumen). Es un valor sin unidades entre 0 y 1.

También necesitamos recordar algunas cosas de la geometría: el área de un círculo es\(\pi r^2\), y el volumen de una esfera lo es\(\frac{4}{3} \pi r^3\). Para un sistema cúbico con longitud lateral\(a\) tiene longitud diagonal de cara\(\sqrt{2} * a\) y longitud diagonal del cuerpo\(\sqrt{3} * a\). El truco para resolver con éxito las preguntas de empaque es poder relacionar el radio de los átomos (asumiendo que son esferas duras y lo más empaquetadas posible) y la longitud lateral de la celda unitaria. A partir de ahí, es solo un poco de álgebra para encontrar la solución.

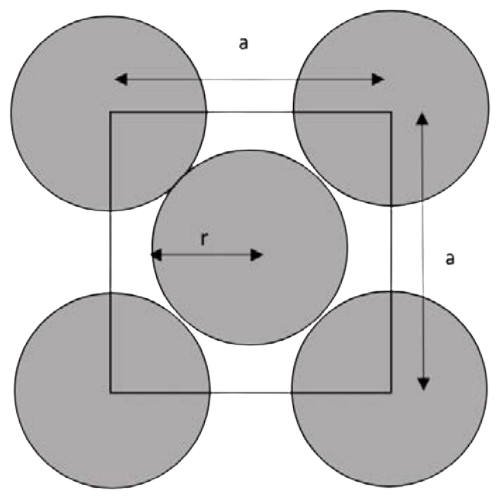
Ejemplo: A continuación se muestra una sección de una celda unitaria FCC: es un corte de una cara. Primero, encontrar la relación entre el radio de los átomos,\(r\), y el ancho de celda unitaria,\(a\). Después, determine cuántos átomos hay en la celda\(2 \mathrm{D}\) unitaria. Finalmente, calcular la densidad de empaquetamiento de este plano (suponiendo\(a=3.5 \AA\)), y la fracción de empaquetamiento atómico 2D.

Screen Shot 2022-09-07 en 1.34.30 AM.png

Contestar

Primero, tenemos que\(r\) relacionarnos con\(a\). La forma más fácil de hacerlo suele ser mirar a lo largo de la dirección empaquetada más cercana: aquí, si bajamos una diagonal, los átomos siempre están en contacto a lo largo de su centro.

\[r+2 r+r=\sqrt{2} * a \nonumber\]

\[r=\dfrac{\sqrt{2}}{4} a \nonumber\]

Entonces, queremos averiguar cuántos átomos están encerrados en la celda cuadrada,\(2 \mathrm{~d}\) unidad. Hay un átomo completo en el medio, y cuatro esquinas que contienen cada una\(1 / 4\) de ellas un átomo.

4\(* \dfrac{1}{4}\) átomos de esquina por átomo\(+1\) central de esquina\(=2\) átomos por celda unitaria

La densidad de empaquetamiento en dos dimensiones es el número de átomos por nm cuadrado. Simplemente podemos dividir el número de átomos en la celda unitaria por el área de la celda unitaria:

\[\text { packing density }=\dfrac{2 \text { atoms per unit cell }}{(3.5 \AA)^2 \text { per unit cell }}\left(\dfrac{100 \AA^2}{1 \mathrm{~nm}^2}\right) \approx 16.33 \text { atoms } / \mathrm{nm}^2 \nonumber\]

La fracción de empaquetamiento en dos dimensiones es la fracción de espacio ocupada por átomos:

\ begin {recopilada}
\ texto {fracción de empaque} =\ frac {\ texto {área ocupada por átomos}} {\ texto {área total}} =2 [\ texto {átomos}/\ texto {celda unitaria}] *\ izquierda (\ frac {\ pi r^2 [\ texto {área por átomo]}} {a^2 [\ texto {área por celda unitaria}]}\ derecha)\\
= frac {2\ pi *\ izquierda (\ frac {\ sqrt {2}} {4 } a\ derecha) ^2} {a^2} =\ frac {\ pi} {4} =0.7854
\ fin {reunidos}