6.14: Índices Miller y espaciado interplanar

Índices Miller

En cristalografía, utilizamos índices Miller para especificar ubicaciones, direcciones y planos en un cristal. Las coordenadas\(\mathrm{x}-\mathrm{y}-\mathrm{z}\) cartesianas estándar utilizan una base que consiste en tres ejes ortogonales en tres dimensiones con longitud unitaria. En la notación de índice Miller, nos basaremos en los vectores de celosía de la celda unitaria como nuestra base. En\(3.091\), ya que estamos trabajando con celosías cúbicas de Bravais, los vectores de celosía cristalográfica son todos ortogonales y de la misma longitud (con la longitud específica de un sólido particular). Con este marco, podemos especificar un punto arbitrario en términos de sus proyecciones sobre los vectores de celosía, al igual que lo harías con las coordenadas cartesianas estándar:

\(\text { location }=h \overrightarrow{a_1}+k \overrightarrow{a_2}+l \overrightarrow{a_3}\)

donde\(\overrightarrow{a_i}\) están los vectores unitarios con cierta magnitud y dirección, y los valores de\(h, k\), y\(l\) especifican hasta dónde ir a lo largo de cada vector de celosía. Podemos expresarlo en taquigrafía como\((h, k, l)\), ¡así como escribirías un par ordenado de coordenadas cartesianas! Una nota rápida sobre la notación: ¡en los índices Miller, los corchetes y las comas importan mucho! Aquí hay una lista rápida de las opciones y lo que significa cada una:

\ (\ begin {array} {c|c}
\ text {Notación} &\ text {Representación}
\\\ hline\ hline (h, k, l) &\ text {punto}\\
{[h k l]} &\ texto {dirección}\
\ langle h k l\ rangle &\ text {familia de direcciones}\\
(h k l) &\ texto {plano}\\
\ {h k l\} &\ texto {familia de planos}
\ end {array}\)

¡Ten en cuenta que solo los puntos usan comas! Por último, los pesos negativos se pueden representar con una barra sobre el número relevante: el desplazamiento en la\(\overrightarrow{a_1}\) dirección negativa estaría indicado por\([\bar{h} k l]\), por ejemplo.

Las direcciones y planos se pueden especificar algorítmicamente:

Direcciones

Una dirección cristalina se define en el contexto de una celda unitaria, y el vector que define la dirección siempre pasa por el origen de la celda unitaria. El vector se extiende desde el origen hasta la ubicación especificada en términos de los vectores de celosía

\(h \overrightarrow{a_1}+k \overrightarrow{a_2}+l \overrightarrow{a_3}\)

donde es nuestro trabajo determinar los valores de\([h k l]\). Para determinar la dirección cristalográfica dada una imagen de un vector en una celda unitaria:

1. Desplazar el vector de tal manera que intersecta el origen de la celda unitaria (si no lo hace ya)
2. Hacer una marca en el borde de la celda unitaria donde el vector se cruza con el marco de celda unitaria
3. Determinar la fracción de cada vector reticular atravesado
4. Multiplica las fracciones por un múltiplo común para producir\(\mathrm{hkl}\) valores enteros que definen la dirección

Por supuesto que también puedes ir por el otro lado, de una dirección\([h k l]\) a un dibujo. Para representar una dirección\([h k l]\) en una celda unitaria:

1. Dividir a través del vector\([h k l]\) por cualquiera de\(h, k\), y\(l\) es el más grande para producir valores fraccionarios
2. Coloque la punta del vector en el punto en el borde de la celda unitaria definida por la fracción encontrada anteriormente
3. Conecte el origen a la punta vectorial

Ejemplo\(\PageIndex{1}\)

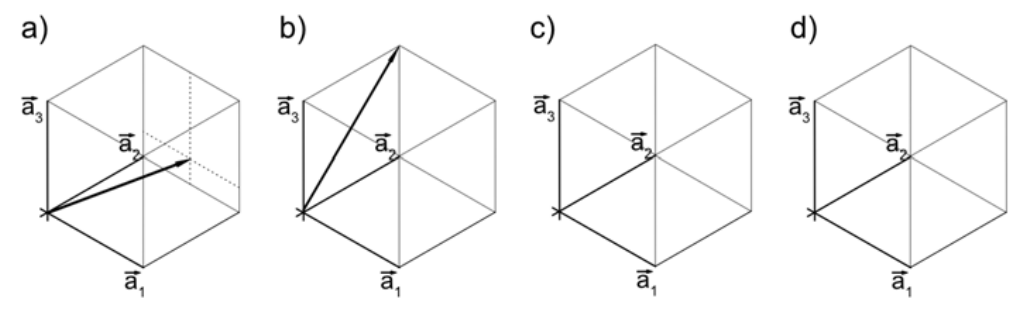
Para a) y b), determinar la dirección cristalográfica indicada en la celda unitaria. Después, para c) y d), esbozar la dirección en los ejes provistos. Para c), boceto [100], y para d), boceto [211].

Solución

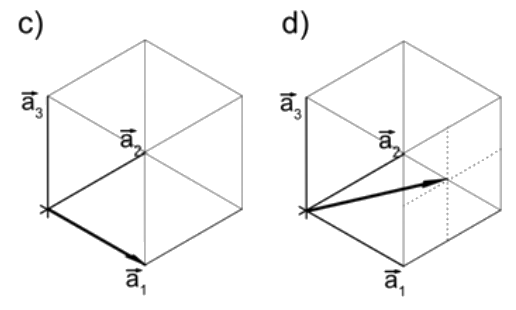
Para a), podemos ver que el extremo del vector se encuentra en\(\frac{1}{2} \overrightarrow{a_1}+1 \overrightarrow{a_2}+\frac{1}{4} a_3\). Podemos convertir esto a una dirección cristalográfica multiplicando por 4 para deshacernos de las fracciones conservando las proporciones. La dirección que se muestra en a) es por lo tanto [241]. Para b), el extremo del vector se localiza en\(1 \overrightarrow{a_2}+1 \overrightarrow{a_3}\), que se representa como [011]. Finalmente, los planos [100] y [211] se muestran a continuación:

Aviones

Similar a una dirección cristalina, generalmente se representa un plano cristalino en una celda unitaria, y se determina en términos de los vectores de celosía\(\overrightarrow{a_1}, \overrightarrow{a_2}\), y\(\overrightarrow{a_3}\). Cuando se le da una imagen de un avión para identificar:

1. Hacer una marca en cada borde de la celda unitaria donde el plano se cruza con el marco de la celda unitaria
2. Determinar la fracción de cada vector reticular atravesado. Si el avión nunca intercepta un vector de celosía, puede notarlo como interceptor en\(\infty\)
3. Tomar el recíproco de cada intercepción fraccionaria\(\left(\frac{1}{\infty}=0\right)\) para producir\(\mathrm{hkl}\) valores enteros que definen el plano

Por último, para esbozar un plano dado\((h k l)\):

1. Encontrar el valor recíproco de\(h, k\), y\(l\left(\frac{1}{0}=\infty\right)\)
2. Marcar los valores fraccionarios asociados con\(h, k\), y\(l\) en los\(\overrightarrow{a_1}, \overrightarrow{a_2}\)\(\overrightarrow{a_3}\) ejes y
3. Conecte las marcas en el borde de la celda unitaria para formar el plano

Ejemplo\(\PageIndex{1}\)

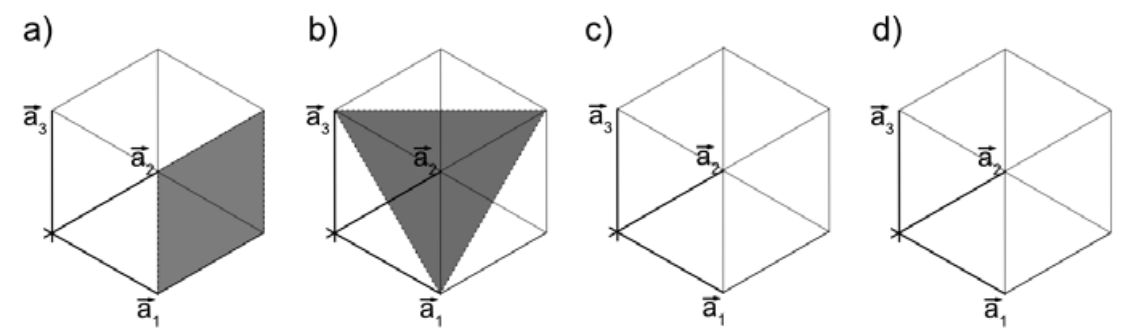
Para a) y b), determinar el plano mostrado en la celda unitaria. Después, para c) y d), esbozar el plano dado en los ejes provistos. Para c), esboce el plano (101). Para d), esboce el plano (001).

Solución

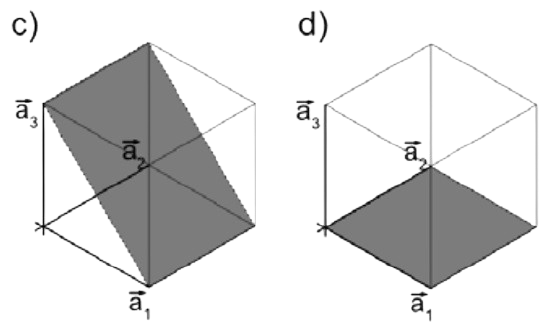
Para a), el plano se cruza\(\overrightarrow{a_1}\) en el borde de la celda unitaria, que es 1. Es totalmente paralelo a\(\overrightarrow{a_2}\) y\(\overrightarrow{a_3}\), así decimos que intercepta en\(\infty\). Tomando los recíprocos de estas intercepciones rinde\(\left(\frac{1}{1} \frac{1}{\infty} \frac{1}{\infty}\right)\), por lo que este debe ser el plano (100). Para b), el plano se cruza\(\overrightarrow{a_1}\) en 1 y\(\overrightarrow{a_3}\) en 1. Si extendemos el plano a lo largo de la\(\overrightarrow{a_2}\) dirección positiva, no intercepta el eje. Pero hay que recordar considerar también la otra mitad del cristal: si tuviéramos que extender el plano hacia atrás, interceptaría\(\overrightarrow{a_2}\) en\(-1\). Tomando reciprocales,\(\left(\frac{1}{1} \frac{1}{1} \frac{1}{1}\right)\) cede el plano (1111). Finalmente, los planos (101) y (001) se muestran a continuación:

Podrías notar que algunas direcciones y planos en el cristal se ven iguales: los átomos están espaciados la misma cantidad. Esto se debe a la simetría en un cristal: por ejemplo, si miras hacia abajo alguna de las diagonales en una celosía cúbica, ¡los átomos que “ves” tienen el mismo aspecto! Estas direcciones y planos equivalentes se llaman familias. Por ejemplo, la\(\langle 100\rangle\) familia de direcciones incluye\([100],[010],[001],[00 \overline{1}],[0 \overline{1} 0]\), y\([00 \overline{1}]\) en un cristal cúbico.

Espaciado interplanar

Para encontrar la distancia entre planos paralelos vecinos, calculamos el espaciamiento interplanar,\(d_{h k l}\).

\[d_{h k l}=\dfrac{a}{\sqrt{h^2+k^2+l^2}} \nonumber\]

Aquí,\(a\) está el parámetro de celosía, generalmente expresado en [nm].